2.1. Mineral processing industry

The mineral processing industry consists of a series of processes that occur in the ore benefaction chain, from the moment raw ore is extracted in situ from ore deposits until the product, at specific grades, is delivered to metallurgy industries. Comminution is an important unit operation of the mineral processing chain that involves rock blasting and mechanical comminution (crushing and grinding). The goal is to liberate the minerals of interest from raw ore so that subsequent concentration processes can operate optimally (Hodouin et al., 2001).

2.2. Quarrying industry

The quarrying industry is fundamental for civilization because its products are used to build roads, buildings, and various types of structures upon which people depend. In 2017, the European Union alone produced 2.86 billion tonnes of aggregates, and Germany (591 million tonnes) and France (463 million tonnes) were the countries that contributed the most (Uepg.eu, 2017). Although most of the comminution from rocks to aggregates and gravel occurs in crushing circuits, very similar to the ones observed in the mineral processing industry, the production goals of aggregate plants are substantially different from these of a crushing circuit in a mining plant (Rylander and Axelsson, 2013). The profit of a quarrying plant is heavily impacted by the product properties (flakiness, shape, strength, and bulk density) (Ruuskanen, 2006).

2.3. The usage of cone crushers

In both the mineral processing and the quarrying industries, cone crushers perform secondary and tertiary crushing tasks, in which the ore diameter is reduced from as large as 250 mm to less than 10 mm. The main differences are that in the quarrying industry, (i) the product of a crushing circuit is the final product (crushed material may be processed further in the mineral processing industry), (ii) the final product has a relatively lower value than the product from the mineral processing industry, and (iii) the final product must meet stringent requirements, concerning both particle shape and particle size distribution (such as the CE marking of aggregates). Thus, the quarrying industry has sought advanced crushing technology and process control strategies to maximize profit (Svensson and Steer, 1990).

On the other hand, in the mineral processing industry, the product of a tertiary crushing circuit typically goes through several more comminution and concentration steps until the valuable mineral is liberated from the raw ore. For this reason, state of the art cone crusher control technology in the mineral processing industry seems to be lagging; the crushing stage is overlooked because it is only a part of a mining plant, and variations in crusher performance are rarely a cause for concern, unless the implications are catastrophic (Bearman and Briggs, 1998). Additionally, the mineral processing industry is mostly concerned with the particle size distribution of the product (Evertsson, 2000); i.e., the product shape is rarely important.

2.4. Overview of the mechanical and operational aspects of cone crushers

Although the cone crusher definitions presented here are limited and superficial, this section provides the reader with the necessary knowledge to understand the decisions made with respect to process variables and control strategies in the publications from the literature. Some discussions, albeit interesting and important for the complete understanding of the physics and mechanics behind operating aspects of cone crushers, are beyond the scope of this paper. The reader is referred to Svensson and Steer (1990) for a discussion about the physics involved in rock crushing inside a cone crusher; Bearman and Briggs, 1998, Lindqvist and Evertsson, 2006 for comprehensive insights into the effect of liner wear and feed properties on the operational characteristics of cone crushers; and Wills and Finch, 2016a, Evertsson, 2000 for a detailed description of the mechanical operating aspects of cone crushers.

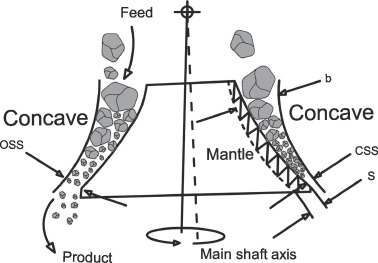
Fig. 1 presents a simplified diagram of a cone crusher. Cone crushers consist of a circular outer concave enclosing a cone-shaped mantle that moves eccentrically, see Fig. 1. As the distance between the mantle and concave inner wall increases, rock particles fall; when the distance decreases, the particles are compressed and crushed.

1. Download : Download high-res image (167KB)
2. Download : Download full-size image

Fig. 1

The minimum distance between the mantle and concave is defined as the closed side setting (CSS) of the cone crusher. The CSS is easily changed online in a large variety of commercial crushers; different principles of CSS adjustment are described in (Quist, 2017). The maximum distance between the mantle and concave, on the other hand, is defined as the open side setting (OSS). The difference between the OSS and CSS is often called the stroke, and it represents the eccentric throw of the mantle (Asbjörnsson et al., 2012). Usually, cone crushers operate at a fixed eccentric speed. It is possible to change this speed online by means of a frequency drive; however, this is not a typical practice in the industry since such equipment is still expensive (Hulthén, 2010). The area indicated as b in Fig. 1 is defined as the bed thickness, and the area indicated as s is equivalent to the difference between the OSS and CSS—the stroke—and represents the eccentric throw of the mantle (Asbjörnsson et al., 2012). The compression ratio is defined as $\frac{s}{b}$. The mantle surface in contact with the rocks is protected by a layer of material called the liner (made of plastic, cement, zinc or epoxy resin (Wills and Finch, 2016a)). The efficiency of a cone crusher varies with the liner wear, and once this wear falls below some acceptable level, worn liners are replaced with new ones as a part of the maintenance routine.

Cone crushers have a safety mechanism, which may consist of springs or hydraulic cylinders, to protect the equipment from extreme operating conditions, such as when the processed material is too hard or some unexpected material enters the crusher chamber. In these situations, depending on the equipment, either the concave (bowl) lifts upwards or the mantle drops so that the uncrushable material can pass without damaging the equipment. Both principles lead to an increased CSS.

The major industrial suppliers of cone crushers include Metso (the GP, HP and MP series), Sandvik (the CS and CH series developed from the Allis Chalmers Hydrocone series), FLSmidth (Raptor®   models), Pegson, Terrex, and Kawasaki. The Metso and Sandvik models are the ones most commonly used in the academic literature.

2.5. Concept definitions

This work uses some concepts to measure, compare, and identify superior and inferior alternatives with regard to process control goals. To avoid misconceptions and arbitrary interpretations, their meanings are rigorously defined here.

• •

  Product quality: In the context of the mineral processing industry, this concept refers to the particle size distribution of the product stream. A sieve greater than 80% of the product stream ($P_{80}$) is a common metric for particle size (Wills and Finch, 2016b). In the quarrying industry, the concept of product quality comprises the product shape, flakiness, particle size distribution (Bengtsson and Evertsson, 2006b), and strength (Bengtsson, 2009). Standard tests, which are essentially specific sieving procedures, are used to characterize the shape and flakiness, and each test has its own index (Bengtsson, 2009).

• •

  Efficiency: In both the quarrying and mineral processing industries, efficiency is defined as the extent to which the process is able to convert energy into products that meet the desired product quality; therefore, when the term ’efficiency’ is used to grade or compare control strategies, it refers to the energy efficiency.

• •

  Performance: In both industries, the performance of the control platform of a crushing circuit is measured with respect to the extent to which the circuit is able to meet some or all of its goals. Different from efficiency, performance can be defined based on the following goals of the crushing circuit: maximizing profit, minimizing energy consumption, minimizing waste, obtaining an acceptable particle size distribution and shape, maximizing capacity (Ma et al., 2016); maximizing product throughput at a given particle size, and guaranteeing supply of a given rate of crushed material to downstream processes (Wills and Finch, 2016a). Additionally, KPIs devised for the manufacturing industry can also be used as performance indicators in the process industry, particularly for crushing circuits (Bhadani et al., 2020).

• •

  Safe operation: In both industries, safe operation is determined by the stabilization of the process while respecting safety margins for operations, equipment, and the workforce (Bouchard et al., 2018).

2.6. Operating variables of cone crushers

It is important to consider the inventory of the available process variables in a crushing circuit to define the control objectives and an overall control strategy. The nomenclature used in this paper is as follows:

• i.

  Operation Parameters. Mechanical design variables are fixed operating parameters that do not change over time, at least without having to stop production. They comprise the stroke, chamber and liner design (including mantle and concave angles).

• ii.

  Disturbances. These variables may change significantly over time, and the process has little to no control over them. They include the particle size distribution and the composition and physical properties of the feed. Disturbances are exogenous signals that affect the process; we know that they exist, but it takes great effort to model and predict their magnitude and frequency. One definition of robustness lies in the ability of a controller to minimize negative effects from the disturbances on the control goals.

• iii.

  Manipulated Variables. These variables change over time during operation, and the operator is able to set their values to some extent. They include the CSS, the eccentric speed, and the choke level. Note that this section considers only the manipulated variables of the cone crusher itself; however, when controlling a crushing circuit, other manipulated variables can be included.

• iv.

  Controlled Variables. These variables are measured or estimated operation variables that may act as a proxy for crushing performance or safety. They include the power draw and chamber pressure. The former is defined in terms of the crusher current (if only an ampere meter is available) and the power factor, and the latter is often measured as the hydraulic pressure, although strain gauges on the cavity are also possible. Moreover, variables such as the product particle size distribution, product shape, and process throughput can be included in this class. This being said, depending on circumstances, the latter could also be considered either a disturbance or a mechanical variable.

The following paragraphs detail the variables mentioned above.

3.1. Population balance models

Population balance models (PBM) of cone crushers must consider how the probabilistic and periodic events of breakage and the creation of smaller particles affect the particle behavior inside the equipment. In the literature, this is addressed by breakage, selection, and classification functions. The following convention is generally adopted:

• •

  The breakage function (sometimes called the appearance function) defines the elements of a lower-triangular matrix that gives the proportion of each size fraction a particle breaks into when a fragmentation event occurs;

• •

  The selection function defines the elements of a diagonal matrix containing the breakage rate of particles by size fraction; and

• •

  The classification function defines a diagonal matrix in which the elements are the probability that particles leave a crushing zone—the whole crusher chamber or a fraction of it—depending on the particle’s size.

Simplifications and variations of the PBM are usual. In fact, the classification matrix in Eq. 1 is a combination of the discharge rate matrix and the selection function. It is only valid at the steady state, assuming that the discharge rate is proportional to the reactor content (Sbárbaro, 2010). Another variation often observed in that the comminution literature is that the selection matrix is used to describe a probability rather than a breakage rate (e.g., Evertsson, 2000, Anticoi et al., 2018). Although both variations make use of matrices, using the breakage probability is sometimes referred to as the matrix approach, while using the breakage rate is occasionally called the kinetic approach (Machado Leite, 1990). The matrix approach is typically accurate when the comminution equipment can be considered fixed residence time equipment.

Sometimes, the selection matrix is a function of the power draw, which is consistent with the classic comminution theory stipulating that decreasing the particle size requires an energy increment to the system (Wills and Finch, 2016b). It is also common practice in the literature to divide the length of the cone crusher into several crushing zones that have their own dynamics; however, their input and output streams are connected, as observed in Herbst and Oblad, 1985, Atta et al., 2014, Evertsson, 2000.

Since the dynamics of wear evolve much slower than the fragmentation, different authors extended the steady-state model of Whiten (1972) to account for wear. Moshgbar et al. (1995) modelled the rate of wear of the concave and the mantle liners and used this information to transform the classification function parameters into time dependent functions. This new information allowed them to investigate an adaptive control strategy in which the CSS value compensates for wear by varying in real time. Andersen and Napier-Munn (1990) also developed liner wear functions but used regression analysis. They modelled the classification function parameters as varying with the CSS, the mass flow rate, the feed size, the liner length, and the expired fraction of the expected liner service life. These approaches are advantageous for studying the wear phenomenon since the computational requirements are low. The results show that the longer the liner is, the greater is the capacity of the cone crusher. On the other hand, the more worn the liner is, the smaller is the capacity of the cone crusher. Therefore, although it is financially attractive to wait as long as possible to change worn liners because of the cost of a new liner, at some point, the production loss caused by wear outweighs the cost of a new liner. To study both fast dynamics (i.e. fragmentation) and wear, one could use the model of Sbárbaro (2010), which is a dynamic equivalent of Eq. (1), and combine it with the wear functions of either Andersen and Napier-Munn (1990) or Moshgbar et al. (1995). Sbárbaro (2010) presented dynamic simulations of a whole comminution circuit, including a crushing circuit, screens, conveyor belts and grinding mills, and studied different process control schemes. These results could possibly be extended by including wear functions.

Although the model of Whiten (1972) showed adequate performance, the premise of the crusher acting as a single mixer and classifier remains questionable. As such, Herbst and Oblad (1985) proposed a dynamic PBM for cone crushers considering the chamber volume as a series of zones. A Kalman filter was used to estimate the particle size in each intermediate zone, power draw, and product feedrate. Arguably, this is a more realistic representation of the dynamics in a cone crusher, but it is difficult to validate because it would require measurements of the particle size distribution of the material inside the crushing chamber at different heights to do so.

Other interesting steady-state representations have been proposed apart from Eq. (1). For instance, Machado Leite (1990) developed a PBM comprising a breakage rate function that assigns particles to be broken to three energy levels depending on their size with the greater particles being broken at a faster rate since they are more likely to contain flaws (cracks). Their representation considers the effect of the CSS in the following two ways: (1) they calibrate the residence time as a function of the CSS, and (2) the selection functions depend on the CSS. Their approach contrasts with the one of Whiten (1972) in which the CSS influences the residence time indirectly through a classification matrix. Moreover, their paper presents an interesting discussion regarding an improved selection function with physical meaning and constraints to facilitate calibration by numerical methods.

An interparticle breakage model was developed in Lee and Evertsson (2008) and validated in full-scale tests in Lee and Evertsson (2011). In the latter, the authors emphasize that significant gains in both product yield and process capacity can be achieved with adequate process control.

A mechanistic modular model for particle flow, size reduction, and pressure prediction in cone crushers was developed in Evertsson, 2000, Evertsson, 1995, Evertsson and Bearman, 1997, Evertsson, 1998, Evertsson, 1999a, Evertsson, 1999b. The authors defined the size reduction by consecutive events, each with its own breakage and selection function. The initial exploration of the basic operation principles of cone crushers was reported in Evertsson, 1995, Evertsson and Bearman, 1997, the breakage characteristics of different materials were investigated and included in the model; the concept of the crusher performance map was introduced in Evertsson, 1998, Evertsson, 1999a, equations of motion that consider the crusher geometry were included to describe the material flow inside the crushing chamber; and Evertsson (1999b) drew additional conclusions on the interaction between material flow and size reduction. The Ph.D. thesis of Evertsson (2000) summarized the findings of the previously mentioned references. The resulting model was validated in full-scale tests. Asbjörnsson et al. (2016) used the mechanistic model described in Evertsson (2000) and the hopper level influence on crushing capacity theory from Sbárbaro (2005) to perform crushing circuit optimization from an operational perspective while considering the effects of wear and plant stops on the production rate. Itävuo, 2009, Itävuo et al., 2013 also used the model from Evertsson (2000) to develop a dynamic cone crusher model, which is discussed in more detail in the next subsection.

Atta et al. (2014), based on the work by Evertsson, 2000, Whiten, 1972, Herbst and Oblad, 1985, proposed a cone crusher model that takes into account several operating characteristics to calculate crusher performance maps and the dynamic response of the crusher. The considered characteristics were classification, selection and breakage, volume capacity limitation, the influence of the eccentric speed in the vertical transport of material, and the influence of mixed materials in the input. Results were obtained for different feed characteristics and for step inputs in the eccentric speed and CSS. The model was extended in Atta et al. (2019) to account for power consumption during the crushing stage using a modified implementation of Kick’s formula. In Atta et al. (2013), a simplified version of the model was used for the process control of cone crushers. A model based on the continuous function method was developed in Johansson (2009) to predict the product size distribution. Karelovic et al. (2015) used Atta et al. (2014)’s cone crusher model in a mixed logical dynamic simulation of a crushing circuit. The resulting model is a hybrid, piecewise affine model that can represent both nonlinearities and discrete events, such as trucks loading run-to-mine ore in a primary crushing station stockpile.

Lindqvist and Evertsson, 2006, Lindqvist and Evertsson, 2003, Lindqvist and Sotkovski, 2003, Lindqvist and Evertsson, 2004, Evertsson and Lindqvist, 2002, also based on the work by Evertsson (2000), modelled linear wear with a mechanistic model. The initial model of the effects on geometry and performance by liner wear was developed in Lindqvist and Evertsson, 2003, Evertsson and Lindqvist, 2002. Some measurement and prediction discrepancies were reported in Lindqvist and Evertsson (2003), and to address these issues, an improved flow and pressure model was presented in Lindqvist and Evertsson (2004). Significant improvements in the prediction of the CSS, power draw and capacity were observed, but only minor improvements in the prediction of wear were observed. In Lindqvist and Evertsson (2006), the effect of shear forces along the crushing surfaces was incorporated into the model, which resulted in significant mitigation of the previously observed discrepancies. The authors emphasized that despite the positive results, the model is still incomplete, as incorrect or incomplete assumptions regarding the operating variables and their relationships might still affect the predictions.

In parallel to the works by Lindqvist on liner wear, Ma et al. (2016) emphasized the importance of an accurate cone crusher model for process optimization and proposed a heuristic model that correlates the material hardness, compression ratio, and particle size distribution with the liner pressure during crushing. Based on this correlation, the effect of liner wear on product quality is estimated and may become an additional tool for the dynamic optimization of the process. The author reported that the liner wear effect leads to significant improvement in the prediction of the particle size and flakiness.

3.2. Empirical models

This section reports on works in which the breakage mechanism is either not modelled, is not modelled with the typical breakage-selection-classification approach, or where the breakage is an empirical function of other variables. We also discuss empirical models derived from the analysis of operating data supported by machine learning tools.

Bengtsson and Evertsson (2006a) developed an empirical model that correlates the average particle size of the feed and the CSS with the product flakiness index, an important variable in the quarrying industry. This work showed some discrepancies with respect to the accuracy of the model, which were attributed to its simplicity. In the same vein, a linear empirical model calibrated by the least squares method (Ruuskanen, 2006) was also unsuccessful.

Eloranta (1995) reported that the crusher stroke and eccentric speed do not have a large influence on the product flakiness, based on a study with a small sample size. Other authors reached different conclusions. Bengtsson and Evertsson (2006a) concluded that including mechanical knowledge such as the chamber geometry, stroke and eccentric speed may improve the flakiness model. Ruuskanen (2006) suggested a structure for a sophisticated model. The particle breakage should be based on the structure of the particle, and the reliability of product shape and liner wear calculations can be increased by considering the mineral contents of the raw ore. In Bengtsson et al. (2009), the product shape model from Bengtsson and Evertsson (2006a) was used to optimize the flowsheet design and operation parameters of a crushing circuit. Bengtsson (2009) reported that the model in Bengtsson and Evertsson (2006a) was extended to accommodate the CSS, feed particle size, throw and eccentric speed. The model was validated in breakage tests using different types of rock. A new model extension considering the interparticle shape for vertical shaft impact crushers was developed in Bengtsson and Evertsson (2006b).

Gang et al., 2009b, Gang et al., 2009a proposed a heuristic model of cone crusher throughput and product flakiness based on the crushing chamber geometry, rotational speed, material harness, and bulk density of the final product. The authors sought a simpler model representation than that of Evertsson (2000). The model was validated using full-scale tests in Gang et al. (2009b). The product particle size distribution and particle shape models were combined to obtain a flakiness prediction model. The optimization of cone crushers was studied while considering the output flow rate as an objective function and the flakiness and particle size models as constraints. Their model was used to optimize the chamber dimensions in Gang et al. (2009a), and a prototype was built to validate the results.

Some modeling attempts from the literature resulted in crushing circuit simulation packages. Itävuo (2009) developed dynamic models with first-order or second-order dynamics plus dead time dynamics based on the static regression models in Ruuskanen (2006) and the particle flow description in Evertsson (2000). The result was a dynamic simulation package of crushing circuits. Later, Itävuo et al. (2013) extended this work to account for the dynamic behavior of cone crushers in the presence of input disturbances. A dynamic model combining the blasting and crushing stages in the quarrying industry was developed in (Csöke et al., 1996). This model considers empirical blasting and the breakage function of cone crushers, along with a probability model of vibrating screens, and is delivered as a computer program for optimization and planning. A toolbox for the dynamic simulation of crushing circuits was developed in Asbjörnsson et al., 2012, Asbjörnsson et al., 2013, Asbjörnsson, 2013, Hulthén et al., 2012b, Hulthén et al., 2012a, Asbjörnsson, 2015. Asbjörnsson et al. (2012) revealed a dynamic mass balance model incorporating a wear function that was developed for a commercial dynamic simulation software called SysCAD. The Swebrec function (Ouchterlony, 2005), which was originally developed to describe the particle size distribution of blasted rock, was used to describe the particle size distribution in the crusher. The results from a previous work (Svedensten and Evertsson, 2005) verified the feasibility and accuracy of the prediction. Asbjörnsson et al. (2013) performed simulations using Simulink to increase the modeling flexibility. The equipment models were differential equations in which the parameters were obtained from fitting real plant data. The Licentiate of Engineering Thesis and the Ph.D. thesis of Asbjörnsson (Asbjörnsson (2013) and Asbjörnsson (2015) respectively) summarize the previous results. Applications of the toolbox for plant performance evaluation (Asbjörnsson et al., 2013) and optimization (Hulthén et al., 2012b) and operator training (Hulthén et al., 2012a) were reported. Based on the crusher model developed by Asbjörnsson et al., 2012, Li et al., 2018 proposed a dynamic model of a SAG mill-pebble crusher circuit.

Methods based on test works to estimate power draw are also worth mentioning due to their frequent applications in commercial simulation platforms. For instance, the JKSimMet software computes the power draw of cone crushers from the estimated particle size distribution and laboratory tests based on the model of Andersen and Napier-Munn (1988) (JKTech, 2015). In a similar manner, USIM PAC first estimates the particle size distribution and then uses this information to estimate the power draw of cone crushers from the Bond Work Index (Caspeo, 2011). Other test work methodologies detailed in Morrell (2019) could likely also be used similarly.

Bearman et al. (1991) performed pilot-plant scale experiments involving a laboratory scale cone crusher to understand and predict the following two operating characteristics: power consumption during the crushing stage; and product particle size distribution as a function of CSS, feed size and rock strength. The authors drew some conclusions regarding the relationship among the operating variables and proposed heuristic prediction models for cone crusher performance and grading curves.

Alvarado et al. (1998) performed economic optimization of a comminution plant (including crushing and grinding circuits) minimizing the energy cost of equipment, using the feed flowrate to the grinding circuit as the single decision variable. The equipment models were based on empirical formulas. Grujić (1996) used empirical equations to model the behavior of the Hydrocone and Symons cone crushers. The parameters were validated using laboratory-scale experiments, and the authors investigated the optimized operation of crushing circuits from both the process control and flowsheet design perspectives.

Most references in the mineral processing literature consider that the processed material is ultimately a commodity, and thus, they are not concerned with the mineral concentration. However, in the case of rare minerals processing, in which the intrinsic value of process material is high, it is important to have such information. The heuristic model developed by Leon et al. (2018) describes the particle size and mineral concentration as a function of the compression ratio and can provide valuable additional information for process optimization.

Itävuo et al., 2017, Itävuo et al., 2014 modelled a crusher feeder-hopper from a combination of mass balance and empirical equations. They used their model to develop an unbiased state observer that guarantees asymptotic convergence. Airikka (2015) used a similar modelling technique that resulted in the implementation of a predictive proportional integrative (PI) controller that manipulates the feeder speed for throughput control. None of the works mentioned in this paragraph developed a crushing model or modelled the breakage behavior but rather provided methods to better understand the mass balance in the crushing circuit.

4.1. Process control of crushing circuits

Process control strategies can be simple (proportional-integrative-derivative (PID) control), complex (plant wide economic model-based control), or any combination in between. Such strategies are among the most reliable ways to improve the operating performance of a process without changing its flowsheet (Garcia et al., 1989, Lotter et al., 2018, Svensson and Steer, 1990). Control strategies seek to optimize some type of performance index or goal (production rate, product quality) by considering a set of operational, financial or environmental constraints (Bhadani et al., 2020). Moreover, process modeling simulation and control also provide a framework for fault detection, operator training, and plant evaluation.

Although many works have contemplated control strategies for grinding circuits, the literature concerning crushing circuits is limited. Since grinding and crushing operate with process-specific equipment, the results observed in the former are not straightforwardly extendable to the latter. Hulthén (2010) argued that the preference for grinding circuits over crushing circuits in the literature is due to the high intrinsic economic value of the products. Liu and Spencer (2004) mentioned that dynamic models of grinding circuit equipment are relatively mature and that researching the appropriate control of problematic units, such as SAG/AG mills, is of interest. On the other hand, the final product of the quarrying industry is usually derived during the crushing stage, and thus, process control of cone crushers is treated with high regard in the quarrying literature. Notably, since some of the performance and product quality goals differ between the mineral processing and quarrying industries, the control strategies adopted by these industries are not directly interchangeable.

The efficient process control of crushing circuits consists of the following two interacting tasks:

• •

  Mass balance control: Adjustment of the level of storage equipment and the delivery dynamics of the raw material (through conveyor belts and tripper cars) to ensure that sufficient feed material is always available for choke-feeding the crusher(s).

• •

  Product quality control: Adjustment of the crusher operating variables to ensure that the product particle size distribution provides a suitable final product or feedrate to downstream processes or that the product quality in terms of shape is adequate.

Neglecting to implement a comprehensive control strategy in crushing plants may lead to low plant performance or unexpected fluctuations due to plant instability (Asbjörnsson, 2013). Moreover, when economic optimization is of interest, simply choosing to maximize one product fraction may lead to the undesirable production of fines (Svedensten and Evertsson, 2005).

Fig. 2 presents a generic representation of a process in a closed-loop with a certain control strategy. Different algorithms may be assigned to the ’controller’ block, such as PID, model predictive control (MPC), and expert systems (ES) (Olivier and Craig, 2017). The basic principle underlying feedback control is the use of plant measurements to reduce the tracking error between outputs and their setpoints. The measurements are either direct measurements of the process output, if available, or some type of estimation via observers or soft sensors. The optimal control actions calculated in the ’controller’ block minimize a cost function that takes into account the previously mentioned tracking error or some other operation goal.

1. Download : Download high-res image (69KB)
2. Download : Download full-size image

Fig. 2

4.2. Control strategies