Parameterless earth fault locator algorithm based on transient surges resulting from single-pole breaker opening

1. Introduction

FAULT event injected traveling wave components in forward and backward directions from the fault point. The generated traveling waves have been exploited in order to identify the fault location. This concept of traveling wave fault location is called passive type as there are not external injected surges. Single-end and Double-end measurements are utilized to implement the passive type of traveling wave fault locations [1].

The potential benefits of applying wavelet transform for analysis of transient signals in power systems have been recognized in the recent years. Ref. [2]presented an improved single end traveling wave fault locating algorithm. A comparison between the discrete and continuous wavelet algorithms on observed data demonstrates that the discrete wavelet transform cannot be adequately applied to a noisy, or heavily filtered signal. As a result, the continuous wavelet transform is presented as the ideal approach to identifying signal reflections. An improved single-ended traveling-wave fault-location algorithm was presented on the basis of experience with conventional substation transducers [3]. The synchronized double-end algorithm is the predominant on overhead transmission lines [4]. It calculates the fault location based on the relative arrival times of the traveling-wave transients at each terminal using a synchronizing clock. The main advantage of double-end algorithm is its function depends on the first arrival surges due to the fault event. In [7], [8], [9], three measuring points are used in order to locate the fault point without utilizing the propagation speed. However, there should be time synchronization between the three measurements.

Single-end measurement cannot help to locate fault point using the passive surges. Accordingly, the active traveling waves are used to locate the fault using single-end measurement. It is implemented by observing the time delay between successive reflections in the traveling-wave signal at one location. An example is the offline approach of time-domain reflectometry used on de-energized cables and transmission lines with the aid of accurate transducers. Although this single-end traveling wave function is simple and its implementation avoids remote-end synchronization, it increases time outage. In order to save time and expanses, there is a motivation behind online active mode fault location and using single-end measurement. In [10], [11], [12], [13], the traveling surges created by re-closure are exploited for locating the faults. In [14], an injected surge was created with the aid of neighbor life network when the faulty network was de-energized. In [15], [16], the zero-sequence surges in unearthed system were injected using a triggered Thyristor in order to identify the faulty feeder. The concept of single-pole auto-reclosure has been adopted by several electricity authorities in Europe to improve the system dynamic stability [17], [18], [19]. An integrated reclosing technique was developed for enhancing transient stability under single pole tripping in [17]. In [18], the authors combine the merits of optimal and adaptive reclosing techniques for transient stability enhancement. The optimal reclosing time is developed for improving transient stability in distribution system in [19]. Several studies are presented considering the single-pole auto-reclosure in [20], [21], [22], [23] for different issues like for directional relays [20], for discrimination between transient and permanent Faults in transmission lines [21], [22], and for negative sequence superimposed pilot protection technique [23]. These studies are not considering the teed transmission lines for single pole auto-reclosure. In real power systems, the increased penetration and development of renewable energy resources such as wind power are noticed. The penetrated wind power is coupled to the grid with common configuration namely teed lines topology [24]. In this line, Ref. [24] presented an adaptive protection scheme for single-line-to-ground fault in teed lines with wind power based on measuring impedance characteristic. In [25], [26], the wavelet transformer is developed for trapped transmission lines. Ref. [27] presented a literature review on the protection schemes and fault location methods that were applied for multi-terminal lines. In [28], the authors developed a technique to locate faults in distribution networks based on optimal coordination of numerical directional overcurrent relays. However, the transients created by the breaker pole tripping have little concentration on their performance evaluation for different power system applications.

In this paper, the auto-reclosure action is exploited in a novel way to locate the fault point using single-end measurements. The transients generated due to single-pole breaker opening are extracted and their time characteristics are localized using the second derivative of aerial mode 1of the voltage. Furthermore, the traveling wave propagation speed can be omitted from the fault location algorithm by using synchronized double-end measurements. The proposed algorithm is evaluated with the Teed transmission lines, which confirms its accuracy.

2. Proposed fault location technique principles

In this paper, one of the modal voltages is utilized in order to implement the proposed traveling wave-based fault location. The modal transformation is in the form as:(1) $[\begin{matrix} v_{o} \\ v_{m 1} \\ v_{m 2} \end{matrix}] = [\begin{matrix} 1 & 1 & 1 \\ 2 & - 1 & - 1 \\ 0 & 1 & - 1 \end{matrix}] [\begin{matrix} v_{a} \\ v_{b} \\ v_{c} \end{matrix}]$ where va, vb and vc are the phase voltages. vo, vm1 and vm2 are the earth mode and aerial modes, respectively. During earth faults, the traveling surges are attained in both aerial mode 1 vm1 and earth mode v0. Unfortunately, propagation speed of the earth mode is not easily estimated. However, the speed of aerial mode 1 is reliable and it is close to light speed for the overhead transmission lines. Accordingly, the proposed algorithm is applied using the aerial mode 1.

The fault location process started from the instant of interrupting the faulty phase current. Then, the effect of reflected surge from the fault point is extracted to find the fault distance. The traveling wave scenario of the proposed fault locator using single-end measurements is as following:

1.
The single-pole of the breaker at the busbar opened to clear the faulty phase. The fault current interruption occurred at the zero current crossing.
2.
Accordingly, a transient surge traveled toward the fault point and reflected to the busbar.
3.
Using the aerial mode 1 voltage of the faulty phase, the arrival effect of the reflected surge could indicate to the fault distance by:

(2)

L_{f} = 0.5 t ν

where Lf is the fault distance and ν is the propagation speed of the aerial mode1. t is the traveling time and it is measured by the time difference between the instant of fault current interruption until the instant of arrival of the reflected surge.

In order to remove the error due to inaccurate propagation speed, there are concepts used to eliminate it from the traveling wave fault location function as addressed in [5], [6], [7], [8]. One of the concepts depended on simultaneously applying the principles of both single-end and multi-end location functions [6]. The other concept was of double-sided measurements used with minimum three measuring points [7], [8], [9].

Therefore, the following section introduces a new concept to locate the fault distance without using the propagation speed is discussed. The idea is that when the breaker pole opens, a surge traveled to the fault point where a part of the surge transmitted toward the other end of the line while the other surge is reflected. By monitoring the reflected surge and transmitted surge, the fault distance can be easily computed without using the propagation speed.

3. Simulated systems

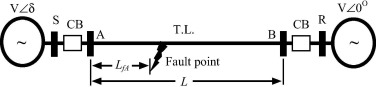
Fig. 1 shows the single line diagram of a 144 km, 400 kV transmission line simulated using ATP Draw software that is utilized as an implementing interface of the ATP/EMTP program [29]. The transmission line is represented using frequency dependent JMarti model. Thevenin’s equivalent impedances at sending and receiving ends (Bus S and R) are described using mutual coupled R-L circuit. The system parameters and transmission line configuration are declared in the Appendix A. In the proposed algorithm, the modal transformation is computed at sending and receiving ends of the transmission line. However, the voltage transducers are to be installed at both line terminals A and B. Accordingly, their voltages can be used to localize traveling surges after breaker pole opening. In this case, the fault distance is estimated based on idea that the reflected surge traveling time is proportional with the fault distance while the transmitted surge traveling time is proportional with the line length as declared in the following example.

The time difference (tB_A − tB.O) indicates to the traveling time over the line while the time difference 0.5 × (tB_B − tB.O) points out the traveling time over the fault distance. Accordingly, the fault distance is computed by,(3) $L_{fB} = 0.5 \times (t_{B_B} - t_{B . O}) / (t_{B_A} - t_{B . O}) \times L$ where L is the line length. The fault distance from side A due to its breaker pole opening is computed by,(4) $L_{fA} = 0.5 \times (t_{A_A} - t_{A . O}) / (t_{A_{B}} - t_{A . O}) \times L$

The algorithm idea is more obvious using the simulated case studies in the following sections.

Fig. 2 shows a Teed transmission system used to evaluate the proposed fault locator. This transmission system is simulated using ATPDraw.

4. Practical evaluation studies

4.1. Evaluation of parameterless traveling wave fault location for UHV transmission system

The proposed algorithm is evaluated for a solidly earth fault case occurred at 1 ms at fault distance 50 km from the sending end S in the system shown in Fig. 1. The sampling rate is considered 1 MHz where the accuracy of traveling wave fault location depends on the sampling rate. For the 1 MHz sampling rate (10−3ms sampling time), the algorithm accuracy by (2) is 0.5 × 10−3 × 294 = 0.147 km = 147 m where the propagation speed of the simulated line is 294 km/ms. This value also indicates the minimum fault distance that the traveling wave fault locator can estimate. In order to reduce this distance the sampling rate can be increased. For example, if the sampling frequency is 10 MHz, the minimum distance becomes 14.7 m. In order to reduce the simulation time, the breaker pole opening instant is defined at 20 ms. Therefore, the breaker pole interrupted the fault current at zero-crossing instants 21.507 ms and 26.642 ms at the receiving and sending ends; respectively as depicted in Fig. 3a. The interrupting current at terminal B was happened before at terminal A. The aerial mode 1 voltages (vm1) at both ends A and B of the line are shown in Fig. 3b. This figure attains the following:

1.
For vm1 at bus B, there is a negative slope started from the instant of interrupting current at 21.506 ms until 22.147 ms when the slope is disturbed by the reflected surge from the fault point. The time difference is tB = 22.147 − 21.507 = 0.64 ms. By substituting in (2), the fault distance from point B is Lf.B = 0.5 × 0.64 × 294 = 94.08 km where the actual fault distance from side B is 94 km.
2.
Similarly, vm1 at bus A, a positive slope started from interrupting instant at 26.642 ms and distorted by the reflected surge at 26.982 ms. Accordingly, the surge traveling time from side A is tA = 26.982–26.642 = 0.34 ms and then the fault distance is Lf.A = 0.5 ∗ 0.34 ∗ 294 = 49.98 km while the actual distance 50 km.

A further simulation fault case related to arcing fault at 50 km distance is implemented in order to confirm the algorithm reliability during arcing faults. Due to arcing fault, the fault period is divided into primary and secondary periods with respect to the breaker status. The primary period is a high fault current strengthening the arcing element while the secondary period is energized from the electromagnetic coupling of the faulted phase by the healthy phases and its starting instant is from the breaker interruption up to the final arc extinction. Considering the arcing fault representation (primary and secondary periods) presented by Kizilcay and Pniok in [30], Fig. 4a shows the faulted phase-a voltage measured at bus A where the arcing fault case is at instant 0.1 s, the breaker at bus A opened approximately at 0.2 s, and breaker at bus B opened approximately at 0.3 s. In other words, the primary arcing period is around from 0.1 to 0.3 s while the secondary arc period is roughly from 0.3 to 0.5 s. However, the primary and the secondary arc currents are power representation, but, nonlinear waveform because the arc element itself is nonlinear over the half-power cycle. Furthermore, the recovery voltage is also power frequency nature. However, the proposed fault location is associated with the transients traveled over the line. Therefore, the important factor is the transient recovery voltage that is mainly coming from the traveling wave transients and exploited to find the fault distance. Using the zoomed waveform shown in Fig. 4b, the fault distance can be estimated that 0.5 × (206.85–206.51) × 294 = 49.98 km, in which the fault at 50 km from bus A.

The above-attained information confirms the fault location is correctly estimated using the transients due to single-pole breaker opening. However, directly extracting the arrival surge time from the aerial mode 1 voltage waveform is difficult. The traveling wave feature extraction has been evaluated using wavelet and recently using Park’s transformation [2], [3], [4]. However, signal processing tools and frame representation have to be implemented. In this paper, the derivatives of the aerial mode 1 voltage are computed in order to extract the arrival time of the reflected surges. The corresponding first and second derivatives are as shown in Fig. 3c and d. In Fig. 3c, as the slopes of aerial mode 1 voltage at bus B and A are constant after the current interruption, there are periods tB and tA with a constant derivative as shown in Fig. 3c. At the arrival of reflected surge, the slope is suddenly changed. Using the second derivative, the time localization is very clear to indicate the periods tB and tA as shown in Fig. 3d. However, what is the threshold value can be used with the second derivative. During steady state, the areal mode 1 waveform is 2 Vp × sin ωtwhere Vp is the peak line voltage and ω is the angular velocity. The second derivative is −2 Vp × ω2 × sin ωt.

For 400 kV, 50 Hz system, the maximum of the second derivative is 2 × (400 × 103 × √2) × (2π × 50)^2 = 1.11 × 1011 V/s2. The threshold is accordingly adjusted as 1013 V/s2. Detecting the starting time is easily implemented by monitoring an interruption instant of the faulty phase current. However, time localization of the reflected surge is important. Simply if the single-pole of the breakers at both ends of the line open with much time difference Δt indicated in Fig. 3a, the challenge is less. Time difference that is greater than one millisecond is enough to avoid transient overlap. This time is computed as the line length is 144 km and accordingly traveling time over the line is 144/294 = 0.49 ms.

For the fault case at 50 km from bus A and as shown in Fig. 3a, the breaker pole at bus B opens before the breaker at bus A. Due to breaker pole at bus B opening at instant tB.O = 21.507 ms, a surge arrived at the other side bus A at instant tB_A = 21.997 ms as depicted in Fig. 5 that is reproduced from Fig. 3d using different zooming time band. The reflected surge from the fault point was arrived at bus B at tB.B = 22.147 ms.

By substituting in (4), the fault distance from Bus B is 94.02 km. In a similar way, the breaker at bus A opened at tA.O = 26.642 ms and accordingly a reflected surge from the fault point arrived at bus A at tA.A = 26.982 ms while a surge arrived at bus B at tA_B = 27.133 ms.

By substituting in the Eqs. (3), (4), the fault distance from bus A is 49.85 km.

4.2. Evaluation for teed transmission system

Traveling wave fault location for teed transmission systems can be accomplished using multi-end measurements that should be synchronized. In this section, the proposed fault locator is evaluated to locate earth faults in teed transmission system.

Considering an earth fault case at 50 km from bus A, the corresponding measurements at bus A are shown in Fig. 6. The single-pole breaker opens at C, then A and B at instants tC.O = 33.101 ms, tA.O = 37.333 ms and tB.O = 39.448 ms as depicted in Fig. 6a. Concerning the single pole breaker opening at bus A as shown at the right hand side in Fig. 6b, the localized time of reflected surge is at tA_A = 37.674 ms. Then, the computed fault distance from bus A is Lf.A = 0.5 × (37.674–37.333) × 294 = 50.127 km. Using the parameterless formula (4) with the localized times synchronized with bus B as shown in the right hand side zoomed figure in Fig. 6b, the fault distance is LfA = 0.5 × (37.674–37.333)/(38.05–37.333) × 210 = 49.937 km where the distance between bus A and B is 210 km and the time at which the surge arrived at bus B due to single-pole breaker opening at Bus A equal 38.05 ms. The same fault distance can be calculated using the synchronized data with bus C where the surge arrived at bus C at tA_C = 37.879 ms and the distance between bus A and C is 160 km. Accordingly, the computed fault distance from side A is 49.872 km (See Fig. 7).

Considering the generated surges due to breaker pole of bus C opening, the corresponding zoomed figure is shown at the left hand side of Fig. 6b. The reflected surge is localized at tC_C = 33.578 ms, accordingly the computed distance is Lf.C = 0.5 × (33.578–33.101) × 294 = 70.11 km that is wrongly indicate to the section length LC = 70 km. The localized surge is the reflected one from the T point in the transmission system that is LC = 70 km as shown in Fig. 2. However, considering the second time tC_C = 33.852 ms that is due to the reflection from the fault point, the distance is Lf.C = 0.5 × (33.852–33.101) × 294 = 110.397 km. If the faulty section is not in the side of the measurements, the second arrival surge is utilized. When the fault occurred at the section AO between bus A and the teed point, the parameterless formula can be applied with the synchronized measurement at bus A not bus B as the fault in the direction of bus A. Anyhow, it is recommended to relay on the fault location results computed from measurements at the bus of the faulty section. For the fault case study that was shown in Fig. 5, the fault location calculation from the measurements at bus A is the main reference to find the fault distance. Also, if the fault occurred at the section BO between bus B and the teed point the formula of parameterless applied with synchronized measurement at bus B not bus A as the fault in the direction of bus B. If the fault is exactly at the T point, all calculated distances at the three buses indicate the fault is at the T point. In other words, no one of the algorithms provides a distance less than its section length.