Timber-concrete composite bridges: Three case studies

1. Introduction

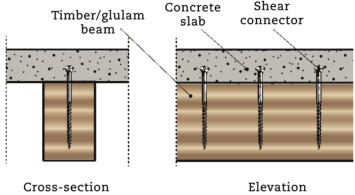
Timber-concrete composite (TCC) beams consist of two parts, an upper concrete slab tied to a lower timber beam by means of shear connectors, as shown in Fig. 1. In the following, a bridge will be defined short if it has a span allowing being designed using standard procedures available in standards and code of practice. The shear connectors resist the shear and induce slab-to-beam composite action – the slab compression resistance complements the beam tensile capacity – so improving the stiffness and strength of the composite beam over those of the beams and slab acting without the connection. TCC beams are stiffer, less prone to vibrations due to the larger damping, and characterized by large shear and flexural strength than timber beams. TCC beams are up to 65% lighter than reinforced concrete (RC) beams as much of the cracked concrete in RC beams is replaced by lighter timber beams in TCC beams, leading to cheaper foundations, faster construction, and lower seismic forces. Since timber has approximately the same strength (in tension and compression) as concrete in compression, it should also be pointed out that timber structures are not bulkier than reinforced concrete structures. Timber is carbon neutral, with far less embodied energy than concrete and steel (glulam joists are only 17%–20% the energy costs of equal steel I-section or RC beams). Thus, timber is popular in sustainable construction and aesthetic appeal, even at cost.

TCC beams have been extensively used to date in Europe both in new and existing buildings (Ceccotti, 1995). In the latter case, better acoustic separation and improved thermal insulation are combined with increased stiffness and greater load-carrying capacity (Berardinucci et al., 2017a, Berardinucci et al., 2017b). Due to the aforementioned advantages, a number of research projects have been undertaken in different parts of the world including Europe (Bathon et al., 2006), North America (Balogh et al., 2008) and Australasia (Yeoh et al., 2009) to investigate applications in medium to long-span building floors.

More recently, applications have also been sought for short span bridge decks in several countries such as Germany (Döhrer and Rautenstrauch, 2006, Kuhlmann and Aldi, 2009), Portugal (Dias et al., 2011), and the United States (Gutkowski et al., 2011). The aforementioned advantages of TCC over all-timber and RC beams, in fact, extend to bridges, where the thin concrete slabs on deeper timber beams visually integrate well into rural landscapes. The concrete slab distributes traffic loads among beams and partly protects the beams from rain (which limits moisture variation in the timber) and wheel impact, so improving durability.

With reference to China, in the last decades, the restriction of the allowable timber materials due to government regulations has limited the number of applications. Recently, timber-concrete bridges and buildings are becoming more attractive and studied (Li et al., 2016). Some tests have been carried out to comprehensively investigate the mechanical behavior (Peng, 2010), and the response of timber-concrete beams have been experimentally compared with timber ones (Chen, 2011). Finally, it is worth noting that some interesting application to bridges in China was recently also realized using bamboo-concrete supporting system (Xiao et al., 2009).

In this paper, the connections commonly employed in TTC short span bridges are reviewed firstly (Section 2). Then, the design procedures adopted for TCC beams are presented with particular reference to Eurocodes (Section 3). The main applications of TCC bridges are discussed and three successful realizations are summarized in detail highlighting the positive aspects (Section 4). Finally, some conclusions and perspectives are drawn (Section 5).

2. Shear connections

In TCC bridges, the mechanical properties of the connections can strongly impact on the stiffness and strength of the composite component. The choice of a structurally effective yet cheap shear connection between the concrete topping and the timber joist is crucial to make TCC structures a viable alternative to more common RC, steel and steel-concrete composite bridges (Berardinucci et al., 2017a, Berardinucci et al., 2017b). Shear connectors should be sufficiently stiff in order to ensure an effective composite action between timber and concrete elements, and several connection systems have been developed to date.

A simple solution is a line of screws, either self-tapping or into pre-drilled holes, vertically placed at a certain spacing along the beam (Fig. 1). Screws have the advantage of being readily available off-the-shelf and easily installed. The recent availability on the market of self-tapping screws with continuous threads has given the opportunity to design a new geometrical configuration where screws are inclined at a certain angle in the vertical plane. Steel rebars and dowels glued to the timber represent one of the first types of connection used for the upgrading of existing floors (Fig. 2). It has the disadvantage of requiring on-site gluing and is generally fairly expensive. Although mechanical connectors such as coach screws, nails, dowels, etc. inserted in the timber without glue are considered to be a simpler way to fasten the concrete slab to the timber beam, they have the disadvantage of being quite flexible and, therefore, requiring a large number of connectors.

On the other hand, using screws inclined at 45° has been proved to result in higher values of stiffness and load-carrying capacities compared to the “traditional” vertical configuration. Several experimental and numerical studies (Bejtka and Blab, 2002; Berardinucci et al., 2017a, Berardinucci et al., 2017b; Blab and Bejtka, 2001; Fragiacomo and Lukaszewska, 2011; Kavaliauskas et al., 2007; Tomasi et al., 2010) have highlighted how the use of inclined screw provides an increase of the resistance and stiffness of the joints, allowing for a reduction of the number of the screws needed in a composite floor under the same geometrical and loading conditions. In addition, an extended model for predicting service and ultimate stiffness and strength of the connections when an interlayer is placed at the concrete-to-timber interface is proposed. In particular, results from pushout tests carried out on specimens consisting of a timber block connected to concrete slabs by means of inclined screws with an interlayer in Oriented Strand Board (OSB) have been presented (Fig. 3, Fig. 4). The OSB interlayer was interposed to reproduce the timber flooring often used as permanent formwork for the placement of the concrete slab in new floors or the existing timber flooring when strengthening existing timber structures.

The use of continuous steel mesh glued to the timber (Fig. 5) represents an alternative connection method to the use of screws and other mechanical fasteners. This technique actually provides an excellent, almost rigid connection. However, it may suffer from high cost due to the gluing process. A cost-effective connection system can be obtained by cutting notches in the timber, which will be subsequently filled in by concrete (Fig. 6). The shear force is transferred by bearing at the timber-concrete vertical interface within the notch. A metal fastener such as a coach screw (Fig. 6), a metal anchor, or a glued rebar is generally used to reinforce the notch and to provide some ductility to an otherwise inherently brittle connection. The main advantage of the notch connection is the high stiffness and strength, which allows for the use of only few connectors to achieve high composite action reducing costs as opposed to mechanical connectors. This is the main reason why the notched connection is the preferred way of fastening the concrete slab to the timber beam, particularly for bridge decks.

3. Design of TCC beams

Unlike steel-concrete composite beams, TCC beams are designed by taking into account the flexibility of the shear connection. The design procedure (Ceccotti, 1995) is based on the approximated elastic solution provided by the Annex B of the Eurocode 5 – Part 1-1 (Comité Européen de Normalisation, 2004) for simply supported composite beams with flexible elastic connections. In particular, the mid-span vertical displacement for a uniformly distributed load g can be evaluated as in Eq. (1).(1)Vmax = 5gl4/(384(EI)ef)where l is the length of the beam and (EI)ef is the effective flexural stiffness of the composite beam given by Eq. (2).(2) ${(EI)}_{ef} = E_{c} I_{c} + E_{w} I_{w} + γ_{c} E_{c} A_{c} {a_{c}}^{2} + E_{w} A_{w} {α_{w}}^{2}$ where E, A and I are the Young's modulus, cross-sectional area, and second moment of area for the single component beam (the subscripts c, w and f refer to concrete, timber and connection, respectively) given by Eqs. (3), (4), (5), (6).(3)γc = 1/(1 + π2EcAcif,ef/(kfl2))(4)if,ef = 0.75if,max + 0.25if,min(5)ac = EwAwH/(γcEcAc + EwAw)(6)αw = γcEcAcH/(γcEcAc + EwAw)where kf is slip modulus of shear connectors, if,max, if,min and if,ef are the maximum, minimum and effective spacing of connectors, respectively, and H is the distance between the centroids of the concrete and the timber cross-sections.

The connector shear force Ff and relative slip sf can be evaluated as in Eqs. (7), (8).(7)Ff(x) = kfsf(x)(8)sf(x) = V(x)γcEcAcacif(x)/(kf(EI)ef)

The concrete axial force and the bending moments can be evaluated as in Eqs. (9), (10).(9)Nc(x) = –Nw(x)(10)Mc(x) = M(x)EcIc/(EI)ef

The timber axial force and the bending moments can be evaluated as in Eqs. (11), (12):(11)Nw (x) = M (x) γwEwAwaw/(EI)ef(12)Mw (x) = M (x) EwIw/(EI)efwhere V and M are the global shear force and bending moment, x is the abscissaalong the beam axis.

The shear strength and slip modulus kf of the connector are determined by testing to failure (pushout tests) small timber-concrete composite blocks.

In addition, the rheological phenomena of the component materials (timber, concrete and the shear connection) should be considered in design as they affect both the stress distribution (ultimate limit state) and the deformation over time (serviceability limit state) (Fragiacomo, 2006, Fragiacomo et al., 2007, Gutkowski et al., 2011, Fragiacomo and Schänzlin, 2013). Concrete, timber and the connection creep over time with different rates, and the creep coefficients of both timber and the connection are also affected by the cycles of moisture content (mechano-sorptive effect) (Toratti, 1992). Concrete shrinkage cannot freely occur due to the connection with the timber beam and therefore causes self-equilibrated stresses (eigen-stresses) and downward deflection of the composite beam. Due to the different thermal expansion coefficients of timber and concrete, a temperature variation of the environment causes eigen-stresses and deformations of the composite beam. Shrinkage or swelling of the timber beam due to moisture content variations related to environmental (relative humidity) variations also leads to eigen-stresses and deformations of the composite beam. More details on the design process of TCC beams, including control of ultimate and serviceability limit states in the long-term, are provided (Ceccotti et al., 2002, Dias et al., 2018).

4. Timber-concrete composite bridges

Timber-concrete bridges are becoming more popular in many countries due to the easy construction and sustainable solution. Even if timber bridges have a very long history, as demonstrated by the ancient ones built in China and other counties, the TCC bridges first appeared in the United States in the early 20th century (Cook, 1976, Richart and Williams, 1943) and the first reported TCC dates back approximately to 1925 (DelDOT, 2000). The USA National Bridge Inventory (NBI) database indicates that over 1000 of this bridge type are still in service after many decades (Wacker et al., 2017). Since the beginning of the 1990s, traffic and pedestrian TCC bridges have been increasingly built and studied in many countries as Finland (Nordic Timber Council, 2002) (Fig. 7), Germany, United States (Ritter, 1990, Weaver et al., 2004), France (Flach and Frenette, 2004), Portugal, Switzerland (Meyer, 2005), Australia (Yttrup and Nolan, 2009), New Zealand, Brazil (Junior, 2008) and also in China (Fu et al., 2014). These bridges have used either rectangular section glulam beams or recycled utility poles.

An interesting TCC bridge was designed by Schaffitzel + Miebach GmbH in 2014 (Fig. 8) in Germany. The shape of the glulam beams follows the bending moment and creates a very harmonic side view. Moreover, the bridge is under monitoring to demonstrate the durability of well-protected timber bridges. The first results of the average timber moisture content, around 16% of mass, indicate that structural protective measures can guarantee acceptable timber moisture contents (Koch et al., 2017). In the following, three TCC bridges will be described in full detail.

4.1. Use of recycled utility poles for short-span TCC bridges

Currently, there is a need for improvement to the transportation system of United States as about 27% of the nation's bridges are deemed structurally or functionally deficient. A possibility investigated at Colorado State University (CSU) consists in the use of reclaimed utility poles for the wood layer of a composite wood-concrete longitudinal deck bridge. As more utility wires are being buried or roadways widened, utility poles that are in good condition are being removed and are available at a very low or no cost. The traditional formworks are only needed on the sides of the bridge deck. Shoring is also unnecessary as the poles provide sufficient support as the concrete layer cures (Gutkowski et al., 2011, LeBorgne, 2007, Miller, 2009).

To overcome the dead load deflection of the beam due to the weight of the concrete and utility poles, it is critical to have camber in the beam since shoring is not practical for bridges. The camber on the underside of the wood-concrete composite beam is natural and comes from the tapered shape of the utility poles and their placement as shown in Fig. 9. To create camber, the tops of the logs are placed level relative to each other so that a natural arching occurs on the underside of the utility poles. However, since the utility poles are different diameters at the ends, the smaller log need to be shimmed so that its top is level with the larger utility pole as shown in Fig. 10.

The interlayer connection is achieved by cutting the notches and reinforcing them with a threaded rod (Fig. 11), which extend all the way through a pre-drilled hole in the utility pole. The rod has a washer on top with a plastic cap (see the red caps in Fig. 12) which protects the washers from the concrete layer once it has been placed. A waterproof paint was applied to the utility poles to keep the swelling of the wood due to the bleeding of the fresh concrete from occurring. After placing the anti-cracking reinforcement (Fig. 12), concrete was placed and left to cure (Fig. 13). 28 days from the concrete placement, the top of the red protective plastic cap was removed and the nut torqued to 34 N·m so as to tighten the rods and reduce the small gaps at the timber-concrete interface due to concrete shrinkage within the notch. Such gaps would significantly reduce the slip modulus of the connection due to the absence of contact between the concrete and the timber within the notch. The nut and the steel plate at the bottom of the rod allow retightening of the rod from underneath the poles, if needed, during the service life of the bridge. It should be noted that only six notches 70 mm deep and 230 mm long were found to be necessary for a 7500 mm span composite bridge. The mean diameter of the poles, which were made of ponderosa pine and douglas fir, was 275 mm, and the depth of the concrete slab above the poles was 170 mm.