Review of fundamental studies on lost circulation and wellbore strengthening

1. Introduction

Wellbore Strengthening, often shortened to WBS, has long been practiced in drilling operations to mitigate lost circulation, even prior to that specific identification. However, studies on fundamental mechanisms of wellbore strengthening became of widespread interest to the drilling industry with the DEA-13 (Drilling Engineers Association - 13) project (Morita et al., 1990). Carefully conducted experimental investigations on lost circulation were conducted, and remarkable enhancements in the pressure-bearing capacity of the wellbore due to wellbore strengthening treatments were observed in the DEA-13 project (Morita et al., 1990, Onyia, 1994). Since then, a number of experimental and modeling studies on lost circulation and wellbore strengthening have been published. It is generally accepted that most lost circulation events are caused by the extension of drilling-induced or natural fractures on the wellbore wall and that wellbore strengthening treatments can effectively mitigate lost circulation by increasing the fracture pressure(gradient) and widening the drilling mud weight window. However, the fundamental physics for the behavior of lost circulation fractures and how wellbore strengthening treatments work are still not fully understood. Different mechanisms and models have been reported in the literature without reaching a consensus (Arlanoglu et al., 2014).

This paper summarizes and organizes fundamental studies on lost circulation and wellbore strengthening published in the literature. State-of-the-art experimental and modeling studies are reviewed. The applicability and limitations of published works are compared and critiqued to clarify challenges and uncertainties encountered and to provide recommendations for future research in this area.

2. A brief background on lost circulation

2.1. Lost circulation and its consequences

Lost circulation (or lost returns) is the loss of partial or whole drilling mud into the formation while drilling a well. The drilling operation may continue when the loss rate is small and partial mud returns can be maintained. However, the operation stops when losses are too large or no mud returns are experienced (Wang, 2007). Lost circulation is a major cause of non-productive time (NPT) in drilling (Cook et al., 2011). Increased non-productive time can substantially increase operational costs, especially in deep-water drilling (Carpenter, 2014).

The mud level in the wellbore annulus may decrease when a large loss occurs. With reduced mud level, the bottom hole pressure may become insufficient to balance fluid pressure from the formation, resulting in the flow of formation fluid into the wellbore, i.e., a fluid kick. As a consequence, well control issues occur. These issues may include underground cross-flow/blowout (formation fluids flow from high-pressure zones to low-pressure or weak zones through the wellbore annulus) and surface blowout (formation fluids flow up to the ground surface) (Wang, 2007). Additionally, wellbore instability (collapse) may take place due to reduced annulus pressure caused by lost circulation. In some cases, the collapsed wellbore may result in buried drilling tools and stuck pipe (Lavrov, 2016, Messenger, 1981).

The above issues caused by lost circulation can significantly increase non-productive time and drilling cost. More than 12% of the non-productive time in shelf drilling in the Gulf of Mexico has been reported due to lost circulation (Wang et al., 2007a). The US Department of Energy reported that, on average, 10–20% of the cost of drilling high-pressure and high-temperature wells in the US is expended on lost circulation problems (Growcock et al., 2009). Worldwide, the impact of lost circulation on well construction is estimated at 2–4 billion dollars annually in lost productive time, lost drilling fluid, and materials used to stem the losses (Cook et al., 2011).

2.2. Lost circulation scenarios

Most mud losses are through hydraulic-driven fractures extending from the wellbore to the far field region (Feng et al., 2016). Lost circulation, therefore, will occur when the mud pressure in the wellbore is high enough to create new fractures or open pre-existing fractures on the wellbore wall. Lost circulation is mostly encountered in formations having a narrow mud weight window, the safe drilling margin between pore pressure (or collapse pressure) and fracture pressure.

Several typical scenarios with a narrow mud weight window are depleted zones, deep-water formations, naturally fractured formations, and deviated wellbores (Feng et al., 2016, Feng, 2016). In depleted zones, pore pressure reduction can lead to a remarkable decrease in the fracture pressure of the wellbore and thus a lower pressure-bearing capacity. In deep-water formations, considerable water depth can cause a lower-than-usual fracture pressure and result in a narrow mud weight window, making it very challenging to maintain needed wellbore pressure. Undesirable wellbore pressure fluctuations due to swab and surge can make things worse. In deviated wellbores, the mud weight window may diminish quickly with an increase in borehole inclination. This may even result in a zero window and an un-drillable well section. Pre-existing fractures in the formation can significantly affect the pressure-bearing capacity of the wellbore. A small fracture can lead to the loss of tensile strength of the wellbore rock and the fracture will propagate when the wellbore pressure overcomes the near-wellbore hoop stress only. If a large fracture is present, the maximum pressure a wellbore can withstand may reduce to the value of the minimum principal in-situ stress or pore pressure (Salehi, 2012).

It should be noted that lost circulation problems are also commonly encountered while drilling through carbonate formations which are often characterized by the presence of vugs and cavities (Davidson et al., 2000, Masi et al., 2011, Wang et al., 2010). However, lost circulation in carbonate formations is outside the scope of this review. The discussion herein is focused on lost circulation resulting from fracture extension in clastic formations such as sandstones and shales.

3. A brief background on wellbore strengthening

3.1. Definition and benefits of wellbore strengthening

Wellbore strengthening can be defined as the approaches used in drilling engineering to artificially increase the maximum pressure a wellbore can withstand without intolerable mud losses. In order words, wellbore strengthening seeks to enhance the effective fracture pressure and widen the mud weight window. Rather than actually increasing the strength of the wellbore rock as the name implies, wellbore strengthening is commonly believed to work by bridging, plugging, or sealing the fractures from which mud losses occur (Feng et al., 2016).

Besides preventing or mitigating lost circulation, wellbore strengthening techniques also have the potential for reducing associated non-productive time events, such as wellbore instability, pipe sticking, underground blowout, and kick. In some situations, wellbore strengthening can help reduce the required number of casing strings, thus reducing well construction costs.

3.2. Preventive and remedial wellbore strengthening

There are two kinds of wellbore strengthening treatments in the drilling industry, namely, preventive and remedial treatments. Simply put, preventive treatments attempt to “strengthen” the wellbore using lost circulation material (LCM) to prevent the creation of new fractures and extension of small pre-existing fractures on the wellbore wall before the lost circulation event. Remedial wellbore strengthening treatments attempt to “strengthen” the wellbore by bridging, plugging, or sealing the lost circulation fractures using LCM after a substantial loss has already occurred.

3.2.1. Preventive treatment

In a preventive wellbore strengthening treatment, LCM has a dual function. First, the LCM accelerates development of a filter cake on the wellbore wall. The filter cake usually has very low permeability and high ductility. It can help maintain a high fracture initiation pressure of the wellbore by effectively inhibiting pore pressure increase in the vicinity of the wellbore (Abousleiman et al., 2007, Tran et al., 2011). Second, the filter cake can quickly seal any pre-existing or drilling-induced micro fractures on the wellbore wall (Aadnøy and Belayneh, 2004, Cook et al., 2016). This prevents fluid flow into the fracture and pressure communication between the wellbore and fracture tip, thus increasing the required pressure for fracture propagation.

Preventive wellbore strengthening treatments based on plastering the wellbore wall with filter cakes have been widely used in the drilling industry and proven to be very effective, especially for lost circulation in depleted sandstone formations with relatively high permeability where filter cakes can form quickly.

Some experimental work reported in the literature has revealed the importance of the filter cake in inhibiting fracture growth and preventing lost circulation (Cook et al., 2016, Salehi et al., 2016, Salehi and Kiran, 2016). Field practices show that adding LCM additives to drilling mud to facilitate the development of filter cake can enhance the effective strength of the wellbore (Song and Rojas, 2006, Soroush et al., 2006, Sweatman et al., 2004). While some researchers insist that wellbore strengthening is achieved by bridging fractures at the wellbore to increase wellbore hoop stress (Alberty and McLean, 2004, Aston et al., 2004, Dupriest, 2005), other researchers maintain that similar wellbore strengthening results can arise by building a low-permeability mudcake on the wellbore wall to alter the effective stresses around the wellbore (Abousleiman et al., 2007, Feng, 2016, Tran et al., 2011).

It should be noted that development of filter cake is a time-dependent process not only because fluid leak-off from the wellbore is a transient process, but also because developments of the thickness and physical properties of the filter cake are functions of time (Bezemer and Havenaar, 1966, Chenevert and Dewan, 2001, Griffith and Osisanya, 1999, Jaffal et al., 2016, Sepehrnoori et al., 2005). These time-dependent processes can significantly affect the stress state around a wellbore (Tran et al., 2011). Properly characterizing the complex, time-dependent features of filter cake remains a challenging problem in the drilling industry.

3.2.2. Remedial treatment

A remedial wellbore strengthening treatment attempts to bridge, plug, or seal the fractures with LCM after drilling fluid loss has already occurred. The ultimate objective of remedial wellbore strengthening treatments is to arrest fracture propagation and increase the maximum pressure that a wellbore can sustain without further significant fluid loss. It is believed that the pressure-bearing capacity of the wellbore can be enhanced by one or a combination of the following mechanisms in a remedial treatment.

•
Bridge a fracture near its mouth to increase the local compressive hoop stress around the wellbore and enhance fracture opening resistance (Alberty and McLean, 2004, Aston et al., 2007, Aston et al., 2004, Bassey et al., 2012, Chellappah et al., 2015, Feng et al., 2015, Loloi et al., 2010, Shen, 2016, Song and Rojas, 2006, Wang et al., 2008, Zhang et al., 2016);
•
Widen and prop a fracture to enhance the fracture closure stress that acts on closing the fracture (Buechler et al., 2015, Duffadar et al., 2013, Dupriest, 2009, Dupriest, 2005, Dupriest et al., 2008, Lai and Woodward, 2014, Montgomery et al., 2007, Vaczi et al., 2009);
•
Form a filter cake in the fracture, especially near the fracture tip, to isolate the fracture tip from wellbore pressure and enhance resistance to fracture propagation (Contreras et al., 2014, Cook et al., 2011, Fuh et al., 2007, Jacobs, 2014, Morita et al., 1996a, Morita et al., 1996b, Morita et al., 1990, Morita and Fuh, 2012, Onyia, 1994, van Oort et al., 2011, van Oort and Razavi, 2014).

Various experimental studies on remedial wellbore strengthening have been reported. Repeated leak-off tests are commonly used to investigate the effectiveness of remedial wellbore strengthening treatments. The fracture pressure for strengthened and un-strengthened wellbore can be evaluated and compared by performing repeated leak-off tests using injection fluids with and without LCM respectively. Both laboratory experiments (Aston et al., 2007, Aston et al., 2004, Guo et al., 2014, Morita et al., 1996a, Onyia, 1994, Savari et al., 2014) and field practices (Alberty and McLean, 2004, Benyeogor et al., 2016, Dupriest, 2005, van Oort et al., 2011) have shown that fracture pressure can be effectively increased by remedial wellbore strengthening treatments. Additional information and discussion on experimental studies are included later in this paper.

Despite successful lab experiments and field applications, the fundamental mechanisms of remedial wellbore strengthening are not thoroughly understood. Much disagreement still exists in the drilling industry. Remedial wellbore strengthening operations are still performed largely on a trial-and-error basis. The industry still lacks adequate mathematic models to quantitatively describe the process. The effects of various parameters, such as the strength and size distribution of LCM, the anisotropy of field stresses, and the location and mechanical behavior of LCM bridge/plugs are still not clear. Studies on these areas are reviewed later in this paper.

It should be noted that both the preventive and remedial wellbore strengthening treatments discussed herein are based on mechanical strengthening of the wellbore, depending on filter cake or bridge development. Alternative wellbore strengthening strategies may include: (1) chemical treatments focusing on changing the chemical composition of the formation (Growcock et al., 2009) or forming chemical sealants in the fracture (Aston et al., 2007), (2) thermal treatments depending on warming up the wellbore to increase its effective fracture gradient (Gil et al., 2006, Gonzalez et al., 2004, Hoxha et al., 2016), and (3) wettability-alteration treatments attempting to change filter cake from oil-wet to water-water to enhance fracture healing when oil-based muds are used (Brege et al., 2010, Quintero et al., 2012). However, these alternative techniques are not included in the discussion of this paper because of the very limited field data available.

In the following sections, fundamental studies on lost circulation and wellbore strengthening published in the literature are reviewed and discussed from four aspects: (1) experimental investigations of wellbore strengthening, (2) physical models for wellbore strengthening, (3) analytical modeling analysis of lost circulation and wellbore strengthening, and (4) numerical simulation studies of lost circulation and wellbore strengthening.

4. Experimental studies of lost circulation and wellbore strengthening

Despite the substantial non-productive time and additional expenditure caused by lost circulation, only a few experimental studies have been conducted on this operationally important topic. Leak-off tests are commonly conducted in experimental studies. Common leak-off test practice is to close the borehole, then increase borehole pressure by injecting fluid until a fracture is created and fluid begins to leak into the formation. Borehole pressure and injection time are usually recorded during the tests. The maximum pressure the borehole can withstand can be read from a pressure versus time curve. By performing repeated leak-off tests with and without LCMs in the injection fluids, the critical pressures for strengthened and un-strengthened wellbore can be compared.

The Drilling Engineers Association-13 (DEA-13) experimental study conducted in the middle 1980's to early 1990's (Fuh et al., 1992, Morita et al., 1996a, Morita et al., 1990, Onyia, 1994) is an early experimental effort on lost circulation and wellbore strengthening. The aim was to explain why lost circulation occurs less frequently while drilling with water-based mud than with oil-based mud and why LCM can help mitigate lost circulation problems. Most of the DEA-13 experiments were conducted on 30×30×30 in. sandstone blocks with a 1.5 in. vertical borehole. Both fracture initiation and propagation pressures were investigated in the experiments because of the relatively large size of the blocks. Two major observations from the DEA-13 project are: (1) fracture initiation pressure (FIP) and fracture reopening pressure (FRP) are almost independent of mud type and the use of LCM additives and (2) formation breakdown pressure (FBP) and fracture propagation pressure (FPP) are strongly related to mud type and substantially increased by use of LCM additives.

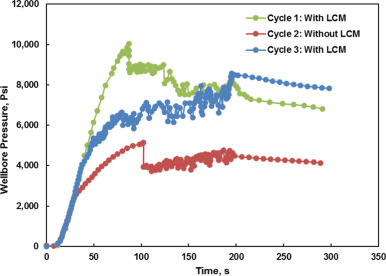
A typical set of DEA-13 experimental data is revisited (Fig. 1) (Onyia, 1994). The maximum and minimum horizontal stresses applied to the block are 2500 and 1800 psi, respectively. A leak-off test with three cycles is conducted. In the first cycle, oil-based mud with 40-lb/bbl LCMs (calcium carbonates) was injected to fracture the borehole until breakdown. A relatively high FBP and FPP is observed. A fracture must have been created after this cycle. In the second injection cycle, oil-based mud without LCM was used to re-fracture the borehole. A much lower FBP and FPP was measured due to loss of tensile strength and removal of LCM. In the third cycle, oil-based mud with LCM was reused to strengthen the borehole. FBP and FPP in this cycle with LCM were about 5000 psi higher than those in the previous cycle without using LCM. As an early effort focusing on resolving lost circulation problems, the DEA-13 experimental study for the first time clearly substantiated that pressure-bearing capacity of a wellbore can be effectively enhanced by wellbore strengthening treatments.

Another experimental effort to investigate lost circulation and wellbore strengthening was the Global Petroleum Research Institute 2000 (GPRI 2000) project conducted in the late 1990's to early 2000's(Dudley et al., 2001; van Oort et al., 2011). Different from the DEA-13 experiments conducted on relative large rock blocks, GPRI 2000 experiments were mostly carried out on 4-in.-diameter cores with 5/8-in.-diameter boreholes. The much smaller sample size allowed only observations of FIP and FRP, but not FPP. The main purpose of GPRI 2000 study was to evaluate the effectiveness of different LCM. It was found that when LCM is added to the mud, FRP was significantly increased. This conclusion is contrary to observations from the DEA-13 study. The experimental results also confirm that LCM is more effective in water-based mud than in oil-based or synthetic based mud. The experimental results suggest that synthetic graphites of specific type and size are preferred LCM candidates.

A third experimental project called Lost Circulation and Wellbore Strengthening Research Cooperative Agreement (RCA), was conducted by M-I SWACO from late 2000's to early 2010's (Guo et al., 2014, Guo et al., 2009). The objective of this project was to investigate wellbore strengthening mechanisms and the effectiveness of various wellbore strengthening methods, including preventive and remedial strengthening methods. Both sandstone and shale blocks of 6×6×6 in. with a 0.1-in.-diameter vertical borehole were used in the tests. The main findings of this experimental study include: (1) a preventive wellbore strengthening treatment can be more effective than a remedial treatment; (2) particle size distribution and concentration of LCM are critical in sealing/bridging the fractures; and (3) fracture pressure achieved with wellbore strengthening treatments can be higher than the breakdown pressure of the intact wellbore, implying wellbore strengthening can not only repair weak formation with induced or natural fractures but also strengthen the formation. A limitation of this experimental study is that the size of the blocks was relatively small. So it was barely possible to observe fracture propagation pressure because the fractures propagated very fast to outside block face after initiation.

A typical test in the RCA project is shown in Fig. 2. The rock sample used in this test was Grinshill sandstone. The maximum and minimum horizontal stresses applied to the block were 800 and 200 psi, respectively. Drilling mud without LCM was first injected to fracture the intact wellbore and a fracture breakdown pressure of 870 psi was achieved. Subsequently, two repeated injection cycles using the same drilling mud without LCM were conducted to test the strength of the wellbore with existing fractures. The breakdown pressure in these two cycles was about 400 psi lower than that of the intact wellbore due to the loss of tensile strength. In a final cycle, drilling mud including 30-lb/bbl graphitic LCM was used to strengthen the wellbore. Fig. 2 shows an enhanced fracture breakdown pressure of about 1700 psi was achieved in this cycle, which is about 800 and 1200 psi higher than the breakdown pressure of the intact wellbore and fractured wellbore, respectively. This example again evidences the effectiveness of wellbore strengthening treatments.

Aston et al. (2004) reported a field leak-off test practice to verify the effectiveness of wellbore strengthening treatments (Fig. 3). The test was conducted at a depth of 3012 ft in a vertical well in the Arkoma basin, USA. A base mud free of LCM was first pumped to fracture the wellbore, and an original breakdown pressure of 1200 psi was observed. After that, the base mud was replaced by a mud containing 80-lb/bbl LCM to strengthen the wellbore. Fig. 3shows that a fracture breakdown pressure of 2050 psi was reached after strengthening the wellbore, which is about 850 psi higher than the original value. This significant increase in fracture breakdown pressure indicates that the fractures can be successfully arrested by LCM.

Recently, Nwaoji (2012) and Contreras Puerto (2014) made an attempt to strengthen the wellbore using drilling fluids containing both nanoparticles and LCM. A maximum increase of 70.31% and 36.39% in breakdown pressure for tests in a permeable media using water-based and oil-based muds containing nanoparticles and LCMs were reported by Nwaoji (2012). However, Nwaoji did not quantify the advantage of adding nanoparticles to LCMs because wellbore strengthening tests using only LCMs (no nanoparticles) were not presented for.

comparison. Contreras Puerto (2014) reported a maximum increase of 65.1% and 29.7% in breakdown pressure in sandstone and shale respectively using traditional LCM (graphite) together with nanoparticles. A strong relationship between mud filtration and wellbore strengthening was observed. Some degree of filtration was found to be beneficial but high filtration impairs wellbore strengthening. Based on microscopy observation of the post-testing fractures, Contreras Puerto (2014) concluded that fracture tip resistance by forming an immobile mass near the fracture tip is the predominant mechanism of wellbore strengthening.

5. Physical models for wellbore strengthening

As mentioned above, different from its literal meaning, wellbore strengthening does not increase the strength of the rock around the wellbore. It is a technique to alter stress distribution in the vicinity of the wellbore and fracture and/or the fluid pressure distribution inside the fracture to increase fracture pressure of a wellbore, i.e. the maximum sustainable pressure of a wellbore without significant fluid loss. Encouraged by field applications and laboratory tests that show fracture pressure can be significantly increased by wellbore strengthening operations, engineers and researchers have made attempts to develop explanatory models for the physical mechanism of wellbore strengthening (Alberty and McLean, 2004, Aston et al., 2007, Aston et al., 2004, Duffadar et al., 2013, Dupriest, 2005, Dupriest et al., 2008, Guo et al., 2014, van Oort et al., 2011, van Oort and Razavi, 2014, Wang et al., 2009 Wang et al., 2007a, Wang et al., 2007b). Currently, there are three major physical models in the drilling industry for explaining why wellbore strengthening treatments can “strengthen” a wellbore.

5.1. Stress cage model

The stress cage model (Alberty and McLean, 2004) is described as bridging small lost circulation fractures near the fracture mouth to create extra hoop stress around the wellbore. Fig. 4 shows the process of stress caging. When a fracture is created on the wellbore wall, LCM particles are forced into the fracture. The largest particles first wedge the fracture mouth area near the wellbore wall. Then, smaller LCM particles plug the spaces between the larger particles and between particles and fracture surfaces, and then seal the fracture mouth. Next, trapped fluid in the fracture filters into the formation through the fracture surfaces and compressive forces are transferred to the LCM bridge at the fracture mouth. Finally, the fracture is bridged near the fracture mouth and results in an increased hoop stress near the bridge location, which makes the fracture more difficult to open.

5.2. Fracture closure stress model

The fracture closure stress model (Dupriest, 2005) is an alternative explanation for wellbore strengthening. The model focuses on increasing fracture closure stress that acts on the fracture plane and keeps the fracture closed. This is achieved by widening the fracture and plugging it with an immobile mass. Fig. 5shows the fracture closure stress model. A fracture on the wellbore wall is first created and widened to increase the compressive stress (i.e. fracture closure stress) in the adjacent rock. The greater the fracture width, the larger the fracture closure stress. Next, LCM particles mixed with mud slurry are forced into the fracture. Liquid leaks off from the slurry to the formation rock. LCM particles consolidate and finally form an immobile mass in the fracture that keeps the fracture open and isolates the fracture tip from wellbore pressure. The immobile mass will keep developing with filtrate loss until the fracture is packed back to the wellbore wall. The increased fracture closure stress and isolation of fracture tip make the fracture more difficult to open and extend.

5.3. Fracture propagation resistance model

The fracture propagation resistance model, initially called the tip screen-out model, was first put forward by Morita et al. (1990) to explain DEA-13 experimental results and further developed by van Oort et al. (2011) for continuously strengthening wellbore during drilling. Different from the two models above, the fracture propagation resistance model does not aim to alter the near wellbore stress to increase hoop stress or fracture closure stress. Instead, it attempts to increase the formation's resistance against fracture propagation. The model assumes that a filter cake can form inside the fracture with fracture propagation and filtrate loss (Fig. 6). The filter cake can seal the fracture tip and prevent pressure communication between the tip and wellbore, therefore the resistance for fracture propagation can be increased. van Oort et al. (2011) argued that fracture initiation and reopen pressure cannot be increased by wellbore strengthening treatments, but rather fracture propagation pressure can be significantly increased.

It should be noted that the three physical models reviewed above only qualitatively explain the mechanisms of wellbore strengthening at a phenomenon-description level. They do not provide a rigorous mathematic model to quantify how much the fracture pressure can be enhanced in wellbore strengthening treatments and how the factors, such as LCM bridging location and in-situ stress, can affect the strengthening results. Engineers and researchers in the drilling industry have been attempting to use analytical models and numerical simulations to quantify fracture behaviors and pressure-bearing capacity of the wellbore for the past two decades. The following two sections summarize and discuss published analytical and numerical studies.

6. Analytical studies of lost circulation and wellbore strengthening

Compared to other drilling problems, e.g. wellbore instability, there are very few analytical studies for lost circulation and wellbore strengthening. Two key elements that researchers have been trying to quantify from analytical studies are the fracture pressure of the wellbore and the geometry of the fracture. The former is critical for determining drilling mud density and the latter is important for LCM design. It is important to consider the near wellbore stress concentration and pressure distribution within the fracture for determining the two elements.

Ito et al. (2001) applied the penny-shaped hydraulic fracture model, developed by Abé et al. (1976) based on linear elastic fracture mechanics, to analyze wellbore strengthening. The model can be used to estimate the increase of fracture pressure after bridging the fracture at different locations and with different in-situ stress anisotropies and pore pressures. However, the model neglects the existence of wellbore, thus it does not take into account near wellbore stress concentrations. Therefore, it can only be used for fractures that extend beyond the well, but not for short fractures. Additionally, the model assumes that the pressure is uniform inside the fracture from the wellbore to the LCM bridge and does not consider pressure drop along the fracture, not realistic for a relatively long fracture. Modeling results indicate that it is possible to reestablish circulation and continue drilling with mud pressure greater than the least principle stress by plugging the fractures with LCM. It is also shown that the potential increase in fracture pressure above the least principle stress is much larger in formations with low pore pressure than those with highly elevated pore pressure. This result implies that wellbore strengthening treatments should be more effective in depleted reservoirs than in high-pressure deep-water formations, two cases of principal interest of lost circulation mitigation in the drilling industry.

Based on a dimensional analysis and superposition principle with linear elastic fracture mechanics, Guo et al. (2011) developed an approximate, closed-form solution for the fracture mouth opening displacement of two fractures located symmetrically at a wellbore. The model considers the near-wellbore stress concentration. However, the fracture surfaces are still assumed subjected to uniform wellbore pressure or pore pressure. The model is only used to determine fracture opening before applying wellbore strengthening treatments. It cannot provide information about fracture pressure and fracture geometryafter applying strengthening treatments. A comparison with numerical simulation results shows that the model is only valid for a relative short fracture with a length less than 4 wellbore radii and for a maximum to minimum horizontal stress ratio less than 2.

Shahri et al. (2014) proposed a semi-analytical solution for wellbore strengthening analysis based on linear elastic fracture mechanics using techniques of the singular integral formulation of stress field and Gauss-Chebyshev polynomials. The model considers far field stress anisotropy and near wellbore stress perturbation. It can provide fracture width distribution and fracture pressure before and after bridging a fracture. However, the model also does not take into account pressure drop along the fracture. It is assumed that the fluid pressure is equal to wellbore pressure from the wellbore to the LCM bridge and equal to pore pressure from the LCM bridge to the fracture tip. Thus the model is more suitable for short fractures, where pressure drop along the fracture may be ignored. Another limitation of the model is that it does not give a closed-form solution.

Using linear elastic fracture mechanics and the superposition principle, Morita and Fuh (2012) proposed two sets of closed-form solutions for determining wellbore fracture pressure after bridging the fracture at the fracture mouth and away from it. They also assumed uniform pressure distribution ahead and behind of the LCM bridge. The model neglects the influence of the wellbore on the stress intensity factor induced by the fluid pressure from the LCM bridge to the fracture tip. Thus the model is only valid for long fractures for which it is reasonable to ignore wellbore effects. Based on a parametric analysis using the proposed model, Morita and Fuh (2012) concluded that wellbore strengthening methods are effective for stabilizing both micro-fractures (0.1 – 1 in.) and macro- fractures (1 in – 2 ft), and the major parameters affect the magnitude of strengthening are the width and concentration of the LCM materials, Young's modulus of the formation, wellbore size, and in-situ stresses.

van Oort and Razavi (2014) extended the KGD hydraulic fracture model (Geertsma and De Klerk, 1969, Linkov, 2013, Zheltov, 1955) to analyze wellbore strengthening. Solutions for fracture pressure and fracture width after sealing the fracture were derived, but the model neglects both the existence of the wellbore (i.e. near wellbore stress concentration) and pressure drop along the fracture.

Feng and Gray (2016a) presented an alternative wellbore strengthening model by combining Kirsch equations for evaluating near wellbore stresses and a linear-elastic fracture criterion for evaluating fracture stability. The model can be used to predict fracture pressure before and after bridging a fracture. The model assumes two short fractures extending symmetrically from the wellbore wall and perpendicular to the minimum horizontal stress. Given the small length of the fractures, the pressure inside the fracture is assumed to be uniform and equal to the wellbore pressure during drilling. After bridging, the pressure from the fracture mouth to the bridge is equal to wellbore pressure and the pressure behind the bridge is equal to formation pore pressure. Effects of wellbore and fracture geometry, in-situ stress anisotropy, and LCM bridge location are considered in the model. A parametric study by the authors show that the wellbore can be effectively strengthened by bridging the lost circulation fractures, but the magnitude of the strengthening is affected by LCM bridge location, in-situ stress anisotropy, and formation pore pressure (Fig. 7). Fig. 7 shows that the closer the bridging location to the fracture mouth, the better strengthening can be achieved. This means for better application of wellbore strengthening techniques, it is important to accurately predict fracture geometry, especially fracture mouth opening, for selecting the best LCM size. Higher in-situ stress anisotropy results in relatively lower fracture pressure. The results also imply that the wellbore strengthening applications by bridging fractures are more effective for formations with small in-situ stress anisotropy than those with large stress anisotropy (Fig. 7a). Fig. 7b shows that wellbore strengthening is more effective for formations with low pore pressure and in-situ stress ratios, such as pressure depleted reservoirs, as compared to formations with large pore pressure and in-situ stress ratio, such as deep-water high-pressure formations. A limitation of the model is that it assumes short fractures at the wellbore do not significantly alter near wellbore stress concentrations obtained from an ideal Kirsch stress state. Therefore, the model is only suitable for wellbores with short fractures.

Table 1 summarizes published analytical models on lost circulation and wellbore strengthening. It should be noted that all of the models have the following limitations.

•
All the models are based on linear elastic fracture mechanics, so poro-elastic or plastic behavior of the materials cannot be considered.
•
All the models assume stationary fractures with a fixed length, usually 6 in.. The dynamic propagation of lost circulation fractures is not explicitly modeled.
•
The fluid pressure inside the fracture is assumed to be uniform. Fluid flow within the fracture and leak-off into the formation are not explicitly modeled.
•
The LCM bridge is assumed to be a “perfect” bridge with infinite strength and zero permeability. So it completely separates fluid communication between the two sides of the bridge.
•
The bridge location is predefined. The transportation, aggregation, and consolidation of LCMs within the fracture are not explicitly modeled.

Table 1. Summary of the analytical wellbore strengthening models.

Models	Outputs	Theory	Limitations
Ito et al. (2001)	Fracture Pressure	Penny-shape Model	No wellbore, uniform pressure in frac, perfect bridge
Guo et al. (2011)	Fracture Width	LEFM	Uniform pressure in frac, no bridge, short fracture, low in-situ stress ratio
Morita et al., 2012	Fracture Pressure	LEFM	Uniform pressure in frac, partially ignoring wellbore effect, perfect bridge
Shahri et al. (2014)	Frac. Width Frac. Pressure	LEFM	Uniform pressure in frac, perfect bridge, no closed-form solution
van Oort et al., 2014	Frac. Width Frac. Pressure	KGD Model	No wellbore, uniform pressure in frac, perfect bridge
Feng and Gray (2016)	Frac. Pressure	LEFM	Uniform pressure in frac, perfect bridge, short fracture

7. Numerical studies of lost circulation and wellbore strengthening

Since analytical models usually involve many assumptions, they cannot satisfy operational needs for wellbore strengthening analysis, especially for accurately describing fracture behavior and stress evolution during the process. For better predictions, numerical methods are, therefore, applied to simulate the problem and provide valuable implications for field applications. However, compared with numerous numerical studies on wellbore stability and hydraulic fracturingproblems, only a few numerical studies have been published on lost circulation and wellbore strengthening.

Alberty and McLean (2004) employed a 2D finite-element model to investigate fracture geometry and hoop stress in stress caging treatments. The result shows that there exists a hoop stress increase area near the location of the bridge as shown in Fig. 8, and the fracture length decreases after bridging the fracture. The model successfully proves the hypothesis of hoop stress enhancement in the stress cage concept. However, it possesses some limitations, including linear elastic material assumption, perfect bridge, nearly isotropic in-situ stress, no consideration of pore pressure and fluid flow, and predefined stationary fracture.