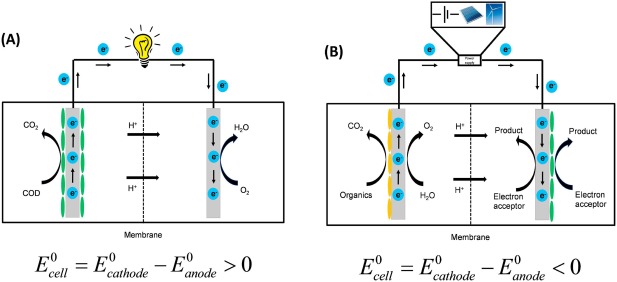
Towards automated design of bioelectrochemical systems: A comprehensive review of mathematical models

1. Introduction

Bioelectrochemical systems (BESs) which use microorganisms to facilitate oxidation/reduction processes through the release/capture of electrons from an electrode have drawn increasing attention in recent years as an emerging technology [1]. A BES like any other electrochemical cell (e.g. battery) also includes an anode, cathode and a separating membrane (optional), but the difference lies in how the electrochemical reaction is catalysed. In BES, at least one or both of the electrode reactions are catalysed with the help of microorganisms. By combining living biological systems with electrochemistry, BES can be used for a plethora of applications such as electricity generation (microbial fuel cell, MFC), hydrogen production (microbial electrolysis cells, MEC), synthesis of value-added chemicals (microbial electrosynthesis, MES), desalination (microbial desalination cell, MDC), and removing contaminants (microbial remediation cell, MRC) [2], [3]. The type of bacterial population, electrodes and substrates used at the anode and cathode and many other biological and design parameters determine the total cell potential ( $E_{cell}$ ) of BES, which if positive ( $E_{cell} > 0$ ), the BES can be used to generate electricity and when negative ( $E_{cell} < 0$ ), additional external power may be required to reduce the electron acceptor at the cathode [1], [4]. These two scenarios are described in the schematic of BES as shown in Fig. 1. While Fig. 1A represents the schematic for a standard microbial fuel cell (the total cell potential is positive), Fig. 1B represents a more general schematic for other BESs. Depending on the particular application, either anode or cathode or both can be biocatalysed and the electron acceptor and product would vary based on the application. The power required in BES when $E_{cell} < 0$ , can also be supplied from renewable energy sources (solar, wind, etc.). At present, renewable electricity from solar photovoltaics and wind-turbines has become readily available, but due to the seasonal nature of sun and winds, these sources do not harmonize well with the market demand and need storage during the off hours. BES offers a perfect technological solution by making it possible to store the electrical energy from renewable sources [4], [5].

BES are complex devices, affected by a number of biological, physical-chemical and electrochemical factors that are dynamically related to each other [6], [7], [8]. The performance of any type of BES depends on a number of parameters such as the type of microorganisms and feed (wastewater), membrane or separator characteristics, voltage or current supplied, mixing and diffusion phenomena, surface area of electrodes, etc. Fig. 2 shows some of most important operational, design and biological parameters that determine BES characteristics. Performance improvement of BES is still challenging and thorough understanding of the relationships among the various parameters and their dynamic processes is important to make this technology more efficient [9].

A number of experimental studies have been conducted to investigate the effect of operational parameters on BES performance [10], [11], [12], [13], [14], [15]. These have helped in improving the BES performance in terms of net electricity/ product generation and scalability, but it is still much lower than that obtained from conventional technologies for similar applications [16], [17], [18], [7]. Furthermore, the detailed understanding of the mechanisms governing the different processes in a BES device from a physical, chemical and biological perspective is still very patchy. Working of BES involves complex interplay between biological and electrochemical processes and thus the development of mathematical models is critical to the design and optimization of these systems in future [18], [6], [9], [19]. However compared to the experimental studies, the number of mathematical models of BES is very limited. Also, within the relatively small number of numerical studies, most research is dedicated to microbial fuel cell (MFC) modeling and very limited work on other BES systems [9], [19], [20]. Some of the previous review articles have outlined the developments in the BES models. For example, Oliveira et al. [6] presented a very comprehensive review of all the developments in mathematical models of MFC. They highlighted the influence of several important parameters on the MFC performance and outlined the progress made on scaling up of BES cells. They also identified the various limitations that result in the suboptimal power output levels obtained from MFCs. Similarly Ortiz-Martínez et al. [9] reviewed and classified the prominent mathematical models describing MFC. They also outlined the advantages and shortcomings of the different modelling approaches including those based on optimization techniques. [18] presented a much broader review of BES modelling efforts including models developed on both engineering and statistical approaches. They also presented the strengths and weaknesses of using the two approaches and how these may influence BES optimization. Recio-Garrido et al. [19] presented an extensive review of the dynamic models of MFC and MEC, along with the studies on BES optimization and control. They point out that mathematical models that account for the biofilm growth dynamics of mixed population of microbes can be most useful in BES system optimization. They also suggest on-line monitoring and development of software sensors can provide better control and real-time performance update of important parameters which would be crucial in obtaining a stable system performance. Recently Xia et al. [20] presented a detailed review on different MFC models, classifying them into mechanism-based and application-based models. While describing the two types of models, they presented the underlying methodologies and usability of the different approaches based on the required output.

As can be seen, most of the previous review articles are largely focused on MFC models. In the last 2–3 years, several new mathematical approaches have been developed for MFC as well as for other bioelectrochemical systems, such as MEC, MES and MDC [8], [21], [22], [23], [24]. In addition, novel mathematical strategies using unconventional methodologies such as the artificial intelligence methods or the cellular network models have also been developed [25], [26]. These mathematical models have to be comparatively and comprehensively analyzed for applicability and future research thrust that this review aims to meet.

2. Classification of models

The mathematical models developed for BES can be classified using many different factors. For example, on the basis of the mode of extracellular electron transfer (EET) used in the models, which can be either mediated or direct; or on the basis of the microbial population considered in the models, either a pure culture with single species or a mixed culture with multiple species, and so on and so forth. These different factors are described in Table 1.

Table 1. Important factors considered in BES mathematical models.

Criterion	Options
Spatial Dimension	1D	2D	3D
Chamber	Anode	Cathode	Both anode and cathode
EET	Direct (conductive biofilm)	Mediated
Microbial Community	Pure Culture	Mixed Culture
Biofilm	No	Yes (biomass attached and/or suspended)

Other than these factors, the models can also be broadly classified based on their mathematical formulation. For example some models are based on ordinary differential equations (ODEs) considering only time dependence and no spatial dimension or steady state models considering only one spatial dimension. Such a simple formulation based on ODEs helps in solving these models faster at a relatively low computational expense. On the other hand, some models have been formulated using a combination of partial differential equations (PDEs) and ODEs considering both time and spatial dimensions or steady state models with more than one spatial dimension. Such models are typically more comprehensive and provide detailed insights into the system. However the additional complexity also makes them computationally expensive and time consuming.

3. Description of models

Table 2 presents a brief overview of the critical factors considered in some of the important BES models. One of the first mathematical model developed for a BES is the model proposed by Zhang and Halme [27] for an MFC. In this relatively simple model, which is based on ordinary differential equations, the biological processes including the substrate consumption by the bacteria and the redox reaction between the metabolites and mediator HNQ (2-hydroxy-l, 4-naphtboquinone) and the electrode redox reaction are modelled using the Monod equation and first order reactions respectively. Citing that $H^{+}$ ions permeation from anode to cathode and diffusion from air to the surface of cathode electrode are very fast, all mass transport processes are assumed to be non-limiting compared to the biochemical and redox reactions [27]. Nernst equation and Faraday’s law is used to calculate the electromotive force and the current respectively. The parameters of the model are first estimated from experimental results by using the least square and trial and error methods and the model is then used for predicting the current output based on the input concentrations of the substrate and the mediator. A correlation between the total over-voltage and current output is also obtained [27]. This model creates a simple formulation based on a lot of assumptions but serves as a good starting point for MFC analysis and acts as a basis for the more advanced models that were developed later.

Table 2. Important BES models and their features.

Empty Cell	Study	Description	EET	Microbial community	Biofilm	Chamber(s)	Spatial Dimension
1	Zhang and Halme [27]	First MFC model	Mediated	Single species	No	Anode	0D (only time dependence)
2	Marcus et al. [28]	First MFC model with conductive biofilm approach	Direct (conductive biofilm)	Two Species	Yes	Anode	1D
3	Picioreanu et al. [29]	Multidimensional computational model for MFCs based on redox mediators	Mediated	Multiple species	Yes	Anode	1D, 2D, 3D
4	Picioreanu et al. [30]	Extension of Picioreanu et al. [29] to Integrate IWA’s ADM1 model	Mediated	Multiple species	Yes	Anode	2D, 3D
5	Pinto et al. [31]	Two-population MFC model based on ODEs	Mediated(intracellular)	Two species	Yes	Anode	0D (only time dependence)
6	Picioreanu et al. [32]	Extension of Picioreanu et al. [29] in order to include pH calculations.	Mediated species	Multiple species	Yes	Anode	2D, 3D
7	Picioreanu et al. [33]	ODE based simple MFC model with suspended biomass and added electron-transfer mediator	Mediated	Single species	No	Anode	0D (only time dependence)
8	Zeng et al. [34]	First two chamber model for MFC	Direct	Single species	No	Anode and Cathode	0D (only time dependence)
9	Pinto et al. [35]	Extension of Pinto et al. [31] to model $H_{2}$ production in MEC	Mediated (intracellular)	Multiple species	Yes	Anode	0D (only time dependence)
10	Merkey and Chopp [36]	2D MFC model with conductive biofilm approach	Direct (conductive biofilm)	Two Species	Yes	Anode	2D
11	Oliveira et al. [37]	Steady state model for MFC accounting for coupled heat, charge and mass transfer	Direct	Single species	Yes	Anode and Cathode	1D (Steady state, only zdependence)
12	Ping et al. [24]	First mathematical model to simulate dynamic behavior of MDCs	Mediated (intracellular)	Two species	Yes	Anode	OD (only time dependence)
13	Sirinutsomboon [38]	Membraneless single-chamber MFC model	Direct	Single	Yes	Anode and Cathode	1D
14	Alavijeh et al. [22]	Generalized model for microbial electrochemical cells	Direct (conductive biofilm)	Two Species	Yes	Anode	1D
15	Kazemi et al. [23]	First MES model, biocathode of BES using conductive biofilm approach	Direct (conductive biofilm)	Two Species	Yes	Cathode	1D
16	Yao et al. [39]	Two-dimensional, two-phase mass transport model	Direct	Single	Yes	Anode and Cathode	2D
17	Recio-Garrido et al. [40]	Combined bioelectrochemical-electrical model	Mediated (intracellular)	Two species	Yes	Anode	OD (only time dependence)
18	Ping et al. [41]	Extension of Ping et al. [24] to model Boron removal in MDC and MFC	Mediated (intracellular)	Two species	Yes	Anode	OD (only time dependence)
19	Esfandyari et al. [42]	Two chamber batch MFC model	Direct (conductive biofilm)	Two Species	Yes	Anode and Cathode	OD (only time dependence)
20	Esfandyari et al. [43]	Two chamber continuous MFC model	Direct (conductive biofilm)	Two Species	Yes	Anode and Cathode	OD (only time dependence)

Picioreanu et al. [29] developed a more comprehensive multidimensional mathematical model for the anodic chamber of MFCs considering a mixed culture of bacteria suspended in the anode chamber and also attached to the anode electrode. Electron transfer from the microorganisms to the electrode is assumed to occur via a diffusible redox mediator. Butler-Volmer equation is used to derive the current density produced in the electrochemical mediator oxidation and ohm’s law is used to calculate voltage considering activation, ohmic and concentration over-potentials. A double Monod kinetic equation is used to calculate the rate of substrate conversion with oxidized mediator leading to microbial growth [29]. Rate of microbial growth resulting from substrate conversion with oxidized mediator is expressed using a double Monod kinetic expression. The bulk of the anode chamber is considered to be ideally mixed and thus the substrate and the biomass concentrations in the bulk do not change in space dimension. However as the substrate is consumed its concentrations changes as a function time based on rates of exchange with the exterior and the rates of reactions in the bulk, in the biofilm and on the electrode. Similarly a mass balance expression is derived for all biomass types depending on the rates of detachment and attachment. Unlike in the bulk, biomass and substrate concentrations change both spatially and with time in the biofilm subdomain depending on the diffusion coefficients and the respective rates of production and consumption. Migration of ions in the electric field is however neglected. Picioreanu et al. [29] used the model to understand the influence of different operational conditions such as substrate utilization yields, standard potential of the redox mediator, ratio of suspended to biofilm cells, initial substrate and mediator concentrations, mediator diffusivity, mass transfer boundary layer, external load resistance, endogenous metabolism, etc., on evolution of important parameters such as current, charge, power, substrate consumption and biomass growth rate. They also identified that current distribution was more uniform in homogeneous biofilms as compared to more distributed spread-out biofilms [29]. Fig. 3 shows the prediction of current density and 2D concentration distributions for the oxidized mediator obtained by Picioreanu et al. [29]. It should also be noted that while 1D and 2D cases using this model can be solved quite easily in a short period of time, solving the full 3D model takes long computational times (14 h for 15 days of MFC operation). Also, though Picioreanu et al. [29]’s model is more comprehensive than Zhang and Halme [27]’s initial attempt, it was only applied for the case of a simple substrate feed (only acetate).

In a later study, Picioreanu et al. [30] extended their previous model [29] by integrating with the IWA Anaerobic Digestion Model No. 1 (ADM1), which allowed the understanding of the interactions between coexisting methanogenic communities and electroactive bacteria transferring electrons to a microbial fuel cell anode via soluble redox mediators. Successively, the original model was further extended by Picioreanu et al. [32] to calculate spatial pH distribution and solutes speciation by adding the Nernst-Planck fluxes of ions (electromigration and diffusion) together with an ionic charge balance. This model also allowed the study of the different two- or three-dimensional geometry of the electrode/biofilm which was an improvement over previous model that only allowed the planar electrode system [32]. Three cases studies were shown to highlight the new features of the model, however the results were not compared with any experimental data [32].

In addition to the above three comprehensive multi-dimensional models [29], [30], [32], Picioreanu et al. [33] also developed a simple mathematical model based on ODEs that accurately describes the dynamics in an MFC anodic chamber with suspended cells and electron transfer via a diffusible mediator. In this model, all variables are considered spatially uniform and just a time dependent solution is presented [33]. This model does not consider any biofilm but includes two domains in the anode chamber, bulk liquid and the mass transfer boundary layer adjacent to the anode. The rate of substrate consumption is derived based on the double Monod expression for the substrate and oxidized mediator concentrations. Current density is expressed using the Butler-Volmer equation and the voltage is calculated using Ohm’s law considering the ohmic and activation over-potentials. Mass balances are formulated for the three soluble components (glucose, oxidized mediator and reduced mediator) in the bulk liquid and in the boundary layer [33]. The kinetic and mass transfer parameters in the model are derived using a parametric estimation study by comparing with experimental data from Delaney et al. [44]. The model has been used to investigate the effect of different operational parameters on the MFC performance [33].

Tables 3A, B, and C present an overview of some of the key equations used in BES models.

Table 3. Commonly used equations in the BES models.

Equation	Description	Reference
A: Equations for Microbial kinetics
Monod kinetics	Model to describe microbial growth rate and substrate consumption rate, when growth rate is only limited by the substrate (nutrient) concentration. $μ$  = specific growth rate, $μ_{\max}$  = maximum specific growth rate, S = limiting substrate concentration, $K_{s}$  = half saturation (Monod) constant, q = substrate consumption rate, $q_{\max}$  = maximum substrate consumption rate.	[21], [31]
$μ = μ_{\max} \frac{S}{K_{s} + S}$
$q = q_{\max} \frac{S}{K_{s} + S}$
Multiplicative Monod Kinetics	Here microbial growth rate is assumed to be limited by concentrations of substrate and oxidized form of the mediator. $K_{m}$  = mediator half saturation coefficient, $M_{ox}$  = oxidized mediator concentration.	[29]
$q = q_{\max} \frac{S}{K_{s} + S} \frac{M_{ox}}{K_{m} + M_{ox}}$
Nernst-Monod Kinetics	Assuming the biofilm as a porous conductive matrix, Marcus et al. [28] derived this equation by combining the Nernst model typically used by electrochemists to describe redox potential with the Monod kinetics. F = Faraday constant, $η$  = local potential, R = ideal gas constant, T = temperature.	[28]
$q = q_{\max} (\frac{S}{K_{s} + S}) (\frac{1}{1 + \exp [- F η / RT]})$

B: Material balance equations
Space independent equations	Substrate and biomass material balance is described assuming biofilm retention with equal influx and effluent rates. This specific model considers that substrate is being consumed by two competing bacterial populations [31]. Subscripts a and m refer to anodophilic and methanogenic bacteria, X = biomass concentration, $S_{0}$  = influx substrate concentration, $K_{d}$  = decay rate, $α$  = biofilm retention constant, D = dilution rate, t = time.	[31]
$\frac{dS}{dt} = - q_{a} X_{a} - q_{m} X_{m} + D (S_{0} - S)$
$\frac{{dX}_{a}}{dt} = - μ_{a} X_{a} - K_{d, a} X_{a} - α_{a} D_{X_{a}}$
$\frac{{dX}_{m}}{dt} = - μ_{m} X_{m} - K_{d, m} X_{m} - α_{m} D_{X_{m}}$
Conduction based model	Steady state mass balance for substrate based on diffusion and convection. Dynamic mass balance for the active and inactive bacteria based on accumulation, advection, growth and decay of the two microbial communities in the biofilm. $D_{s, f}$  = diffusion coefficient of substrate in the biofilm, $ϕ_{a}$ and $ϕ_{i}$  = volumetric fraction of active and inactive biomass, $X_{f, a}$ and $X_{f, i}$  = density of active and inactive biomass.	[28]
$D_{s, f} + \frac{\partial^{2} S}{\partial z^{2}} = X_{f, a} q$
$\frac{\partial ϕ_{a}}{\partial t} + \frac{\partial (v ϕ_{a})}{\partial z} = Yq - r_{res} - r_{ina}$
$\frac{\partial ϕ_{i}}{\partial t} + \frac{\partial (v ϕ_{i})}{\partial z} = \frac{X_{f, a}}{X_{f, i}} r_{ina}$
Multidimensional model	Applicable for both continuous and batch mode ( $ϕ$  = 0), this model provides the biomass and substrate material balances in both biofilm and the bulk liquid. The bulk liquid is assumed to be completely mixed, whereas biofilm is characterized by spatial concentration gradients. Subscript F and B refer to biofilm and bulk liquid respectively. D = diffusion coefficient, $ϕ$  = volumetric flowrate, $S_{in}$ and $X_{in}$  = initial substrate and biomass concentration, $r_{S, B}$ and $r_{X, B}$  = net substrate reaction rate and net biomass reaction rate in the bulk, $r_{S, F}$  = net substrate reaction rate in the biofilm, $r_{S, E}$  = electrochemical rates of solute component change on the electrode surface, $r_{\det}$ and $r_{ata}$  = net biomass detachment and attachment rates, $v_{B}$  = bulk liquid volume.	[29]
Biofilm
$\frac{\partial S_{F}}{\partial t} = \nabla \cdot ({DS}_{F}) + r_{s, F}$
Bulk Liquid
$\frac{{dS}_{B}}{dt} = \frac{ϕ}{v_{B}} (S_{in} - S_{B}) + r_{S, B} + \frac{1}{v_{B}} \int_{v_{F}} r_{S, F} dV + \frac{1}{v_{B}} \int_{A_{F}} r_{S, E} dA$
$\frac{{dX}_{B}}{dt} = \frac{ϕ}{v_{B}} (X_{in} - X_{B}) + r_{X, B} + r_{\det} \frac{A_{F}}{v_{B}} - r_{ata} \frac{A_{F}}{v_{B}}$

C: Electrochemical equations
Ohm’s Law	Used to calculate BES cell output voltage and current, accounting for activation, concentration and ohmic polarization losses. $V_{cell}$  = BES cell voltage, I = current, $R_{Ext}$  = external resistance, Subscripts C and A represent quantities at cathode and anode respectively, $E^{B}$  = ideal equilibrium cell potential, $η_{act}$  = activation overpotential, $η_{conc}$  = concentration overpotential, $η_{ohm}$  = ohmic overpotential.	[29]
$V_{cell} = {IR}_{Ext}$
$V_{cell} = (E_{C}^{B} - η_{c, act} - η_{c, conc})$
$- (E_{A}^{B} - η_{c, act} - η_{c, conc}) - η_{ohm}$
Nernst-Monod model	Expression for current distribution in the conductive biofilm matrix considering electron generation from biomass synthesis and self-oxidation. j = current density, $k_{bio}$  = biofilm conductivity, $η$  = local potential, $γ_{1}$ and $γ_{2}$  = electron equivalence of substrate and active biomass, $τ$  = time conversion factor, $f_{e}^{0}$  = fraction of electrons from substrate used for energy generation to support synthesis, $X_{f, a}$  = active biomass density, $r_{res}$  = specific rate of endogenous respiration.	[28]
$j = - k_{bio} \frac{d η}{dz}$
$0 = k_{bio} \frac{\partial^{2} η}{\partial z^{2}} - \frac{F γ_{1}}{τ} f_{e}^{0} X_{f, a} q - \frac{F γ_{2}}{τ} X_{f, a} r_{res}$
Ohm’s Law accounting mediator concentration	BES cell current based on ohmic, activation and concentration losses including mediator concentration. $E_{OCV}$  = open circuit voltage, $R_{Int}$  = internal resistance, $M_{red}$  = reduced mediator fraction, $∊$ is constant.	[31]
$I = \frac{E_{OCV} - η_{act} - η_{conc}}{R_{Ext} + R_{Int}} \frac{M_{red}}{∊ + M_{red}}$
Butler-Volmer equation	Standard equation to describe electrochemical kinetics considering both cathodic and anodic reactions at the same electrode. $I_{0}$  = exchange current density, $α$  = charge transfer coefficient, n = number of electrons involved in the reaction, $η_{a}$  = overpotential.	[21]
$I = I_{0} [\exp (\frac{α nF}{RT} η_{a}) - \exp (\frac{- (1 - α) nF}{RT} η_{a})]$
Butler-Volmer-Monod equation	Expression for current distribution derived by combining Butler-Volmer kinetics with enzyme kinetics (to represent biochemical conversion). $I_{\max}$  = maximum current density, $K_{1}$ and $K_{2}$  = lumped parameters, $K_{M}$  = substrate affinity constant, f =  $F / (RT)$ .	[45]
$I = I_{\max} \frac{1 - e^{- f η}}{K_{1} e^{- (1 - α) f η} + K_{2} e^{- f η} + (\frac{K_{M}}{S} + 1)}$

Marcus et al. [28] developed an important mathematical model describing the biofilm as a conductive solid matrix, which has a specific conductivity and accepts electrons from the biofilm bacteria and conducts them to the anode electrode without the needs of any electron shuttles. This approach is based on the experimental findings of certain type of bacteria that allowed direct (mediatorless) transfer of electrons to the electrode [46], [47]. This dynamic, one-dimensional model considers two microbial species in the biofilm domain [28]. In addition to the active bacteria which contributed to substrate utilization, this model also included a diffusive non-conductive layer (made up of inactive microbes) between the conductive matrix and the bulk anodic liquid. Ohm’s law is used to calculate the current density and a novel Nernst-Monod equation is derived to describe the relationship between the rate of carbon source consumption, its concentration, and the electrical potential [28]. Here the Nernst model which is typically used by electrochemists to describe redox potential is combined with the Monod kinetics used by biologists to describe the dependence of biological growth on the concentration of electron donor/acceptor to develop the Nernst-Monod equation that described the relation between bacterial kinetics, substrate concentration and the electric potential. The model includes steady-state mass balance of substrate in the biofilm based on molecular diffusion and consumption rate and a dynamic mass balance or the biomass (active and inert) based on the growth, respiration and decay. The conductivity of the matrix has been linked to the current density and local voltages along the biofilm depth. Marcus et al. [28]’s model is considered an important milestone in understanding electron transfer mechanisms and describes the relations between concentration of the substrate, local potential values, biofilm conductivity and the concentration gradient of the species involved in the process. A representative result from Marcus et al. [28]’s study is shown in Fig. 4, describing the change in current density and steady state profiles of the local potential ( $η$ ), substrate and active biomass volume fractionat different detachment rates. This model predicts MFC performance trends that have been observed before, however it does not include any direct experimental comparison [28].

Marcus et al. [28] model served as a basis for many advanced direct conduction based models developed in future. For example, Merkey and Chopp [36], extended Marcus et al. [28]’s work to develop a two dimensional model for studying the influence of anode geometry on the MFC performance. This model is validated with experimental data and used for studying the effect of anode numbers, fluid flow speed and anode density on current production [36]. In a follow-up study Merkey and Chopp [48] extended their previous model [36], to study the competitive growth characteristics between two anode-respiring bacterial species, one that utilize a diffusive mediator, other that utilizes a conductive extracellular polymer (EPS) matrix to transfer electrons to the anode. The competition between the two species for space and nutrients is explored and it is found that the bacteria that conducted electrons using the EPS matrix show optimal growth [48]. Renslow et al. [49] also developed a biofilm model considering dual extracellular electron transfer mechanisms.

Sedaqatvand et al. [50] extended the conduction based approach of Marcus et al. [28] and combined with Genetic Algorithm to estimate the design parameters of a single chamber MFC treating dairy wastewater. They found that in a system with concentration boundary layer and biofilm conductivity as the main resistances, the contributions of ohmic and concentration overpotentials are almost equal in dropping cell voltage [50]. Alavijeh et al. [22] also used Marcus et al. [28]’s model as a basis to develop a general microbial electrochemical cell model that can be used to study both microbial fuel cell as well as microbial electrolysis cell. Though very similar to Marcus et al. [28]’s formulation, this model considers Bernard’s anaerobic digestion kinetics at the anode and in case of MEC it also provides an expression to calculate the net volumetric hydrogen production rate at the cathode based on the cathode efficiency [22]. Kazemi et al. [23] adopted the conductive biofilm approach and developed the first model for MES. Applying Marcus et al. [28]’s approach to model a biocathode, this 1D dynamic model describes microbial based electrosynthesis of organic compounds (acetate) and can provide useful information regarding electron transfer in biofilms and kinetic parameters for bacterial growth [23]. Recently, Teleken et al. [51] also used the conductive biofilm approach to model the bioanode of an MFC inoculated with marine microorganisms.

Other than the seminal model of Marcus et al. [28], which has been adopted and expanded in numerous other studies, another benchmark model was developed by Pinto et al. [31]. In this dynamic model based on ODEs, Pinto et al. [31] describes the anodic chamber of a single chamber MFC considering two microbial populations (anodophilic and methanogenic bacteria). The charge transfer between the substrate and the anode is based on an intracellular mediator, however extracellular electron transfer via nanowires or direct contact with the anode is also considered. The microbial populations are assumed to be both attached (anodiphilic and methanogenic) and suspended (methanogenic). Substrate (acetate) is assumed to be uniformly mixed in the anodic chamber and the biofilm formation and retention is simulated using a two-phase growth-washout model. Growth of anodiphilic bacteria is described by the multiplicative Monod kinetics and mass balance for substrate and intracellular mediators is also described. The expression for current output is derived using Ohm’s law and the voltage over-potentials [31]. The model parameters are estimated using the Nelder-Mead simplex algorithm and the model is then used to study the influence of organic load and external resistance on MFC power output and long-term system performance. This ODE based simple model is easy to implement, allows fast numerical simulations and can be used for both process control and optimization [31]. In a follow up study Pinto et al. [35] extended the model to describe MEC operation and predict $H_{2}$ production rate. In this 1D dynamic model, the two population model described in the previous study was combined with the anaerobic digestion model proposed by Bernard et al. [52] under the assumption that anaerobic degradation of wastewater can be described by a single hydrolysis and fermentation step of complex organic matter conversion to acetate [35]. This is the first model that described $H_{2}$ production from complex organic matter in an MEC [35].

Ping et al. [31]’s model was also extended further by Ping et al. [24] to simulate the dynamic behaviour of a microbial desalination cell. This model [24] is also based on ODEs similar to Pinto et al. [31], but in addition to the mass balance for the substrate, microorganisms and the mediators, the mass balance for salt has also been described. After obtaining the model parameters by fitting with experimental data from small lab-scale MDC system, the model is used to predict the effect of different parameters (substrate flow rate, external electrical resistance, salt solution flow rate) on performance of the MDC. The model is also validated with experimental data from a large-scale MDC system [24]. Ping et al. [24]’s model was further extended to study brackish water desalinationand wastewater treatment, boron removal using different BESs [53], [41]. Recio-Garrido et al. [54] combined the model equations described by Pinto et al. [31]with the equivalent electrical circuit model for of an MFC to understand the effect of charge storage on the fuel cell performance. This combined bioelectrochemical-electrical model allowed for both process optimization (that can be performed offline) as well as online approach that allows real time estimation of electrical parameters such as internal capacitance (C), open circuit voltage ( $E_{oc}$ ) and internal resistance of the system, as the simulations are run together with the experiment. This model presents a guiding pathway for development of software sensors for process control and online monitoring of MFCs [54]. Nakasugi et al. [55] also used Pinto et al. [35]’s approach as a basis to model electromethanogenesis (EM) in a BES.

3.1. Anode and cathode combined analysis

All the models discussed so far are limited to the analysis of a single electrode (anode or cathode) of a BES. As has been highlighted in several studies, both the electrodes of BES influence the performance of the process [9], [19]. In order to obtain a thorough understanding of the BES, it is important to develop coupled models that include the phenomena occurring at both anode and cathode and should simultaneously simulate both the fast electrical dynamics and mass transfer processes (milliseconds to seconds) along with the relatively slow dynamics of microbial growth dynamics (hours to days) [19].

The first model for BES that considered the phenomena in both anode and cathode chambers was developed by Zeng et al. [34]. This work is based on similar models developed previously for chemical fuel cells such as direct ascorbic acid fuel cells and direct methanol fuel cells [34]. In this two chamber model, both the bio-electrochemical and the electrochemical reactions occurring at anode and cathode respectively are modeled using Butler-Volmer expressions. Protons and cations are neglected in the cathode reaction, however. Both anode and cathode chambers are assumed to be perfectly mixed, and thus the mass balance of components in anode and cathode chambers only varies in time, as a function of the corresponding reaction rates. The charge balance at the anode and cathode is based on the cell current density, the respective capacitances and the reaction rates [34]. The total cell voltage is calculated after accounting for the voltage losses due to activation and concentration over-potentials as well as the membrane and solution resistances. The model parameters are estimated by fitting with experimental data and the model is then used to simulate both steady state and dynamic performance of the MFC as a function of operating parameters such as the acetate feed flow-rate, acetate feed concentration. The model is tested with both simple (acetate) and complex (artificial wastewater) substrate feed. While this is the first model to develop a coupled solution considering both the electrodes, one of the major limitation of this study is that it does not consider the biofilm characteristics at the anode which have been shown to significantly affect the performance of the system. However the model is very easy to implement and can be used as an effective tool for fast optimization studies of MFC and also serves as a good basis for the development of more detailed two-chamber models [34].

Oliveira et al. [37] extended Zeng et al. [34]’s model by including heat balance and biofilm formation and developed a more comprehensive two chamber model for MFC performance analysis. In this 1D steady state model, the bio-electrochemical reaction occurring at the anode is modeled using Tafel and Monod equations and the electrochemical reaction at cathode is described by Tafel equation. Effective Fick model is used to describe the mass transfer in the electrodes and the biofilm, and heat balance is based on Fourier’s law. Interface concentrations of the components are described using partial coefficients assuming local equilibrium [37]. The model predictions are compared with both experimental and previous simulation studies and the model is found to show the correct trends of the influence of current density on the anode and cathode overpotential, on the biofilm thickness, temperature and concentration profiles [37]. With a simple 1D steady state formulation this model is quite easy and computationally less straining to solve and can be used for quick optimization studies [37]. Oliveira et al. [37]’s model is an improvement over Zeng et al. [34]’s approach, however it does not include dynamic analysis and thus cannot be used to study and understand how operational parameters influence the MFC performance over time. Also, though this model considers the biofilm and includes the Monod kinetics in the anode electrochemical equation, the biofilm is assumed to remain constant assuming equal microbial growth and biomass losses [37]. This assumption significantly reduces the biofilm functionality in the model [37].

Yao et al. [39] further extended the dual chamber MFC models proposed by Zeng et al. [34] and Oliveira et al. [37], by developing a 2D two phase mass transport model for MFC. This model assumes a steady state mass transport, and does not include diffusion of CO2, O2 and acetate into the membrane. An agglomerate model has been used to describe the mass transport process in the cathode catalyst layer. The local over-potential is calculated assuming proton transport in liquid phase and electron transport in the solid phase of the MFC. The model domain included anode chamber (represented by the biofilm and the anode electrode layer), the membrane and the cathode chamber (represented by the cathode catalyst layer and the cathode electrode layer). Everything except the cathode electrode layer is considered as the liquid phase region for electric potential calculations. Reactions at the anode and cathode are represented by the Tafel-Monod expression and the Tafel-like expressions respectively and mass conservations equations were based on the classical two-phase flow theory. To simplify the calculations, the microbial composition is assumed to be uniform over the biofilm and due to steady state assumption the rate of change of biomass over time is also considered zero. The 2D model is solved using the finite volume method and is validated against experimental data which showed good agreement. Subsequently it is used to study the effect of the biofilm and solution conductivity and it is found that while biofilm conductivity had a continuous linear influence on improving the cell performance, the ionic conductivity reaches a plateau after an initial improvement. The mass transfer results show a concentration gradient in the x direction for acetate, while oxygen concentration in the porous cathode show a nearly uniform distribution [39]. Gas-liquid two-phase flow typically occurs in an MFC and this model presents the first formulation to model this two phase flow [39]. However it has a lot of scope for improvement in future by providing a more dynamic analysis with a detailed biofilm growth model and also improving the internal distribution of products and reactants in the model.

Sirinutsomboon [38] developed a 1D dynamic model for a single chamber membraneless MFC considering both anode and cathode. In this study, sucrose (which is a primary sugar of Molasses, a by-product of the sugar industry) is used as a substrate for the anode bacteria and a layer of polytetrafluoroethylene(that is permeable to oxygen) is used to separate the anolyte from the cathode. The rate of substrate consumption at the anode is described using the Nernst-Monod equation, while the oxygen reduction reaction at the cathode is expressed using Monod and Butler-Volmer kinetics. Diffusion of oxygen in the cathode electrode is described by Fick’s second law [38]. The biofilm description in this model is similar to that by Marcus et al. [28]. Biofilm is assumed to be a conductive matrix and the local potential is calculated based on Ohm’s law and the steady-state electron balance [38]. The simulation program for this model is developed in a visual basic interface and is used to study the effect of operational parameters such as the initial substrate concentration, biofilm thickness, cathode thickness, etc. on the system performance. This model does not describe any expressions for change in active biomass concentration and thus the biofilm thickness basically remains the same as the initially selected value [38]. chamber batch MFC model [42] developed a two chamber batch MFC model considering both electrodes based on a lumped formulation. The model consists of three domains, bulk liquid in the anode chamber, biofilm attached to anode and bulk liquid in the cathode chamber. Lactate is assumed to be the substrate at anode, which is reduced by the bacteria to release $H^{+}$ ions and electrons. Electrons are assumed to be transferred to the anode via the direct conduction mechanism proposed by Marcus et al. [28]. Three kinetic models are tested to calculate the bacterial growth rate, namely the Monod equation, Blackman model and the Tessier model. These growth rates are substituted in the Nernst-Monod equation to derive the rate of substrate consumption. Expression for mass balance in the biofilm of the active and inactive biomass, substrate, CO2 and $H^{+}$ ions are described. Additionally, mass balance for substrate and CO2 in the anode bulk liquid and O2 in the cathode bulk liquid are described. The total MFC output voltage is calculated based on the Ohmic, activation and concentration losses. Model parameters are estimated using a parametric estimation study based on experimental data. The model predictions of voltage and current are subsequently compared with experimental results and an excellent agreement is obtained. It is also shown that the Monod model predicts the substrate concentration more accurately as compared to the Backman and Tessier models [42]. This batch MFC model [42]is extended to a continuous two chamber MFC model by Esfandyari et al. [43]. These simple models are quite useful in quick performance testing of MFC voltage and current. However the lumped formulation assumes that all quantities are uniformly distributed and no change occurs spatially, which is a major limitation of this approach [42], [43]. Many studies in the past have shown that the substrate and other components have a spatial gradient, particularly in the biofilm which influences the dynamic performance of the BES.

Ismail and Habeeb [56] combined the approaches used in previous models [32], [34], [37] and developed a two chamber MFC model by integrating the macro-scale dynamic mass balance for solutes and biomass in the bulk liquid with the micro-scale phenomena in the biofilm represented by a 2D model. The fluxes are integrated over the open boundaries of the micro-scale domain to link the two scales in the model [56].

Ou et al. [57], [58], [59] published a series of studies focused on developing steady state and transient mathematical models for studying single chamber air cathode MFC systems. It is found that electrical migration did not have a major impact on the power densities of MFC [57]. It is also found that the diffusion and dissolved oxygen content in the cathode are the crucial parameters influencing the performance of the air-cathode MFC [58]. The steady state model showed that PBS buffer solution performed better compared to other buffers (NaHCO3, N $H_{4}$ Cl) for pH neutralization [59].