1. Introduction
A manipulator (robot arm) is considered to be the most suitable tool for executing subsea intervention operations. Hence, unmanned underwater vehicles (UUVs) such as remotely operated vehicles (ROVs) and in some cases, autonomous underwater vehicles (AUVs) are equipped with one or more underwater manipulators. UUVs with manipulators are often called Underwater Vehicle Manipulator Systems (UVMS). The majority of existing underwater manipulators used on UUVs are anthropomorphic, i.e. they are designed to resemble a human arm. These manipulators are composed of a sequence of rigid bodies (links) interconnected by means of revolute joints with a suitable angular displacement between them and grippers or other interchangeable tools attached at the end-effector. For the observation of their surroundings they are usually accompanied with additional equipment comprising of one or more cameras and spotlights mounted on the base underwater vehicle and/or on the manipulator itself.
Underwater manipulators are used for a variety of subsea tasks in different applications within offshore oil and gas, marine renewable energy (MRE) and marine civil engineering industries as well as in marine science and military applications (Capocci et al., 2017). As they are being used in a wide range of applications, subsea manipulators are designed for different purposes, e.g. there are manipulators with limited mobility equipped with grippers for lifting large, heavy objects, manipulators used for fixing a detachable gripper to a selected, sunken object, grabber manipulators equipped with grippers or vacuum cups used to fix an underwater vehicle to submerged structures or near flat walls during the operation, manipulators equipped with inspection devices, dexterous intervention manipulators with grippers that can carry different tools used for repair and maintenance operations on submerged structures, etc. Usually, work class ROVs are equipped with two manipulators, in most cases one simple powerful grabber to hold the ROV near the hydro engineering structure or wreck, while the other manipulator performs the actual intervention task.
Some of the tasks underwater manipulators are designed to execute include pipe inspection (Christ and Wernli, 2014), salvage of sunken objects (Chang et al., 2004), mine disposal (Fletcher, 2000), cleaning surfaces (Davey et al., 1999), opening and closing valves, drilling, rope cutting (Christ and Wernli, 2014), cable laying and repair, clearing debris and fishing nets, biological (Jones, 2009) and geological sampling (Noé et al., 2006), archaeological work (Coleman et al., 2003), etc. In general, manipulators are located at the front side of the underwater vehicle, but this is not always the case, e.g there are vehicles with a manipulator located at the bottom side (Ribas et al., 2012).
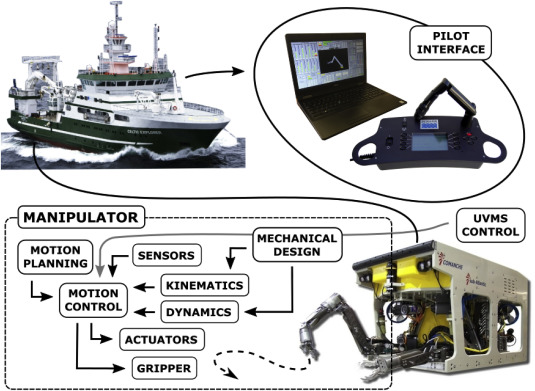
A brief overview on underwater manipulators can be found in the underwater robots review paper by Yuh and West (2001). Antonelli (2014) provided a good theoretical background for underwater manipulators from the modeling and control point of view. However, a complete article encapsulating relevant practical and theoretical knowledge, state of the art technology as well as up to date research done in this area can not be found in the literature. Therefore, the aim of this paper is to provide a review of underwater manipulators covering all the relevant aspects, from an applied underwater research point of view. Fig. 1outlines the factors governing performance for underwater manipulation, which are expanded upon in detail within this paper.
 Fig. 1. Factors affecting underwater manipulator performance.
Fig. 1. Factors affecting underwater manipulator performance.The remainder of the paper is organized as follows: Section 2 describes mechanical design features and capabilities of existing underwater manipulators and gives their comparison. Section 3 analyses underwater manipulator actuation methods. Section 4 describes control systems of commercially available subsea manipulators. Sections 5 Underwater manipulator motion control, 6 UVMS motion control cover academic research achievements in the area of motion control for underwater manipulators and underwater vehicle-manipulator systems respectively. The state of the art in kinematics control and motion planning algorithms is covered in section 7, while section 8 focuses on force control algorithms. Finally, Section 9 presents conclusion.
2. Mechanical design
In order to be able to operate in deep waters and cope with the harsh conditions of subsea environment, specialised materials are used in the construction of underwater manipulators. Additionally, depending on the task for which they are designed, underwater manipulators have to meet relevant requirements regarding the size of the workspace in which they are to operate, lifting capacity, wrist torque, etc. Table 1 lists specifications of existing commercial underwater manipulators.
Table 1. Specifications of existing commercial underwater manipulators.
| Manufacturer | Model | Actuation | DOF | Weight in air [kg] | Weight in water [kg] | Lift capacity max nom. (full ext.) [kg] | Wrist torque [Nm] | Grip force [kgf] | Depth rating [m] | Max. reach [m] | Power Source | Material | Actuators | Sensors | Control | Price [$] |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ansaldo | MARIS 7080 | Electric | 7 | 65 | 45 | 8 (/) | / | 20.4 | 6000 | 1.4 | 72VDC | Al | BLDC | Resolvers, F/T | Semi Automatic | / |
| Cybernetix | Maestro | Hydraulic | 6 | 85 | 65 | 100 (96) | 190 | 150 | 6000 | 2.4 | 50 Hz 220VAC 210bar 18lpm | Ti | Rot. vane & gerotor | Resolvers | Pos. & force fb. | 1m |
| Eca Hytec | Arm 7E | Electric | 6 | 69 | 49.2 | 40 (40) | 25 | 80 | 6000 | 1.79 | 24-36VDC | Al 6082 T6 | BLDC in oil | / | Prop. & torque | 110k |
| Eca Hytec | Arm 7E Mini | Electric | 6 | 51 | 30 | 25 (25) | 25 | 50 | 3000 | 1.44 | 24-36VDC | Al 6082 T6 | BLDC in oil | / | Prop. & torque | 110k |
| Eca Hytec | Arm 5E | Electric | 4 | 27 | 18.5 | 25 (25) | 25 | 60 | 6000 | 1 | 24-30VDC | Al 6082 T6 | BLDC in oil | / | Prop. | 40k |
| Eca Hytec | Arm 5E Mini | Electric | 4 | 23 | 15 | 25 (25) | 25 | 50 | 6000 | 0.85 | 24-40VDC | Al 6082 T6 | BLDC in oil | / | Prop. | 40k |
| Eca Hytec | Arm 5E Micro | Electric | 4 | 10 | 2.7 | 10 (10) | 10 | 50 | 6000 | 0.64 | 24-30VDC/240VAC | Al 6082 T6 | BLDC in oil | / | Prop. | 25k |
| Forum Perry | TA40 | Hydraulic | 6 | 98 | 65 | 125 (210) | 150 | 509 | 11000 | 2 | No electrical 210bar 9lpm | Al, SS | Cylinders, rot. vane & gerotor | No | Pos./Rate/Hybrid fb. | / |
| Forum Perry | TA60 | Hydraulic | 4 | 82 | 60 | 380 (300) | 250 | 509 | 11000 | 1.44 | No electrical 210bar 9lpm | Al, SS | Cylinders, rot. vane & gerotor | No | Rate/Hybrid fb. | / |
| Forum Perry | TA60J | Hydraulic | 4 | 76 | 51 | 380 (300) | 250 | 509 | 11000 | 1.38 | No electrical 210bar 9lpm | Al, SS | Cylinders, rot. vane & gerotor | No | Rate/Hybrid fb. | / |
| Forum Perry | TA16 | Hydraulic | 4 | 50 | 40 | 147 (102) | 108 | 226 | 11000 | 1.06 | No electrical 210bar 9lpm | Al, SS | Cylinders, rot. vane & gerotor | No | Rate/Hybrid fb. | / |
| Graal Tech | UMA | Electric | 6 (7) | 28 | 14 | 10 (/) | / | / | 100 | 1 | 24VDC | Al | BLDC | Yes | Position | 75k |
| Hydro-Lek | 40400 | Hydraulic | 4 | 45 | 30 | 150 (210) | 75 | / | 11000 | 1.42 | 210 bar | SS 316, Al HE30, PE | Cylinders & gerotor | No | Rate | 16k |
| Hydro-Lek | 40500(R) | Hydraulic | 6 | 59 | 40 | 150 (210) | 75 | / | 11000 | 1.5 | 210 bar | SS 316, Al HE30, PE | Cylinders & gerotor | No | Rate | 30k |
| Hydro-Lek | 43000 | Hydraulic | 4 | 6 | 4 | 10 (20) | 8 | / | 11000 | 0.53 | 160 bar | SS 316, PE | Cylinders & gerotor | No | Rate | 4k |
| Hydro-Lek | CRA6 | Hydraulic | 5 | 28 | 14.5 | 32 (32) | 38 | / | 11000 | 1.5 | 140 bar | SS 316, Al HE30, PE | Cylinders & gerotor | No | Rate | 12k |
| Hydro-Lek | EH5 | Hydraulic | 4 | 12 | 9.5 | 25 (25) | 14 | / | 11000 | 0.8 | 140 bar | Al E30, SS 316 | Cylinders & gerotor | No | Rate | 7k |
| Hydro-Lek | HD5 | Hydraulic | 4 | 21.5 | 16.5 | 40 (40) | 38 | / | 11000 | 0.819 | 140 bar | SS 316, Al HE 30, PE | Cylinders & gerotor | No | Rate | 9k |
| Hydro-Lek | HD6W HD6R | Hydraulic | 5 | 29 | 21 | 40 (40) | 38 | / | 11000 | 1.12 | 140 bar | SS 316, Al HE30, PE | Cylinders & gerotor | No | Rate | 12k |
| Hydro-Lek | MB4 | Hydraulic | 3 | 13.3 | 11 | 40 (40) | 40 | / | 11000 | 0.63 | 140 bar | SS 316, Al HE30, PE | Cylinders & gerotor | No | Rate | 5k |
| Hydro-Lek | RHD5(W) | Hydraulic | 4 | 30 | 20 | 80 (80) | 38 | / | 11000 | 0.95 | 210 bar | SS 316, Al HE30, PE | Cylinders & gerotor | No | Rate | 11k |
| ISE Ltd. | Magnum 7 | Hydraulic | 6 | 63.5 | 30 | 454 (295) | 108 | 205 | 11000 | 1.5 | 70bar 19lpm | Al, SS | Cylinders | Potentio-meters | Pos./Rate | 59k |
| ISE Ltd. | Magnum 5 | Hydraulic | 4 | 50 | 27 | 454 (295) | 108 | 160 | 5000 | 1.16 | 70bar 19lpm | Al, SS | Cylinders | Yes | Pos./Rate | 52k |
| ISE Ltd. | Magnum 6 Mini | Hydraulic | 5 | 57 | 30.6 | 454 (317) | 108 | 160 | 5000 | 0.96 | 70bar 19lpm | Al, SS | Cylinders | No | Rate | 56k |
| ISE Ltd. | Magnum 5 Mini | Hydraulic | 4 | 34 | 24 | 68 (23) | 14 | 35 | 5000 | 0.71 | 35bar 19lpm | Al, SS | Cylinders | No | Rate | 46k |
| KNR Systems Inc. | HYDRA UW3 | Hydraulic | 6 | 130 | / | 300 (121) | 350 | 300 | 500 | 2.035 | 210bar 19lpm | Al, SS, Ti | Cylinders & rotary vane | Encoders | Position | 175k |
| Kraft | Predator | Hydraulic | 6 | 80 | 51 | 227 (91) | 135 | 135 | 6500 | 1.64 | 50 Hz 220VAC 210bar 19lpm | Al, SS | Cylinders, rot. vane & gerotor | Yes | Pos. & force fb. | 200k |
| Kraft | Raptor | Hydraulic | 6 | 75 | 44 | 227 (91) | 135 | 135 | 6500 | 1.52 | 50 Hz 220VAC 210bar 19lpm | Al, SS | Cylinders, rot. vane & gerotor | Yes | Pos. & force fb. | 200k |
| Kraft | Grips | Hydraulic | 6 | 59 | 41 | 82 (45) | 20 | 90 | 3000 | 1.556 | 50 Hz 220VAC 210bar 11lpm | Al, SS | Cylinders, rot. vane & gerotor | Yes | Pos. & force fb. | 200k |
| Ocean Innovation System | BE5-500 | Electric | 4 | 15 | 8 | /(16) | 1.6 | 100 | 500 | 0.7 | 24 VDC | Al 5083, PE | BLDC | Hall | Rate | 30k |
| Oceaneering | Atlas Hybrid | Hydraulic | 6 | 73 | 50 | 454 (250) | 205 | 454 | 6500 | 1.66 | 90-260VAC 206bar 19lpm | Al 6061 T6, SS | Cylinders, rot. vane & gerotor | Solid State Pos. | Hybrid Pos./Rate | / |
| Profound Technology | M1P | Hydraulic | 6 | 115 | 77 | 275 (250) | 175 | 652 | 4000 | 2.1 | / | Al, SS | Cylinders & rotary | Yes | Pos./Rate | / |
| Schilling | Titan 2 | Hydraulic | 6 | 80 | 61 | /(109) | 68 | 136 | 6500 | 1.92 | 90-260VAC 210bar 19lpm | Ti | Cylinders, rot. vane & gerotor | Resolvers | Pos. & force fb. | / |
| Schilling | Titan 3 | Hydraulic | 6 | / | / | /(/) | / | / | 6500 | 1.92 | 90-260VAC 210bar 19lpm | Ti | Cylinders, rot. vane & gerotor | Resolvers | Pos. & force fb. | / |
| Schilling | Titan 4 | Hydraulic | 6 | 100 | 78 | 454 (122) | 170 | 417 | 7000 | 1.92 | 90-260VAC 210bar 19lpm | Ti | Cylinders, rot. vane & gerotor | Resolvers | Pos. & force fb. | / |
| Schilling | Conan 7P | Hydraulic | 6 | 107 | 73 | 273 (159) | 205 | 454 | 3000 | 1.8 | 90-260VAC 210bar 19lpm | Al 6061, SS | Cylinders, rot. vane & gerotor | Potentio-meters | Pos. | / |
| Schilling | Orion 7P/7R | Hydraulic | 6 | 54 | 38 | 250 (68) | 205 | 454 | 6500 | 1.85 | 90-260VAC 210bar 19lpm | Al, SS | Cylinders, rot. vane & gerotor | Potentio-meters | Pos./Rate | / |
| Schilling | Atlas 7R | Hydraulic | 6 | 73 | 50 | 500 (250) | 205 | 454 | 6500 | 1.66 | 90-260VAC 210bar 19lpm | Al 6061 T6, SS | Cylinders, rot. vane & gerotor | No | Rate | / |
| Schilling | RigMaster | Hydraulic | 4 | 64 | 48 | 270 (181) | 205 | 454 | 6500 | 1.37 | No electrical 210bar 19lpm | Ti, Al, SS 630 | Cylinders, rot. vane & gerotor | No | Rate | / |
| Schilling | Orion 4R | Hydraulic | 3 | 30 | 21 | 136 (/) | 205 | 454 | 6500 | 0.68 | No electrical 210bar 19lpm | Al, SS | Cylinders rot. vane & gerotor | No | Rate | / |
| Seamor | 7F-H-ARM | Hydraulic | 6 | 32 | / | /(5) | / | / | 300 | 1.07 | 300V 35bar 4.5lpm | SS 316, Al 6061 T6 | / | / | / | / |
| TitanRob | M700 | Hydraulic | 6 | 30 | 20 | 50 (40) | 45 | 80 | 3000 | 1.05 | 140 bar min 1.5lpm | Ti, SS 316 | Cylinders, rot. vane & gerotor | No | Rate | 45k |
| TitanRob | G500 | Hydraulic | 4 | 20 | 15 | 100 (80) | 80 | 250 | 3000 | 0.8 | 140 bar min 1.5lpm | Ti, SS 316 | Cylinders & rotary | No | Rate | 40k |
| TitanRob | M501 | Hydraulic | 4 | 14 | 11 | 50 (40) | 45 | 80 | 3000 | 0.95 | 140 bar min 1.5lpm | Ti, SS 316 | Cylinders & rotary | No | Rate | 35k |
| Western Space & Marine | The ARM | Hydraulic | 6 | 145 | 97 | 45.4 (29.5) | / | 150 | 11000 | 1.7 | 24VDC 204bar 7.6lpm | / | / | / | Force fb. | / |
| Western Space & Marine | MK37 | Hydraulic | 6 | 43 | 16 | 23 (/) | / | 114 | 11000 | 0.94 | 24(15)VDC 204bar 4.5lpm | / | / | / | Force fb. | / |
Note./- Information not available; Pos. - Position; Prop. - Proportional; Fb. - Feedback.
The most common materials used in construction of underwater manipulators are metal alloys such as titanium Ti 6–4, anodized aluminium alloys (5083, 6082 T6, 6061 T6, 7075 T6, A356), stainless steel alloys (316, 630, 660), as well as some plastics (Polyethylene). The properties of these materials are relatively high strength and corrosion resistance and good machinability. To reduce the weight in the water and minimize the actuator burden, some experiments have been done on using buoyant materials on underwater manipulators (Ishimi et al., 1991). Typically, commercially available underwater manipulators are rated between 3000 and 6500 m of sea water (msw); however, some manipulators can operate in depths up to 7000 msw, e.g. Schilling Robotics Titan 4 and a prototype manipulator developed by Zhang et al. (2014). Additionaly, there are a some systems designed for full ocean depth (11000 msw). Woods Hole Oceanographic Institute in collaboration with Kraft Robotics designed one such manipulator for the purpose of Mariana Trench exploration mission (Bowen et al., 2008). Others include “Magnum 7”, a product of ISE Ltd. and, “The ARM” and “MK-37” developed by the Western Space and Marine, Inc.
The size of underwater manipulators is described by a parameter called “Reach” which represents the length of the whole manipulator kinematic chain. Along with the range of motion of joints, it determines the size of manipulator workspace, a set of points that can be reached by its end-effector (Cao et al., 2011). Reach of existing underwater manipulators ranges from 0.5 m for the grabber manipulators up to 2.4 m for heavy duty manipulators.
Maximum wrist torque which underwater manipulators are capable of producing ranges from 8Nm to 250Nm. According to ISO 13628–8:2002 (ISO 13628–8, 2002), rotary low torque ROV interfaces on subsea production systems, which are typically used on subsea tree needle valves, are rated to maximum 75Nm. Additionally, lifting/carrying (payload) capacity for underwater manipulators ranges from 5 kg up to 500 kg. Manufacturers often provide different parameters for manipulator lift capacity (“max. nominal”, “at full extension”, “at rated speed”, “through envelope”, etc.) which makes the comparison non-trivial as the carrying capacity is not a fixed value but depends on the pose of the manipulator.
Underwater manipulator weight (in air) is between 6 kg and 150 kg; however, their weight in water is more important, as it determines the buoyancy needed on the base vehicle in order to compensate for the manipulator. The weight and size are very important factors as they are directly responsible for the amount of dynamic coupling introduced between the manipulator and the underwater robot on which it is mounted and can thus influence the performance of the whole system. In order to be able to fully exploit manipulator characteristics, the manipulator weight should be a low enough percentage of the whole underwater robot weight, so that the dynamic coupling can be neglected or at least taken into account as an external disturbance that can be dealt with by the dynamic positioning of underwater robot (if this exists). Higher weight and bigger size bring about higher demands concerning the robustness of underwater robot thruster system to the disturbance caused by the dynamic coupling. In future research this constraint might be relaxed. Table 2 presents relative manipulator-to-vehicle weight for the typical commercial heavy, medium and light work class ROVs. It can be seen that this ratio is significantly low even for the light work class commercial vehicles.
Table 2. Relative manipulator-to-vehicle weight for commercial heavy (H), medium (M) and light (L) work class ROVs.
| ROV | ROV Class | ROV weight in air [kg] | Manipulator | Manip. weight in air [kg] | Manipulator-ROV relative weight [%] |
|---|---|---|---|---|---|
| Oceaneering Nexus | H | 4700 | Schilling Atlas | 73 | 1.5 |
| Perry XLX-Evo | H | 5500 | Schilling Titan 4 | 100 | 1.8 |
| Oceaneering Millennium | H | 4000 | Schilling Titan 4 | 100 | 2.5 |
| Oceaneering Magnum | H | 3000 | Schilling Titan 4 | 100 | 3.3 |
| Perry XLX-C | H | 3000 | Schilling Titan 4 | 100 | 3.3 |
| Saab Seaeye Leopard | M | 1200 | Schilling Orion | 54 | 4.5 |
| Sub-Atlantic Comanche | M | 1130 | Schilling Orion | 54 | 4.7 |
| Saab Seaeye Panther-XT Plus | L | 800 | Schilling Orion | 54 | 6.7 |
| Saab Seaeye Cougar-XT | L | 580 | Hydro-Lek HD5 | 21.5 | 3.7 |
| Saab Seaeye Panther-XT | L | 500 | Hydro-Lek HD6R | 21.5 | 4.3 |
| Oceaneering Spectrum | L | 415 | Hydro-Lek HD5 | 21.5 | 5.2 |
| Sub-Atlantic Mohawk II | L | 395 | Hydro-Lek HD5 | 21.5 | 5.4 |
Note. H - Heavy Work Class; M − Medium Work Class; L - Light Work Class.
Underwater manipulators can be equipped with various types of grippers on the end-effector. The commercial ones come with different interchangeable grippers each of which has their own specific purpose. A common gripper type is one with parallel acting jaws which includes a slot for a standard T-bar handle (ISO 13628–8, 2002), and its primary function is grasping different objects and tools in a variety of subsea operations. Tooling is generally designed with a T-bar exactly for this purpose. Different grippers include three/four finger intermeshing jaws, two/three finger floating jaws, scissor jaws, suction foots, etc. Gripper actuators are usually hydraulic and the gripping force of commercially available grippers ranges from 35 kgf to 652 kgf.
Depending on the nature of the task for which they are designed, underwater manipulators come with different number of degrees of freedom (DOF). Both commercial and experimental underwater manipulators are usually designed with three to six DOFs without taking gripper's mobility into account. The reason for this is that three DOFs are sufficient for achieving an arbitrary position and six DOFs for both arbitrary position and orientation of the end-effector (tool) in the workspace (Spong et al., 2005). The term “n-function” is often used in the literature to describe the number of actuators contained in a manipulator and this term includes the gripper's mobility as well, so for example a seven function manipulator means that there are six actuators responsible for manipulator motion that provide six true DOFs plus one actuator for gripper (jaw) mobility. Underwater manipulators with seven or more DOFs (without gripper mobility) are not very common, but they do exist. True seven DOF manipulators are said to be inherently redundant from the kinematic point of view (Siciliano et al., 2009). This feature can play an important role in the automation of manipulators since the redundancy can be exploited for a secondary objective such as obstacle avoidance which will be discussed later. Some of the work with seven DOF underwater manipulators has been reported by Marani et al. (2009) and Ribas et al. (2015), and with eight DOF manipulator by Greig and Broome (1994). Some authors proposed a multi stage manipulator, a micro-macro manipulator concept having large positioning manipulator carrying a smaller manipulator for fine precision work (Ishimi et al., 1991; Asokan et al., 2003).
Any robotics application of underwater manipulators requires applying kinematics modeling planning and control algorithms. Underwater manipulators generally have serial-chain mechanical structure similar to industrial robot arms. There is much literature about robot kinematics that can be applied to underwater manipulators, some of which can be found in (Spong et al., 2005; Siciliano et al., 2009; Corke, 2011). Additional literature about vehicle-manipulator systems can be found in From et al. (2014), and more specific literature related to underwater vehicle-manipulator systems in Antonelli (2014).
3. Actuation
In the early 90's a few authors proposed and experimented on seawater driven actuators for subsea manipulators (Ishimi et al., 1991; Yoshinada et al., 1991). Some of the benefits of water hydraulics are low viscosity, high power density, non-flammable properties and zero environmental impact (Krutz and Chua, 2004). However, this actuation approach was abandoned over the years due to its various disadvantages such as corrosive and abrasive properties, lubricationand sealing issues, unsuitable working temperature range, etc. Today all the existing commercially available underwater manipulators and most of the experimental/prototype underwater manipulators developed for research purposes run on either oil hydraulic or electric power, both of which have their advantages and disadvantages. Denket (2006) proposed a hybrid power structure using both hydraulic and electric actuators for a single manipulator in order to have the benefit of both. However, this actuation method has not yet found use in the commercial sector. Biodegradable fluids have begun to be introduced to minimize the impact on the environment of fluid leaks.
3.1. Hydraulic manipulators
In general, hydraulic actuators are capable of producing an output force/torque much larger than the force applied on the input without the use of mechanical components such as gears and levers (direct drive), which is a necessity for the implementation with electric actuators. Thus, hydraulic systems have higher power to weight ratio (payload capability) which goes up to the order of three for the existing commercial hydraulic underwater manipulators, whereas that ratio is one or less for the electrical ones. For this reason and because they require fewer parts, hydraulic systems are more compact for the same carrying capacity. Additionally, hydraulic systems are inherently pressurized, i.e the internal pressure is higher than the ambient pressure so they are not as susceptible to the sea water ingress as are their electric counterparts. Another advantage of hydraulic systems is that they possess inbuilt protection against overload. Due to these benefits, the vast majority of commercial manipulators operating underwater are driven by hydraulic oil. Typically, actuators with limited motion such as piston cylinders and rotary vane actuators are used to drive manipulator joints. However, in some cases gerotors, which are a type of hydraulic motors with continuous motion, are used for wrist joint actuation. The medium used for power transmission, pressurized hydraulic fluid is conveyed from a reservoir to actuators through flexible hoses or rigid pipes by a hydraulic power unit (HPU - electrically driven pump and pressure regulator). The motion of hydraulic systems is controlled by regulating the hydraulic fluid flow. This is done by means of different electro-hydraulic valves such as directional control valves (“switching”/“bang-bang”), proportional valves or servo valves. These valves are located either in an external valve pack or are integrated in the body of the manipulator along with hoses/pipes and electronic circuits. In the latter case, inner manipulator chambers containing valves and accompanying electronic circuits are oil filled and pressurized by a pressure compensator, which maintains the internal pressure slightly above the external pressure.
Leading commercial manufacturers of hydraulic underwater manipulators are Kraft Telerobotics, Schilling Robotics, Cybernetix, Hydro-lek, among others. Some of the manipulators are presented in Fig. 2, Fig. 3, Fig. 4, Fig. 5. Apart from industrial manufacturers, a number of research groups have been designing and developing experimental/prototype hydraulic underwater manipulators. Some of the manipulators with specifications and robot configurations similar to the commercially available seven function manipulators used on work class ROVs have been reported by Yao et al. (2009) and Zhang et al. (2014). Conversely, Zuyao et al. (2011) focused on atypical configuration with less DOFs.
 Fig. 2. Kraft Raptor, Copyright © 2017 by Kraft TeleRobotics, Inc.
Fig. 2. Kraft Raptor, Copyright © 2017 by Kraft TeleRobotics, Inc. Fig. 3. Schilling Titan 4, Copyright © 2017 by TechnipFMC plc.
Fig. 3. Schilling Titan 4, Copyright © 2017 by TechnipFMC plc. Fig. 4. Cybernetix Maestro, Copyright © 2016 by Ifremer.
Fig. 4. Cybernetix Maestro, Copyright © 2016 by Ifremer. Fig. 5. Hydro-lek 40500R, Copyright © 2017 by hydro-lek.
Fig. 5. Hydro-lek 40500R, Copyright © 2017 by hydro-lek.Despite their numerous advantages, hydraulically driven manipulators have drawbacks. Unlike their electrical equivalents, they can feature poor positioning accuracy and are not suited for implementation of fine control of the interaction force with the environment during contact tasks (Terribile et al., 1993). These limitations are not substantial in the conventional master slave teleoperation, however, in the case of implementation of automatic robotic functions their significance is of great concern. Another drawback of hydraulic systems is leakage of minor amount of hydraulic fluid which is almost impossible to solve, and the necessity to protect fluids from contamination, both of which bring about demands for the highest quality standards and materials for manufacturing of components, making hydraulic systems more expensive. Moreover, hydraulic manipulators require complementary equipment such as hydraulic pump, reservoir, filters, regulators, valves, etc. Most work class ROVs are propelled by hydraulically actuated thrusters and, therefore, hydraulic power and equipment are already available on the base vehicles. However, this is not always the case, e.g. the available power can be insufficient for running both thrusters and the manipulator at the same time or if the vehicle's thrusters are electrically actuated it is less likely that the vehicle has a HPU. On the other hand, electrical power is the only additional requirement for an electrical manipulator and it can usually already be found on an underwater robot.
3.2. Electric manipulators
Electric underwater manipulators are less frequent in commercial use but are often custom made as prototypes for research purposes. Actuators which are commonly used are brushless DC (BLDC) electric motors with harmonic drive gears featuring low backlash and large reduction ratio. To stop water ingress, the actuators are oil filled, which also provides lubrication and cooling. Frequently, to avoid having external cables or possible entanglement, power and signal cables are fed through the same hoses used for pressure compensation (Terribile et al., 1994). Experimental prototypes using magnetic coupling mechanisms for transferring torque into joints as an alternative approach for watertightness can be found in Ishitsuka and Ishii (2007a) and Ishitsuka and Ishii (2007b). The main advantage of electrically driven manipulators is the capability for precise motion and force/torque control as they are inherently equivalent to the industrial robot arms. Depending on the nature of the task, electric underwater manipulators can find use in subsea intervention operations, however, for most industrial intervention tasks they often do not meet the speed, reliability and strength or force requirements (Hildebrandt et al., 2009a).
The leading commercial manufacturer of electric underwater manipulators is Eca Robotics, whose manipulator 7E is presented in Fig. 6.
 Fig. 6. Eca robotics 7E, Copyright © 2017 by ECA Group.
Fig. 6. Eca robotics 7E, Copyright © 2017 by ECA Group.One of the first articles addressing the design of electrically driven underwater manipulator was presented by Yoerger et al. (1991) where a three DOF manipulator was developed for the Woods Hole Oceanographic Institution'sJASON ROV. A six DOF electrical manipulator developed by Tecnomare and Ansaldo in Italy was reported in Terribile et al. (1994), having 2.1m reach with maximum payload of 30 kg. Another example of the early work can be found in Smith et al. (1994), where a five DOF manipulator called “Poseidon” was developed, consisting of 1m reach, operational depth of up to 100m and lifting capability of 5 kg. Collaborating with the Autonomous Systems Laboratory of the University of Hawaii for the SAUVIM AUV project, Ansaldo developed a seven DOF manipulator called “MARIS 7080” (Fig. 7) (Yuh et al., 1998; Marani et al., 2009). Rated for 6000m depth it has 1.4m reach and 6 kg payload at full extension.
 Fig. 7. Ansaldo Maris 7080, Copyright © 2006 by autonomous systemslaboratory.
Fig. 7. Ansaldo Maris 7080, Copyright © 2006 by autonomous systemslaboratory.Two seven DOF manipulators also developed by Ansaldo were used within the AMADEUS project (Lane et al., 1997; Casalino et al., 2001) for cooperative sampling. In 2007, the Space System Laboratory at the University of Maryland teamed with the Woods Hole Oceanographic Institute and developed a six DOF Subsea Arctic Manipulator for Underwater Retrieval and Autonomous Interventions (“SAMURAI”) (Lewandowski et al., 2008). Some more recent work on the development of experimental electrical underwater manipulators can be found in Pandian and Sakagami (2010) where a three DOF manipulator was developed for validation of control algorithms, Cobos-Guzman et al. (2013)where a three DOF manipulator called LAFMIA-UMI-I was developed which was to be mounted on a mini submarine and Sheikhbahaee et al. (2014) where a four DOF manipulator called Kavosh-4 was developed for usage in towing tank. In Xu et al. (2010) a design for an electrical three DOF manipulator was proposed, which was later developed and tested (Xiao et al., 2011; Shen et al., 2011), and within the RAUVI project, Fernandez et al. (2013) reported modifying a commercially available electric manipulator, ARM 5E, a product of CSIP (now ECA). As a result of collaborative work of IRS-Lab from The Jaume I University in Spain and CSIP company, this manipulator was rebuilt for the purpose of reducing the dimensions and weight so that it can fit on the existing underwater vehicle GIRONA 500 and has less dynamic coupling with it. Another recent custom made electrical underwater manipulator is the UMA (Fig. 8) developed by Graal Tech SRL in Italy for the TRIDENT project and which subsequently is currently commercially available (Ribas et al., 2015). Its unique characteristic is that it is made by modular joints with a compatible electromechanical interface, which allows building a customised manipulator according to the desired user kinematics without doing a dedicated design.
 Fig. 8. Graal Tech UMA, Copyright © 2015 by Graal Tech S.r.l.
Fig. 8. Graal Tech UMA, Copyright © 2015 by Graal Tech S.r.l.4. Commercial underwater manipulator control systems
Commercial underwater manipulators mounted on ROVs are controlled by teleoperation systems and are fully reliant on the pilot/operator in the loop who is located on the surface vessel. The pilot observes the scene through camera and/or sonar systems feedback and simultaneously takes decisions regarding the motion and remotely operates the underwater manipulator using one of a few alternate input devices. Depending on the technical capabilities of the underwater manipulators, different control methods are utilized.
4.1. Rate control
Hydraulic underwater manipulators which are not equipped with position sensors are operated in joint rate (speed) control mode. In this case the motion of manipulator joint actuators is controlled by a valve pack fitted with solenoid directional control valves and/or proportional valves. The most basic control approach with minimum equipment is achieved with directional control valves, often called switching valves because they “switch” the fluid passing through the valve from the source of flow to one of the actuator ports (Walters, 2013) Using a pilot console (Fig. 9) equipped with a set of 3-position ON/OFF/ON switches, the operator controls the valves in the pack and consequently the motion of the manipulator. The size of the valve orifice determines the flow rate of the passing fluid and thus limits the joint speed which can be achieved. The flow rate and thus the actuator/joint speed is regulated (only reduced) to the desired level by additional adjustable flow control valves. Active actuator fluid flow control and therefore joint speed control is achieved by using proportional valves, thus the name proportional control. These valves allow infinite positioning of spools and thus provide infinitely adjustable flow. Some of them are designed to provide directional control functions as well as flow/speed control all in one valve, instead of requiring separate valves for direction and speed. Various required flow rates are achieved by changing the level of electrical signals controlling the valves, and smooth actuator acceleration and deceleration is achieved by regulating rate of change of these electrical signals. The described switch set pilot console is the most basic input device on the pilot side and using it provides the poorest manipulation efficiency. A more sophisticated and intuitive input device that is used is a type of joystick which is often called a rate hand controller or a “bear-claw” (Fig. 10). Some hydraulic control functions are achieved by pushing buttons integrated on this input device and other by twisting it, rocking it from side to side or forth and back. Even though it is more intuitive than the method using a switch set, it still requires quite a skilled and experienced pilot for safe, successful and efficient operation. Such systems utilize no joint sensors and are examples of open loop control systems. Position control is achieved with the pilot in the loop with camera view of the manipulator and scene.
 Fig. 9. Hydro-lek pilot console, Copyright © 2017 by hydro-lek.
Fig. 9. Hydro-lek pilot console, Copyright © 2017 by hydro-lek. Fig. 10. Schilling Rate Hand Controller – ”Bear Claw“, Copyright © 2017 by TechnipFMC plc.
Fig. 10. Schilling Rate Hand Controller – ”Bear Claw“, Copyright © 2017 by TechnipFMC plc.4.2. Position control
Advanced underwater manipulators are equipped with position sensors in each joint such as potentiometers, analog resolvers, digital optical encoders or solid state linear position sensors. In case of hydraulic manipulators, these sensors are used in combination with hydraulic servo valves for the realisation of closed loop manipulator joint position control (set point regulation). Servo valves are electrically operated, continuously acting valves that control how hydraulic fluid is ported to an actuator. Low voltage signals used to control the servo valve are passed into an amplifier which provides the power to alter the valve's position, and the valve then delivers the required fluid power to the actuator (Dunnigan et al., 1996). The position sensor on each joint returns an electrical signal to the servo amplifier which, based on the comparison with the command signal, conditions the strength of the servo valve control voltage. Manipulator joint servo position control is most commonly achieved in a so called master-slave configuration, with the use of a miniature master arm (Fig. 11, Fig. 12, Fig. 13) as an input device with similar kinematics to the slave arm (underwater manipulator). The operator physically manoeuvres the master arm whose motion is then copied to the slave arm, while simultaneously observing the slave arm's response through a video system. Each motion action of the miniature master arm is translated into varying electrical signals by position sensors (usually potentiometers) placed in each joint of the master arm. Simultaneously, position sensors in the slave arm feed back varying electrical signals corresponding to the actual slave arm joint positions. These signals are compared and any difference (error signal) initiates control signals for the servo valve causing it to release a certain flow of fluid to the appropriate port of its hydraulic actuator, resulting in the actuator/slave arm joint moving towards the commanded position. Most master arms have several push buttons integrated for some specific functions. The most common one is “freeze” button which disables the master-slave mode and disconnects the master arm from the control loop leaving the slave arm in the last pose in which it was before the button was pressed. This gives the operator time to rest or reconfigure the master arm pose before continuing with the operation. Other buttons can be used for jaw functions, stowing functions, etc. Master arms are integrated in the master controller which provides additional user interface functions via function keys, display, etc.
 Fig. 11. Kraft master controller, Copyright © 2017 by Kraft TeleRobotics, Inc.
Fig. 11. Kraft master controller, Copyright © 2017 by Kraft TeleRobotics, Inc. Fig. 12. Schilling Master Controller, Copyright © 2017 by TechnipFMC plc.
Fig. 12. Schilling Master Controller, Copyright © 2017 by TechnipFMC plc. Fig. 13. Perry master controller, Copyright © 2017 by Forum energy Technologies.
Fig. 13. Perry master controller, Copyright © 2017 by Forum energy Technologies.4.3. Force feedback
Some master-slave underwater manipulator control systems have force feedback, which enables the pilot to sense reaction forces generated on the underwater manipulator and therefore make remote operation easier and more intuitive. This mode of operation is in literature referred to as bilateral control while the operation without it is unilateral control. In order to provide force feedback, master arms joints are equipped with small electric actuators in addition to position sensors. In the case of hydraulic manipulators, the forces/torques acting on the individual joints of the underwater manipulator are measured either directly, by the use of six axis force/torque sensor located on the wrist of the manipulator, or indirectly, by measuring the pressure in the actuator supply lines and converting this information into a force/torque estimation. In both cases, the force/torque information is then used to condition the strength of the control signals for the electric actuators located in the master arm individual joints, which results in force feedback to the operator. In addition to the improved telepresence, the compliant nature of a force feedback system greatly reduces the risk of accidental damage to both the work site and the manipulator itself. Even with all the benefits provided with force feedback, pilots have to be highly trained in order to successfully operate the subsea manipulator. This is particularly important for the use of manipulators in delicate sites such as archaeological sampling (Søreide and Jasinski, 2008; Scaradozzi et al., 2013). Additionally, if there is a push for resident ROV teleoperation of manipulators i.e. manipulation from shore through network infrastructure, then, again pilot task load is increased and there is a large dependence on pilot skill and network quality. The resident ROV teleoperation concept has recently been introduced in the industry by IKM Subsea where a permanently deployed ROV system is remotely operated from shore (Offshore EngineerM and S, 2016). Chevron adopted a similar field resident concept for AUVs (Gilmour et al., 2012). In the academic sector, the resident ROV concept has been investigated within the DexROV project, and advanced assisted on-shore teleoperation over long distances is proposed (Gancet et al., 2015).
As motion disturbances affecting the underwater vehicle and the manipulator become more significant, the task execution with pilot in the loop becomes more difficult, more time consuming, and eventually impossible, especially in the case where the target infrastructure is in motion and the ROV for some reason, cannot clamp onto to it. The human operator can react only after the change has already happened and therefore even an experienced operator is likely to fail if the conditions for task execution are difficult.
4.4. Gripper control
As is the case for rest of the actuators in the underwater manipulator system, the gripper is also controlled via same miniature master arm in master-slave control mode. The majority of grippers are hydraulically actuated and rate controlled in open loop. The pilot predefines the gripper opening and closing speed in master controller settings and by squeezing the textured bands on the master arm wrist, activates the grip function. Some underwater manipulators have a closed loop servo position controlled gripper which is achieved with sensor feedback, usually a Linear Variable Differential Transformer (LVDT). A minority of suppliers offer grip force control and force feedback.
5. Underwater manipulator motion control
Underwater manipulators are multibody dynamic systems and therefore two main control techniques can be implemented. In the first approach the manipulator is regarded as a mechanical system formed by multiple independent systems determined by the number of joints it has. Each joint axis is controlled individually as a single-input/single-output (SISO) system where coupling effects between the joints, which are induced during the motion due to the varying manipulator configuration, are treated as a disturbance. This type of manipulator control strategy is known in the literature as decentralized control scheme (Siciliano et al., 2009). The opposite strategy is a centralized control scheme which takes dynamic interaction effects between the joints into account for the controller design.
To be able to design an adequate controller for underwater manipulator, some additional factors need to be analysed such as the type of drive system used to actuate manipulator joints.
Manipulators actuated with electric motors usually have high ratio gears which tend to linearise manipulator system dynamics and thus significantly reduce nonlinearity effects caused by coupling effects between the joints. However, this comes at the price of introducing significant joint friction, elasticity and backlash effects. On the other hand, manipulators actuated with direct drives such as hydraulic actuators have to deal with kinematic and dynamic coupling between the joints which is a result of configuration-dependent inertia forces, Coriolis and centrifugal forces. Hydraulic systems introduce high nonlinearities due to laminar and turbulent flow, channel geometry and friction. Additionally, hydraulic system parameters are greatly variable, dependent on the oil viscosityand the relationship between flow and pressure (Yao and Wang, 2012).
Hydrodynamic effects influencing an underwater manipulator such as buoyancy, added mass, dissipative drag and lift forces as well as external disturbances (current, waves, etc.) all add nonlinearities and uncertainties to the dynamics thus making modeling and control even more complicated as the precise estimation of the hydrodynamic coefficients is impossible because they vary according to the temperature, depth, salinity, etc. (Antonelli, 2006). When a body is accelerated through a fluid, some of the surrounding fluid is also accelerated with the body which creates additional inertia added to the system. This is known as the added mass effect and it makes dynamics model parameters become variable and uncertain (Fossen, 2011). Drag and lift forces have a similar influence on the dynamic model parameters. These forces act on a vehicle due to its movement through a viscous fluid and since the density of sea water is significant, the magnitude of these forces can be significant as well. Buoyancy forces work against gravity and are dependent on the density of the fluid and the volume of the fluid displaced by the manipulator (McMillan et al., 1995). Waves, sea currents and tides cause fluid accelerations, and therefore external motion disturbances as well as forced oscillations and loads on the manipulator and the vehicle (Lapierre et al., 1998). Finally, the presence of strong kinematic and dynamics coupling effects can occur between the base vehicle and the underwater manipulator.
Any successful control scheme applied to the underwater manipulator must be able to cope with such highly nonlinear, time varying and uncertain dynamics. There has been an abundance of control schemes proposed for underwater manipulators over more than two decades; however, the majority of research has been done on a theoretical level with control performance validation done through simulations. Some control strategies have been tested on real experimental underwater manipulators but the work done on commercial underwater manipulators is scarce. This is not surprising as the state of the art commercially available manipulators are quite expensive and often have integrated motion controllers with limited access into the control implementation. Any attempt to validate control approaches using commercial manipulators requires a significant amount of modification on the manipulator hardware.
5.1. Decentralized control
Control loop feedback mechanisms which integrate proportional (P), integral (I) and derivative (D) terms in different variations for basic controllers (P, PI, PD, PID, etc.) as a set-point regulators, have been present in industry for decades (Choi and Chung, 2004). Utilizing these PID type control laws for underwater manipulators within a decentralized joint space control strategy offers simplicity of implementation and low computational cost. The trajectory planning for commercial underwater manipulators falls under the joint space point-to-point method (initial to final joint configuration) due to its master-slave teleoperation approach. However, PID based control laws provide poor dynamic accuracy when trajectory tracking comes into play and the dynamic performance of the manipulator varies according to its configuration (Khalil and Dombre, 2004).
Regardless of its limitations, a number of authors including Smith et al. (1994)reported utilizing PID based joint control laws in a decentralized control scheme for underwater manipulators. Dunnigan et al. (1996) incorporated a fixed-gain PID controller for each manipulator joint and realizing that the control performance degrades when the manipulator operates at different points in the workspace, proposed investigating a self-tuning adaptive control approach. The outcome was an adaptive SISO self-tuning pole-placement joint angle controller which provides benefits over a fixed gain PI/PID controller for a range of different operating conditions (Clegg et al., 2001). Ishimi et al. (1991)propose another adaptive PID controller with automatic gain tuning in accordance with arm posture changes and with feedforward compensation for gravity, buoyancy, speed and acceleration. Huo et al. (2013) also analysed the performance disadvantages of traditional PID control and propose a PI algorithm with variable gains. Xu et al. (2005a) utilized fuzzy logic theory for adaptive PD controller gain tuning. Yao and Wang (2012) propose a model reference adaptive control (MRAC) scheme for individual joint control where the interaction between other joints and hydrodynamics influence are considered as external disturbances and controller parameters are adjusted on-line in real time.
5.2. Centralized control
Other authors focused on nonlinear centralized control schemes, which take advantage of the knowledge of an underwater manipulator dynamics model to compensate for the nonlinearities by eliminating them rather than reducing the effect induced by them, and therefore, enhance the trajectory tracking performance (Siciliano et al., 2009).
One of the early works on the investigation of underwater manipulator model-based control is reported in Liceaga-Castro. et al. (Liceaga-Castro et al., 1991) where a nonlinear model matching controller is proposed. The manipulator dynamics model includes some hydrodynamic effects which are calculated according to Morison's equations. Schjølberg and Fossen (1994) derived an underwater manipulator dynamics model with most dominating hydrodynamic forces included using an iterative Newton-Euler algorithm and propose an inverse dynamics control approach. This approach uses a feedback linearisationmethod to completely linearise a nonlinear system leaving it linear and decoupled so that a much simpler stabilizing linear controller can be utilized for trajectory tracking. However, this approach assumes an exact knowledge of the dynamics model which is impossible to measure or estimate. The model is in reality known with a degree of uncertainty and imperfect cancellation of dynamics terms is guaranteed. Therefore, this approach does not have adequate robustness as it is sensitive to time varying and uncertain model parameters and external disturbances (Siciliano et al., 2009).
In order to design a controller that can counteract the effects of imperfect compensation, and thus deal to some extent with variable parameters and disturbances, relaxing the unrealistic assumption of the accurate knowledge of the underwater manipulator dynamics model parameters, some researchers have investigated integrating robust and adaptive control strategies. The former counteracts the effects of the model approximation and the latter adapts the model parameters to those of the real underwater manipulator dynamics model (Siciliano et al., 2009).
Lee and Choi (2000) propose a robust controller designed by combining a computed torque controller and a sliding mode controller (SMC) with a multi-layer neural network controller which acts as a compensator, maintaining the control performance when the initial uncertainty assumptions cease to be valid. Another robust control scheme is presented by Yuh et al. (2001) which consists of a disturbance observer controller, which transforms a nonlinear underwater manipulator system with uncertainties into a simple model with disturbance error, and a non-regressor based adaptive controller designed according to the simplified model. A number of authors propose robust trajectory tracking controllers for underwater manipulators based on the sliding mode controlstrategy and the dynamics model for estimating uncertainty bounds (Kwon et al., 2000; Xu et al., ; Xu et al., 2007). Some authors propose using fuzzy logic heuristics for sliding mode controller adaptive gain tuning (Xu et al., 2005b). An observer-based PD backstepping robust nonlinear control technique for underwater manipulators is proposed by Mohan (2011). Esfahani et al. (2013)presented a control scheme where an artificial immune system algorithm with wavelet mutation is used to derive optimal parameters for the conventional sliding mode controller. A modified sliding mode control scheme, namely terminal SMC is proposed by Venkatesan et al. (2014) with a disturbance observer integrated for dealing with disturbances and uncertainties. Another robust controller with uncertainty/disturbance estimator was presented by Mohan and Kim (2015a), where the proposed controller integrates approximated inverse dynamic model output as a model-base portion of the controller, uses a feed forward term to enhance the control activity, estimates a perturbed term to compensate for the external disturbances and unmodelled dynamics and has a decoupled nonlinear PID as a feedback portion to enhance closed loop stability and account for the estimation error of uncertainties.
5.3. Neural and fuzzy control
Some authors have investigated neural networks and fuzzy logic theory for designing control strategies for resolving the nonlinear control problem without taking into account any knowledge of the underwater manipulator dynamics.
Wang et al. (2008) propose a hybrid control method based on the integration of fuzzy logic control with a cerebellar model articulation controller (neural network). Another fuzzy hybrid control scheme is presented by Suboh et al. (2009) where a Takagi-Sugeno fuzzy controller is merged with a model reference adaptive controller equipped with PI adjustment mechanism based on the previous work of Golea et al. (2002). Pandian and Sakagami (2010)presented a neuro-fuzzy PD control scheme for underwater manipulators where a fuzzy gain tuning method is utilized for adaptation under uncertainties and disturbances while the neural network is used to approximate the dynamics of the underwater manipulator and to add a feedforward compensation input to the PD fuzzy controller.
6. UVMS motion control
Underwater manipulators are usually not standalone systems, but rather a part of a UVMS, as they are mounted on underwater vehicles, in most cases work class ROVs. Work class ROV intervention operations which include using underwater manipulators require at least two highly skilled operators, one to pilot the ROV, trying to keep it as stable as possible by compensating for external motion disturbances (sea current, waves, tides) and ROV motion induced by manipulator's reaction forces/moments, while the other operator performs the actual teleoperated manipulation task. This is the case when the ROV is not operating on the seabed and when there is no possibility to clamp it onto the underwater structure. This can occur if the surrounding environment does not provide adequate conditions for a safe and secure connection or simply if the underwater structure is not designed to be clamped onto. The significant disadvantage of teleoperated control becomes prominent in harsh sea conditions, because even very skilled pilots are able to react only after the disturbance event has already happened, which induces significant delays in the system. Due to a number of handicaps that contribute to the task performance complexity, ROV pilots eventually get fatigued which leads to significant reduction of task effectiveness (Cooke, 2006; Capocci et al. ). Therefore, a plausible approach for solving these problems is to implement semi-automated or fully automated UVMS control methods.
Since underwater vehicle and manipulator motion are coordinated separately, for ROVs in current use, the straight forward approach for UVMS control implementation is to decouple the vehicle and the manipulator and regard the whole system as two independent systems to be controlled. Conventional station keeping algorithms can be utilized for underwater vehicle control while the underwater manipulator motion can be controlled as if it were on a fixed base, having the automated manipulation system carry out the prescribed tasks through arm motion alone. Vehicle position set point can be replanned when the target is out of the workspace of the manipulator. This approach simplifies the manipulator control but places a heavy burden onto the underwater vehicle control system as it needs to have a drive system with sufficient dynamic capabilities and precision navigation, so the overall system can achieve adequate manipulation performance. Research on ROV precision navigation and motion control has been investigated by Toal et al. (2011), Omerdic and Toal (2012) among others, while sole manipulator control algorithms have been outlined in the previous section. The problem of this approach is that it does not take into account the dynamic and kinematic coupling that occurs between the manipulator and its base vehicle, which may significantly degrade the control effectiveness of the whole UVMS. The dynamic coupling arises as the manipulator, while in motion, transmits forces and moments which are variable in magnitude and direction to its base vehicle. These forces and moments alter the pose of the base vehicle and hence the manipulator end-effector position and orientation, which is regarded as kinematic coupling (Dunnigan and Russell, 1994). The factors that cause these coupling effects are the relative size, weight and shape of the manipulator compared to its base vehicle. The lower the manipulator's weight and size compared to the underwater vehicle the better, as coupling can then be either neglected or taken into account and dealt with appropriately. Relative manipulator-to-vehicle weight ratios for the existing typical heavy, medium and light work class ROVs are presented in Table 2. When coupling effect are significant, advanced control approaches have to be adopted.
6.1. ROV compensation for coupling effects
One solution to deal with coupling effects while the manipulator is operating is to decouple the UVMS and run a separate control loop for the base underwater vehicle alone, keeping it in a fixed pose using the propulsion system. This approach was investigated by a number of researchers who proposed advanced station keeping algorithms for the underwater vehicle, taking dynamic and kinematic coupling effects into account.
Koval (1994) proposes an automatic vehicle stabilization method where the manipulator caused vehicle motion is compensated for by feedforward terms based on manipulator kinematics and simplified dynamics (without hydrodynamic forces). Dunnigan and Russell (1994) demonstrated the effect of dynamic coupling between manipulator and ROV through numerical simulations and propose a scheme to reduce it using a variable structure control law where forces/torques affecting the ROV are deduced from the equations of motion which include simplified hydrodynamic terms. McLain et al. (1996)experimentally demonstrated the significance of hydrodynamic coupling between the single-link manipulator and its base vehicle when no vehicle control is applied and described a coordinated control approach for the UVMS by incorporating model-based hydrodynamic coupling information into the vehicle control law.
An alternative approach for ROV stabilization due to the motion induced by an operating manipulator and external disturbances was investigated by Kato and Lane (1995) where multiple smaller arms, other than the main manipulator, were used as paddles for motion compensation.
Interaction forces that occur between the manipulator and its base vehicle can be measured using a six axis force/torque sensor mounted at the base of the manipulator. Some authors propose utilizing controllers for vehicle station keeping that use these measurements in order to compensate for coupling effects by adjusting thruster commands to correct the position of the vehicle (Lapierre et al., 1998; Fraisse et al., 2000).
In case the force/torque sensor is unavailable, Ryu et al. (2001) propose a controller which is based on the developed disturbance observer (Geffard et al., 2000) for the estimation of interaction forces between the ROV and the manipulator. A similar approach is presented by Vossoughi et al. (2004) where forces/moments are estimated based on the dynamic model and used as a feedforward portion of the ROV controller. To predict dynamic coupling forces/torques, Soylu et al. (2005) utilize an articulated-body algorithm (ABA) which is based on the UVMS feedback states, and a sliding mode controller for UVMS station keeping. Using the same ABA algorithm along with a combined H-infinity-Sliding-Mode control scheme for underwater vehicle station keeping is presented by Soylu et al. (2009).
An alternative vehicle stabilization method is proposed by Lynch and Ellery (2014) where the focus is on the control of the UVMS barycenter rather than on the vehicle position. Antonelli and Cataldi (2014) assumed that the manipulator is controlled independently by a joint-based controller and used the information of desired manipulator trajectories to design an adaptive and recursive low level controller for the vehicle. In the ROV case, apart from vehicle-manipulator dynamic coupling effects, hydrodynamic and gravitational forces acting on the tether also create internal forces on the ROV. Soylu et al. (2010a) addressed this problem and performed numerical simulations which revealed the extent to which the tether affects the manipulator dynamics and utilized a model-based sliding mode controller for ROV station keeping capable of dealing with dynamic coupling effects caused by the tether.
6.2. UVMS motion control
Instead of decoupling it into two separate systems, a UVMS can be addressed as a single system which can utilize different control approaches capable of dealing with coupling effects occurring between the manipulator and the base vehicle.
The primary focus for a number of researchers investigating this approach is on the UVMS set-point regulation. Lizarralde et al. (1995) propose a velocity-less PD control set-point regulator which drives the vehicle and the manipulator to the desired attitude and position. Another examples of UVMS set-point regulation is presented by Antonelli and Chiaverini (1998a), where a robust sliding mode based control approach is used, and by Sun and Cheah (2004), with the use of a generalized adaptive saturated proportional-derivative (SP-D) controller with gravity regressor for gravity and buoyancy compensation.
Other authors focused on deriving the detailed UVMS dynamics model and propose the implementation of conventional model-based control schemes which can be applied for trajectory tracking. Utilizing a Newton-Euler approach, Fossen (1991) derived equations of motion for a UVMS considered as a micro-macro manipulator, a specific combination of parallel and serial mechanical structures, where the manipulator gives fast and accurate end-effector motion and the vehicle is the slower positioning part; the same author proposes an adaptive controller for the UVMS, which is based on the work of Slotine and Weiping (1988). Mahesh et al. (1991) derived equations of combined UVMS motion using a vector-dyadic method and designed a coordinated adaptive control strategy where parameters of the linearised coupled model are estimated on-line and used by a discrete-time adaptive velocity controller for self-tuning. McMillan et al., 1995, 1996 report on the developed efficient UVMS dynamics simulation algorithm which includes major hydrodynamic effects which can provide aid in the design of control algorithms. Tarn et al. (1996) use Kane's method for the development of a dynamics model of an underwater vehicle equipped with an n-DOF manipulator including major hydrodynamic terms as well, and thus provide a good background for the design of UVMS control algorithms.
Schjølberg and Fossen (1994) propose a feedback linearisation approach followed by a derivation of the detailed dynamic model including the most important hydrodynamic terms. A similar approach based on feedback linearisation has been investigated by a number of other researchers. Schjølberg and Egeland (1996) utilize two different spacecraft-manipulator system control schemes and apply them on the UVMS; Tarn and Yang (1997) address a multiple manipulator UVMS model which includes major hydrodynamic forces; Wilson et al. (2011) have developed a computed torque controller for UVMS; Mohan (2013) present a model reference UVMS control scheme and Korkmaz et al. (2013) present an inverse dynamics control method for UVMS trajectory tracking where separate tasks are assigned for the end-effector and the vehicle. Mohan and Kim (2012) propose a nonlinear control scheme based on the feedback linearisation using indirect knowledge of the system dynamics and external disturbances via an extended Kalman filter. The same authors in (Mohan and Kim, 2015b) propose a coordinated motion control scheme using a disturbance observer in task space. Londhe et al. (2017) propose a Robust Single Input Fuzzy Logic Controller (RSIFLC) applied for task-space trajectory controlthat consists of feedback linearisation and feed-forward controllers along with a single input fuzzy controller and an uncertainty estimator.
The main drawback of the feedback linearisation approach is that it assumes the exact knowledge of the system dynamics or at least a close estimation which is unrealistic and does not guarantee robustness to model parameter variation and uncertainties. Dunnigan and Russell (1998) emphasize the significance of dynamic coupling through computer simulations on a six DOF vehicle equipped with a three DOF manipulator and integrate closed form manipulator disturbance expressions neglecting hydrodynamic terms into a sliding controller which is capable of dealing with parameter uncertainties to some extent. In order to improve dynamic coupling modeling accuracy and achieve better UVMS coordinated motion control, Leabourne and Rock (1998)present research on an empirically determined hydrodynamic manipulator model, acquired by real experiments with a two-link manipulator mounted on a free floating vehicle. De Wit et al. (De Wit et al., 1998a) emphasize that manipulator-to-vehicle coupling effects are dominant over the vehicle-to-manipulator ones and that the feedback compensation is only needed to overcome the coupling effects from the manipulator. The UVMS is divided into two subsystems, one of which is fully independent from the other (manipulator) while the other (vehicle) is perturbed by the first subsystem (manipulator). An approach based on a singular perturbation is proposed, as alternative to existing approaches requiring full model knowledge to compensate for vehicle/manipulator coupling and their nonlinear effects, by a partial linearising decoupled controller. Based on the same decoupling approach, De Wit et al. (De Wit et al., 1998b) present a robust non model-based controller for the UVMS which consists of a linear PD controller for the manipulator and a robust nonlinear controller for the underwater vehicle based on the work reported by Williamson and De Wit (Williamson and De Wit, 1995). A comparative study of the proposed controller neglecting previous assumptions such as that the saturation levels of thrusters are unbounded, infinitely accurate sensors, infinitely small sampling time and absence of thruster nonlinearities is presented by Diaz et al. (1998). Based on the same singular perturbed model, De Wit et al. (De Wit et al., 2000) propose a robust nonlinear feedback control for the UVMS with composite dynamics, which offers good compromise between control complexity and closed-loop performance.
A modular approach for UVMS control is presented by Antonelli et al., 1999a, 2004 where an adaptive tracking controller with virtual decomposition (Zhu et al., 1997) is adopted. The proposed control approach exploits the serial-chain structure of the UVMS to decompose the overall motion control problem into separate simple rigid body control problems, i.e. manipulator links and the vehicle. Sarkar and Podder (2001) use a quasi-Lagrange method in order to derive UVMS dynamic equations of motion which include thruster dynamics, and utilize a computed torque control law for UVMS trajectory tracking. Unlike most control methods based on the computed torque, Ishitsuka et al. (2004)propose a resolved acceleration control (RAC) method for the UVMS. The proposed control method is verified by numerical simulations reported by Ishitsuka and Ishii, 2005, 2006. An extension of this algorithm which includes compensation for disturbances caused by hydrodynamic forces acting on the vehicle along with the experimental verification can be found in Yatoh and Sagara (2008). Sagara et al. (2010) present another addition to the algorithm where the disturbance compensation is utilized both for the vehicle and the manipulator followed with the experimental validation. Finally, the same method is enriched for a dual manipulator control scheme (Sagara and Ambar, 2014). Xu et al. (2005c) present a non-adaptive model-based sliding mode controller for UVMS based on the decentralized dynamics with simulation validations showing that the proposed sliding mode controller provides accurate and robust tracking performance, superior to that obtained with a traditional PD controller. Periasamy et al. (2008) present the development of a UVMS dynamic model using the bond graph modeling technique where major hydrodynamic effects and coupled dynamics are included and they have designed a PD plus buoyancy compensation control for the UVMS end-effector trajectory tracking. Han et al. (2011) proposed a robust UVMS control approach where a nonlinear H-infinity optimal control is utilized as an external tracking control loop and a disturbance observer as an internal disturbance compensation loop.
During the execution of the UVMS intervention task, the manipulator motion causes the shift of the orientation equilibrium of the whole UVMS, which causes restoring moments and forces to change as well and this eventually leads to additional spontaneous end-effector motion. In order to exploit this phenomenon, Han and Chung (2014) proposed a robust adaptive control scheme that uses variant restoring moments to actively control the UVMS.
Most of the existing UVMS control approaches neglect the existence of nonlinear thruster dynamics. Taira et al. (2010) present a regressor-based adaptive controller for UVMS with thruster dynamics where adaptive control inputs are composed of adaptive feedforward signals including regressors of dynamic system models and error feedback signals. In order to simplify the complex structure due to regressors, the same authors propose an adaptive controller in Taira et al. (2012) that uses radial basis function (RBF) networks (Haykin, 1998) instead of the regressors, while in Taira et al. (2011) they propose a robust controller where the feedforward term is removed completely. The performance of the robust controller is improved with pre-compensators including integral actions (Taira et al., 2014).
In order to avoid the unrealistic assumption of exact knowledge of UVMS dynamics and the complexity of estimating close to the real dynamic model, some authors resorted to adaptive control methods that are independent of any model knowledge. Lee and Yuh (1999), Lee et al. (2000) report on a non-regressor based adaptive control scheme for UVMS trajectory tracking based on a bound estimation method and a parameter adaptation algorithm for adjusting the controller gains based on the performance of the system rather than the knowledge of the dynamic model. A sliding mode type controller with fuzzy logic implementation for adaptive gain tuning is proposed by Xu et al. (2005b). Using fuzzy logic heuristics for decentralized proportional derivative (PD) type controller gain tuning is also presented in Xu et al. (2005a). Sakagami (2009)propose using an iterative learning control approach in order to deal with the manipulator-to-vehicle coupling effects which assumes that the motion of the manipulator that is to be compensated for is known in advance.
6.3. Manipulator compensation for coupling effects
Some authors address the end-effector trajectory tracking control problem of UVMS in a different manner where the focus is on developing advanced manipulator control methods which alone compensate for the movement introduced by coupling effects between underwater vehicle and manipulator and/or the external disturbances.
One of the early references to compensation of the underwater vehicle motion as a result of external (tidal) disturbances is by Ishimi et al. (1991), where a sway compensation controller is developed which uses the inertial navigation system (INS) signal, transforms it into a displacement of the manipulator and adds it to the position command signal as a feedforward term, thus cancelling out the sway of the vehicle with manipulator motion alone. Chung et al. (2000)propose modeling a UVMS as a class of underactuated robotic system with the assumption that the vehicle is free floating and proposed a robust control algorithm where the ROV is modelled as a passive joint and manipulator joints are modelled as active joints. A robust control method is realized with a nonlinear feedback disturbance observer plus PD control scheme and applied to each active joint. Kim et al. (2003) propose an active damping two-time scale control approach where the vehicle is passive or controlled by a simple P-type controller and the manipulator is controlled with a composite two-time scale (fast and slow) controller designed according to a partial decoupling approach. An algorithm implemented on the manipulator system that is able to actively compensate for the ROV motion based on the model based vehicle motion prediction algorithm is proposed by Hildebrandt et al. (2009b).
Some authors have investigated compensation schemes such that the manipulator control law is a function of the vehicle velocity. In the TRIDENT project, Simetti et al. (2014) propose a dynamic programming (DP) approach which allows an optimal manipulator movement based on the current measured vehicle velocity. Simetti et al. (2017) report experimental results of the MARIS project including a parallel task-priority inverse kinematics (TPIK) solution for manipulator control also based on vehicle velocity.
Some authors propose using vehicle motion to complement the capabilities of the manipulator by providing extra DOFs to achieve manipulator end-effector trajectory tracking, rather than having the underwater vehicle passive or controlled for station keeping (Antonelli et al., 2000, 2004; Antonelli and Chiaverini, 2003a, 2003b). However, using thrusters for manipulator end-effector positioning is inefficient from an energy consumption perspective. This is due to the complexity of controlling the underwater vehicle in hovering and lateral directions as well as because of significant difference in vehicle and manipulator inertias (Mohan et al., 2012).
7. Kinematic control and motion planning
In order to improve the overall performance of underwater manipulation, many researchers utilized kinematic level enhancements. Some focus on the improvement of conventional pilot teleoperation techniques while others resort to the utilization of semi-autonomous and fully autonomous control techniques in the hope of transferring the operator from direct control to a supervisory position. Some of the early research on teleoperation control enhancements includes the development of a human-machine interface where a choice of possible remote control input devices is available, including keyboard, mouse, master arm or joystick, each of which provides benefits for different tasks (Larkum and Broome, 1994). Another important approach that has been investigated by many researchers includes real time motion simulations and virtual graphical reconstruction of the manipulator workspace including workpiece solid models presented on the monitor display. Such tools provide supplementary visual aids in the traditional teleoperation by helping the operator to perceive the posture of the underwater manipulator and possibly avoid collision with the environment. Relevant pioneering research on this topic is reported by Ishimi et al. (1991), Broome et al. (1995), while more recent research work can be found in Zhang et al. (2003), Hildebrandt et al. (2008a), Jun et al. (2009). The description of the implementation in further detail can be found in the previous paper (Sivčev et al., 2015), published by the authors.
A number of researchers have investigated Cartesian space teleoperation schemes as such an approach is more intuitive from the human perspective, and advantages that it offers for various underwater manipulation tasks are quite clear, especially for the “peg-in-a-hole” type tasks. Operational space teleoperation techniques implemented and tested on work class ROV have been reported in Jun et al., 2004, 2008, 2009. A workspace control approach which is based on the implementation of the differential inverse kinematics algorithm is developed where the operator uses an input device to control the manipulator end-effector velocity and hence its position and orientation in Cartesian space. Hildebrandt et al. (2008b) presented optimal direct kinematics and closed-form analytical inverse kinematics solutions with special respect to computational simplicity whilst maintaining high numerical precision. This has been applied to control a commercial underwater manipulator, a Schilling Orion 7P. Fernandez et al. (2013) also address Cartesian space control with implementation on a modified version of the ECA ARM 5E. Huo et al. (2013)utilize an analytical inverse kinematics solution for the six DOF underwater manipulator developed by the Shenyang Institute of Automation of the Chinese Academy of Sciences, and the authors, Sivčev et al. (2015), present a numerical method for the solving inverse kinematics problem for a commercial underwater manipulator, Schilling Titan 2, as finding the closed form analytical solution for the specific manipulator is impossible due to the lack of a spherical wrist (Siciliano et al., 2009). A Cartesian space teleoperation approach which offers a variety of reference coordinate systems such as joint, world, and tool is demonstrated on a simulated model in virtual reality and in subsea trials (Sivčev et al., 2018a). Implementing inverse kinematics algorithms and developing Cartesian control methods opens a lot of new possibilities for semi-automated supervisory control schemes and fully-automated manipulation solutions. In the former the operator selects a task via user interface and then observes and monitors while the task is being executed, while in the latter the task is sensor triggered. Moreover, this approach brings underwater manipulation closer to totally automated industrial (terrestrial) robotics (Sivčev et al., 2015). This is due to the fact that the majority of industrial robot arms have kinematics control (end-effector motion trajectory planning) carried out in the operational (Cartesian) space, followed by inverse kinematics implementation and finally low level motion control (motion trajectory tracking control) performed in the joint space. On the other side, commercial underwater manipulators are teleoperated and therefore kinematics set point control is carried out in joint space since the master arm motion is recorded in joint space and then copied directly to the slave arm.
One of the earliest references on the implementation of supervisory control for underwater manipulators is by Ishimi et al. (1991) who describe how after an operator has chosen a task, motion planning is utilized automatically based on the knowledge of the environment, work tools, platform, etc., and then transformed into data for manipulator motion control. Broome et al. (1995) also discuss semi-automatic and fully automatic modes backed up with motion planning algorithms and inverse kinematics implementation. Zhang et al. (2003) propose a semi-autonomous manipulator control under operator's supervision with a possibility of using a visualization display as a tool for outlining tasks. Jun et al. (2009) present a preprogramed way point task control approach where the manipulator is able to execute a task for which a path was taught by the operator in advance. The efficiency of this approach has been experimentally tested on ROV mounted Schilling Orion 7P manipulators performing a soil coring task.
Hildebrandt et al. (2008a) propose integrating additional features to the online virtual reality 3D visualization that could help the operator during the supervisory control such as visualization of end-effector paths or previewing possible manipulator configurations prior to the actual movement as a result of motion planning algorithms. This is achieved by a secondary 3D visualization of the manipulator projected as a semi-transparent overlay. Another feature that can aid the pilot in teleoperated mode is proposed by Albiez et al. (2009) based on the workspace analysis of the manipulator, where a computer is continuously calculating the distance to the workspace border, enabling the operator to get information about current dexterity of the underwater manipulator, the ranges where the dexterity does not exceed a given limit and the possibility for automatic motion.
Some authors propose integrating collision avoidance algorithms into supervisory and totally autonomous control schemes (Broome et al., 1995). Ishibashi et al., 2001, 2002 use genetic algorithms for obstacle avoidance of both stationary and dynamic objects where both position of the end-effector and posture of the manipulator is utilized for motion planning. David et al. (2007) propose integrating an active collision avoidance feature based on the MARGRITTE 3D graphic supervisor (Gravez et al., 2003) into the enhanced teleoperation scheme by coupling the real robot manipulator with a simulated one to generate movement for both of them. Since the simulated manipulator has integrated algorithm for automatic obstacle avoidance in the virtual reality the operator can handle the real slave manipulator safely without taking care of real environment obstacles, assuming perfect knowledge and modeling of obstacles. This control scheme was developed for use in the nuclear environment but was tested on a Cybernetix Maestro hydraulic underwater manipulator which could be applied for subsea applications. Sivčev et al. (2018b) propose a voxel based collision detection algorithm applicable for commercial work-class ROVs.
Some authors address kinematic control and motion planning algorithms on a UVMS level. Podder and Sarkar (2000) propose a dynamics-based trajectory planning approach capable of generating both kinematically admissible and dynamically feasible joint space trajectories for systems composed of heterogeneous dynamics such as UVMS, characterised by a much slower dynamic response of the underwater vehicle compared to that of the manipulator. In the proposed approach, task-space trajectory is represented in terms of Fourier series and various frequency components from the series are used to generate reference joint-space trajectories based on natural frequencies of the respective subsystems. Shim et al. (2013) address UVMS motion planing and control based on ROV position estimation using extended Kalman filter and propose a precise dynamic workspace control method where the manipulator is controlled to move in a straight line while the ROV is assumed to be floating. A method for UVMS global motion planning, capable of generating feasible and obstacle free task paths based on the 4D bump surface concept is presented by Sotiropoulos et al. (2013). The PANDORA project has explored learning the trajectory of the vehicle and the end-effector by demonstration (Carrera et al., 2014) to accomplish the valve turning, with experiments in a tank environment. In the MERBOTS project Youakim et al. (2017) have used the motion planning ROS package MoveIt! to compute reference trajectories for the UVMS. Advanced control problems considering dual arm UVMS are presented in (Farivarnejad and Moosavian, 2014; Simetti and Casalino, 2015; Ambar et al., 2015). Even more complex problems, such as cooperative UVMS are addressed in (Conti et al., 2015; Simetti and Casalino, 2017). Ocean One project developed a bimanual force controlled “humanoid” robot that affords immediate and intuitive hapticinteraction in oceanic environments (Khatib et al., 2016).