Parameter extraction techniques for the analysis and modeling of resistive memories

1. Introduction

Memristive devices [[1], [2], [3]] are under scrutiny by the scientific community due to their potential in applications of most interest in the electronics landscape, such as non-volatile memory ICs [[4], [5], [6], [7]], neuromorphic computing [[8], [9], [10], [11], [12], [13], [14], [15], [16], [17], [18]] and hardware cryptography [[19], [20], [21], [22]]. There are several types of memristive devices whose operation mechanisms are strongly linked to their geometry, and the dielectric and electrode materials employed in their fabrication [[4], [5], [6], [7],23,24]. For instance, Phase Change Memories [25], which are based on the behavior of phase change materials that can be switched reversibly between amorphous and crystalline phases of different electrical resistivity; Magnetic RAMs [26], that use magnetic and electrical properties exhibited by some materials in particular structures; Ferroelectric devices [27], whose properties are linked to materials with switchable electrical polarization that produce hysteresis curves of the polarization versus electrical field and can be engineered for storing information; finally, the devices with more versatility, Resistive Random Access Memories (RRAMs), where the conduction is linked to internal ion movement and concurrent redox reactions in the dielectric and dielectric/electrode interfaces, which can be used to generate different resistive states in a digital and analog perspective [[28], [29], [30]]. This manuscript will concentrate on the latter group of devices, RRAMs (also known as resistive memories); in particular, in the extraction procedures that allow obtaining parameters to characterize the resistive switching (RS) operation and the models used to describe the charge conduction features.

Resistive memories have shown outstanding endurance [31] behavior, good retention and low power operation. These devices present a compact crossbar structure (4F2 footprint, where “F” is the minimum technology half-pitch) that is compatible with CMOS technology and low power operation [5]. These devices are being employed as non-volatile memories in commercial fabrication processes. For instance, in the 22 nm node, the following companies incorporate RRAMs: TSMC [32] and INTEL [33]. For this work, we will take into consideration two different types of redox-based devices: electro-chemical metallization cells [23] (also known as conductive bridge RAMs, CBRAMs) and valence change memories (VCMs) [29,34].

We will present here general extraction methodologies for resistive switching parameters. These techniques could work better in one type of device than in others, depending on the operation features and the corresponding current-voltage (I-V) curve shapes that can be obtained both in the quasi-static and transient regimes. In this respect, we account for the fact that there is a wide variety of RRAMs, as different electrodes and dielectrics can be used. Transition metal oxides [[35], [36], [37], [38], [39], [40]] are usually employed, although 2D materials such as graphene oxide [41] or h-BN [21] can also be incorporated. These material associations could lead to filamentary conduction where RS is linked to the formation and rupture of conductive filaments. That is, the set and reset processes that lead to the low resistance state (LRS) and the high resistance state (HRS) are associated to the formation and destruction of CFs that short the electrodes leading to a localized ohmic conduction regime. Other devices show area-dependent conduction that could be attributed to the following conduction mechanisms [29]: Schottky barrier limited transport, where the conduction limiting contact is found at the electronically active electrode; Space Charge Limited Current with a non-exponential voltage dependence that is sometimes employed to explain valence change memories (VCM) cells transport; or Poole-Frenkel conduction where a current process based on trapped charges takes place and the electrons are transported over the dielectric conduction band to the electrode, etc.

Compact models for resistive memories are needed for IC developments. In this field there are open issues such as a good modeling of device-to-device and cycle-to-cycle variability [[42], [43], [44], [45], [46], [47], [48], [49], [50]], thermal effects [[51], [52], [53], [54], [55], [56], [57]], and models accounting for second-order memristors [51,58], even third-order ones [59], etc. Electronic design automation (EDA) tools need the implementation of these compact models for circuit simulation. In addition to the model development efforts, the parameters of these models for each technology have to be determined; in this respect, parameter extraction methodologies are needed. At this point we contextualize this review in which we bring most of the different techniques developed for the extraction of some parameters in resistive memories under one roof [2,[60], [61], [62], [63], [64]]. In this context, the particularities of the experimental current data that cover several orders of magnitude in the transition from the HRS to LRS and the other way around, the limitations of the measurement equipment, device noise, etc., have to be dealt with the appropriate mathematical techniques [23,48,50,60,63,[65], [66], [67]]. Revision works on parameter extraction techniques for other types of devices (e.g. FET devices) can be found in the literature [[68], [69], [70]]; nevertheless, as far as we know, this has not been done yet for resistive memories.

We will also show detailed device simulations to shed light on the RS operation and assess the appropriateness of the proposed numerical techniques for parameter extraction. We will make use of kinetic Monte Carlo (kMC) simulations [44,47,53,[71], [72], [73], [74]] both for the unipolar [71,75] and bipolar [53,76] devices under consideration in this work; although, other types of simulators [37,56] could also be used.

2. Device fabrication and measurement set-up

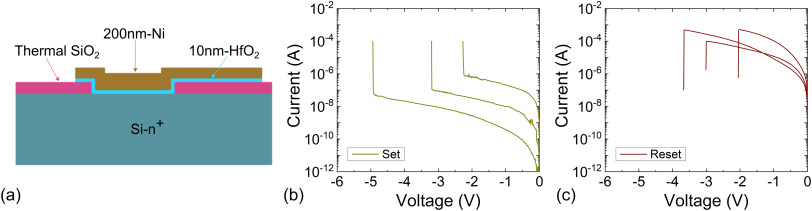
The electrochemical metallization (ECM) cells employed in our study are based on the unipolar Ni/HfO2/Si stack. They were fabricated on (100) n-type CZ silicon wafers with resistivity (0.007–0.013) Ω cm. The hafnium oxide layerswere 10 nm thick and were grown by atomic layer deposition at 200°C using tetrakis (Dimethylamido)‑hafnium (TDMAH) and H2O as precursors, and N2 as carrier and purge gas. More details are available in Ref. [77]. A schematic cross-section of the final device structure is shown in Fig. 1a. The current-voltage curves were measured under ramped voltage stress (RVS) using a HP-4155B semiconductor parameter analyser (SPA). The voltage signal was applied to the top Ni electrode, the Si substrate was grounded. The SPA was connected to the computer via GPIB and controlled using MATLAB. 300 I-V curves were obtained in a RS series with consecutive set and reset cycles after a forming process with a compliance current (ICC) of 0.1 mA. Some of the set and reset curves are shown in Fig. 1b and c.

The bipolar VCM devices were built using the TiN/Ti/HfO2/W stack [34]. They were fabricated on a highly-doped N-type (ρ = 4 mΩ·cm) silicon wafer. The top metal electrode is a (200 nm TiN/10 nm Ti) bi-layer, and the 50 nm-thick W bottom electrode was deposited on a 20 nm-thick Ti adherence layer on the silicon substrate. The 10 nm-thick HfO2 dielectric layer was grown by ALD, see the device layer structure in Fig. 2a. For electrically contacting the W bottom electrode through the highly-doped N-type Si substrate, a 500 nm Al layer was deposited on the back of the wafer by magnetron sputtering. More details are given in Ref. [78]. The ICC was fixed to 10 mA. Again, 300 I-V curves were measured under RVS (Fig. 2b). The RS cycles were programmed with a Matlab software tool that controls a Keysight B1500A SPA via GPIB.

3. Set and reset voltage extraction methods

In this section, we focus on the extraction procedures to obtain the set and reset voltages. These parameters are essential to characterize the transition from the HRS to LRS and the other way around (see Fig. 3). Most papers devoted to experimental RRAMs extract these parameters, although many of them do not clearly state the methodology to do so. As it will be shown below, the numerical technique used for the extraction is linked to the obtained device variability; because of that, the methodological description should be always given.

The great variety of technologies employed for RRAM fabrication produces different I-V curve shapes; some devices can even show unipolar behavior both at positive and negative voltages. Consequently, not all the methodologies presented here fit well for all the different technologies, although they can be adapted in most cases. We will discuss it throughout the manuscript. These extraction techniques work correctly for the devices under consideration here.

See in Fig. 3 that once the set or reset voltages are obtained, the corresponding currents at those values are assumed to be the set and reset currents. From the modeling viewpoint, the set and reset voltages can be useful in behavioral models, where functions such as the hysteron are employed to model the hysteresis loops which could describe well the transitions from LRS to HRS and vice versa, that are inherent to the RS operation [79].

We will consider here I-V curves obtained under ramped voltage stress, the usual characterization procedure for RS operation. The extraction techniques are, therefore, used for these RVS data; however, they could also work well for pulse voltage stress (PVS) operation with none or slight modifications.

3.1. Set voltage extraction

The set process drives the device from the HRS to the LRS. If the conduction is filamentary, one or several CFs are formed that bridge the electrodes. Some of the extraction procedures for the set voltage are given below and they are applied to the two different technologies employed here, i.e., for the ECM and VCM devices described in Section 2.

3.1.1. Maximum current derivative determination (MS1)

The MS1 method is based on the current derivative determination by employing a five-point numerical technique, see Fig. 4 for an example in the unipolar devices under consideration.

This methodology is particularly appropriate for I-V curves with a sudden current rise at the set point, as it is the case for our ECM devices. However, in some curves this technique could lead to the last point of the curve if it is limited by ICC. In this case we could have to choose the point prior to the one corresponding to ICC or the antepenultimate. Other technologies give rise to more complex set curves, such as in the bipolar devices case (Fig. 5). The current derivative is also useful to obtain the set voltage in this case, although the extraction is not that clear. That is why we limit the voltage range where the methodology is applied (in our case located in the [0, 0.7 V] interval), in order to avoid the onward region where random curve shape modifications could generate derivative values leading to an erroneous extraction [80].

3.1.2. Current increase in two consecutive points (MS2)

Another conventional methodology employed consist in detecting a certain current increase in two consecutive points (Vset = Vi if Ii+1 ≥ (1 + a)Ii) [56].

We employed a = 1 and a = 2 for the unipolar devices (Fig. 6a). Note that higher a parameter values work better assuming the sudden current rise that takes place at the set point. An a = 1 value could lead to error in some curves (Vset1 in Fig. 6a) if a non-fully realized set processes is found; however, for higher values, a ≥ 1.5 the real set voltage (Vset2 in Fig. 6a) can be detected. If the a parameter value is too high, it will lead to an undetected set voltage, therefore, a tuning process is necessary for each technology.

For the bipolar devices, commonly, a parameter values in the [0.3, 0.4] interval work well. Nevertheless, the results for a = 0.3 are not correct (Vset1 in Fig. 6b). But for a ≥ 0.4 good results are obtained (Vset2 in Fig. 6b). Therefore, a fitting process is needed for the whole data set obtained in the RS series, since the a parameters are constant for the whole RS series. This methodology also works for technologies different from the ones evaluated here as shown in Ref. [56]. Finally, we call the reader's attention to the fact that the a parameter choice could be connected with the voltage step employed in the measurements and the applied voltage ramp rate. This issue has to be considered in the a parameter fitting process.

3.1.3. Maximum separation from a straight line that joins the first and end points in a set curve (MS3)

The technique MS3 was developed in Ref. [80]. It is based on finding the maximum separation of the measured curve to an imaginary straight line that joins the first point measured at null voltage and the first point when the compliance current is reached (Fig. 7). Our main pursue here is the determination of the set curve knee (see Fig. 7). The experimental curve is shown from the beginning of the measurement (VApplied = 0 V) till the end of the voltage ramp. Then, the greatest distance, dmax, between the experimental curve and the straight line determines the set voltage Vset (Fig. 7).

The whole set of results of the techniques described above are shown in Fig. 8for the two technologies we are considering. The cumulative distribution functions (CDF) are plotted versus voltage, this is a common manner to evaluate cycle-to-cycle variability. It can be seen that the measured C2C variability depends on the extraction technique, as shown in [80].

The lower variability corresponds to the MS3 technique. The calculation of the coefficient of variation (CV, ratio of the standard deviation to mean) allows a quantitative description of variability, see Table 1. In the bipolar devices, a slightly higher variability is obtained in the MS1 with respect to MS3, this latter result could be connected to the variations linked to the derivative calculation and the I-V curve shape; nevertheless, in the unipolar case, since the maximum derivative is clearly found at the end of the set point, MS1 and MS3 are similar in terms of the CV and the corresponding CDFs overlap. The higher variability is obtained for the MS2 method, and as it would be expected, it depends on the a parameter. The variations in the formation of the conductive filaments that facilitate resistive switching operation produce current changes along the I-V curve (as the set and reset processes evolve) and these effects could lead to the changes that come out from method MS2 for different a parameters.

Table 1. Mean, standard deviation and coefficient of variation (ratio of the standard deviation to the mean) for the devices under study in the set case. All the methods discussed above have been considered.

Method	MS1	MS2a	MS2b	MS3	MS1	MS2a	MS2b	MS3
Empty Cell	Ni/HfO2/Si-n+ devices				TiN/Ti/HfO2/W devices
Mean, μ (V)	3.05	2.36	2.64	3.04	0.47	0.34	0.36	0.41
Standard deviation, σ (V)	0.56	0.67	0.61	0.56	0.05	0.06	0.07	0.04
Coefficient of variation	0.18	0.28	0.23	0.18	0.11	0.19	0.18	0.10

3.2. Reset voltage extraction

The reset process increases the device resistance from the LRS to the HRS. In case of filamentary conduction, the CFs that short the electrodes are destroyed, and the dielectric high resistivity is partially recovered. The different numerical techniques for the reset voltage determination can be linked to the stages of CF rupture that the device undergoes in the reset process [56], although this is not an easy task due to the inherent stochasticity of RS operation. Kinetic Monte Carlo simulations can be used to deepen on the RS dynamics as it will be shown below. In addition, advanced statistical techniques, such as these based on phase-type distributions, can be employed to characterize the CF destruction stages along a reset process [62,67,81,82].

The most representative extraction techniques for the reset parameters are described below. As in the previous section, we will employ both the ECM and VCM devices under consideration here.

3.2.1. Minimum current derivative determination (MR1)

The technique MR1 uses the current derivative determination by employing a five-point numerical differentiation to extract the reset voltage and current. An example is given in Fig. 9 for the bipolar devices, see that the minimum derivative occurs at the region where the more pronounced current decrease is found, as expected. For this technology, the technique works well even though there are other curve sections where the current drop takes place because of the inherent device stochasticity.

As can be seen in Fig. 1c, the abrupt current drop that takes place in the unipolar devices at the end of the I-V allows an easy determination of the reset voltage using this technique. Even in the case of current jumps along the I-V curve, the higher derivative is clearly found at the end of the curve, corresponding to the CF rupture.

3.2.2. Current decrease in two consecutive points (MR2)

A decrease in two current consecutive points can be used to extract the reset voltage (Vreset = Vi if Ii+1 ≤ (1 + a)Ii) [56,80]. As in the case of the set voltage determination, the a parameters that work well depend on the particular RRAM technology.

For both type of devices under consideration here we have employed a = 0.05 and a = 0.1 to assess the different reset voltages extracted. The a = 0.05 case is not good enough to circumvent the usual RS current variations in a I-V curve for the unipolar devices; therefore, a = 0.1 was chosen. See that the expected results are then reached in this latter case (Fig. 10a). A trade-off is needed for each technology since a very high a parameter could prevent the obtention of any reset voltage along the I-V curve. As highlighted above, the measurement features such as the voltage step and the applied voltage ramp rate have to be taken into account since the election of the a parameter could be linked to them.

3.2.3. Determination of the current maximum (MR3)

This methodology has been employed previously in Refs. [80, 83]. It is an interesting technique since no indeterminations are produced in most cases. It works well for many technologies, including the two we are assuming here, see Fig. 11, Fig. 12.

Although the current drop in the bipolar devices is not as abrupt as in the unipolar case, this MR3 technique works well. Note that, as shown in the inset in Fig. 12, this method could lead us to detect wrong reset voltages at high voltages. Because of this, for this VCM technology, the interval to check this condition is limited from 30% to 80% of the voltage variation range.

3.2.4. First point with decreasing current (MR4)

This technique was proposed in [56]. It allows to build a robust algorithm, although it is much more sensitive to RS current jumps than the previous ones. In here (Fig. 13) a simple two-points formula is employed for the derivative calculation since we are just interested in the first negative derivative value.

The use of this technique in our bipolar devices produces also different results from MR1, as can be seen in Fig. 14.

3.2.5. Null charge derivative in the charge-flux domain (MR5)

If we represent the experimental I-V curves in the charge-flux domain [2,65,84] (see the Appendix), a simple representation is obtained (Fig. 15). If we perform the charge derivative with respect to the flux and detect when this derivative is null, a new methodology for the reset voltage determination comes up by means of determining the (Qreset, ϕreset) values [61].

This method must be modified for bipolar devices since the Q-ϕ curves are different from those obtained for ECM devices. For bipolar devices (Fig. 16) there is no saturation of the Q value, and correspondingly no null Q-ϕ derivatives; in this respect, we use the maximum charge derivative decrease along the curve to obtain the (Qreset, ϕreset) pairs that allow the calculate the reset voltage.

Taking into consideration all the methodologies described above for the reset voltage extraction, we were able to obtain the CDFs, see Fig. 17.