1. Introduction
The environmental issues, such as global warming, sea-level rising and climate change, caused by the burning of fossil fuels have become more and more serious since industrial revolution. There is an urgent need to develop sustainable and clean energy for powering the low carbon future of the planet. Among the available renewable resources, solar energy is the most abundant inexhaustible energy to humankind. Besides, photovoltaic (PV) technology has experienced enormous growth and PV system has achieved world-wide acceptance over the past few decades. Land shortage is another problem of many coastal cities as nearly 40 percent of the world’s population live within 100 km of the coast (UN, 2017). Considering the fact that over two third of the earth’s surface is covered by ocean, ocean space utilization could be a good solution to release the land-use pressure. Combining with the development of solar energy, a promising option to tackle both the land and energy problem is to develop offshore floating photovoltaics (OFPV). The idea of OFPV is to install PV systems on seawater and not occupy land space.
OFPV technology is generally a combination of PV technology and the floating technology. Even though flexible OFPV has been proposed as cost-competitive concept and has recently been developed in nearshore, there is still a long way to go for commercial floating technology that can take kilometer size structures into rough offshore environments. The floating technology for OFPV requires that the structures have enough buoyancy to float themselves as well as the PV panels and are able to withstand strong wind, wave, and current loads in open seas. Additionally, proper mooring systems are needed to keep the system in place. Moreover, the efficiency and economic potentials in synergies of offshore solar and offshore wind as well as aquacultures indicated that OFPV plants are better constructed in combination with other marine systems (López et al., 2020, Zheng et al., 2020).
The challenges for the development of floating technology for OFPV are the determination of (1) structural deformations under harsh wave conditions, (2) the acting wave forces on the structures in the regime of strong hydroelastic interaction, and (3) the surrounding wave responses due to the existence of the structures.
OFPV is an emerging field of research and development in recent years, see e.g. Jamalludin et al. (2019), and many different structural concepts are proposed as support structures. Based on inland floating solar systems, which are primarily pontoon-based (Trapani and Santafé, 2015, Sahu et al., 2016), modular floating designs are extended to offshore applications, such as the projects of Oceans of Energy (2019) and the tank tests of connected triangular pontoons of Waals et al. (2018) and Otto et al. (2020). However, modular structures cause limitation on the size of plant and cannot withstand extreme environmental conditions as there will be large stress concentrations on the connection elements (Oliveira-Pinto and Stokkermans, 2020). Alternatively, a flexible floating system consisting of thin-film PV arrays was designed by Trapani et al. (2013) with focus on large-scale offshore solar development. Trapani’s concept was based on a thin floating polymer layer with length and width of 600 m 200 m. Compared to the pontoon-based type, the flexible approach is more commercially attractive due to the inherent flexibility allowing the system to easily deform with wave motions, leading to low wave forces acting on the structure and the moorings. This economic advantage of flexible floating support was also mentioned in the project of Ocean Sun (2018), where pre-stretched membranes of several millimeters thin are used for mounting rigid PV panels. More recently, Solar@Sea I & II test showed the potential of floating, non-rigid thin-film PV modules for large-scale PV installations (Soppe, 2020). The continuous flexible system is suitable for utility-scale structures of square kilometer in size—either as a single structure or in a combination of modules.
Considering flexible support for OFPV, Schreier and Jacobi (2020) conducted experiments with a very flexible floating sheet subjected to regular waves. They found that their flexible sheet mainly followed the local wave elevation and the vertical deflections were large compared to the structure thickness, which was different from the motion of VLFS and sea-ice where deflections were mostly in the same order of the thickness.
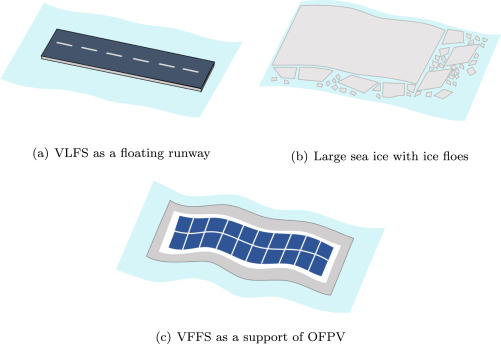
Structures with square kilometer in horizontal size have been studied before for floating runway Mega-Float (Suzuki, 2005) and in sea-ice research. The newly proposed structures have much smaller thickness to horizontal dimensions ratio, leading to low bending stiffness in the vertical direction, and thus making the structure very flexible under wave actions. Fig. 1 illustrates the concept of VLFS, sea ice, and VFFS.
With very large horizontal dimensions compared to their structural thickness, there are parallels between flexible floating structures for OFPV support and pontoon-type VLFS (Wang and Tay, 2011) as well as sea-ice (Squire, 2008). According to Suzuki et al. (2006), elastic deformation are the governing response of those structures in waves.
 Fig. 1. Concept sketch of VLFS, sea ice, and VFFS.
Fig. 1. Concept sketch of VLFS, sea ice, and VFFS.There are currently not many investigations available regarding very flexible support systems for OFPV. Therefore, based on the similarities between flexible OFPV structures and VLFS and sea-ice, numerical and experimental studies were reviewed in this paper to assess the applicability of employed theories as well as experimental and numerical techniques to these newly proposed structures. The analytical consideration of the hydro-elastic problem is described in Section 2. The review of previous works is presented in Section 3. Section 4 analyses the previous work and gives a characterization of the investigated structures. The applicability of the available theory is discussed in Section 5, and concluding remarks are given in Section 6.
2. Analytical consideration of the hydro-elastic response
Compared to other marine structures, VLFS and sea ice have two distinct hydrodynamic features. One feature is that the structures have large horizontal dimensions of several kilometers and rather small vertical size of only a few meters, thus resulting in very small bending rigidity in vertical direction. The other one is that the wavelengths of practical interest are small compared to the structure length. These two features make the elastic behavior more important than rigid body motion (Suzuki et al., 2006).
2.1. Analytical models
Due to their large horizontal dimensions and a small vertical one, VLFS and sea ice are often regarded as mat-like structure resting on water surface and modeled as a thin elastic plate with zero thickness. The hydro-elastic problem is usually simplified to be a linear problem by assuming both the incident wave amplitude and the structure displacement are small. The classic thin plate theory (also known as Kirchhoff plate theory) is thus being used to describe the vibration of the floating body. The governing equation is given as (1)where is the vector differential operator defined as ; is the plate rigidity with Young’s modulus, cross-sectional area moment of inertia per unit width and Poisson’s ratio; is the mass per unit area of the plate; is the density of the fluid; is the gravitational acceleration; is the dynamic pressure on the bottom surface of the plate. The pressure relates to the velocity potential at the bottom surface of the plate by (2)and is the complex vertical displacement of the plate satisfying the boundary condition at the bottom surface of the plate by (3)
For simplicity, considering an elastic floating body with zero-draft subjected to linear regular wave, and assuming all motions are time-harmonic with the common time dependence applied to all first order oscillatory quantities, the velocity potential becomes , and the first order vertical displacement of the plate becomes , where represents the real value; is the imaginary unit; the angular frequency; and the time. Substituting Eqs. (2), (3) into Eq. (1), and factoring all quantities by , the governing equation then becomes (4)This equation can be seen as a modified free surface boundary condition with consideration of floating plate properties that are different from water waves. When and , it becomes the free surface condition of open water wave.
2.2. Hydro-elastic dispersion relation
From the modified free surface condition, i.e. Eq. (4), the dispersion relation of elastic waves of a thin plate can be expressed as (Ohmatsu, 2005) (5)or an alternative form (6)where is the water depth, is the heave natural frequency of the dry plate, represents the hydro-elastic wave number and represents the characteristic wave number of the plate.
If and , Eq. (5) or Eq. (6) becomes the dispersion relation of open water wave (7)
In case of wave propagating to a floating plate with and , the hydro-elastic wave number is theoretically determined by term .
When , i.e. , the hydro-elastic wave number is equal to the open water wave number : . The hydro-elastic wavelength is the same as the propagating wavelength.
When , i.e. , the hydro-elastic wave number is larger than the open water wave number : . The hydro-elastic wavelength is thus shortened by the elastic floating structure.
When , i.e. , the hydro-elastic wave number is smaller than the open water wave number : . The hydro-elastic wavelength is thus lengthened by the elastic floating structure.
As the wave energy should be continuous at the side of the structure, the change in wavelength underneath the structure would result in the direction of wave celerity changing accordingly, as shown in Fig. 2. Physically speaking, when wave shortens, the outside wave would enter into the hydro-elastic zone which causes wave focusing, whereas wave lengthens, the wave would exit from the hydro-elastic zone which causes wave spreading. Note that wave shortening could cause unexpected large deformation of the structure due to wave energy increases beneath.
 Fig. 2. Schematic of wave focusing (green) and spreading (red) . (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Fig. 2. Schematic of wave focusing (green) and spreading (red) . (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)2.3. Structural stiffness
As shown in Eq. (6), is an important parameter to quantify the effect of structural bending stiffness on hydro-elastic response. In this study, for the purpose of an intuitive comparison to the length scales, the characteristic length instead of is used. was firstly proposed by Suzuki and Yoshida (1996) and the equation was given in Eq. (8) by Suzuki et al. (2006)based on beam results. (8)here is the bending stiffness of the beam per unit width. The product is the hydro-static stiffness of structure per unit width. The is the characteristic length of the elastically supported beam and can be interpreted as the length affected by a localized load. Suzuki et al. (1997) defines VLFS not only as floating structures with large horizontal dimensions compared to wavelength of practical interest, but also as having lengths larger than the characteristic length.
For comparison purposes, plate and beam structures were characterized by , where the plate bending stiffness is converted to and the characteristic length of a plate is expressed as .
3. Review of VLFS and sea ice studies
Floating technology has received significant attention among industry and research as VLFS have been foreseen as promising alternatives to relieve the vigorously growing pressure on land use for population accommodation and industrial expansion (Wang and Tay, 2011; Lamas-Pardo et al., 2015). However, although the concept of VLFS has been introduced over 100 years ago and the floating technology has achieved great improvement since the 1990s, real VLFS are still yet to come due to their distinct structure size and the complex interaction with waves. To predict the hydro-elastic response of these structures in waves, many analytical or numerical, and experimental studies have been carried out over the past few decades. In this section, the common methods used to solve the wave–structure coupled equation (Eq. (1)) are firstly outlined, the numerical and experimental studies in VLFS and sea-ice are then reviewed.
3.1. Numerical studies
As shown in Eq. (1), the motion of the structure is governed by a fourth-order partial differential equation, the analytical solutions of these equations are essentially impossible to achieve except in some one-dimensional cases. Alternatively, numerical studies are used and developed along the evolution of floating technology. Over the decades, different numerical approaches to the hydro-elastic problem have been proposed and a variety of structures have been investigated.
3.1.1. Hydroelastic methods
Pioneering work of hydroelasticity theory was done by Bishop et al. (1979) and Mei and Tuck (1980) for 2-dimensional model and Wu (1984) for 3-dimensional analysis. Early applications of hydroelastic theory to large floating structures include Langen and Sigbjörnsson (1980) and Georgiadis (1981) for “beam-like” structures as well as Price and Wu (1985) and Wu and Du (1990) for complex structures of arbitrary geometry.
Regarding the nature of solution in the structure, a decision must be made by choosing a method in one of two broad categories (Ohmatsu, 2005). The first set of option is the modal expansion method. In this method, the structure motion and the hydrodynamics are solved separately. The structure motion is approximated by a summation of the product of modal functions and their complex amplitudes, while the hydrodynamic part can be obtained through Green’s integral method or eigenfunction expansion-matching method. The coupling is then achieved by evaluating the hydrodynamic forces on the structure for unit amplitude motions of each mode. The second family is the so-called direct method, in which the velocity potential is directly obtained by solving the coupled equation of motion without the help of modes and the structure motion is then estimated from the resultant potential.
Using modal expansion method to solve hydroelastic problem has a very long history, early full description of this method can be found in the work of Bishop et al. (1979) and Wu (1984). Later, as VLFS received high interest among industry and academia, modal expansion method was widely used in the hydrodynamic analysis of beam-like or pontoon-type VLFS due to its simplicity of determining motion vibration (Wu et al., 1995, Wu et al., 1996, Kashiwagi, 1997, Kashiwagi, 1998a, Hermans, 2000, Abul-Azm and Gesraha, 2000, Meylan, 2002, Andrianov, 2005, Montiel, 2012, Karmakar and Soares, 2012, Praveen et al., 2018, Praveen et al., 2020). Along the development of this method, various types of modal functions have been proposed, including modes of a finite free–free beam (Gran, 1992, Newman, 1994, Maeda et al., 1995, Taylor and Ohkusu, 2000), finite plate with free edges (Meylan and Squire, 1996, Meylan, 2002), infinite or semi-infinite beam and plate (Hermans, 2000, Andrianov, 2005), and B-spline functions (Kashiwagi, 1997, Kashiwagi, 1998a). The modes may be of the dry type considering structure vibration in vacuum or wet type including the fluid effect on the modes shapes calculation (Taylor, 2003, Loukogeorgaki et al., 2012). Most researchers used the dry-mode approach because these modes are easily specified in advance by applying the orthogonality properties.
In the line of direct method, early procedures developed by Mamidipudi and Webster (1994) and Yago (1997) using Green’s function of the water surface to solve the wave components and the finite difference/element scheme to obtain the structure motion were shown to be time and memory consuming for the calculation of wave interaction with a large floating structure. To avoid those disadvantages, Ohkusu and Nanba (1996) introduced a different direct method for pontoon-type VLFS based on the analytical approach of sea ice proposed by Evans and Davies (1968) and Meylan and Squire (1994). The idea of this approach is to treat the floating structure as part of the water surface but with different physical properties, thus replacing the structure mechanics problem of determining the elastic motion of the body due to wave actions by a boundary-value problem in hydrodynamics. The Green’s function of the floating cover is used rather than that of the free water surface. To reduce the computation time of Green’s function integration over the wet surface of the structure, Ertekin and Kim (1998) proposed an efficient expansion matching approach based on the direct method by using eigenfunctions of the wave to estimate the velocity potential rather than integrating Green’s function of the structure over the entire wet surface. They showed that their approach is efficient for parametric study of hydroelastic response of pontoon-type VLFS because the discretizationof the structure was needed only along its edges rather than on the entire pontoon in usual panel methods, replacing the time-consuming evaluation of the area integral by efficient line integrals. Kim and Ertekin (2000) and Hong et al. (2003) modified this approach by accounting for finite draft effect on the structure behavior.
Comparison work of modal expansion method and the direct method was done by Taylor (2007). Results showed that the modal expansion method overestimated the effect of hydrodynamic forces but it was more lucid and time-efficient in computation than the direct method, but for large and flexible structures, massive numbers of modes might be needed. Additionally, calculations of wave quantities was not straightforward in modal expansion method. Moreover, the direct method avoids the error induced by truncating the series expansion of the modal expansion method. However, the direct method leads to much larger system of unknowns and for high frequency motions, the expression of Green’s function of the structure was badly conditioned, limiting the application of the approach to comparatively stiff structures, like ice floes. Hegarty and Squire (2008) further points out that the method based on Green’s function of the structure did not converge to higher-order deflections. The pros and cons of the hydroelastic methods are summarized in Table 1
Across the modal expansion method and the direct method, the hydro-elastic problem is addressed by boundary element method (BEM) finite element method (FEM), or the hybrid BEM-FEM. In general, BEM traditionally gained a degree of popularity on a basis of efficiency. Because in BEM the partial differential equations are formulated as integral equations using Green’s function method and the given boundary conditions of the problem are used to fit the boundary values into the integrals, rather than values throughout the space. Therefore, only the surface, rather than the entire volume, needs to be discretized in simulation, which leads to the reduction of spatial dimensions of the problem by one, and a smaller system of equations in the computation program. Particularly, BEM is well-suited to problems with infinite or semi-infinite domain (see e.g. Hermans, 2000, Andrianov and Hermans, 2006). Whereas in FEM, problem domain of interest is divided into collection of finite sub-domains (finite elements) and the concept is to represent the geometry of each single sub-domain by applying proper boundary conditions and loads. A variety of different finite element formulations has been proposed over the years to modal problems of various complexity.
Table 1. Overview of pros and cons of hydroelastic methods.
| Method | Pros | Cons |
|---|---|---|
|
Modal expansion method |
–lucid procedure –time and memory efficient |
–overestimates hydrodynamic forces –many modes needed for large and very flexible structures –prone to modes truncation error |
| Direct method |
–straightforward calculation –no modes truncation error |
–large number of unknowns –badly conditioned Green’s function in very flexible structures –convergence problem in higher- order deflections |
However, due to volume discretization in FEM, the system of equations could be considerably large due to the higher number of degrees of freedom in the system. Besides, FEM can be very computationally expensive as the stability of FEM is highly dependent on the mesh quality, a very fine mesh is required for accurate prediction. By contrast, there are far less elements in BEM because of surface discretization. Although BEM gives full matrices whereas FEM leads to narrow brand ones, a full BEM matrix usually still solves faster than a sparse FEM matrix. One major limitation of BEM is its less successful application to nonlinear problems (Wu and Taylor, 2003), but higher-order BEM (HOBEM) could be an option (Heo and Kashiwagi, 2019, Heo and Kashiwagi, 2020).
To make use of the advantages of BEM and FEM, a hybrid BEM-FEM technique has been developed in which the BEM is used to discretize the fluid field and FEM is used to discretize the floating structure. Early BEM-FEM procedure applied in VLFS can refer to e.g. Utsunomiya et al., 1995, Yasuzawa, 1996, Yago, 1997 and Hamamoto et al. (1997). Further improvement to higher-order BEM-FEM approach respecting computational efficiency and accuracy has been continuously proposed in the field of hydroelasticity (e.g. Kashiwagi, 1998c, Wang and Meylan, 2004, Yoon et al., 2014, Shirkol and Nasar, 2018, Shirkol and Nasar, 2019) .
3.1.2. Application of hydroelastic method
Modal expansion method has been used extensively over the past decades. Wu et al. (1995) conducted a 2-dimensional analysis of an experimental model of 10 m by 0.5 m by 0.038 m with m. The structure motion was estimated by the free–free beam modes proposed by Newman’s (Newman, 1994). The wave field was approximated by wave eigenfunctions. This solution is also called the eigenfunction expansion-matching method (EEMM). Acceptable agreement of the calculated displacement and bending moment results with experimental values was obtained. Then Wu et al. (1996) extended the application of the modal expansion method to 3-dimensional box-like pontoons with dimensions of 300 m by 60 m by 2 m and 4000 m by 1250 m by 4.5 m. The wave field was solved by using the water surface Green’s function. Comparisons between 2-dimensional results and 3-dimensional results indicated that the 2-dimensional approach overestimated the global response and for short wavelengths, where the 3-dimensional analysis was recommended. Kashiwagi (1997) applied the modal expansion method with cubic B-spline functions on a floating elastic plate of 5000 m long, 1000 m wide and 5 m thick with a characteristic length of 782 m in the regime of very short wavelengths. Satisfactory results were obtained up to , with feasible computation time and the number of unknowns for routine use. Ohmatsu (1997) investigated the hydroelastic behavior of typical VLFS with various lengths ranging from 1200 m to 4800 m subjected to rather short waves using EEMM. Chen et al. (2003) used modal expansion method with Green’s integrals to address the large-amplitude response problem of a pontoon-type VLFS treated as a floating plate of 300 m 60 m 2 m with m in monochromatic and multi-directional waves. Worth noting that in this work, they provided a nonlinear hydroelastic solution that accounted for geometric characteristics of the structure in short waves using Föppl–von Kármán plate theory. Detailed description of the problem solution accounting for the geometric nonliterary can be found in Chen et al. (2004). The nonlinear membrane forces induced by large deflections were calculated. Comparison between linear and nonlinear results indicated that membrane forces had little effect on the motion response, but increased the longitudinal stress by 30% in the case of monochromatic waves. Watanabe et al. (2006) proposed a benchmark analysis of circular VLFS using modal expansion method. Radius of 50 m and 200 m with thickness 5 m and 2 m were considered in their work. Response of deflection, bending moment, twisting moment and transverse shear force were calculated. Gao et al. (2011) addressed the hydroelastic problem of a hinged thick VLFS by applying the modal expansion method to the structure and the boundary element to the fluid domain. Tay and Wang (2012)conducted a numerical investigation of floating plates of 300 m by 60 m by 2 m and 150 m by 150 m by 2 m with various fore- and aft-end shapes in regular waves using modal expansion method with boundary integrals. More recent, the application of the modal expansion method can be found in motion prediction of various complicated floating structures proposed to meet different engineering needs, such as modular VLFS (Yang et al., 2019, Ding et al., 2020), VLFS with different support conditions (Praveen et al., 2019), floating VLFS with submerged plates (Mohapatra and Guedes Soares, 2016, Mohapatra and Soares, 2019), VLFS with anti-motion device (Cheng et al., 2016, Singla et al., 2019, Pu and Lu, 2022), circular flexible VLFS (Heo and Kashiwagi, 2020, Meylan, 2021). Wave interaction with sea ice shares the same fundamental mathematical model with wave-VLFS interaction (Squire, 2008). Modal expansion method can be also applied to the hydroelastic analysis of wave–ice coupling problem, such as Meylan (2002), in which the wave-induced motion of a flexible ice floe of rectangular, diamond, trapezoid and triangular shape was calculated based on modes approximation method. But for wave propagation through ice floes, multiple ice floes should be considered. For hydroelasticity of multiple ice floes, the wave scattering between the ice floes should be included, modal expansion method may not be a good choice since it has a drawback of estimating wave scattering. Here we keep our focus on continuous structures so multiple ice floes are omitted. The reader is referred to the latest overview by Squire (2020)for multi-structure models of ice-related research.
For the direct method, the early application on hydroelastic analysis can be found in the problem of wave–ice coupling (Evans and Davies, 1968, Meylan and Squire, 1994). Meylan and Squire (1996) investigated the hydroelastic response of circular ice floes represented by circular disks to long-crested ocean waves using the direct method, in which Green’s function of the ice cover was adopted. Their models had various radii from 50 m to 400 m and a constant thickness of 0.5 m with a characteristic length of 57.1 m. To improve the computational efficiency of the direct method, Athanassoulis and Belibassakis (1999) proposed a coupled-mode method to address the coupling equation by introducing the series expansion of wave field into variational principle rather than using the integral approach. Belibassakis and Athanassoulis (2005)addresses the hydroelastic problem of large floating structures over different bathymetry conditions using a coupled-mode model. Studies on the hydroelastic response of a 500 m long floating ice sheets with small draught and variable thicknesses in different slopping bathymetry conditions were conducted in the work of Belibassakis and Athanassoulis (2005) and Belibassakis et al. (2013). In VLFS study, based on the idea of treating the floating structure as part of the water surface but with different physical characteristics, Ohkusu and Nanba (1996) extended the application of method proposed by Meylan and Squire (1994) to wave-VLFS study. Ertekin and Kim (1999) analyzed the hydroelastic response of a 5000 m by 1000 m by 5 m floating runway in regular, oblique, shallow water waves by the direct method. Effects of stiffness, structure length and width on structure deflections, wave reflection and transmission were discussed. Ohkusu and Namba (2004) studied the bending vibration of a large thin floating plate of 5000 m by 1000 m by 5 m with a characteristic length of 420 m in monochromatic waves of 100 m to 250 m long using the direct method. However, Green’s function of the structure is badly conditioned for higher-order deflections and high frequency motions limiting the application of the direct method to relatively stiff structures. For more complicated cases of wave floating structures interaction, the most popular solution is BEM-FEM, such as Yoon et al., 2014, Lu et al., 2016, Shirkol and Nasar, 2019, Luong et al., 2020, Nguyen et al., 2020 and Jiang et al. (2021).
An overview table of VLFS numerical models is provided in Table 2. Because for large ice structure simulations, infinite or semi-infinite models were usually used and the thickness information was often not given, it is difficult to generate the overview table of numerical ice research in the same pattern of Table 2. Hence the table of numerical ice models is omitted.
Table 2. Models used in VLFS simulations.
| Reference | |||
|---|---|---|---|
| Wu et al. (1996) | |||
| Wu et al. (1996) | |||
| 338 | Ohmatsu (1997) | ||
| 782 | Kashiwagi (1997) | ||
| 418 | Ertekin and Kim (1999) | ||
| 288 | Ertekin and Kim (1999) | ||
| 418 | Hong et al. (2003) | ||
| 188 | 50.0 | Chen et al. (2003) | |
| 420 | Ohkusu and Namba (2004) | ||
| R 50 × 5 | 287 | 50.0 | Watanabe et al. (2006) |
| R 200 × 2 | 181 | 50.0 | Watanabe et al. (2006) |
| 188 | Gao et al. (2011) | ||
| 188 | Tay and Wang (2012) | ||
| 188 | Yoon et al. (2014) | ||
| 304 | – | Cheng et al. (2016) | |
| 188 | Lu et al. (2016) | ||
| R 1 | – | Heo and Kashiwagi (2020) | |
| R 2 (dimensionless) | 2.09 | Meylan (2021) |
R: the radius of the structure.
3.2. Experimental studies
In analytical or numerical prediction, assumptions made to make the problem calculable may ignore some important physics, and the predicted results may be different from the actual cases. It is therefore crucial to conduct experiments of elastic floating structures to validate the theoretical analysis and also investigate the structure behavior in real conditions.
3.2.1. Law of similarity
In practice, full-scale structure experiments on large floating structures are generally not possible, so model-scale structures are alternatively used. Reasonable conversion from results of model-scale structure to results of full-scale structure can be achieved by satisfying the similarity law. In linear regime, the motion of full structure and experimental model should satisfy the equation of motion (Eq. (1)) and the dispersion relation (Eq. (6)). For a floating structure with a very large horizontal size and a rather small vertical one, elastic body motion is dominant in the structure behavior (Suzuki et al., 2006). Hence bending rigidity similarity between the model and the actual structure is necessary to be considered. Ohmatsu (2008) gives the list of similarity conditions related to the hydro-elastic response of VLFS based on the derivation results of Endo (1991). Among them, the parameters of similarity in Table 3 are important in VLFS experiments.
However, it is often very difficult to satisfy the similarity law of bending rigidity in VLFS. Because if only consider the geometric scaling, the rigidity per unit width in the model by definition is scaled by which does not match with the result derived from the equation of motion, where the rigidity should be scaled by . Therefore, different materials and fabricating methods have to be used to simultaneously satisfy the similarity condition of mass and bending rigidity between model-scale structures and full-scale structures (Ohmatsu, 2008).