Highlights

•
A comprehensive review of machine learning-based solar stills is presented.
•
The bibliometric analysis of the topic is conducted.
•
Principles and the mathematical description of common models is given.
•
Various investigated solar still designs and machine learning significance are illustrated and compared.
•
Advantages and limitations of the models are highlighted.

Abstract

Being a cheap, simple, and low-energy consumer, solar stills have been introduced by water and energy scientists as an alternative desalination method to fossil fuel-based ones. A wide variety of designs and modifications have been applied to enhance the solar stills' performance, which may be associated with experimental works that require time and cost. Therefore, coupling solar stills with state-of-the-art machine learning is expected to overcome these disadvantages of experimental work. Artificial intelligence models try to build relationships between the input and output data similar to the human brains depending on given dataset. In light of these, this paper carries out a literature review that considers the applications of artificial intelligence in solar stills’ performance prediction. It covers the most repeated machine learning methodsemployed for performance prediction, focusing on principles, advantages, limitations, and the mathematical description of each method; besides the models' evaluation criteria. Then, comprehensive discussions are performed on the solar stills models by classifying them according to the design. The work compares the previous studies within comprehensive analyses that give reasons for the authors' findings, highlighting the reasons for the variation between the models' prediction and experimental findings. Accordingly, models with root mean square errors close to zero are highlighted throughout the review.

Keywords

Solar still

Machine learning

Performance prediction

Optimization

Modeling

1. Introduction

The freshwater shortage is a critical challenge worldwide as the demand for freshwater for drinking and personal use has increased rapidly following population growth [[1], [2], [3]]. Hence, the World Health Organization declared that freshwater shortage suffering is expected by 2025 [4,5] as it is anticipated that water demand will rise by about 65 % in the period between 2020 and 2025, according to Leon et al. [6]. In the past decades, desalination methods such as multi-stage flashing [[7], [8], [9], [10], [11]], multi-effect evaporation [[12], [13], [14]], and single-effect evaporation [[15], [16], [17]] were commonly used for freshwater production in the arid regions and the Arab Gulf States [18,19]. However, this solution raised another challenge since these methods are high-energy consumer methods that cannot be practical in the current energy crises [20,21]. Accordingly, in recent years, renewable energy-based desalination methods attracted the attention of the water and energy science community, who are seeking to develop desalination methods with high water production capacity, low cost, and only depend on renewable energy sources[[22], [23], [24], [25], [26]].

Solar still (SS) is a renewable energy-based desalination method that only uses solar energy with a very simple design, only a basin for containing the water and glass cover to allow the solar rays penetration [[27], [28], [29], [30]]. Its method applies the principle of evaporation and condensation since solar energy carries out the evaporation process, and the vapor condenses on the SS's glass cover. Such simple operating principle and structure resulted in low water productivity [31,32]. Therefore, SS technology passed through many designs and modifications, all seeking higher distillate productivity [[33], [34], [35]]. The SS's performance improvement can be accomplished by assisting the evaporation process or boosting the condensation process. For the evaporation process, techniques like nanofluids [[36], [37], [38], [39], [40], [41], [42], [43]], thin film [[44], [45], [46], [47], [48], [49]], thermal storage [[50], [51], [52], [53]], waste bottles [54], metal chips [55], corrugated basins [[56], [57], [58]], reflectors [[59], [60], [61]], solar collectors [[62], [63], [64]], and foggers [[65], [66], [67]] all of them try to find a way to reduce the thermal inertia for faster evaporation or increase the received energy for the same purpose. For the condensation process, glass cover cooling [[68], [69], [70]] and external condensers [71,72] are the most common methods; both seek a faster condensation process. On the other hand, the development of SS's structure tries to increase the condensation surface area (glass cover), which in turn would enhance the condensation procedure. Besides, increasing the transparent area allows extra solar energy receiving and reduces the shade cast on the water, then better evaporation process [73,74]. Several studies have concerned the thermoeconomic and thermoenviroeconomic performances in terms of energetic and exergetic performance, cost, and environmental analyses to evaluate the significance of the proposed modifications [75,76].

This diversity in designs and modifications is associated with time and money costly experimental work. Since it is required to spend several days of testing in order to establish a single modification [76,77]. Therefore, coupling SS with state-of-the-art machine learning is expected to minimize the dependency on the experimental work by using artificial intelligent models for performance prediction. This method tries to build relationships between the input and output data similar to the human brain as it only requires an established dataset of inputs and inputs. After training the model by the experimental dataset it becomes able to predict the results by giving only the input data [78,79]. In other meaning, neither experimental work nor mathematical models would be required to evaluate the SS's performance.

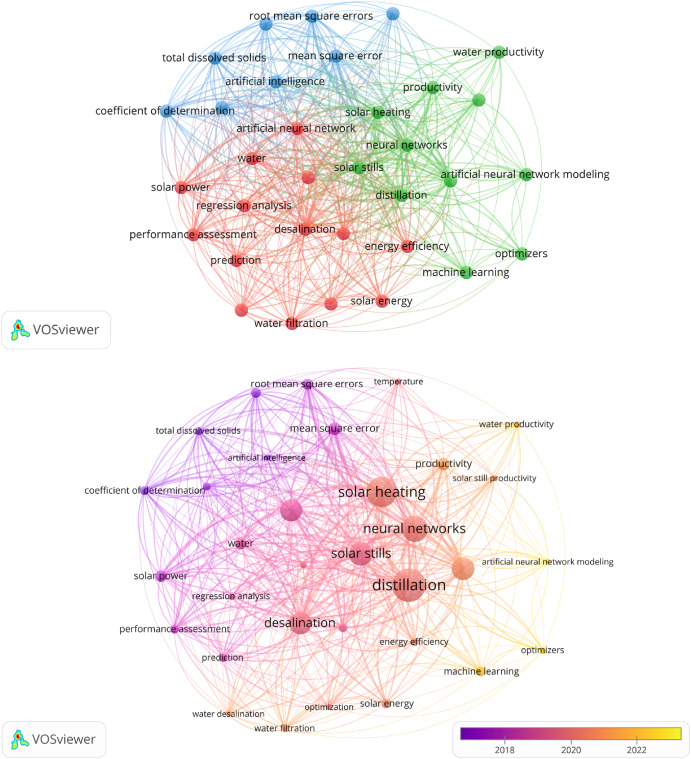
The research trend in the topic of SSs coupled with machine learning models is justified via a bibliometric analysis depending on the Scops database. For this function, the Vos viewer tool was employed to manage the Scopus database results with a keywords arrangement set as ({Solar still} OR {Solar distiller}) AND ({Machine learning} OR ({Artificial neural network} OR {Artificial intelligence})). The analysis is conducted regarding indexed and authors keywords co-occurrence, authors and countries' contributions, and journals coupling, all depending on 51 documents within the last ten years.

Indexed keywords co-occurrence represents the data in three color groups Fig. 1(a). The blue group highlights keywords like root mean square error, mean square error, and coefficient of determination. In other words, the blue group represents the documents that were interested in model assessment and error detection. Similarly, the red group contains keywords that deal with energy and solar still as keywords like solar power, solar energy, performance assessment, and desalination, while a few words associated with the modeling appeared for instance, prediction and artificial neural network. Hence, the red group can be described as a group that focuses on solar stills and the modeling is an additional function. However, the green group is otherwise where it used keywords linked to machine learning. Keywords like machine learning, optimizers, artificial neural network modeling, and neural networks. Still, a wide range of keywords linked to solar appear in the green group. Accordingly, the green group is a group that contains comprehensive studies that were interested in the models and solar stills. Indexed keywords co-occurrence based on the data of publications shows that the green group is the most recent group Fig. 1(b). The red group came second, and the blue group was the last group for the modernity perspective. Considering these, model assessment started first; then, the models were combined with solar still as a second function. Accordingly, the most recent studies adopted machine learning in their study in wide ranges.

In this context, some review papers presented machine learning methods' application in solar energy and desalination. Attar et al. [80] published a review article that presented the utilization of machine learning models in solar radiation forecasting. Elsheikh et al. [79] focused on the machine learning model applications in solar energy-based systems. He et al. [81] reviewed desalination methods’ performance prediction via machine learning models. Rashidi et al. [82] performed another general review study that considered solar desalination methods modeling via artificial intelligence. Moreover, Vakili and Salehi [83] introduced a specified review paper that considered only the solar collectors associated with machine learning.

This paper, according to the best knowledge of the authors, introduces the first specified literature review that considers the applications of artificial intelligence in solar stills' performance prediction. This review work aims to give a complete picture of this hot topic. To achieve this objective, the most common machine learning methods that are repeatedly utilized in predicting the SSs' performance are introduced in detail. The models' discussions include their principles, advantages, limitations, and mathematical description. Then, the statistical criteria that are often applied to evaluate the prediction accuracy of the models are given. On the other side, the survey gives a comprehensive description of the SSs' thermal assessment formulas with their physical and mathematical meaning. Beyond these overviews, comprehensive analyses and illustrations are performed on the SS's models by classifying the SS's according to their structural shape. Furthermore, the contributions and limitations of each model are being surveyed through the work.

2. Description of machine learning models

2.1. Multilayer perceptron neural network

The multilayer perceptron (MLP) method attempts to find relationships between the output and input neurons which is inspired by the human brain. It consists of an input layer, an output layer, and multiple hidden layers. Numerous neurons make up each layer [52]. Moreover, the input layer's neurons are linked to those of the next hidden layer, and the hidden layer's neurons are linked to those of the output layer [53]. Stated differently, information is moved from the receiving layer (input layer) to the hidden layer and finally to the output layer. Each neuron is linked to each neuron in the previous and following layer, while the neurons are not connected to each other in the same layer Fig. 6. For an input layer with M neurons, the output neuron $O_{1, k_{1}}$ is obtained as follows:(1) $O_{1, k_{1}} = f (\sum_{m = 0}^{M} w_{m k_{1}} x_{m}), k_{1} = 1, \dots, K_{1}$ where, $k_{1}$ -th and $x_{i}$ are the receivers and the input, respectively. The output is later employed as an input of the next layer which is generally a hidden layer. Then, the hidden layer output ( $O_{h, k_{h}}$ ) is modeled as follows:(2) $O_{h, k_{h}} = φ (\sum_{K_{h - 1} = 0}^{K_{h - 1}} w_{k_{h - 1}, k_{h}} O_{h - 1, k_{h - 1}}), k_{h} = 2, \dots, K_{h}, h = 1, \dots, N_{h}$ where, $k_{h} = 1, \dots, K_{h}$ denote the hidden layers. $φ (.)$ is the activation function. $w_{0, k_{h}}$ stands for the input basis function. It gives the weights between the neurons in the hidden and input layers. $N_{h}$ and $K_{h}$ demonstrate the number of the hidden layers, and $h$ is the neurons of the hidden layer. Then, the final output ( $y_{l}$ ) is obtained as follows:(3) $y_{l} = \sum_{k_{N} = 0}^{K_{N}} w_{k_{N}, l} O_{N, k_{N}}, l = 1, \dots, L$ where, $w_{k_{N}, l}$ gives the weights joining the neurons in the output and hidden layer. $L$ denotes the number of output layer neurons.

2.2. Radial basis function

The MLP method and the radial basis function (RBF) approach are nearly identical in that both involve many hidden layers in addition to an input layer and an output layer. Also, for RBF, multiple neurons make up each layer [57]. Similarly, as shown in Fig. 7, the neurons of the input layer are linked to those of the next hidden layer, and the hidden layer's neurons are linked to those of the output layer. In other words, the data is transferred from the input, receiving layer, to the hidden layer until it reaches the output after being processed in the hidden layer [84]. However, RBF basically differs from the MLP method as means of its hidden layers attitude where they adopt Gaussian function as follows:(4) $a_{j} (x) = \exp (\frac{x_{i} - c_{j}}{2 σ_{j}^{2}})$ where, c, x, and α denote the RBF center, input, and neuron width, respectively. While, j represents the neuron number. It can be further defined as follows:(5) $a_{j} (x) = \exp (- {(\frac{x}{σ})}^{2})$ (6) $a_{j} (x) = \exp (\frac{1}{{(σ^{2} + x^{2})}^{α}}), α > 0$ (7) $a_{j} (x) = {(α^{2} + x^{2})}^{β}, α < β < 1$ Then, the output ( $y_{k}$ ) is the sum of weighted RBFs unlike MLP method.(8) $y_{k} = \sum_{j = 1}^{J} w_{j k} R_{j} (x), k = 1, 2 \dots, K$ where, $w_{j k}$ gives the weights joining the nodes in the output and hidden layers. $K$ denotes the number of output layer neurons.

2.3. Random forests

The random forest (RF) method joins learning methods by employing several decision trees. Because there are so many trees, the decision is made according to the popular vote, which gains the necessity for computational source and power Fig. 8. Therefore, RF method features the ability to handle data with strong errors during learning and provides good accuracy even with poor learning dataset [85]. Besides, it is able to deal with nonlinear problems. However, this method is associated with complex training models due to hyperparameter confusion [86].

2.4. Support vector machine

The state-of-the-art support vector machine (SVM) method provides good practicality with fewer parameters and more simplicity in addition to high accuracy performance [88]. The train dataset is used for approaching relations among the dependent and independent variables, seeking to minimize the deviation between the predicted and the target data, as given in the layout in Fig. 9. SVM analyses the training values via creating a discriminant hyperplane, which further expects the memberships accurately by means of the new higher-dimensional space [89]. Appropriate penalty parameters are adopted, then the kernel function is employed to deal with linearly non-separable values to map the input data to the higher-dimensional feature space. Accordingly, the SVM is suitable for a few samples and high-dimensional nonlinear data predictions [83]. Finally, for all models, several statistical standards are often employed to evaluate their prediction accuracy, as in Table 1 [79].

Table 1

Factor	Formula	Indicator (Best value)
Mean square error	$M S E = \frac{1}{n_{S}} \sum_{i = 1}^{n_{S}} {(d_{i} - y_{i})}^{2}$	Zero
Mean relative error	$M R E = \frac{1}{n_{s}} \sum_{i = 1}^{n_{s}} \frac{d_{i} - y_{i}}{d_{i}}$	Zero
Mean absolute error	$M A E = \frac{1}{n_{S}} \sum_{i = 1}^{n_{S}} \| d_{i} - y_{i} \|$	Zero
Root mean square error	$R M S E = \sqrt{\frac{1}{n_{S}} \sum_{i = 1}^{n_{S}} {(d_{i} - y_{i})}^{2}}$	Zero
Coefficient of variance	$Cov = \frac{R M S E}{\frac{1}{n_{S}} \sum_{i = 1}^{n_{S}} y_{i}} \times 100$	Zero
Correlation coefficient	$Corr = \frac{n_{S} \sum_{i = 1}^{n_{S}} d_{i} y_{i} - (\sum_{i = 1}^{n_{S}} d_{i}) (\sum_{i = 1}^{n_{S}} y_{i})}{[n_{S} \sum_{i = 1}^{n_{S}} d_{i}^{2} - {(\sum_{i = 1}^{n_{S}} d_{i})}^{2}] [n_{S} \sum_{i = 1}^{n_{S}} y_{i}^{2} - {(\sum_{i = 1}^{n_{S}} y_{i})}^{2}]}$	1
Coefficient of determination	$R^{2} = \frac{{(\sum_{i = 1}^{n_{S}} (d_{i} - \overline{d}) (y_{i} - \overline{y}))}^{2}}{\sum_{i = 1}^{n_{S}} {(d_{i} - \overline{d})}^{2} \times \sum_{i = 1}^{n_{S}} {(y_{i} - \overline{y})}^{2}}$	1
Efficiency coefficient	$E C = 1 - \frac{\sum_{i = 1}^{n_{S}} {(d_{i} - y_{i})}^{2}}{\sum_{i = 1}^{n_{S}} {(d_{i} - \overline{d})}^{2}}$	1
Overall index of model performance	$O I = \frac{1}{2} (1 - (\frac{R M S E}{d_{\max} - d_{\min}}) + E C)$	1
Coefficient of residual mass	$C R M = \frac{\sum_{i = 1}^{n_{S}} y_{i} - \sum_{i = 1}^{n_{S}} d_{i}}{\sum_{i = 1}^{n_{S}} d_{i}}$	Zero

y and d denote the predicted and experimental value, respectively. $\overline{d}$ and $\overline{y}$ denote the average experimental and average predicted value, respectively. $d_{\max}$ and $d_{\min}$ are the maximum and minimum experimental values, respectively.

2.5. Solar still performance descriptors

2.5.1. Energy efficiency

It is an indicator that refers to the energy utilization efficiency of the system, which is the ratio between the system's output to input energy. For the SS case, the input is the solar energy and the rated power of active devices, if it exists. The output energy is represented by the required energy to evaporate the distillate water [90,91]. The following formulas are used for obtaining the hourly ( $η_{h r})$ or daily ( $η_{d}$ ) energy efficiency of SS:(9) $η_{h r} = \frac{{\dot{m}}_{w} \times h_{l}}{((I (t) \times A_{g}) + (W_{d})) \times 3600}$ (10) $η_{d} = \frac{\sum ({\dot{m}}_{w} \times h_{l})}{\sum [((I (t) \times A_{g})) \times 3600] + (W_{d}) \times τ}$ (11) $h_{l} = 2.5019 \times 10^{6} - 2.40706 \times 10^{3} \times T_{w} + 1.192217 \times {T_{w}}^{2} ‐ 158.63 \times 10^{‐ 4} \times T_{w}^{3}$ where, ${\dot{m}}_{w}$ denotes the hourly distillate productivity. $h_{l}$ and $A_{g}$ stand for the latent heat (kJ/kg) and glass area (m²), respectively. $I (t)$ and $W_{d}$ represent the solar intensity (W/m²) and active devices rated power (W), respectively. $τ$ is the active devices' operating duration along the day (hr). T_w denotes the water temperature in the SS (°C).

2.5.2. Exergy efficiency

The term exergy defines the quality of energy, or in other meaning, the maximum possible work to be gained from an energy source. Therefore, the exergy efficiency defines the ratio of the output to the input quality of energy. It also represents a key factor that indicates the sustainability index of the system [31,92]. The following formulas are used for obtaining the hourly ( $η_{h r - E x})$ or daily ( $η_{d - E x}$ ) exergy efficiency of SS:(12) $η_{h r - E x} = \frac{E x e r g y o u t p u t ({E X}_{o u t} (t))}{E x e r g y i n p u t ({E X}_{i n} (t))}$ (13) $η_{d - E x} = \frac{\sum E x e r g y o u t p u t ({E X}_{o u t} (t))}{\sum E x e r g y i n p u t ({E X}_{i n} (t))}$ (14) ${E X}_{o u t} (t) = \frac{{\dot{m}}_{w} \times h_{l}}{3600} \times (1 - \frac{T_{a}}{T_{w} + 273})$ (15) ${E X}_{i n} (t) = (I (t) \times A_{g}) \times [1 - \frac{4}{3} \times (\frac{T_{a}}{T_{s}}) + \frac{1}{3} \times {(\frac{T_{a}}{T_{s}})}^{4}] + (W_{d})$ where, T_a and T_s are the ambient and sun temperatures (K), respectively.

3. Applications of machine learning in solar stills

3.1. Single slope solar stills

Single slope SS is the oldest and simplest design. It is favorable when it comes to applying new modifications or testing new models owing to their simplicity and low price. Therefore, the majority of machine learning models for SS prediction were tested on single slope SS.

Nazari et al. [93] suggested coupling the Imperialist Competition Algorithm with the Artiﬁcial Neural Network (ICA-ANN). The model was basically employed to predict the productivity, energy, and exergy efficiency of a single slope SS via six inputs, namely, ambient, water, basin, glass temperature, solar radiation, and time. The model, however, did not include the effect of the wind speed or any modifications, as the study only focused on evaluating the role of ICA. The ICA-ANN performance was compared to the basic ANN in terms of R² and MAE. For the three outputs, energy, exergy efficiency, and productivity, ICA-ANN exhibited an MAE reduction of 40.11, 53.35, and 54.3 % compared to the basic ANN, respectively. Furthermore, R² reached 0.9928, 0.9689, and 0.9924 showing increments of 0.0186, 0.045, and 0.028 compared to the basic ANN, respectively. In the same context, Chauhan et al. [94] tested six algorithms all coupled to ANN, namely, resilient backpropagation, one step secant, conjugate gradient Powell-Beale restarts, conjugate gradient Fletcher reeves update, Levenberg Marquardt (LM), and scaled conjugate gradient. They adopted the ANN model, where the input layer consisted of water and glass temperature, which were selected to obtain the thermophysical properties of the air inside the SS. Thermophysical properties, as the output layer, included density, enthalpy of vaporization, specific heat, thermal conductivity, dynamic viscosity, and partial pressures (at glass and water surfaces). Among these algorithms, the LM algorithm showed the lowest RMSE for each output, where it did not exceed 0.0039, whereas the highest RMSE was obtained by the conjugate gradient Powell-Beale restarts algorithm, where it reached 0.0445. Furthermore, the efficiency coefficient obtained for the LM algorithm reached a maximum value of 1. It did not fall than 0.9941 for partial pressure at the glass surface and dynamic viscosity, respectively, and its overall R² was about 0.99994.

Murugan et al. [95] employed machine learning models for selecting suitable climate conditions to maximize the outcomes of a single slope SS. Multilayer perceptron, support vector machines, random forest, decision trees, and linear regression models were the range of study. The study selected decision trees as the most accurate model which exhibited an MAE of 5.43. Furthermore, the model was applied to evaluate the dependence of water productivity on the water, cover, basin temperature, wind speed, and solar radiation. The results showed that the most critical parameters are basin, water, and glass temperature, all had almost the same influence on water productivity. Solar radiation exhibited a moderate effect on water productivity, and its influence on the glass temperature was higher than its influence on water and basin temperature. Finally, the wind speed showed almost zero effect on water productivity, which is not commonly known among the solar still scientists’ community.

The role of machine learning extends to evaluating SS performance with some sort of passive modifications, including thermal storage, nanofluids, corrugated basins, …etc. Two modified single slope SSs were studied by Chauhan et al. [96] experimentally and by employing multilayer ANN with the LM algorithm. They designed three SSs: basic SS, SS with Sandbags, and SS with permanent magnets. The study, however, did not include any findings associated with the distillers’ outcomes while they paid more attention to evaluating the ANN model. Considering these, the input layer contained water, cover, ambient (sandbags or magnet) temperature, and solar radiation, while the output layer was only water productivity. The efficiency coefficient was at its maximum for the SS with magnets while its minimum value was for the basic SS with values of 0.9903 and 0.9591, respectively. Furthermore, the model had RMSE between 0.0299 and 0.0546 for the same distillers, respectively. These findings may be below that obtained by Chauhan et al. [2], who used the same algorithm and ANN model. However, the latter was employed for an easier task, which was thermophysical properties' determination, which are all can be obtained by several well-known formulas.

Ghandourah et al. [97], via a study for enhancing the heat transfer characterization of SSs, used multilayer ANN with various algorithms, including particle swarm optimizer, genetic algorithm, and golden jackal optimizer. The idea for enhancing the heat transfer was to use an absorber plate made of aluminum or polycarbonate in addition to leaving an air cavity between the basin and the base for better insulation. The SS with aluminum absorber outperformed the one polycarbonate absorber as they exhibited daily productivity of 3.8 and 3.4 L/m². Furthermore, SS with aluminum absorber achieved higher energy and exergy efficiencies with ratios of 15.1 and 49.6 %. Among all models, ANN with golden jackal optimizer resulted in the most accurate data where its RMSE did not exceed 0.01 for obtaining the water productivity from both SSs with an efficiency coefficient close to 1. However, the energy efficiency RMSE was above 4.36, which is relatively high compared to the model by Nazari et al. [93] who used ICA-ANN, and the energy efficiency RMSE was below 1.3673. Elsheikh et al. [98] studied a single slope SS with thermal localization, which was mounted above wick material, both suspended by low-density foam on top of the water surface Fig. 10. This modification was expected to reduce the heat loss and improve the evaporation rate as the thermal localization material absorbs all the solar energy and the heat is only focused on a thin film for vaporization. Furthermore, the distiller was modeled via three machine learning models, namely, adaptive neuro-fuzzy inference (ANFIS), SVM, and ANN. The thermal localization showed performance progress from a thermal and economic perspective, where the exergy and energy efficiencies were augmented by 46 and 34 %. Besides, the cost dropped to 0.015 $/L, which is within the acceptable range for passive SS. The water depth was further tested; however, it showed an almost slight effect as the evaporation process takes place only at the thin layer of thermal localization that receives all the solar radiation. The results showed a 5 % productivity increase after increasing the water depth from 5 mm to 25 mm, which may be due to the increased insulation thickness, which is water in this case. For machine learning models, SVM outperformed the other models as its RMSE was 0.098 and 0.099 for the modified and basic SS, respectively. Moreover, its efficiency coefficient was close to 1, with an R² of 0.999 for both SSs. The SVM model was compared to another model named relevance vector machine in a study by Zayed et al. [99] which was conducted to evaluate the performance of a passive stepped SS with corrugates. Stepped SS reduces the water depth which in turn minimizes the thermal inertia, then rapid evaporation. On top of this, the corrugated basin increases the metal area exposed to the sun and provides a larger contact area connecting the water and the basin Fig. 11. Accordingly, the water productivity was boosted by 255 %, according to the authors. Furthermore, the exergy and energy efficiences were increased by 379 and 239 %, respectively. Still, SVM outperforms relevance vector machine, especially when it is coupled with the Gaussian function. The RMSE dropped to 0.0002, and R² recorded 0.9999. These values were 0.0988 and 0.597 for ANN, while for the relevance vector machine, they were 0.021 and 0.516, which is still beyond that of the SVM model. The study, however, did not include any prediction models for the thermal performance characterization factors.

In most cases, passive SSs are associated with poor water production. Therefore, active SS have had more attention in recent years owing to their higher water production capacity and their higher reliability. Models have been established to predict the outcomes of active SS, especially those with solar collectors and external condensers. Sohani et al. [100] introduced an active SS which was supplemented with a flat-plate collector with a daily yield of 6.92 L/m². The collector was designed with a front and rear wheel that provides variable inclination angles in order to optimize the solar collection Fig. 12. For the performance prediction, three ANN models were employed to obtain the distillate productivity and temperature of the water. RBF, backpropagation, and feedforward were the scope of the study, and the latter exhibited the highest R²for obtaining the distillate productivity which reached 0.963111 and the MAE was 3.56. For the water temperature, the radial basis function was the most accurate model, and its R² reached 0.977057 at an MAE of 2.82.

The state-of-the-art deep neural network (DNN) took part in SS optimization, as introduced by Victor et al. [101]. They used a new approach named black widow particle swarm optimization which was employed for modeling active SSs with solar collectors in two configurations, spiral and straight tube collectors. The study lacked proper analysis afterward the spiral tube collector performance was almost the same as the straight tube collector. Besides, the model recorded RMSE 67.98,354 which is away from the majority of ANN algorithms. However, utilizing a deep Q neural network as an optimizer showed SS performance progress, as reported by Jafari et al. [102]. The optimizer was used to enhance the performance of an active SS, which used a flat solar collector and nanofluid. Accordingly, a productivity increase of 25 % was recorded, as well as 32 % thermal efficiency augmentation.

Recently, SS with ultrasonic foggers has been experimentally studied in the past few years and its first machine learning modeling was carried out by Abd Elaziz et al. [103]. SSs with foggers deal with more operation conditions, including the number of foggers, operation period, fogger power, …. etc. Hence, the authors suggested employing machine learning models for performance prediction rather than the costly experimental work. Considering these, the random vector functional link (RVFL) model was adopted for the performance optimization as it was coupled with three optimizers; namely; heap-based, sine cosine algorithm, and manta ray foraging. The model used only the ambient conditions (wind speed, solar intensity, ambient temperature) as the input data to predict the distillate productivity and water temperature. Water temperature prediction was carried out at a minimum RMSE of 6.660341 using a heap-based optimizer. However, this value increased to 43.32034 for productivity prediction using the same optimizer. RMSE is relatively higher than previous studies, but most of these studies use more than six inputs, which simplifies the prediction task.

The above active modifications seek to boost the evaporation process without considering the required condensation load. Apart from these, using external condensers was considered in several studies all aiming to enhance the condensation process. Essa et al. [104] introduced an experimental study on a passive SS with an external condensation coil. The passive SS was compared with a basic SS, and the modified one exhibited 53.21 % productivity progress. Furthermore, the study was supplemented with three machine learning models for distillate productivity prediction. They used the traditional ANN and SVM optimizer; besides, a new optimizer named Harris Hawks was considered. Harris Hawks model outperformed the other models for predicting the active SS, while for passive SS the three models’ predictions were roughly alike. A minimum RMSE of 35.06 was reached for basic SS prediction. However, it was above 70.53 for active SS prediction. On the other hand, maximum R² of 0.9703 and 0.9835 were obtained for active and basic SS, respectively, using the Harris Hawks model. An upgraded study was carried out by the same group [105]. They included nano additives for enhancing the water thermophysical properties, which in turn increased the productivity by 100 and 140 % for aluminum and copper oxide, respectively. Furthermore, an upgraded RVFL model, named Ensemble RVFL, was introduced, which seeks to reduce the correlations between RVFL networks. Both Ensemble RVFL and RVFL, exhibited highly accurate prediction ability as the RMSE was below 0.021. Besides, Ensemble RVFL slightly outperformed the standalone RVFL, where it could reduce the prediction RMSE of active SS with copper oxide to 0.008 while it was 0.014 for the standalone RVFL. For all models, R² ranged between 0.942 and 0.991; all the metrics were obtained for the distillate productivity prediction, whereas no data was provided for thermal analysis characterization. Bahiraei et al. [106] used multilayer ANN with ICA and genetic algorithm for modeling a similar SS which uses copper oxide and an external condenser formed by four thermoelectric nodules. Furthermore, eight parameters were contained in the input layer, on top of the six known parameters, they considered nano additive concentration and the vapor fan power. The ICA-ANN model showed better agreement with the experimental data compared to genetic algorithms, which provided R² of 0.9726. Besides, a 62.01 % RMSE reduction was obtained compared to basic multilayer ANN. However, the model used only 48 points, which resulted in an MAE above 30.57 and the model still lacks thermal analysis characterization modeling. Therefore, another study by Nazari et al. [107] was introduced for predicting the exergy and energy efficiencies of an active SS. SS was supplemented with a dish concentrator, nanofluids, and external condenser with thermoelectric modules Fig. 13. The models named Evolutionary Polynomial Regression showed RMSE of 0.827 and 0.1078 for energy and exergy prediction. Esfe et al. [108] employed a genetic algorithm and Taguchi function for operating parameters' optimization of an active SS that uses thermoelectric coolers (TECs) for the condensation process. The parameters in the study were cooling rate, SS length, SS front height, and TEC length. The results ranked the strength of parameters according to their impact on the output, which was from the highest to lowest according to the mentioned order. Accordingly, at a 60 W/m² cooling load of SS length of 40 cm, 6 cm front height, and TEC length of 14 cm, a productivity improvement of 55 % was obtained.

3.2. Double slope solar still

Double slope SSs have several advantages over single slope SSs, where double slope SSs provide larger condensation cover, which provides faster condensation throughout the day. Besides, they receive solar radiation from two directions, which reduces the shade on SS during the second part of the day. Hence, several experimental studies and improvements were conducted on double slope SS. On top of that, several machine learning models were introduced to substitute for the money and time-consuming experimental work. Maddah [109] compared several algorithms that were employed to forecast the distillate productivity of a double slope SS. The author suggested linking the variation between the water and glass cover temperature with productivity. Then, the prediction task became easier as the productivity had a roughly linear relationship with the water-glass temperate difference. Subsequently, an R² of almost 1 was reached, and the RMSE did not exceed 7.7 for distillate productivity prediction. Kandeal et al. [86] investigated a modified double slope SS with a productivity of 4.3 L/m². The distiller was supplemented with 1.5 wt% of carbon black nanofluid to improve the thermophysical properties of raw water. The authors employed four machine learning models, namely, ANN, support vector regression, linear support vector regression, and random forest for predicting the performance. The latter showed the best agreement with the experimental data as it recorded an R² of 0.997 and an error percentage of 2.95 %. Furthermore, the study explores the influence of each parameter on productivity. The water temperature showed a 66.63 % impact followed by the vapor temperature of 13.76 % impact. Unlike single slope SS, the glass temperature effect slightly declined as its impact ratio was 6.14 % as the large glass area substituted for the temperature impact. Since the study did not include a prediction for the system efficiency, Sharshir et al. [110] provide several models for predicting the productivity and the efficiency of a modified double slope SS, given in Fig. 14. The SS was modified with cotton-wicked flat steps in the two directions in addition to 1 wt% cobalt oxide implementation. The results showed an average daily yield of 4 L/m² at an efficiency of 38 %. For the modeling, they included four models; namely: ANN, decision tree regressor, SVR, and DNN. The latter exhibited the highest prediction accuracy for both productivity and efficiency. For the efficiency prediction, RMSE was 0.9 at R² of 0.9953. The RMSE increased to 3.3 for the productivity prediction, but with a better R² as it recorded 0.9998. Additionally, the study showed the impact of each parameter on productivity. The solar radiation showed 40.22 % impact followed by water temperature of 27.62 % impact. Solar radiation appeared as a major factor in this model, unlike the model by Kandeal et al. [86] because the current model deals with thermal efficiency which is directly governed by solar radiation. Still, the glass temperature has a low impact, unlike single slope SS.

Active double slope SSs were considered in a few studies as Bagheri et al. [111] modeled an active SS using the basic multilayer ANN, presented in Fig. 15. The SS was supplemented with a solar collector and PV unit for powering electric heaters, which could provide hot water all over the day. On the other hand, the input layer of the model used the temperature of ambient, glass, water, basin, and insulation in addition to the voltage and current of the heater. These parameters were inputted for predicting water productivity. Basically, it is a relatively easy task since these data are directly proportional to productivity, unlike the models that use only the weather conditions. As expected, the MSE was almost zero, with an R² of 0.999820171. Another active double slope SS was modeled by Salem et al. [112]. The system was closer to being a water heater HDH desalination unit, as in Fig. 16, as it uses the SS as a humidifying chamber with solar water heaters. Furthermore, the study included three models: multilayer ANN, Bayesian ridge regression, decision trees, and multilayer ANN with Adam optimization. The latter demonstrated the best data prediction with an RMSE of 0.07171.

3.3. Inclined solar still

Inclined SS is a single slope SS with a basin parallel to the glass cover. It has several advantages over the known single slope SS as the inclined basin receives the solar radiation vertically at midday. Besides, less shadow is cast on the water which is a major disadvantage that faces the conventional SS. On top of that, inclined SS provides a larger basin area at the same projected surface area of a single slope SS which in turn increases the distiller thermal efficiency. Herein, a review is associated with inclined SS modeling via machine learning modes.

Mashaly and Alazba [113] used multilayer ANN with three algorithms for modeling an inclined SS Fig. 17. The algorithms considered in the study were resilient backpropagation, conjugate gradient backpropagation with Fletcher–Reeves restarts, and LM algorithm for all models, brine, feed, ambient temperature, brine total dissolved solids (TDS), raw water TDS, wind speed, relative humidity, and solar radiation. The model testing showed that the ML algorithm has the most accurate productivity prediction. These results agree with the results obtained by Chauhan et al. [94] who compared these three in addition to three others. The minimum testing RMSE was recorded by the LM algorithm, which recorded an RMSE of 0.027. Furthermore, the efﬁciency coefﬁcient recorded 0.983 during the model testing. However, conjugate gradient backpropagation exhibited a higher efﬁciency coefﬁcient as it reached 0.985. Nevertheless, the LM algorithm outperformed the others during the validation phase, showing RMSE and efﬁciency coefﬁcient of 0.016 and 0.996, respectively. This study was followed by several studies in which the same authors modeled the same SS design using different machine learning models with different algorithms. Back-propagation ANN was compared with the stepwise regression model [114] with the same inputs as their previous study for predicting the distillate productivity. The ANN model provides a more accurate prediction, which exhibited RMSE of 0.047 L/m²/h and R² of 0.96. Following the study, the authors employed ANFIS for productivity prediction [115]. In this study, the inputs were reduced to five parameters where the water and brine temperature were replaced with the feed flow rate. Furthermore, several membership functions of fuzzy sets were considered in order to reach the most accurate results. Furthermore, the models selected solar radiation as the most impactful parameter, followed by feed flow rate. According to the highlighted results, ANFIS showed accurate results compared to ANN models in the previous study [114] as the RMSE dropped to 0.0041 L/m²/h in addition to correlation coefﬁcient of 0.9999. However, these findings were obtained during the training process while for the testing process, these values dropped to 0.0871 and 0.9367, which is still beyond that of ANN. This observation is confirmed in a study that compared multiple regression (MLR), ANFIS, and ANN performance in productivity forecasting of the same system with the same input parameters [116]. The ANN models outperformed the other models during the testing process as its RMSE and correlation coefﬁcient recorded 0.055 and 0.973 while these values were 0.07 and 0.959 for ANFIS, then 0.134 and 0.941 for MLR. Considering that ANFIS showed the lowest RMSE during the training process, where it showed a value of 0.001 while it was 0.028 and 0.125 for ANN and MLR, respectively.

Abujazar et al. [117] employed an ANN model named cascaded forward neural network for productivity forecasting of a modified inclined SS. They used an inclined SS with a stepped basin with a V-corrugated structure which would increase the metal area exposed to the sun and provide a larger water-basin contact area, then higher productivity. Furthermore, twelve parameters were selected as input data all employed seeking the most accurate productivity prediction Fig. 18. Accordingly, the model showed RMSE of 0.2248 likewise 0.04101 L/m²/h. These findings were below that obtained by mathematical and regression models which demonstrated RMSE of 0.4406 and 0.2735, respectively. In the same context, Pavithra et al. [118] combined Harris Hawk's Optimizes with the ANN model (HHO-ANN) for forecasting the yield of a wick-provided inclined SS Fig. 19. HHO-ANN model was compared to an ANN model where the latter exhibited higher RMSE. For HHO-ANN and ANN, the recorded RMSE was 38.131 and 39.84, respectively. Furthermore, the ANN model considered two models, namely, feed-forward and radial basis function, for thermal efficiency prediction which was obtained as 59.78 %. Overall, HHO-ANN showed moderate accuracy for hourly and monthly yield prediction, where their obtained error ranged between 8.13-6.1 % and 0.95–1.12 %, respectively.

A third modification by Sharshir et al. [119] was considered where they placed a copper absorber under the wick layer of a wick-inclined SS Fig. 20. Hence, the existence of the copper absorber could provide 50 % higher productivity compared to the wick-inclined SS with conventional basin. Furthermore, the tree–seed algorithm was combined with the ANN model to optimize the neurons' weights. The new model provided productivity prediction with RMSE of 0.086 and 0.0475 for the modified and non-modified SS, respectively. Instead, standalone ANN exhibited RMSE of 0.108 and 0.084 for the two SSs, respectively.

3.4. Pyramid solar still

Reaching pyramid SS, which, in some cases, is called four slope SS as its condensation cover is formed in a pyramid shape. The pyramid condensation cover provides a larger area for condensation compared to that of double or single-slope SSs, which in turn affords a more efficient condensation process. Besides, this structure allows solar receiving from any direction along the day providing higher thermal efficiency and minimum shade on the basin. Verma and Namdev [120] conducted a simple study that compares the performance of three SS designs: single slope, double slope, and pyramid SS. As expected, pyramid SS showed the highest productivity followed by double slope SS, whereas the single SS had the lowest distillate productivity. Furthermore, they tested three models for productivity predicting, linear regression, ANN, and improved ANN. The latter had the most accurate prediction with an accuracy of 87–94 % which was higher than the basic ANN of a prediction accuracy of 67–79 %. The lowest prediction accuracy was caused by linear regression, which had values between 64 and 74 %. The study was only associated with a simple comparison between the models without including other models’ assessment factors.

Peng et al. [121] performed a study that surveyed the impact of the dataset size on the prediction accuracy of three machine learning models, namely ANN, RF, and MLR. The dataset was collected from a lab-based SS which simulates the real environmental conditions Fig. 21. A fan was mounted for controlling the vapor rise to the condensation cover. The input dataset included the temperature of ambient, water, and glass. For the fan, the input data considered the fan's power and its height. Furthermore, a sixth input factor considered the SS type as the study involved single slope, double slope, and pyramid SS in order to generalize the findings. According to the study, ANN is highly affected by the dataset size in the range of 100–400 then the dataset size influence declines. Conversely, the random forests model is affected by the dataset size for the entire range of study (100–1000), while MLR was not affected by the dataset size. The forecasting accuracy of the ANN model outperformed the other models at any data set size, where 93.4 % of its predicted results were below an error of 10 %. On the other hand, MLR showed higher accuracy compared to random forests in the range of 100–300 dataset size; then random forest models showed accuracy until it was close to the ANN model at dataset size of 1000.

Elgendi and Atef [122] performed a study that examined the number of inputs effect on productivity prediction accuracy. The complete input set consisted of the temperature of ambient, glass, vapor, feed, and water. Besides, several weather parameters are considered as follows: solar intensity, wind speed, ultraviolet index, relative humidity, THW index (temperature-humidity-wind effect), and THSW index (temperature-humidity-solar-wind effect). The ANN model showed an RMSE of 8.12 when the input layer included only solar radiation and feed temperature then decreased to 7.06 after including the ambient temperature. Since the SS design was pyramid SS, the wind speed had a major impact on the results, as previously explained in double slope SS. Accordingly, the RMSE declined to 6.77 by including the wind speed in the input layer. Finally, the RMSE dropped to 4.97 when the entire dataset was used as the input layer. Linear regression was also considered throughout the study. However, its RMSE ranged between 12.87 and 9.99. Alsaiari et al. [123] introduced a new algorithm named rabbits optimizer, which was coupled with multilayer ANN. They also consider several models for comparing the new model, namely, basic multilayer ANN, ANN with genetic algorithm, and ANN with particle swarm, for a pyramid SS, an RMSE of 84.141, 46.281, 37.688, and 4.385 for ANN, ANN with genetic algorithm, ANN with particle swarm, and ANN with rabbits optimizer, respectively.

3.5. Tubular solar still

Tubular SS is a design that gets rid of the large basin and uses a smaller trough hung in the middle of a transparent tube. This design provides the best solar tracking among SS designs, as it can receive solar rays from any direction. Besides, the tube surface area is much larger than the trough area, which in turn allows better condensation. It is worth mentioning that tubular SS construction somehow limits the application of different modifications. Therefore, most of machine learning studies associated with tubular SS only shared new models for productivity and thermal efficiency prediction of basic tubular SS.

In the previously mentioned study, Alsaiari et al. [123] considered several SS designs. Among these designs, tubular SS modeling was associated with the lowest RMSE since it dropped to 0.894 using ANN with the rabbit's optimizer model. Wang et al. [124] used several models for predicting the distillate productivity of a basic tubular SS. The study aimed to evaluate the role of combining Bayesian optimization with ANN and random forest models. Furthermore, the MLR model was employed as a reference for comparing the prediction accuracy progress of the new models. For all models, the input parameters were ambient conditions (time, wind speed, ambient temperature, and solar intensity) and SS conditions (water, basin, feed, and glass temperature). Random forest with Bayesian optimization model showed the most precise prediction compared with other models where the obtained MAE% was 10.911, 7.697, and 5.21 % for MLR, Bayesian optimization-based ANN, and Bayesian optimization-based random forest model. On another scale, the obtained R² was 0.9267, 0.9614, and 0.9758 for the three models, respectively. Similarly, Saravanan et al. [125] introduced three different models for productivity prediction of tubular SS with different wick materials. The models in the study were K-nearest neighbors, linear regression, and decision tree. The models were set to obtain the productivity and the thermal efficiency of the distiller with input data, including weather conditions (wind speed, ambient temperature, and solar intensity) and SS parameters (water and glass temperature). The most accurate prediction was observed using the decision tree model, which exhibited prediction accuracy of 96 % at RMSE and R² of 0.85135 and 0.9602, respectively. However, these values were changed to 94 %, 0.959068, and 0.619375 for linear regression, then to 75 %, 1.610476, and 0.849896, respectively.

Moustafa et al. [126] introduced an active tubular SS that uses an electric heater operated via a PV panel Fig. 22. The experimental work showed a yield improvement of 31.85 % compared to the passive tubular SS as the productivity increased from 2.58 L/m² to 3.41 L/m². Besides, the thermal efficiency increased from 30.67 % to 38.61 %. The study further included three models for the forecasting of yield and efficiency. A new optimizer named humpback whale was coupled with the conventional ANN model and compared with conventional ANN and ANN with particle swarm optimizer. The new optimizer combined with the ANN model exhibited the most accurate productivity and efficiency prediction for the active and passive SS. An efficiency coefficient of 0.992 and 0.999 were obtained for the active SS productivity and efficiency prediction, respectively.

3.6. Hemispheric solar still

Hemispheric SS is an intermediate design that combines the advantages of both basin and tubular SSs. It provides moderate solar tracking, and its condensation cover is large enough for the condensation process. In addition, it is easily fabricated and installed, unlike tubular SSs. Since hemispheric SS is considered a recent design, few studies have been conducted for modeling its performance using the machine learning method.

Bamasag et al. [127] conducted an experimental study supplemented with machine learning models for productivity prediction. They applied several modifications seeking better energy utilization, which in turn increased the distillate productivity. Firstly, they constructed a stepped dome with wick material inside the distiller. Then, the cavity below the dome was filled with nano-based phase change material (PCM), as in Fig. 23. At the optimum water depth, 1.5 cm, the distiller exhibited productivity of 6.525 L/m² without including the PCM, which further increased the productivity to 8.2 L/m² showing productivity augmentation of 178 %. Moreover, the obtained thermal efficiency reached 67.62 %, while it did not exceed 31.71 % for the basic design. For the machine learning modeling, they employed ANN, ANFIS, and SVM for productivity prediction. SVM was way more accurate compared to ANN and ANFIS modes, where it predicted the productivity of the modified SS with RMES and R² of 2.193044 and 0.999959. On the other hand, these values deflected to 222.2553 and 0.716384 for the ANFIS model, then 227.6265 and 0.906968 for the ANN model. In the same context, an alike study was done by Ashraf et al. [128] as they compared the performance of basic multilayer ANN, multilayer ANN with an improved genetic algorithm, and ANN with particle swarm optimization. Furthermore, the study considered the effect of fin profile on the distillate productivity as they tested hemispheric SS with different fin profiles and different spacing. The model with an improved genetic algorithm was superior to the other models as for all the results, its RMSE laid between 0.163 and 0.011, while this range increased to 0.802–0.097 for the particle swarm optimization model and 2.145–0.705 for the standalone model.

Table 2 provides a summary of the findings reached by different models for each SS type as appeared in the literature. It can be noticed that the prediction of SSs’ performance can be successfully and accurately conducted by ML models. According to the table, different robust models have been discovered for the variety of SS types.

Table 2

SS type	Model	RMSE	R²	Reference
Single slope	ANN with Levenberg Marquardt algorithm	0.0039	0.99994	Chauhan et al. [94]
Single slope	ANN with Levenberg Marquardt algorithm	0.0299–0.0546	–	Chauhan et al. [96]
Single slope	ANN with Golden Jackal Optimizer	0.01	–	Ghandourah et al. [97]
Single slope	Support vector machine	0.098–0.099	0.999	Elsheikh et al. [98]
Single slope	Support vector machine	0.0002	0.9999	Zayed et al. [99]
Single slope	Radial basis function	MAE = 2.82	0.977057	Sohani et al. [100]
Single slope	Random vector functional link	43.32034	–	Abd Elaziz et al. [103]
Single slope	Deep neural network	67.98354	–	Victor et al. [101]
Single slope	Harris Hawks optimizer	70.53	0.9703	Essa et al. [104]
Single slope	Ensemble random vector functional link	0.008	0.991	Essa et al. [105]
Single slope	ANN with Imperialist Competition Algorithm	MAE = 30.57	0.9726	Bahiraei et al. [106]
Double slope	Random forest	Percentage error = 2.95 %	0.997	Kandeal et al. [86]
Double slope	Deep neural network	3.3	0.9998	Sharshir et al. [110]
Double slope	ANN	MSE ≈ 0	0.999820171	Bagheri et al. [111]
Double slope	ANN with Adam optimization	0.07171	–	Salem et al. [112]
Inclined	ANN with Levenberg Marquardt algorithm	0.027	–	Mashaly and Alazba [113]
Inclined	Back-propagation ANN	0.047	0.96	Mashaly and Alazba [114]
Inclined	Adaptive neuro-fuzzy inference	0.0871	0.9367	Mashaly and Alazba [115]
Inclined	Cascaded forward neural network	0.2248	–	Abujazar et al. [117]
Inclined	ANN with tree–seed algorithm	0.0475–0.086	–	Sharshir et al. [119]
Pyramid	ANN	4.97	–	Elgendi and Atef [122]
Pyramid	ANN with rabbits optimizer	4.385	–	Alsaiari et al. [123]
Tubular	ANN with rabbits optimizer	0.894	–	Alsaiari et al. [123]
Tubular	Bayesian optimization-based random forest	MAE% = 5.21 %	0.9758	Wang et al. [124]
Tubular	Decision tree	0.85135	0.9602	Saravanan et al. [125]
Hemispheric	Support vector machine	2.193044	0.999959	Bamasag et al. [127]
Hemispheric	ANN with an improved genetic algorithm	0.011–0.163	–	Ashraf et al. [128]

4. Conclusions

This work aimed to present a comprehensive overview of the applicability and viability of machine learning-based prediction of solar stills' performance. Accordingly, the research trend was analyzed to give insightful identification of the research area, international collaboration, and trends over time. Then, the mostly considered machine learning methods that have been applied to solar stills' performance prediction were discussed in terms of principle, advantages, limitations, and mathematical description. The statistical descriptors of the models’ accuracy were also given. Besides, the thermal performance of solar stills was also focused, and the distillers were classified according to the design to give more concise discussions and analyses. Moreover, the contributions and limitations of each model were being surveyed throughout the work. The following point highlights the major notices:

•
The applicability of machine learning in the prediction of solar stills' performance has been updated till it has become a main part of several studies.
•
Multiple regression models can exhibit moderate prediction accuracy regardless of the dataset size. In contrast, ANN models are affected by the dataset size in the range of 100–400, with accuracy higher than multiple regression models.
•
The prediction accuracy differed from one model to another. For example, Support vector machine, ANN, Back-propagation ANN, and Bayesian optimization-based random forest showed robust prediction performance for single-slope and hemispheric, double-slope, inclined, and tubular SSs, respectively.
•
Few models were applied for thermal efficiency prediction, the most accurate prediction was reached using ANN coupled with the Imperialist Competition Algorithm and achieved RMSE of 1.3673 at six input neurons.
•
Adaptive neuro-fuzzy inference models are often associated with low RMSE during the learning process, while ANN and support vector machine models show lower RMSE during testing.

CRediT authorship contribution statement

A.S. Abdullah: Writing – review & editing, Validation, Data curation, Conceptualization. Abanob Joseph: Resources, Writing – original draft, Formatting, Analysis. A.W. Kandeal: Writing – original draft, Visualization, Revision. Wissam H. Alawee: Writing – review & editing, Data curation, Conceptualization. Guilong Peng: Resources, Writing – review & editing. Amrit Kumar Thakur: Resources, Writing – original draft, Formatting, Analysis. Swellam W. Sharshir: Writing – original draft, Visualization, Validation, Supervision, Software, Resources.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgment

The authors extend their appreciation to Prince Sattam bin Abdulaziz Universityfor funding this research work through the project number (2023/RV/01)"

Data availability

No data was used for the research described in the article.