Heat and mass transfer characteristics of nanofluid over horizontal circular cylinder

1. Introduction

Natural convection flow, heat and mass transfer through porous medium over curved bodies is an important area in the recent years because of its wide range applications such as chemical engineering, thermal energy storage devices, heat exchangers, ground water systems, electronic cooling, boilers, heat loss from piping, nuclear process systems. Spherical geometries, cones, cylinders, ellipses, wavy channels, and torus geometries are some examples of curved bodies. Good number of experimental and theoretical studies on transport phenomena over cylindrical bodies has been reported in the literature which deals with the process of polymer systems. All these studies are mainly focused on flow and heat transfer characteristics of the commonly used base fluids such as water, ethylene glycol, oil.

A nanofluid is a fluid containing small volumetric quantities of nanometer-sized (smaller than 100 nm) particles called nanoparticles. Nanofluids are the emerging composites consisting of nanometer size solid particles dispersed in the conventional heat transfer fluids such as water, ethylene glycol, toluene, and engine oil. The nanoparticles used in nanofluids are typically made of metals (Al, Cu), oxides (Al2O3, CuO, TiO2, SiO2), carbides (SiC), nitrides (AlN, SiN), or nonmetals (graphite, carbon nanotubes). In the recent years, the concept of a nanofluid has been proposed as route for enhancing the performance of the heat transfer rates in liquids. The materials that are in nanometer size possess unique physical and chemical properties. They can flow smoothly through micro-channels without clogging because they are sufficiently small to behave similar to liquid molecules. This fact has attracted much research into the investigation of the heat transfer characteristics in nanofluids. Many experimental and numerical studies reported that the presence of nanoparticles increases the thermal conductivity of the base fluid in the range of 15–40%. Increases in the thermal conductivity of this magnitude cannot be solely attributed to the higher thermal conductivity of the added nanoparticles. There must be other mechanisms, which include particle agglomeration, nanoparticle size, volume fraction, Brownian motion, thermophoresis, particle shape, surface area, temperature and liquid layering on the nanoparticle–liquid interface, attributed to the increase in performance of the nanofluids. Conventional heat transfer fluids such as water, ethylene glycol, and engine oil have limited heat transfer capabilities due to their low heat transfer properties. In contrast, metals have thermal conductivities up to three times higher than these fluids, so it is naturally desirable to combine the two substances to produce a heat transfer medium that behaves like a fluid, but has the thermal properties of a metal. Choi [1] was the first among all who introduced a new type of fluid called nanofluid while doing research on new coolants and cooling technologies. Eastman et al. [2] have noticed in an experiment that the thermal conductivity of the base fluid (water) has increased up to 60% when CuO nanoparticles of volume fraction 5% are added to the base fluid. This is because of increasing surface area of the base fluid duo to the suspension of nanoparticles. Eastman et al. [3] have also showed that the thermal conductivity has increased 40% when copper nanoparticles of volume fraction less than 1% are added to the ethylene glycol or oil. Choi et al. [4] have reported that there is 150% enhancement in thermal conductivity when carbon nanotubes are added to the ethylene glycol or oil. In addition, Xie et al. [5] have observed that Al2O3–ethylene glycol based nanofluid thermal conductivity is increased in the range 25–30% when Alumina nanoparticles are added. Buongiorno [6] has reported seven possible mechanisms associating convection of nanofluids through moment of nanoparticles in the base fluid using scale analysis. These are nanoparticle size, inertia, particle agglomeration, Magnus effect, volume fraction of the nanoparticle, Brownian motion, thermophoresis. Among all the mechanisms Brownian motion and thermophoresis are found to be very important. The thermophoresis acts against temperature gradient, so that the particles move from the region of higher temperature to the region of lower temperature. Also, Brownian motion tends to move the particles from higher concentration areas to lower concentration areas. Nield and Kuznetsov [7] have discussed the Cheng–Mincowycz problem for natural convection boundary-layer flow in a porous medium saturated nanofluid. Kuznetsov and Nield [8] studied the influence of Brownian motion and thermophoresis on natural convection boundary layer flow of a nanofluid past a vertical plate. Khan and pop [9] have discussed boundary layer flow of a nanofluid past a stretching sheet. Chamkha et al. [10] studied the mixed convection MHD flow of a nanofluid past a stretching permeable surface in the presence of Brownian motion and thermophoresis effects. Noghrehabadi et al. [11] have presented heat and mass transfer characteristics of non-Darcy natural convection flow of a nanofluid over a vertical cone through porous media. Furthermore, Noghrehabadi and Behseresht [12] have analyzed the flow and heat transfer characteristics of nanofluid over a vertical cone saturated in a porous medium. Chamkha et al. [13], [14] have discussed the mixed, natural convection flow about vertical cone and vertical cylinder through porous medium saturated by a nanofluid respectively. Rashad et al. [15] presented mixed convective boundary layer flow of a nanofluid about horizontal cylinder embedded in a porous medium under convective boundary conditions. Nasrin et al. [16], Chamkha et al. [17], Parvin et al. [18], Abu-nada and Chamkha [19] have reported flow and heat transfer characteristics of nanofluid over different geometries such as, double lid-driven chamber, partially heated porous layered cavities, odd-shaped cavity, lid-driven cavity in wavy wall, respectively. Kuznetstov and Neild [20] have presented a revised model of natural convection boundary layer flow of a nanofluid past a vertical plate. In this paper the existing model is revised so that the nanofluid particle fraction on the boundary is passively controlled rather than actively controlled and this model is physically more realistic than the works published previously. Sheikholeslami et al. [21] have analyzed natural convection flow of nanofluid over a horizontal circular cylinder with the influence of magnetic field. Sheikholeslami and Ganji [22] have presented Ferrohydrodynamic and Magnetohydrodymic effects on ferrofluids. Sheikholeslami [23] has discussed flow and heat transfer analysis of nanofluid over a permeable channel under the KKL correlation for simulation. Ravi kumar et al. [24] have reported MHD convective Rivlin-Ericksen flow over a vertical plate by taking variable temperature and heat absorption. Rashidi et al. [25] have studied the MHD free convection heat and mass transfer flow over a vertical stretching sheet in the presence of thermal radiation and buoyancy effects. Good number of representative studies over heat and mass transfer characteristics of different nanofluids over different geometries can be found in [26], [27], [28], [29], [30], [31], [32], [33], [34], [35], [36]. Seyyedi et al. [37] have reported natural convection heat transfer over annulus filled with nanofluid under the influence of constant heat flux. Srinivasacharya et al. [38] have studied mixed convective heat and mass transfer flow over a vertical wavy surface through porous medium with Soret and Dufour effects. Sudarsana Reddy and Suryanarayana Rao [39] have investigated MHD natural convection heat and mass transfer of Al2O3–water and Ag–water nanofluids over a vertical cone with chemical reaction.

An inspection of the existing literature suggests that, to the best of author’s knowledge, no studies have been reported to study natural convection boundary layer flow, heat and mass transfer characteristics of a nanofluid over a horizontal circular cylinder placed in a porous medium under the revised boundary conditions [20]. Hence, the problem is addressed here and the objective of the present work was to solve this problem numerically using the Finite element method. The problem addressed here has applications in micro-electromechanical systems, nuclear reactors, electronic cooling equipment, transportation, heating and cooling process of energy conversion. At present, the analysis of nanofluids is a topic of great interest to modern researchers due to its importance in industry and medicine. In addition, the magneto nanofluids have great importance in the construction of power generators, petroleum reservoirs, cancer therapy, wound treatment, gastric medications, and elimination of tumors with hyperthermia, asthma treatment, and sterilized devices.

2. Formulation of the problem

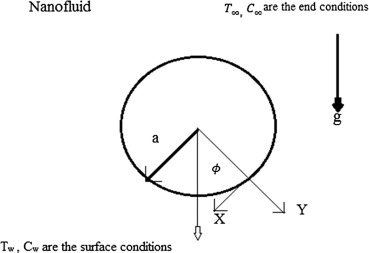
Fig. 1 illustrates a two-dimensional study, laminar, incompressible, natural convection boundary layer flow about a horizontal circular cylinder of radius ‘a’ placed in a porous medium saturated with nanofluid. The coordinate system is chosen as the x-coordinate (tangential) measured along the circumference of the horizontal cylinder from the lowest point and y-coordinate (radial) is measured perpendicular to the surface. The model used for the nanofluid incorporates the effects of Brownian motion and thermophoresis. The horizontal cylinder and nanofluid are maintained at uniform temperature Tw, the concentration of nanoparticles at the surface of the cylinder is controlled by the condition DB(∂C/∂y) + (DT/T∞)(∂T/∂y) = 0 and these values are assumed to be greater than the ambient temperature and concentration, $T_{\infty}$ and $C_{\infty}$ , respectively. $γ = \frac{x}{a}$ is the angle of the y-axis with respect to the vertical $0 ⩽ γ ⩽ π$ . By employing the Oberbeck–Boussinesq approximation and by following Kuznetsov and Neild [20] revised model, the governing equations describing the steady-state conservation of mass, momentum, energy as well as conservation of nanoparticles for nanofluids take the following form:(1) $\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0$ (2) $\frac{\partial p}{\partial y} = 0$ (3) $μ_{nf} \frac{1}{κ} u = - \frac{\partial p}{\partial x} + g [(1 - C_{\infty}) ρ_{f \infty} β (T - T_{\infty}) - (ρ_{p} - ρ_{f \infty}) (C - C_{\infty})] Sin (\frac{x}{a})$ (4) $(u \frac{\partial T}{\partial x} + v \frac{\partial T}{\partial y}) = \frac{k_{nf}}{{(ρ c_{p})}_{nf}} \frac{\partial^{2} T}{\partial y^{2}} + \frac{{(ρ c_{p})}_{f}}{{(ρ c_{p})}_{nf}} [D_{B} \frac{\partial C}{\partial y} . \frac{\partial T}{\partial y} + (\frac{D_{T}}{T_{\infty}}) {(\frac{\partial T}{\partial y})}^{2}]$ (5) $\frac{1}{ε} (u \frac{\partial C}{\partial x} + v \frac{\partial C}{\partial y}) = D_{B} \frac{\partial^{2} C}{\partial y^{2}} + (\frac{D_{T}}{T_{\infty}}) \frac{\partial^{2} T}{\partial y^{2}}$

The boundary conditions based on the problem description are as follows:(6) $u = 0, v = 0, T = T_{w}, D_{B} \frac{\partial C}{\partial y} + (\frac{D_{T}}{T_{\infty}}) \frac{\partial T}{\partial y} = 0 at y = 0$ (7) $u \to 0, T \to T_{\infty}, C \to C_{\infty} at y \to \infty$

The stream function ψ is defined as follows:(8) $u = \frac{\partial ψ}{\partial y}, v = - \frac{\partial ψ}{\partial x}$

By cross-differentiation p may be eliminated and using the aforesaid stream function the Eqs. (2), (3), (4), (5) can take the following form:(9) $\frac{\partial^{2} ψ}{\partial y^{2}} = [\frac{(1 - C_{\infty}) ρ_{f \infty} β gk}{μ_{nf}} \frac{\partial T}{\partial y} - \frac{(ρ_{p} - ρ_{f \infty}) gk}{μ_{nf}} \frac{\partial C}{\partial y}] Sin (\frac{x}{a})$ (10) $\frac{\partial ψ}{\partial y} \frac{\partial T}{\partial x} - \frac{\partial ψ}{\partial x} \frac{\partial T}{\partial y} = \frac{k_{nf}}{{(ρ c_{p})}_{nf}} \frac{\partial^{2} T}{\partial y^{2}} + \frac{ε {(ρ c_{p})}_{f}}{{(ρ c_{p})}_{nf}} [D_{B} \frac{\partial C}{\partial y} \frac{\partial T}{\partial y} + (\frac{D_{T}}{T_{\infty}}) {(\frac{\partial T}{\partial y})}^{2}]$ (11) $\frac{1}{ε} (\frac{\partial ψ}{\partial y} \frac{\partial C}{\partial x} - \frac{\partial ψ}{\partial x} . \frac{\partial C}{\partial y}) = D_{B} \frac{\partial^{2} C}{\partial y^{2}} + (\frac{D_{T}}{T_{\infty}}) \frac{\partial^{2} T}{\partial y^{2}}$

The following similarity transformations are introduced to simplify the mathematical analysis of the problem:(12) $η = \frac{y}{x} {Pe}_{x}^{1 / 2}, f (η) = \frac{ψ}{α_{m} {Pe}_{x}^{1 / 2}}, θ (η) = \frac{T - T_{\infty}}{T_{w} - T_{\infty}}, ϕ (η) = \frac{C - C_{\infty}}{C_{w} - C_{\infty}}$ where $α_{m} = \frac{k_{nf}}{{(ρ c_{p})}_{nf}}$ .

Using the similarity variables, Eqs. (9), (10), (11) are reduced into the following three ordinary differential equations:(13) $f^{″} - Ra (θ^{'} - Nr ϕ^{'}) Sin (ξ) = 0$ (14) $θ^{″} + \frac{1}{2} ξ Cot (ξ) f θ^{'} + Nb θ^{'} ϕ^{'} + Nt {(θ^{'})}^{2} = 0$ (15) $ϕ^{″} + \frac{1}{2} Le ξ Cot (ξ) f θ^{'} + \frac{Nt}{Nb} θ^{″} = 0$ subject to the following boundary conditions(16) $\begin{matrix} η = 0, f = 0, θ = 1, Nb ϕ^{'} + Nt θ^{'} = 0 \\ η \to \infty, f^{'} = 0, θ = 0, ϕ = 0 . \end{matrix}$ where a prime denotes ordinary differentiation with respect to $η$ and the non-dimensional parameters in the aforesaid equations are as follows: $Nr = \frac{(ρ_{p} - ρ_{f \infty}) (C_{w} - C_{\infty})}{ρ_{f \infty} β (T_{w} - T_{\infty}) (1 - C_{\infty})}, Nb = \frac{ε β ({(ρ c_{p})}_{nf} D_{B} (C_{w} - C_{\infty}))}{{(ρ c_{p})}_{f} α_{m}}, Nt = \frac{ε {(ρ c_{p})}_{nf} D_{T} (T_{w} - T_{\infty})}{{(ρ c_{p})}_{f} α_{m} T_{\infty}}$ $ξ = \frac{x}{a}, Le = \frac{α_{m}}{ε D_{B}}, {Ra}_{x} = \frac{(1 - C_{\infty}) kg β ρ_{f \infty} (T_{w} - T_{\infty}) x}{μ_{nf} α_{m}}, {Pe}_{x} = \frac{Sin (\frac{x}{a})}{α_{m}}, Ra = \frac{{Ra}_{x}}{{Pe}_{x}} .$ where Le, Nr, Nb, Nt, ${Ra}_{x}$ , ${Pe}_{x}$ , and ξ are Lewis number, buoyancy ratio parameter, Brownian motion parameter, thermophoresis parameter, local Darcy-Rayleigh number, local Peclet number and the coordinate parameter, respectively. We note that the porosity (ε) is absorbed into the Nb, Nt and Leparameters, and therefore, it is not explicitly simulated in this study.

Quantities of practical interest in this problem are the local Nusselt number Nux, and the local Sherwood number Shx, are defined as(17) ${Nu}_{x} = \frac{{xq}_{w}}{k (T_{w} - T_{\infty})} {Sh}_{x} = \frac{{xq}_{m}}{D_{B} (C_{w} - C_{\infty})}$

Here, $q_{w}, q_{m}$ are the heat flux and mass flux at the surface (plate), respectively. Using (17) we obtain dimensionless versions of these key design quantities:(18) ${({Pe}_{x})}^{- 1 / 2} {Nu}_{x} = - θ^{'} (0), {({Pe}_{x})}^{- 1 / 2} {Sh}_{x} = - ϕ^{'} (0),$

In the present context, ${({Pe}_{x})}^{- 1 / 2} {Nu}_{x} and {({Pe}_{x})}^{- 1 / 2} {Sh}_{x}$ are referred to as the reduced Nusselt number and the reduced Sherwood numbers which are represented by $- θ^{'} (0) and - ϕ^{'} (0)$ , respectively. The set of ordinary differential Eqs. (13), (14), (15) is highly nonlinear, and therefore cannot be solved analytically. The finite-element method [40], [41], [42], [43] has been implemented to solve these nonlinear equations. The very important aspect in this numerical procedure is to select an approximate finite value of $η_{\infty}$ . So, in order to estimate the relevant value of $η_{\infty}$ , the solution process has been started with an initial value of $η_{\infty} = 4,$ and then the Eqs. (13), (14), (15) are solved together with boundary conditions (16). We have updated the value of $η_{\infty}$ and the solution process is continued until the results are not affected with further values of $η_{\infty} .$ The choice of $η_{\max} = 10 and η_{\max} = 6$ for temperature and concentration has confirmed that all the numerical solutions approach to the asymptotic values at the free stream conditions.

3. Numerical method of solution

3.1. The finite-element method

The Finite-element method (FEM) is such a powerful method for solving ordinary differential equations and partial differential equations. The basic idea of this method is dividing the whole domain into smaller elements of finite dimensions called finite elements. This method is such a good numerical method in modern engineering analysis, and it can be applied for solving integral equations including heat transfer, fluid mechanics, chemical processing, electrical systems, and many other fields. The steps involved in the finite-element method are as follows.

(i)
Finite-element discretization

In the finite element discretization the entire interval is divided into a finite number of subintervals and each subinterval is called an element. The set of all these elements is called the finite-element mesh.

(ii)
Generation of the element equations
- a.
  Variational formulation of the mathematical model over the typical element (an element from the mesh) is performed.
- b.
  An approximate solution of the variational problem is assumed, and the element equations are made by substituting this solution in the above system.
- c.
  Using interpolating polynomials the stiffness matrix is constructed.
(iii)
Assembly of element equations

By imposing inter element continuity conditions all the algebraic equations are assembled. This results in a large number of algebraic equations called global finite-element model and it represents the whole domain.

(iv)
Imposition of boundary conditions

The boundary conditions that represent the flow model are imposed on the assembled equations.

(v)
Solution of assembled equations

The assembled equations so obtained can be solved by any of the numerical techniques, namely the Gauss elimination method, LU decomposition method, etc. An important consideration is that of the shape functions which are employed to approximate actual functions.

4. Results and discussion

The system of Eqs. (13), (14), (15) together with the boundary conditions (16) is solved for different values of the parameters that describe the flow characteristics and the results are illustrated graphically and in tabular form. Numerical solution of the problem has been conducted (unless otherwise stated) at a point on the curved surface of the cylinder, i.e., $x = π$ , located at some distance from the lower stagnation point $(x \sim 0)$ . Selected graphical profiles are presented in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13. The results are compared with Gorla and Chamkha [44] for different values of Nr and with ξ = 0 and are shown in Table 1. Thus, it can be seen from Table 1 that the results are in good agreement with the existing results. The values of Nusselt number $- θ^{'} (0)$ and the values of Sherwood number $- ϕ^{'} (0)$ are shown in Table 2, for various values of Nr, Ra, Nb, Nt and Le at the cylinder surface. It is clearly observed from Table 2 that increase in buoyancy-ratio parameter (Nr) would decrease the magnitude of reduced Nusselt number whereas it increases the magnitude of Sherwood number. However, it is found that the heat transfer rates enhance and rate of dimensionless mass transfer also improves with the higher values of mixed convection parameter (Ra). This table reveals that with the enhancing values of thermophoresis parameter (Nt) depreciates the values of both reduced Nusselt and Sherwood numbers in the boundary layer region. The table also presents the effect of Brownian motion parameter (Nb) on dimensionless heat and mass transfer rates. It is clearly noticed that the Nusselt number and Sherwood number both increase with the increasing values of Brownian motion parameter (Nb). The results of the present study differ with the results reported in the literature [9], [10], [11] with respect to (Nb). They conveyed that both Nusselt and Sherwood numbers have decreasing tendency with the increasing values of (Nb). The noticed difference in the previous studies [9], [10], [11] is because of different physical range of parameters. Finally, the reduced Nusselt number enhances and the Sherwood number depreciates with the growing values of Lewis number (Le).

Figure 3. Concentration profiles for different values of Nr.

Figure 4. Temperature profiles for different values of Ra.

Figure 6. Temperature profiles for different values of ξ.

Figure 7. Concentration profiles for different values of ξ.

Figure 8. Temperature profiles for different values of Nt.