A comprehensive ship weather routing system using CMEMS products and A* algorithm

1. Introduction

There is a growing concern to reduce emissions in order to mitigate climate change. The environmental impact of transport is significant because it is the major user of energy. Shipping is the prevalent transport mode for overseas freight and is frequently recognized as a sustainable, energy-efficient and relatively environmentally friendly means of transport (DfT, 2004). However, shipping is still a substantial source of greenhouse gas emissions (Chapman, 2007). In this respect, the shipping industry is not exempt from the need to reduce emissions, and several initiatives have been taken by stakeholders and academics to promote sustainable growth (Goldsworthy and Goldsworthy, 2015; Kanellos et al., 2014; Wang et al., 2016; Zakaria et al., 2022; Zis et al., 2014a, 2014b). In the context, global decarbonisation target specific shipping sectors and the academia addresses several pertinent questions on information collection and planning routes (Wu et al., 2021; Zakaria et al., 2022; Zis et al., 2020b). In addition, a major factor of competitiveness in the maritime industry is the minimization of time and fuel consumption for ship routes. The emerging field of the autonomous ships also shows an increasing interest for optimization tools in the framework of performance management systems that includes analysis and real-time remote monitoring, hindcast/forecast wave conditions and make decision support (e.g. Ruth and Thompson, 2022; Zhao et al., 2022).

From the shipping industry point of view, the minimization of operating costs is a multi-faceted problem, which involves fleet management, vehicle routing problems such as scheduling or ship weather routing, among other strategies. Ship Weather Routing (SWR) is defined as the development of an optimum sailing course and speed for ocean voyages based on nautical charts, the forecasted sea conditions, the captain's experience and the individual characteristics of a ship for a particular route (Simonsen et al., 2015). Academic research has focused on ship routing optimization through pathfindingalgorithms (Hinnenthal and Clauss, 2010; Mannarini et al., 2016; Shin et al., 2020; Simonsen et al., 2015; Szłapczynska and Smierzchalski, 2009; Takashima and Mezaoui, 2009; Zhao et al., 2022; Zis et al., 2020a), which take into account meteo-oceanographic forecasts (i.e. wind, waves or currents predictions). Some of these contributions have been tested through a “proof-of-concept” based on oceanic distances (e.g. Hinnenthal and Clauss, 2010; Lin et al., 2013; Simonsen et al., 2015), but benchmarking tests have not been found in the literature covering different regional areas. A noticeable effort was made by (Mannarini et al., 2016), using an optimization algorithm based on the graph-search method with time-dependent edge weights in the Mediterranean Sea. In this respect, SIMROUTE presents a flexible structure, permitting all the CMEMS products (which cover all the world's seas) in a comprehensive design, which creates a fast-executing tool from the user perspective. SIMROUTE may enrich the ship weather routing field of investigation, which has been receiving increasing interest from academics in recent years (see review in Zis et al., 2020a). The code also provides a set of visualization tools for easy and direct inter-comparison of new SWR methods, which may include artificial intelligence and machine learning in the framework of autonomous ship development alternatives (e.g. Kuhlemann and Tierney, 2020).

The above-mentioned contributions have established an important source of knowledge for seeking efficient ship routes. With a comparable motivation in mind, we present SIMROUTE, an open-source, versatile and computationally efficient software for modelling optimal weather ship routes. SIMROUTE targets one of the aspirations of ship weather routing by minimizing time of navigation and, in consequence fuel consumption and emissions. SIMROUTE has been under active development since 2014 (Grifoll et al., 2018; Grifoll and Martínez de Osés, 2016) and offers modular functionalities including economic assessment, safety in navigation, and emissions estimations oriented to determine the benefit produced by the optimized route, including pre- and post-processing tools for direct and easy use. The Python programming language was chosen as the basis for SIMROUTE due to its flexible, free, and cross-platform-compatible nature. In addition, a MATLAB code version is available that is more oriented to academic purposes. The open-source code (GPL Licenses), together with support materials, is available in GitHub.com/ManelGrifoll/SIMROUTE. Code has been tested using Python 3 and the specific imported modules are included in the headers of the code. This package also provides plotting tools and oriented modules for ship emission or the assessment of safety conditions during navigation. The objective of this contribution is to present the conceptualization, software structure, formulation and the main features of the SIMROUTE, illustrated by examples, as an open-source software for the scientific and teaching community.

The main methodologies used in SWR include the isochrone method (Hagiwara, 1982), dynamic programming (Shao et al., 2012), path-finding algorithms in grid-based approach (Mannarini et al., 2016) and artificial intelligence (Maki et al., 2011) among others (Walther et al., 2016). suggest that grid-based approaches are only suitable for short routes (i.e. coastal shipping) because of its computational efficiency. The improbable smoothness of the solutions is one of the potential drawbacks. However, SIMROUTE uses grid-based approaches A* as a trade-off between accuracy and computational time assuming standard computational resources. Other, conceptual assumptions have been considered in the development of the SIMROUTE software. SIMROUTE assumes that the weather effect increases the total resistance acting in a vessel. Therefore, avoiding bad weather conditions will reduce the sailing time. Also, it means that reducing the sailing time will reduce the fuel consumption and the economic cost per voyage. In consequence, SIMROUTE optimizes the sailing time, taking into account eventual speed reduction due to the waves. In order to evaluate the benefit of the optimization, the minimum distance route is also provided by SIMROUTE.

This paper is organized as follows: after the introduction (Section 1), a SIMROUTE description, methods and accuracy test are presented in Section 2. Section 3 shows test cases also included in the repository. Finally, Section 4discusses the results and contextualize the work and Section 5 includes concluding remarks, identifying future areas of research.

2. Materials and methods

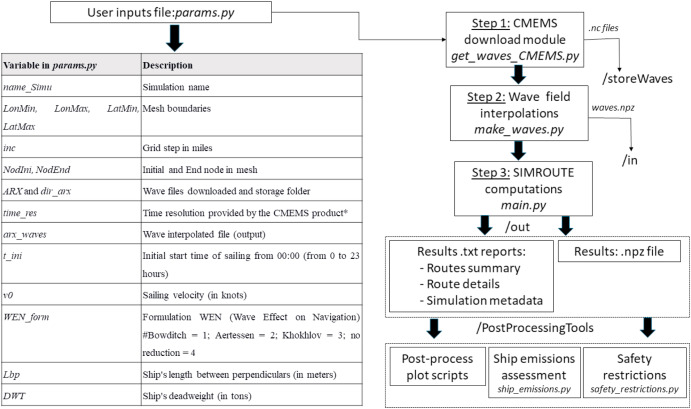
The software structure consists in a sequential execution of Python scripts. A flow chart to guide SIMROUTE users is shown in Fig. 1, including the folder organization (i.e. in/, out/ and /storeWaves) and the post-processing tools. Input variables are included in a unique .py file: params.py. This set-up file establishes the characteristics of the mesh, period of simulation, wave effect on the navigation model and ship velocity, among other parameters (see Fig. 1 for a short description). The code execution is designed following three steps of .pyscripts. The script get_waves_CMEMS.py is a pre-processing file that downloads sea surface waves variables in daily files configuration using motuclient from CMEMS repository. Secondly, make_waves.py interpolates the wave information into a specific mesh generated as a function of the boundaries and the mesh increment size. Finally, main.py executes the optimization algorithm, resulting in two alternatives: an optimized route and a minimum distance route.

2.1. Wave information source

The wave information files are downloaded from the European Union's Earth observation programme Copernicus. The Copernicus Marine Environment Monitoring Service (CMEMS) provides full, free and open access data and information related to the physical state of the global ocean. Several ocean wave products are provided in the CMEMS catalogue (European Commission, 2021) covering different geographical regions. Fig. 2 shows the regional coverage of the different products excluding the Arctic and Global products also used in SIMROUTE. The get_waves_CMEMS.py script downloads the wave files in netcdf format provided by different CMEMS products (forecasting data sets) as a function of a specific flag (wave_prod). This script also uses the param.py to establish and trim the geographical area of the wave fields. Downloaded wave files are stored in storeWaves/in daily format. The products available in the SIMROUTE structure are summarized in Table 1. Motuclient is used to extract and download data through a Python command line. This client enables the handling and transformation of huge volumes of oceanographic data without performance collapse and is available at the GitHub platform.

Table 1. CMEMS products included in SIMROUTE system. * One-hour resolution for all domains except GLOBAL (3 h).

CMEMS Id.	Geographical covering	Spatial Resolution	wave_prodFlag	Reference
GLOBAL	Global Ocean	0.083° × 0.083°	1	Ardhuin et al. (2010)
MEDSEA	Mediterranean Sea	0.042° × 0.042°	2	Korres et al. (2021)
IBI	Iberia-Biscay-Irish Regional Seas	0.05° × 0.05°	3	European Commission (2021)
AENWS	Atlantic European North West Shelf Seas	0.03° × 0.014°	4	European Commission (2021)
BLACK SEA	Black Sea	0.037° × 0.028°	5	(Staneva, J., Behrens, A., Ricker, M., & Gayer, 2020)
BALTIC SEA	Baltic Sea	2 km × 2 km	6	European Commission (2021)
ARCTIC OCEAN	Arctic Ocean	3 km × 3 km	7	European Commission (2021)

2.2. Mesh and wave effect on navigation

The computational mesh is established as a function of the grid resolution (incvariable) and the boundary limits defined in params.py. Once the mesh is obtained, the nodal connections possibilities are increased to enable smooth destinations composed from a sequence of edges. SIMROUTE nodes are connected by 48 edges, allowing 48 distinct directions per node (see Fig. 3) and enabling a smoothing of the sailing routes alternatives (Cheung, 2018) This enables angular courses of a range of 3.2° ‒ 14.0° resolution to be obtained. Singular points on the mesh boundaries and corners are treated particularly to avoid non-defined mesh points when node searching. The initial and final nodes are defined also in params.py (see input variables in Fig. 1). These nodes are referred to the mesh computed previously; so a script is provided (i.e. find_ports.py) to convert the coordinates of the initial and final points, including checking to determine if the node is sea or land. Also, additional information is provided by this script in a command prompt for an iterative process on searching the initial and final nodes on the sea. The discrimination between either sea or land is given by the wave fields interpolated. Fig. 4 shows the mesh generated which the routes (i.e. minimum and optimal) are computed and an example of the interpolated significant wave height.

Because the CMEMS meshes and SIMROUTE mesh differ, the wave parameters (wave direction, wave period and significant wave height) from the CMEMS product are linearly interpolated in the computational mesh (see Fig. 4). Time resolution data are provided from CMEMS products (i.e. hourly or 3-hourly). The wave direction requires a particular interpolation based on Cartesian decomposition. The interpolated wave fields are saved on an intermediate file (waves.npz by default defined at params.py) in the in/ folder. Route possibilities during ship routing computations are linked to the availability of wave information.

The wave, or sea state, parameters are essential in studies related to evaluations of the safety and fuel efficiency of marine designs and operations (Nielsen, 2021). In this contribution, the parametrization of the wave effect on navigation is based upon three methods, namely, Mannarini (suggested by Bowditch), Aertssen and Khokhlov (suggested by Lubkovsky) (Aertssen, 1975; Lubkovsky, 2009; Mannarini et al., 2013). All three methods depend on the significant wave height as well as the wave direction (see Appendix I). However, Aertssen's method also takes into account the ship's length dimension, whereas Khoklov takes into account the deadweight of the ship (Borén et al., 2019) showed the discrepancies when using different calculation methodologies on ship routing in terms of the sailing time during storm episodes (large significant wave height). The Aertssen and Khokhlov methods give very similar results whereas the first method showed considerably higher values of ship velocity penalization due to waves. The ship-wave encounter direction is computed using an edge-based spherical method to preserve the coordinate system of the mesh.

2.3. Optimization algorithm

The pathfinding algorithm used is the A* algorithm due to its simplicity and efficiency in computational time. This algorithm is applied to a gridded scheme where each grid point (node) is connected to a set of adjacent points. To each connection (edge), a weight related to the distance is assigned. The great circle (orthodromic) track is used for the spherical coordinates of the grid nodes. A* solves problems by searching among all possible paths to the solution (goal) for the one that incurs the smallest cost (least distance travelled, shortest time, etc.), and among these paths, it first considers the ones that appear to lead most quickly to the solution. A* is formulated in terms of a weighted mesh: starting from a specific node of the mesh, it constructs a tree of paths starting from that node, expanding the paths one step at a time, until one of its paths ends at the predetermined goal node. At each iteration of its main loop, the A* algorithm needs to determine which of its partial paths to expand into one or more longer paths. It does this based on an estimate of the cost (in our case, the travel time) to reach the goal node. Specifically, A* selects the path that minimizes the total cost function $f (N_{n})$ :(1) $f (N_{n}) = h (N_{n}) + \sum_{i = 1}^{n} g (N_{i})$ where $N_{i}$ denotes the ith nodes along the path candidate, $g (N_{i})$ the cost of going from $N_{i}$ to the parent $N_{i} - 1$ , $h (N_{n})$ is a heuristic that estimates the cost of the cheapest path from n to the goal (see Cheung, 2018 for a complete description). The heuristic allows longer paths to be eliminated progressively during the search. For the algorithm, to find the actual shortest path, the heuristic function must be admissible, meaning that it never overestimates the actual cost to get to the nearest goal node. The heuristic function used in SIMROUTE is the travelling time associated with the minimum distance between the origin and destination. When $h (N_{n}) = 0$ , A* reduces to the Dijkstra algorithm.

The accuracy of A* implementation is tested by comparing with the orthodromic (or great-circle) distances. Different tests have been carried out in order to evaluate the error of the recovered path versus the analytical formula of the orthodromic distance in terms of the distance travelled. Four tests have been defined considering different positions (latitude and longitude) for the start and end point (see Table 2). Fig. 5 shows the shortest path estimated by A* on the surface of a sphere for each of the test cases. The mesh grid is equal to 15 miles, substantially larger than the test cases shown in the next section. The distance travelled computed by A* and the differences obtained compared with the orthodromic distance are shown in Table 2, in which differences less than 0.4% are obtained. The results guarantee a proper application of the shortest path algorithm used (i.e. A*) embedded in SIMROUTE and its application for SWR problems.

Table 2. Numerical results of the orthodromic distance and shortest path distance (in nautical miles, nmi) comparison exercise shown in Fig. 5. The shortest path distance is estimated by A* implemented in SIMROUTE code.

Case	Initial point (lon,lat)	Final Point (lon, lat)	Orthodromic Distance	Shortest path Distance	Difference in miles (Mean Absolute Percentage Error)
1	0°, 10N°	120°E, 10°N	7023.01	7038.25	15.24 (0.21%)
2	0°, 20N°	120°E, 20°N	6536.24	6549.36	13.12 (0.20%)
3	0°, 30N°	120°E, 30°N	5830.85	5845.51	14.66 (0.25%)
4	0°, 40N°	120°E, 40°N	4987.29	5005.56	18.27 (0.37%)

Table 3. Travel times (in hours) and distances (in nautical miles) and additional information of the CMEMS product test cases included in the repository. Min.: minimum distance route, Opt.: optimized route. Hs is the significant wave height.

Test case	CMEMS product	Min. Dist. time	Opt. time	Min. distance	Opt. distance	Max(Hs) Opt/Min (in m)	Emissions Savings (Min vs Opt)	Period of analysis	File in SIMROUTE repository
R1	MEDSEA	33.29	27.33	386.30	390.63	5.26/5.34	28.69%	13th-14th/01/2021	params_MEDSEA_2.py
R2	AENWS	38.64	37.85	539.12	544.38	4.23/4.17	4.47%	18th-19th/02/2020	param_AENWS.py
R3	GLOBAL	66.48	62.25	984.93	986.47	2.54/5.28	13.25%	18th–20th/04/2020	param_GLOBAL.py
R4	IBI	26.10	24.13	249.07	287.42	5.68/7.04	15.05%	16th-17th/02/2020	param_IBI.py
R5	GLOBAL	61.40	60.12	912.16	917.77	8.70/10.13	5.02%	8th-10th/08/2019	param_GLOBAL_2.py
R6	MEDSEA	16.93	14.97	151.38	161.56	6.95/6.85	16.14%	20th-21st/01/2020	params_MEDSEA.py
R7	BALTIC	17.47	17.43	266.64	266.88	2.73/2.86	0.61%	5th-6th/02/2020	param_BALTIC.py
R8	GLOBAL	187.04	183.60	2687.2	2725.9	6.00/6.44	4.42%	18th–25th/01/2020	param_GLOBAL_3.py

2.4. Results files and post-processing

The SIMROUTE results information consists of two sets of files including the final and intermediate results and appropriate information to ensure an eventual simulation replication (see Fig. 1). On the one hand, a set of ASCII files (.txt) includes information of the cost function optimized (sailing time and distance including wave effect on navigation), minimum distance route, great circle distance and information to the start and end point, including departure time and mesh information (Res_route.txt). Metadata_route.txt includes information to replicate the simulation (e.g. wave fields, wave effect on navigation formulation, etc.). Finally, the file Route_route.txt includes the nodal information of the optimized route (longitude, latitude and wave conditions per each node visited by the optimized route). On the other hand, the .npz file (a file format by numpy Python library that provides storage of array data using gzipcompression) is provided to allocate all the input/output variables of the simulation, including wave interpolated information. The simulation name, which is linked with the output file names, is provided also in params.py (see Fig. 1).

Post-processing tools are based on the .npz result file to ensure a decoupling of the simulation and post-processing analysis. Different graphical tools are oriented to provide comprehensive results including Lambert and Plate-Carrée projections. Also, the synchronous plotting or waves fields and routes are available using the Cartopy python library. Examples of post-processing tools based on test cases are displayed in Fig. 6, Fig. 7, Fig. 8.

2.5. SIMROUTE for academic purposes

From the academic point of view, ship weather routing and marine environment protection are specific topics in all Maritime Academies and Universities and related to the Seafarers’ Training, Certification and Watchkeeping (STCW) Code (International Maritime Organization, 2010), as a part of mandatory training. Castells-Sanabra et al., 2019 identified which STCW competences the learner will achieve using SIMROUTE software, providing skills of ship routing optimization, to assess the impact of the meteo-oceanographic variables on ship navigation and to highlight the relevance of ship routing in terms of the sailing time, safety, fuel consumption and harmful emissions for the environment. Then, two academic modules were developed: i) safety restrictions and dangerous motions, and ii) ship emissions assessment. The SIMROUTE software is available for the academic community, together with comprehensive documentation and test cases oriented to guide teachers.

2.5.1. Safety restrictions module

The susceptibility of a vessel to dangerous phenomena will depend on the stability parameters, ship speed, hull shape and ship size. This means that the vulnerability to dangerous responses, including capsizing, and their probability of occurrence in a singular sea state may differ for each vessel. During navigation, unstable motions (surf-riding and parametric rolling) may be encountered, which may lead to a cargo or equipment damage and the unsafety of the persons on board. Safety restrictions to avoid surf-riding and parametric rolling are implemented into SIMROUTE according to the guidelines of the International Maritime Organization (International Maritime Organization, 2007) in order to know and avoid all the dangerous nodes from the route (see formulation in Appendix II). safety_restrictions.py is a post-processing tool to identify both dangerous unstable motions in the optimized route (see example in Fig. 9).