Rotation of Biological Cells: Fundamentals and Applications

1. Introduction

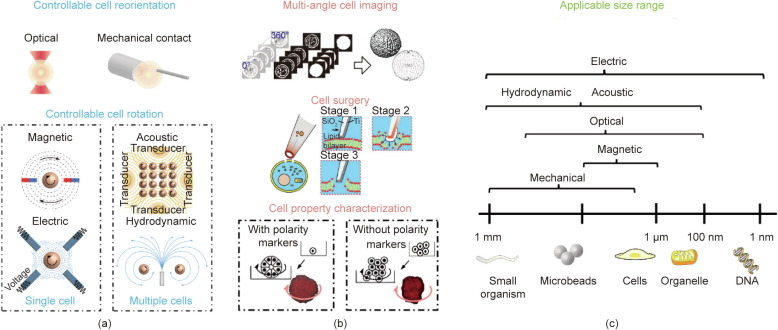
Cell rotation is a cell manipulation technique that enables three-dimensional (3D) cell imaging [1], [2], [3], [4] and observation from a specific angle [5], [6]. The rotational motion [7], [8] of cells under certain conditions (e.g., electrorotation (ROT)) is an important label-free biomarker for cell discrimination. The approaches used for cell rotation can be divided into six groups according to the applied mechanisms: optical field [9], [10], mechanical contact [11], magnetic field [12], [13], electric field [14], [15], acoustic field [16], [17], and hydrodynamic field [18], [19] methods, as illustrated in Fig. 1(a).

Cell populations are heterogeneous, and even cells of the same type differ from each other, since living biological cells vary in their shapes, sizes, and other biophysical features [20]. It is of great importance to detect and visualize the biological dynamics of cell surface morphologies in biological, medical, and clinical applications [21]. However, confocal microscopy, a commonly used optical technique for cell image acquisition, is limited to transparent samples and certain visible angles, and has limited resolution in the XY plane (100 nm) and Z direction (200 nm). In comparison with other available setups, such as 3D structured illumination microscopy (SIM) [22], [23], [24], on-chip cell rotation under a confocal microscope is a more affordable way to enhance spatial resolution and achieve 3D visualization of cell dynamics, due to its low reagent consumption, fast sample processing, high integration, portability, and low cost. For example, on-chip cell rotation activated by acoustic tweezers [25] has been applied to build high-resolution 3D optical reconstructions under an ordinary confocal microscope with a visible angle of up to 140° [1]. Furthermore, the integration of optical tweezers (OTs) [26], [27] in microfluidic devices further extends the visible angle of cells to 180° and enables the visualization of cells from a specific angle in a process known as cell reorientation. Due to its capability to reorientate and visualize cells, optical-activated on-chip cell rotation has enabled a wide range of applications in cell surgery processes (e.g., cell injection, intracellular structure biopsy, and organelles extraction), in which target cells are required to be properly orientated in order to mitigate side effects on cell viability [28], [29]. For example, in mammalian oocytemanipulation, the polar body of the oocyte must be rotated away from the injection site to prevent damage to the spindle, which is close to the polar body inside the oocyte [3], [30]. Other examples include the necessary, precise control of cell orientation in order to avoid damage to organelles in the cell and thus increase the success rate of micromanipulation [31], [32].

The rotational motions of cells of different shapes or types vary even under the same conditions, so cell rotation can be used to characterize cellular properties and status in relation to the chemical composition or physical features. In a breast cancer study [33], the rotational motion of cancer cells was found to be distinguishable from that of normal cells having spherical shapes. A stable rotation, or so-called coherent angular motion, was necessary for normal cells to form spheres. However, the study pointed out that the loss of polarity prevented cancer cells from forming spheres, which is one of the earliest signs of malignancy and which leads to rotational motion disorders, as shown in Fig. 1(b) [33], [34], [35]. In addition, the physical features and chemical composition of cells (e.g., the dielectric properties of cells) are accessible from cellular rotational motion based on lab-on-a-chip techniques. For example, Han et al. [15] proposed a microfluidic device with a nonuniform electrical field, which was applied to analyze the rotating patterns of target cells (e.g., rotation speed and direction), and Huang et al. [36] demonstrated its capability for cell characterization and discrimination. The controllable rotation of cells and microbeads is a tool that allows researchers to uncover the mechanical properties of target components. For example, the rotation of magnetic beads under a rotating magnetic field enables the high-speed measurement of the structural dynamics of DNA gyros [37], [38]. Similarly, acoustic-field-based rotation is preferred for cell characterization due to its capability to excite the rotation of numerous particles with a relatively large output force [39]. Rotation strategies based on external acoustic fields also enable the parallel analysis of multiple bio-samples [40], [41] with either open or closed microfluidic devices, although the stability of multi-cell control needs further improvement.

Although there are several on-chip methods for cell rotation, each method has a limited applicable range of cell sizes, as summarized in Fig. 1(c). For small organisms or microbeads, three types of manipulations (mechanical, acoustic, and hydrodynamic) are available, with applicable sizes of up to 1 mm. Optical field approaches are suitable to rotate cells or organelles varying in size from 0.1 to 100 μm, due to the low output force. Magnetic field approaches are primarily used to rotate magnetic beads with sizes ranging from 1 to 10 μm. Lastly, electric field approaches can be used to rotate samples with various sizes ranging from 0.001 to 1000 μm. The spatial resolutions of mechanical approaches and optical approaches are likely to be up to 10 μm and 0.1 μm, respectively (resolutions are summarized later in Section 4). Besides, both techniques enable the precise control of rotation angle, but they also have limitations in real applications. Mechanical contact approaches carry a high risk of injuring soft cell membranes and impairing cell viability, while OTs with high optical intensities (normally > 105 W·cm−2) show a tendency to kill cells or cause optical damage, limiting their applications.

This review aims to analyze representative academic studies utilizing six major groups of approaches to rotation (either direct contact or non-contact approaches, as shown in Fig. 1(a)). We then provide additional details about the merits and demerits of each approach under different conditions and discuss possible future trends in this field. We have classified the approaches in these six groups into two classes based on the purpose of rotation: cell reorientation and cell rotation (Fig. 1(a)). More specifically, controllable cell reorientation aims to rotate cells precisely toward a specific angle, and is mainly performed using an optical field or mechanical contact. In contrast, controllable cell rotation aims to rotate the cell at a steady speed; in this case, a magnetic field or an electric field is commonly used to rotate single cells, while acoustic field or hydrodynamic field approaches mainly focus on the rotation of multiple cells in parallel.

2. Controllable cell reorientation

Precise cell orientation is necessary for cell microinjection, for the precise delivery of substances into cells, and for the study of cell transfection, signaling pathways, and organelle functions [42], [43], [44], [45]. To enable injections at specific locations of an embryo and to avoid any damage to specific internal organelles, it used to be necessary to manually adjust the position and posture of the cells, which was limited by low efficiency and a low success rate [31]. Currently, automated processes are gradually replacing the existing manual reorientation strategies. For example, a closed-loop control manipulator driven by a direct current (DC) motor [46], [5] can provide repeatable and fast positioning of cells with a spatial resolution greater than 0.1 μm, which is difficult to achieve by manual operation.

2.1. Mechanical contact approaches

Mechanical contact approaches utilize tools (e.g., micropipettes with certain fabrication specifications) mounted on a manipulator that directly interact with the target cell to achieve the translocation or reorientation of cells. Compared with manual reorientation approaches that require highly skilled operators, the use of manipulator and control systems enables mechanical contact approaches to simplify operation processes and reduce cell damage [5], [4], [47].

The great majority of mechanical contact approaches aim to replace operators with micro-robotics (Table 1 [46], [4], [47], [48], [49], [50], [51], [52]). For example, Wang et al. [46] proposed a method for the real-time recognition and reorientation of embryos, in which the reorientation of target cells is powered by frictional force related to cellular deformation (Fig. 2(a)), with 2° of rotational freedom and a success rate of up to 97.50%. Furthermore, as shown in Fig. 2(b), a push force controlled by programs [48] can orientate cells with a rotation angle error of 5°, although the degree of freedom (DOF) of this approach is limited to one. Alternatively, as shown in Fig. 2(c)), multiple micropipettes can function as fingers [4], where the target cell is held by one “finger” and rotated by another one, which reduces the rotation error to around 1.2°. Based on the minimum rotational force model, a varying torque is applied to rotate target cells according to the cellular deformation, which successfully minimizes the side effects on cell viability, albeit with some cost to manipulation efficiency. Recently, an improved method [49] has been developed that optimizes the direction of the injection micropipette and significantly reduces the processing time to 5 s per cell. Meanwhile, with two micropipettes, the system [50] can achieve a success rate as high as 92.5% with a maximum error of 0.3°.

Table 1. Summary of publications describing the development of cell reorientation using mechanical contact approaches.

Authors	Rotational DOF	Speed	Rotation angle error	Success rate	Rotating object	Application
Zhao et al. [4]	1	28.6 s per cell	1.2°	93.3%	Porcine oocytes	Nuclear transplantation
Wang et al. [50]	3	31 s per cell	0.3°	92.5%	Zebrafish embryos	Cellular structure recognition
Wang et al. [46]	2	In-plane: 1 s per cell Out-of-plane: 4 s per cell	0.5°	97.5%	Zebrafish embryos	Cellular structure recognition
Wang et al. [47]	3	Out-of-plane: 2 s per cell	—	96.25%	Mouse oocytes	Polar body biopsy
Zhuang et al. [51]	2	44 s per larva	0.5°	z-axis: 94%; x-axis: 100%	Zebrafish larva body	Organs injection
Ajamieh et al. [48]	1	—	5°	—	Mouse embryos	Cell biopsy procedure
Zhao et al. [49]	1	23.6 s per cell	—	93.3%	Porcine oocytes	Nuclear transplantation
Aishan et al. [52]	3	—	0.72°	—	Xenopus oocytes	Full surface cell observation

DOF: degree of freedom.

At present, mechanical contact-based methods are widely used for cell reorientation, although they carry the risk of physical damage and undesired stimulation [55]. These methods allow a relatively high spatial resolution (up to 0.01 μm) for particle reorientation and manipulation, ensuring the repeatability of similar orientational manipulations. Moreover, a rotation accuracy of 0.3° has been achieved with mechanical contact-based techniques, which is much smaller than that of other manual methods (8.3°) [4]. Although many improvements of the control system have been made to enhance the stability and precision of the operation, the minimum applicable size is limited to about 100 μm.

Compared with the direct rotation of cells, rotational control by means of microfluidic devices is much simpler and more accessible for cell observation. Aishan et al. [52] established an observation platform by fabricating an all-closed glass chamber through combining the techniques of thermal-expansion-based glass-dome-structure fabrication [53] with ultra-thin glass fusion bonding [54], in which high-precision control of the observation angle was achieved with an error of 0.72°. The target cell was placed in a closed chamber to reduce the risk of outer contamination during observation and to eliminate possible physical damage caused by stiff actuators; however, an all-closed microenvironment limits other applications such as cell surgery.

2.2. Optical field approaches

OTs have become one of the most popular optical-field-based techniques applied in cell rotation, after first being investigated by Ashkin et al. [56], [57]. A highly focused laser beam functions as an optical trap that applies trapping force and torque to particles of interest, allowing the label-free manipulation of captured micron-sized dielectric particles [58], [59], [60], [61], [62]. In contrast to mechanical contact approaches, the stiffness and magnitude of the forces applied by OTs vary with the intensity of the laser beams, and the trapping forces of OTs vary in a range from femto-newtons to nano-newtons, which makes them well-suited for capturing micron-sized particles with different sizes and weights [63], [64]. Furthermore, dual-beam optical traps have shown the capability of cell reorientation [65], [66], and their self-organizing property [67], [68] has been verified using counter-propagating laser beams. The selection of appropriate laser beams for the manipulation of red blood cells and cancer cells was described in the study by Kreysing et al. [69] and Dasgupta et al. [70]. In addition, in the past research [71], [72] of our team, we found that a focused femtosecond laser beam can induce impulsive forces without any thermal effects, enabling non-contact cell manipulation. Although few studies have been published on cell rotation by OTs, this topic may become a research trend.

2.2.1. Optical trapping forces and cell refraction

Optical trapping forces, which are generated as a result of the interaction between a focused laser and the trapped object, enable the rotation of target cells via OTs under an ordinary commercial microscope. A typical apparatus (Fig. 3(a)) used for optical manipulation mainly consists of some optics components, such as a microscope with a bright field or illumination, a high numerical aperture (NA) objective lens, and a condenser detection lens. Typically, the wavelength of the applied laser beam is near-infrared, which avoids various kinds of biological photo-damage and can easily be incorporated with other visible light forms [73] in the imaging system. Furthermore, a trapping laser can be coupled with a single-mode optical fiber to produce a clean beam profile, and can then be split by a spatial light modulator (SLM) into multiple simultaneous trapping beams. Therefore, the manipulation of multiple cells can be performed in parallel utilizing holographic OTs.

Fig. 3(b) illustrates the changes in the propagation path of laser beams before and after entering the cell, and shows the momentum transformation that occurs at the cellular surface. Based on Snell’s law, the refraction alters the propagation direction of two incoming laser beams, ki,1 and ki,2. The momentum relation between the incoming and outgoing beams, ks,1 and ks,2, can be formulated as follows.(1) $\{\begin{matrix} Δ k_{1} = k_{i, 1} - k_{s, 1} \\ Δ k_{2} = k_{i, 2} - k_{s, 2} \\ Δ k = Δ k_{1} + Δ k_{2} \end{matrix}$

Following momentum conservation, the momentum of both laser beams, Δk1and Δk2, is transferred onto the target cell. As a result, trapped particles experience a compensatory momentum Δk, pointed toward the focal point, as shown in Fig. 3(b). Due to the effect of scattering force, OTs are capable of capturing dielectric microparticles through a highly focused laser beam and trapping them at a point behind the focal plane (Fig. 3(b)).

2.2.2. Optical tweezers for cell reorientation

Figs. 3(c-I–III) show schemes for the direct optical rotation of cells, a method that has attracted great attention due to its high precision [9], [67]. Xie et al. [74] recently reviewed the rapid development of robot-aided OT systems over the past decades, which illustrates the operation of multiple laser beams for cell rotation. Aided by a closed-loop system, Xie et al. [5], [75] also realized the rotation control of target cells in either the XY plane or the YZ plane, by controlling both laser tweezers’ trajectories or distance (Figs. 3(c-II–III)). The robot-aided approach is fairly reliable and is applicable for more demanding tasks, such as the spin and orbital rotation of cells. In a study by Chen et al. [65], two OTs with 10 μm displacement could rotate red blood cells at an approximate speed of 72.2 (°)·s−1; however, when the displacement increased to 15 μm, the cells were found to move along an elliptical orbit (150.7 (°)·s−1) while self-rotating at 57.3 (°)·s−1.

One limitation of OTs is the optical damage that they cause. A study pointed out that a relatively high optical peak intensity (> 105 W·cm−2) [76] is necessary to generate stable traps; however, as shown in Table 2 [5], [65], [75], [77], [78], [79], [80], such highly intensive laser irradiation [81] may result in photo-damage to cells or tissues [82]. More specifically, direct laser irradiation may lead to various side effects at the single-cell level, such as local overheating [83], changes in cell metabolism [84], molecular photo-conformation [81], [85], protein denaturation [86], and photomechanical stress [87], all of which eventually cause the loss of cell viability. Thus, despite the fact that OTs provide very precise rotation control, photo-damage must be taken into consideration. Other adverse impacts of direct laser exposure include Brownian motion and thermal disturbance [88], which can further disturb the trapped particles.

Table 2. Summary of publications describing the development of cell rotation using optical field approaches.

Authors	Method	Rotational DOF	Angular velocity ((°)·s−1)	Photo-damage occurrence rate	Optical beam number	Rotating object	Application
Chowdhury et al. [77]	Pushing-based method	1	—	0	2	Dictyostelium discoideum cells	Migration study of cells
Chowdhury et al. [78]	Topological gripper	1	14.32	33%	3–6	Dictyostelium discoideum cells	Noninvasive transportation of cells
Thakur et al. [79]	Pushing-based method	1	—	0	2	Yeast cells	Cell translocation
Cheah et al. [80]	Topological gripper	1	—	33%	6	Silicon beads	Grasping and manipulating a microscopic particle
Xie et al. [75]	Direct rotation	2	8.59	67%	2	Yeast cells	Single-cell surgery
Chen et al. [65]	Direct rotation	2	Spin: 72.19; orbital: 151.26	67%	2	Red blood cell	Simultaneous spin and orbital rotation
Xie et al. [5]	Direct rotation	2	9.74	67%	2	Acute promyelocytic leukemia cells	Cell surgery

Alternatively, indirect optical rotation can avoid these side effects of direct laser exposure and mitigate photo-damage. Table 2 summarizes the photo-damage occurrence rate for each optical rotation approach. As shown in Figs. 3(c-IV–VI), these approaches can be divided into three categories: topological grippers, pushing-based methods, and attached particles. For example, topological grippers [5], [78], [80] are formed by several beads (Fig. 3(c-IV)) and controlled by multiple laser beams; they can reduce the laser exposure on cells by 90%. Some cells are still sensitive to the remaining 10% laser exposure, and their physiological characteristics will change during topological gripper use. This issue has been dealt with by placing an intermediate bead between the target cell and the optically manipulated beads [77], [79], as shown in Figs. 3(c-V–VI), where the optically trapped beads act as a non-contact actuator and eliminate almost all side laser effects on the target cells.

Another limitation of OT rotation is the lack of selectivity and exclusivity. In other words, OTs will trap any dielectric particle near the laser focal point [89]. Relatively low concentrations of cells, therefore, are required in order to prevent the collision and capture of additional particles. Significant efforts [90], [91], [92] have been made to attenuate the influence of high concentration on cell manipulation, such as through trajectory planning algorithms to optimize cell manipulation. In addition, the applications of optical-based rotation techniques are limited by the low output forces of OTs. For example, single-beam optical rotation can generate a trapping force that is only sufficient to rotate a cell of about 10 μm, and is insufficient to rotate larger ones such as oocytes (> 100 μm) [93].

In this section, we reviewed two rotation techniques—robot-aided mechanical rotation and optical rotation—for cellular reorientation with precise angle control (not at the rotation speed). Controllable cell rotation is necessary for some other cases, such as analysis of the rotational characteristics of cells and 3D optical reconstructions; this topic is reviewed below.

3. Controllable cell rotation

Herein, “cell rotation” refers to the rotation of target cells at a steady and controllable rate. Precise single-cell rotation is important for many applications in biotechnology, such as cell characterization [94], drug discovery [95], [96], tumor heterogeneity profiling [97], [98], and cell imaging [1], [10]. In this section, cell rotation is actuated by non-contact physical fields, such as electric, magnetic, acoustic, and hydrodynamic fields (Fig. 1(a)).

3.1. Electric field approaches

Cells can rotate in a rotating electric field in which the rotational torque is generated by the phase difference between the dipole moment of the cell and the rotating electric field. Furthermore, in a non-rotating electric field, rotational motion can be stimulated by an uneven or time-varying electric field. In an alternating current (AC) field, the electric torque, which is induced by dielectrophoresis (DEP), is able to manipulate particles ranging from a few nanometers to hundreds of microns in size by altering the field strength, frequency, or electrode geometries. DEP [99], [100], [101] has many unique features, including low cost, high efficiency, and a low injury rate. In addition, different particles may respond differently to an electric field. For example, the rotation direction of Janus particles is related to the AC frequency [102], which causes the particles to co-field rotate at a low AC frequency and vice versa. Meanwhile, DEP is capable of distinguishing and separating different types of cells based on the motion of the cells, which is related to the cells’ dielectric properties.

3.1.1. Dielectrophoresis and ROT

The fundamentals of DEP forces have been well described in the literatures [99], [100], [101], [103]. Theoretically, a cell can be polarized in a nonuniform electric field [104]. If it is more polarized than the medium, a net force toward the strong electric field is generated, known as positive DEP, and vice versa. Based on this theory, Chow et al. [105], [106] designed a liquid metal-filled multifunctional micropipette and achieved four-dimensional (4D) single-cell rotation (Fig. 4(a) [106]) by forming an unbalanced force torque at different positions on the cell surface.

A homogeneous spherical cell with radius R in a uniform electric field E is equivalent to a dipole with a moment phasor (Fig. 4(b) [7]). In a DEP biochip [107], the dipole will interact with the external electric field and generate a DEP force, as expressed below:(2) $\{\begin{matrix} F_{D E P} = 2 π R^{3} ∙ ε_{m} ∙ Re (f_{C M}) ∙ \nabla E^{2} \\ f_{C M} = {(ε}_{p}^{*} - ε_{m}^{*}) / (ε_{p}^{*} + 2 ε_{m}^{*}) \\ ε^{*} = ε - i \frac{σ}{ω} \end{matrix}$ where the DEP force (FDEP) is proportional to the real part of the complex Clausius–Monssotti factor (fCM), and $ε_{m}$ and $ε_{p}$ are the medium permittivity and particle permittivity, respectively. The * represents the complex variable, and the complex permittivity, $ε^{*}$ , is linearly associated with the substance permittivity ( $ε$ ) and angular frequency ( $ω$ ) of the rotating field. Additionally, Re(∙) stands for the real part of a complex variable, $σ$ is the medium conductivity, and i is the imaginary unit.

In a rotating electric field, cell rotation can be derived by the ROT torque (TROT).(3) $T_{R O T} = - 4 π R^{3} ∙ ε_{m} ∙ I m (f_{C M}) ∙ {|E|}^{2} ∙ z$ where the TROT is proportional to the imaginary part of the complex Clausius–Monssotti factor, $z$ is a unit vector normal to the surface of the electrode, and Im(∙) stands for the imaginary part of a complex variable. The phase delay between the electric dipole and the external field results in a relative lag angle between the two rotational torques. In a steady-state equilibrium condition, the rotation speed or angular velocity [15] can be defined as follows:(4) $α_{R O T} = - \frac{ε_{m ε} ξ {|E|}^{2}}{2 η} I m (f_{C M})$ where the rotation speed ( $α_{R O T}$ ) is proportional to the imaginary part of the complex Clausius–Mossotti factor, and $ξ$ is a scale factor [108], [109] (typically a constant) related to the viscosity ( $η$ ) and the electric field strength.

3.1.2. Electric field for cell rotation

Walid Rezanoor and Dutta [110] realized cell rotation in a stationary electric field by an AC signal with time-varying frequency, in which a nonuniform electric field was generated to polarize the target cells (Fig. 4(c)). They found that the rotation speed in a stationary electric field is tightly associated with the AC frequency, although the underlying mechanism is not fully understood. Furthermore, the steady rotation of a cell is not only related to its regular shape, but also influenced by eccentric inclusions with low conductivity inside the cell [111]. Currently, the use of a stationary electric field for cell rotation is still limited by the low precision of the speed control.

Alternatively, Han et al. [15] designed an ROT-based microchip to trap and rotate cells with an electric signal (Table 3 [15], [102], [105], [106], [7], [110], [111], [112], [113], [114]), in which the speed and direction of cell rotation was a sensitive function of the cell’s dielectric properties [36] (e.g., the conductivity and dielectric constant). Four electrodes were used to form a time-changing electric field required for cell rotation, and each electrode was energized by AC signals with different phase delays. It was also suggested [112] that there should be no more than four electrodes in real applications. Although the area of the rotating field expands as the number of electrodes increases (Fig. 4(d) [112]), the intensity of the central field remains the same and the control of multiple electrical signals becomes much more complex [115]. The only benefit of multiple electrodes is to minimize the effects of electric field distribution on cell rotation, as the uniformity of the electric field is improved.

Table 3. Summary of publications describing the development of cell rotation using electric field approaches.

Authors	Electric field type	Rotational DOF	Cell trap	Mechanisms	Manipulating tool	Rotating object	Applications
Han et al. [15]	Rotational	1	Yes	DEP; ROT	nQDEP; ROT signals	Human leukocytes and cancer cells	Measuring cellular dielectric properties
Benhal et al. [112]	Rotational	1	Yes	DEP; ROT	3–8 electrodes	—	Finite-element analysis
Walid et al. [110]	Stationary	1	No	DEP	AC electroosmotic flow	Barium titanate particles	Microfluidic device design
Huang et al. [114]	Rotational	1	Yes	ROT	nQDEP; ROT signals; shaped channels	HeLa cells	Microfluidic device design
Chen et al. [102]	Rotational	1	Yes	DEP; ROT	nQDEP; ROT signals	Pt–silica Janus particles	Analysis of the rotation direction
Zhao et al. [111]	Stationary	1	No	DEP	AC electroosmotic flow	Rat adipose stem cells	Analysis of the rotation under DEP
Huang et al. [7]	Rotational	3	Yes	DEP; ROT	nQDEP; ROT signals	Mammalian cells	Measuring cellular biophysical properties
Chow et al. [105], [106]	Rotational	1	Yes	3D DEP; ROT	Liquid metal electrode pipette	HeLa cells	Microfluidic device design
Huang et al. [113]	Rotational	1	No	ROT	Parallel and planar electrodes; polarized cells	HeLa and HepaRG cells	Polarized cells as electrodes

nQDEP: negative quadrupolar dielectrophoretic force.

In addition, it is recommended that cells not be rotated in the central electric field, as this may disrupt the electric field and could even terminate an experiment. To stabilize the rotational motion, Huang et al. [114] reported a new design of the DEP platform, which has the ability to trap single cells and achieve 3D rotation at the same time. By adjusting the AC signal configurations, cells can be rotated steadily, and the control process is much simplified. To further simplify such microdevices and extend the scope of applications, Huang et al. [7] presented a new ROT-on-a-chip technique (Fig. 4(b)). This method has advantages in performing 3D rotation in terms of controllable direction, speed, and axis of rotation on a single microchip with a typical structure, such as the structure described above. Based on the same design, Huang et al. [116] realized self-adaptive spatial localization control and the 3D morphology reconstruction of single cells. Compared with the multi-electrode design, Huang et al. [113] and Feng et al. [117] found that polarized cells can also work as electrodes; this novel ROT mechanism greatly simplified the design of DEP-based microchips (Fig. 4(e) [113]). Chow et al. [105], [106] fabricated a liquid metal-filled multifunctional micropipette for rotating cells in liquids (Fig. 4(a)); the micropipette can simultaneously generate a 3D DEP trap and a one-dimensional (1D) ROT. One unique advantage of this approach is that no microfabrication or lithography steps are required in order to form electrodes, which simplifies the fabrication process and reduces the fabrication cost.

In general, we can conclude that the applicable size range of electric field approaches (i.e., 0.001–1000 μm) is much wider than that of other approaches (see Section 4 later for a summary of the ranges). To date, most research has focused on cell rotation with only one DOF, rather than on cell rotation along multiple axes, which is still a challenge (Table 3); only Huang et al. [7] have successfully achieved cell rotation with three DOFs in an electric field with the aid of four electrodes.

3.2. Magnetic field approaches

Magnetic-field-based tweezers [118], [119], [120] are a reliable tool for studying the mechanical properties of biological micro-molecules, such as nucleic acidsand proteins comprising single molecules. A magnetic object placed in the magnetic field will experience a magnetic force and/or a magnetic torque, on the order of pico- to nano-newtons. Unlike electric tweezers, which are prone to cause undesired electrochemical reactions [121] and impair cell viability, the magnetic field has virtually no influence on biological samples. One of the limitations of this approach, however, is that biomolecules or cells of interest must be attached to magnetic particles for transportation, separation, and detection [122], [123], [124], [125]. Fig. 5(a) shows an example of a T cellattached to a magnetic Janus particle and rotated by an external magnetic field[13]. Given that the target cells require pretreatment, some research studies have shown that physiological characteristics may be changed as a result of attached magnetic beads [126], [127]. Another problem is that it is difficult to release the attached beads after the measurements of cell mechanical properties.

Magnetic tweezers (Fig. 5(b)) are formed when an external magnetic torque [89] is applied to magnetic microparticles. This technique is often used with OTs to trap target particles in specific places, as well as to overcome the limitations of OTs (i.e., photo-damage and thermal effects) on bio-sample manipulation. For example, Ye and Sitti [88] proposed the integration of both techniques to create a local vortex to transport nearby microorganisms along a circular path. However, Romodina et al. [122] reported that laser-induced local overheating will break down synchronous states between rotating particles and rotating magnetic fields, as the rotational motion will be delayed by the heat-related Brownian torque. In additional to optical trapping, fluidic trapping can be used in this case, and has been realized based on nickel nanowires [128], [129] (Fig. 5(c)) and a dumbbell-shaped magnetic actuator (Fig. 5(d) [130]). Both approaches have the ability to generate mobile micro-vortexes under a rotating magnetic field, in which cells can be trapped and rotated at a speed of up to 399.92 and 324.87 (°)·s−1, respectively.

Theoretically, in the magnetic field, TROT exerted on the magnetic dipole is defined as TROT = m × B, where m is the magnetic dipole moment of the particle and B is the external magnetic field. Under the influence of a magnetic torque, a magnetic particle will rotate until the direction of the dipole is aligned with the magnetic field. Thus, a time-variant magnetic field can cause a magnetic particle to rotate on a two-dimensional (2D) surface at a stable velocity. Thus far, numerous research studies have been done to measure the torque [131], [132] or forces [120] exerted on cells, DNA, and so forth under a time-variant magnetic field. However, as previously described, the Brownian motion may destroy the synchronization states, and the torque applied by the magnetic tweezers is not constant due to the difference in magnetization between magnetic beads [133], which makes it difficult to precisely quantify the magnetic force.

Similar to DEP-based rotation, most magnetic-based studies have realized a single degree of rotational freedom, rather than 3D control. In a study by Berndt et al. [134], the magnetic field was found to be capable of controlling the rotation of living specimens in a 3D space without any magnetic beads attached (Fig. 5(e)). However, this approach carries the risk of impairing the testing samples because of the excessive magnetic force applied for manipulation. In contrast, dumbbell fluidic tweezers (Fig. 5(d)) are a much safer way to achieve cell rotation, and a relatively fast rotation is achieved by non-contact manipulation (i.e., a mobile micro-vortex). However, the rotation speed of individual cells is unstable and varies with time. To date, precise cell manipulation for rotation or reorientation is still a daunting task for magnetic tweezers; thus, their use is still not recommended for both cases, except for larger model organisms that are commonly used in developmental biology, and which require high driving torques for actuation.

3.3. Acoustic field approaches

Acoustic-field-based tweezers can control objects in real time through the interactions of sound waves with solids, liquids, and gases, as first proposed by Wu [135] to capture and linearly translocate 270 μm latex particles and frog eggs. This technique can be applied for the manipulation of multiple bioparticles across a wide size range (0.1–1000 μm). The applications of acoustic tweezers can be roughly divided into three categories according to the working principles: ① standing-wave tweezers, ② traveling-wave tweezers, and ③ acoustic streaming tweezers. Among these, the first two groups are direct manipulation strategies with external acoustic radiation forces, while the last one is an indirect manipulation strategy induced by fluid flow.

3.3.1. Standing-wave tweezers

A standing wave is characterized by the ability to form a stable distribution of an acoustic potential energy field and a mechanical field. According to the generation method of an acoustic wave, standing waves can be further divided into two subtypes: surface acoustic waves (SAWs) and bulk acoustic waves (BAWs).

SAWs, which propagate along the surface of an elastic material, are typically generated on interdigital transducers (IDTs). Such transducers can convert electric signals to SAWs and generate periodically distributed mechanical forces. SAWs can move particles, cells, or microbes as precisely as OTs, and the particles in the acoustic field are pushed to either acoustic pressure nodes (i.e., minimum pressure regions) or pressure antinodes (i.e., maximum pressure regions), depending on the density and compressibility of the particles (Fig. 6(a) [136]). Moreover, this technique can manipulate particles independently of shape and can manipulate many particles in parallel; both types of manipulations are impossible for OTs [39]. Additionally, SAWs have potential for particle alignment. Bernard et al. [137] reported that non-spherical particles are prone to rotate and align with anisotropic potential wells. Furthermore, the applicable environment of SAWs is not limited to sticky conditions, such as in a droplet; for example, Yu et al. [138] reported that a SAW field with an annular-type pattern can be formed. In such droplets, as the distribution of the acoustic potential changes according to the acoustic amplitude, the internal particles exhibit different dynamic behaviors, such as rotation and translocation. Guo et al. [139] took advantage of this phenomenon to achieve the aggregation of a large number of beads, form specific shapes, and reorient the aggregated beads toward a signal input.

Compared with OTs and electric tweezers, which are typically used to manipulate single cells, acoustic tweezers are capable of rotating a large number of cells in parallel. Additionally, acoustic tweezers (e.g., 150 pN on particles smaller than 5 μm) have a larger output force on particles of the same size compared with magnetic tweezers (50 pN) or OTs (10 pN) [39]. It is worth noting that the applied wavelength of the acoustic waves must be comparable to the size of the particle in order to stably manipulate submicron particles.

BAWs are generated on a piezoelectric transducer and are typically used inside a microchannel. As shown in Fig. 6(b) [136], the reflected wave on the reflector interacts with the original wave, which produces pressure nodes and antinodes in the channel for multi-cell manipulation. Also, the number of these nodes can be changed by adjusting the voltage frequency relative to the geometric dimensions of the channel [140]. At present, this technique is commonly used for cell separation or focusing, and is rarely used for cell translation and rotation.

3.3.2. Traveling wave tweezers

As shown in Figs. 6(c) and (d) [136], traveling wave tweezers are mainly used for acoustic levitation. According to a review by Ozcelik et al. [136], they can be roughly divided into two groups, depending on the applied generator: namely, active methods and passive methods. The key difference is the number of transducers used; for the former, a relative phase delay between sound waves is generated by the sensor array and is used to form flexible pressure nodes; for the latter, only one transducer is sufficient to realize a complex acoustic field distribution and dynamic control of the particles.

More specifically, in 2015, Marzo et al. [141] identified several active methods and reported that particles could be suspended in mid-air and, by adjusting the phase delay between each transducer, particle rotation or translation was achievable and controllable by programs. In addition, for applications in fluids, Franklin et al. [142] proposed a simple and compact transducer that could generate stable 3D acoustic traps that helped particles to overcome gravity in fluids; these researchers realized translation manipulation. In the review by Andrade et al. [143], the acoustic suspension method is described as having the ability to hold objects in a fixed position and to rotate and translate objects in three dimensions.

In 2016, Melde et al. [144] proposed some passive methods, in which particles could be captured and transferred in acoustic holograms, but rotational manipulation could not be achieved. More recently, Muelas-Hurtado et al. [145]reported an effective approach to generate an acoustic Bessel vortex in air using a spiral active diffraction grating, which has the potential for precise manipulation. On the basis of this research, Li et al. [146] further analyzed the acoustic radiation torque of the first- and second-order acoustic Bessel vortex beams, and realized flexible rotation manipulation of objects of different shapes at a high speed. Due to the limited resolution, low controllability, and large transducer size, traveling wave tweezers are not yet available for the manipulation of micron-scale particles [147].

3.3.3. Acoustic streaming tweezers

Acoustic tweezers represent the fusion of acoustics and microfluidics, and can rotate cells or small organisms through the acoustic energy absorbed in liquids. As shown in Figs. 6(e) and (f) [136], controllable acoustic streams are normally formed around high-frequency oscillating microbubbles or microstructures. For example, an oscillating solid structure placed in a microfluidic environment can generate a local acoustic flow, as shown in Fig. 7(a), allowing the manipulation of nearby particles or cells that are trapped and rotated under an acoustic vortex flow. In addition, a high-frequency oscillation structure can be driven by external high-frequency acoustic waves. For example, Huang et al. [148]reported that by adjusting the input voltage applied to a piezoelectric transducer, the flow rate of the micro-vortex flow induced around the sharp edges in a microchannel is programmable (Fig. 6(f)). Thus far, the controllable rotation of cells around sharp edges has been realized by Ozcelik et al. [17] with a rotation speed that relates to the voltage signals and sharp-edged structures: An edge with a smaller angle or longer length can contribute to a higher rotation speed. Furthermore, Feng et al. [149] reported that an asymmetrical microstructure can contribute to 3D rotation manipulation in-plane or out-of-plane under a microscope. In their research, Feng et al. successfully kept the rotation speed of swine oocytes constant and used numerical simulation to study the rotation mechanism of the oocytes in acoustic streams. In addition to microstructures with sharp edges, microbubbles can function similarly to form local micro-vortexes in a microchannel; the functions and applications of oscillating microbubbles in microfluidic devices (Fig. 6(e)) have been summarized by Hashmi et al. [150]. It is worth noting that the force exerted on bio-samples depends on size, which means that larger microorganisms are susceptible to a larger rotational torque than smaller cells. Furthermore, it has been shown that the rotation rate of a cell varies as a squared function of the drive voltage [16]. Therefore, theoretically, the rotation speeds of cells or particles induced by acoustic streams may help to distinguish their sizes under the same excitation voltage. However, the acoustic parameters of microbubbles are unstable in the long run, since microbubble size and geometry are susceptible to change. Also, the spatial resolution of both structures (i.e., microbubbles and sharp edge structures) is low, which limits their practical applications.

3.4. Hydrodynamic field approaches

Hydrodynamic-field-based approaches can generate a micron-scale fluidic field in a variety of ways (Table 4 [19], [93], [17], [149], [150], [16], [151], [152], [153], [154], [155]), such as oscillating piezoelectric actuators (Figs. 6(e) and (f)), rotating magnetic microbeads in a rotating magnetic field [88], [122], [156], or controlling the flow rate within a micropipette [18], [19].

Table 4. Summary of publications describing the development of cell rotation using hydrodynamic-field-based approaches.