, , , , , , , , , , ,

Highlights

•
A comprehensive review of coupled radiation-free convection heat transfer is conducted.
•
Studies are categorized based on geometries with/without inner heated bodies.
•
General modelling procedures, governing equations, and parameters are outlined.
•
Significant results of various studies are summarized and highlighted.
•
Potential future directions are suggested.

Abstract

This paper represents a groundbreaking endeavor in consolidating the advancements achieved in the topic of coupled radiation-free convection (CRFC) across various investigated models. Through meticulous bibliometric analysis, the paper not only underscores the paramount importance of CRFC publications but also illuminates their frequency, signaling a burgeoning interest and significant contributions in this domain. The literature review is ingeniously structured, categorizing studies based on the types of cavities/enclosures with or without internal heating sources, thereby providing a comprehensive and structured overview of the field's landscape. It then delves into the crux of CRFC with an exposition of governing equations, assumptions, parameters, and variables, establishing a robust foundation. Transitioning seamlessly to application, the paper explores simulated models, boundary conditions, and insightful result discussions. Notably, the pervasive influence of surface thermal radiation in enhancing free convection heat transfer throughout the reviewed studies underscores CRFC's transformative potential, paving the path for innovative advancements in thermal engineering paradigms.

Keywords

Free convection

Heat transfer

Inner heated sources

Natural convection

Surface thermal radiation

Nomenclature

Abbreviations
CRFC	coupled radiation-free convection	t	time, s
Symbols	ΔT	temperature difference, K
Cp	specific heat, kJ/kg K	u, v	velocity components, m/s
d	size of an air cavity, m	X, Y	dimensionless coordinates
F_k-i	view factor from k-th element to the i-th element of an enclosure	U, V	dimensionless velocity components
G_r	Grashof number	Greek symbols
g	acceleration of gravity, m/s²	α	thermal diffusivity, m² /s
k	thermal conductivity, W/m K	β	coefficient of thermal expansion, 1/K
L	characteristic length	ε	emissivity
N_RC	radiation conduction interaction parameter	μ	dynamic viscosity of the fluid, Ns/m²
Nu_c	convection Nusselt number	υ	kinematic viscosity of fluid, m² /s
Nu_R	radiative Nusselt number	ρ	density, kg/m³
Nu_total	total Nusselt number	σ	Stefane-Boltzmann constant, W/m² K⁴
P	pressure, N/m²	ψ	stream function, m²/s
Pr	Prandtl number	ω	vorticity, 1/s
	radiative heat flux, W/m²	Ψ	dimensionless stream function
	incident radiative flux, W/m²	Ω	dimensionless vorticity
Ra	Rayleigh number	Θ	dimensionless temperature ratio
R_k	radiosity of the k-th element of an enclosure	τ	dimensionless time

1. Introduction

Recently, different techniques have been developed to enhance heat transfer in engineering systems [1], [2]. Natural convection is especially important for low-power and low-pressure thermal systems. Improving Natural convection heat transfer via surface thermal radiation is a critical aspect of thermal engineering, with wide-ranging applications in industrial, environmental, and technological domains [3], [4], [5]. The free convection phenomenon operates on the fundamental principle of fluid dynamics, where temperature differentials within a fluid create density gradients, leading to the formation of convection currents. As fluid is heated, it becomes less dense and rises, while cooler, denser fluid descends, establishing a continuous circulation pattern that facilitates the transfer of thermal energy from hotter regions to cooler regions within the fluid and this free convection is affected by several factors such as temperature difference, fluid properties, geometry, boundary conditions, porosity, etc. [6], [7], [8]. Simultaneously, surface thermal radiation complements natural convection by emitting electromagnetic waves from a surface due to its temperature. These waves, primarily in the infrared spectrum, carry thermal energy and can travel through a vacuum or transparent mediums. The intensity of thermal radiation emitted by a surface is determined by factors such as its temperature and emissivity, with higher temperatures and emissivities resulting in greater radiative heat transfer [9], [10].

The interconnection between radiation and natural convection is intricate and plays a pivotal role in heat transfer processes [9], [11], [12]. Temperature gradients generated by radiative heat transfer between surfaces can influence adjacent fluids, creating additional temperature differentials that drive natural convection currents in addition to radiative heat transfer. This interplay is particularly evident in environments where both mechanisms contribute significantly to thermal energy transport, such as in solar thermal systems, building HVAC systems, and industrial heat exchangers [13], [14].

One of the key advantages of natural convection heat transfer via surface thermal radiation is its efficiency [13], [14]. Natural convection harnesses fluid movement driven by temperature gradients, requiring minimal external energy input [15], [16]. This energy-efficient process is further enhanced by surface thermal radiation, which optimizes the distribution of thermal energy across surfaces, ensuring uniform heating or cooling [3], [17]. The adaptability of these mechanisms to various environments and applications makes them highly versatile and effective in addressing heat transfer challenges. Moreover, the environmental compatibility of natural convection heat transfer via surface thermal radiation aligns with sustainability goals [18], [19]. Furthermore, passive heating and cooling strategies utilizing these mechanisms reduce energy consumption and reliance on mechanical heating or cooling methods, contributing to energy-efficient building designs, eco-friendly heating solutions, and renewable energy applications [4], [20].

In practical applications, the connection between radiation and natural convection is often leveraged for optimized heat transfer and been widely considered for many applications, such as: electronic devices cooling [21], solar collectors[22], [23], micro-electromechanical system [24], closed cavity [25], heat exchangers [26], [27], [28], double windows [29], [30], etc. A variety of investigations have been accompanied to evaluate the characteristics of buoyancy-driven heat transfer for different geometries [31], [32], [33], [34]. Anciently, convection heat transfer was not affected by surface thermal radiation; however, it is significant [35], [36]. Currently, many researchers have interested in modelling the coupled radiation/natural convection (CRFC) systems.

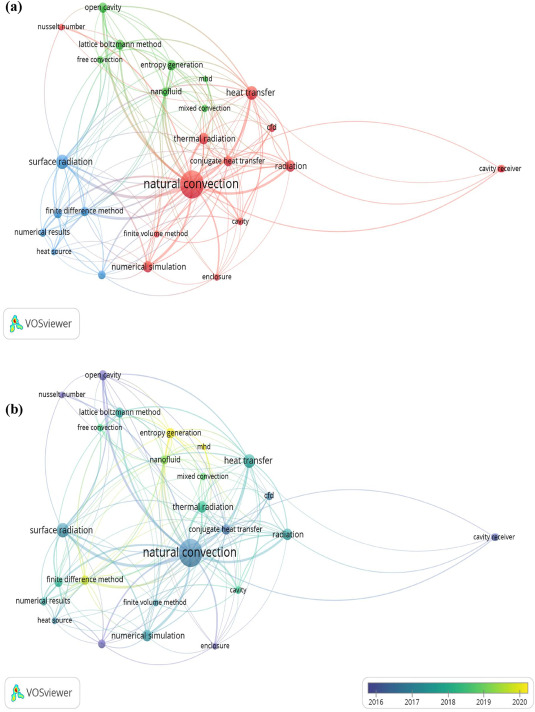
To show the importance of the investigated subject, a bibliometric analysis was conducted based on retrieved manuscripts from the Scopus database [37], [38]using the first three keywords of this article as the search queries. The collected database over of 19 years (2004 – 2023) includes all document types (i.e., review articles, research articles, conference articles, …) that contained the comprehensive metadata about each article. Beyond that, VOSviewer [39] was utilized to construct and visualize bibliometric networks. The hypothetical keywords’ network, illustrated in Fig. 1, shows the occurrence frequency of each keyword used by the authors (at least ten times). In this figure, each circle diameter represents the occurrence frequency of the keyword, connection line thickness refers to the times of using keywords together, and colors denote the (cluster (Fig. 1-a), and the average publication year (Fig. 1-b). It can be noticed that the most utilized keywords are "natural convection" and "surface radiation", especially in the period from 2016–2018. Additionally, the investigation of CRFC in cavities, mixed convection, Nanofluid, and the effect of thermal radiation are interesting topics from 2018–2019. Moreover, keywords such as "entropy generation" and "finite different method" are the most commonly used recently. Similarly, as shown in Fig. 2, the considered subject has been frequently and leadingly studied in China (107 documents), followed by India (78 documents) and the Russian Federation (77 documents), which had the highest number of citations in 1847 in the topic considered. Alternatively, despite having a low number of publications, the surveyed topic has been recently focused on by authors from some emerging nations, such as Saudi Arabia, Tunisia, Pakistan, and Vietnam. Further, being important, the current topic has been published and co-cited in highly impacted journals, as shown in the co-citation map shown in Fig. 3. In this figure, the journals are classified according to each cluster (color), similar to Fig. 1 (a), citation number (circle size), at least 10 citations/journal, 10 documents/journal, and the co-citation of the journal (line thickness). As shown, the investigated subject has been published, with high co-citation rate and more visibility in the following highly impacted journals: International Journal of Heat and Mass Transfer [5-Year Impact Factor: 4.662], International Journal of Thermal Sciences [5-Year Impact Factor: 3.893], Applied Thermal Engineering [5-Year Impact Factor: 6.465], Numerical Heat Transfer-Part A Applications [5-Year Impact Factor: 2.562 ], and International Communications in Heat and Mass Transfer [5-Year Impact Factor: 6.782]. Based on the conducted bibliometric analysis, the CRFC topic is an interesting and promising topic that has attracted the researchers' scope.

Overall, the complex interaction between natural convection heat transfer and surface thermal radiation highlights their importance in thermal engineering and heat transfer applications. Understanding and employing these mechanisms provide chances for improved energy efficiency, environmental sustainability, and technological advancement in various sectors. This work aims to offer a comprehensive and structured review of recent advancements in CRFC for various cavity/enclosure geometries, both with and without inner heated bodies. A key objective is to consolidate the efforts conducted on CRFC across various proposed models, categorizing the studies based on geometry types. Moreover, this review objectives to clarify the overall modelling processes, governing equations, and heat transfer parameters that are relevant to CRFC systems. Furthermore, the paper emphasizes the impact of surface thermal radiation on enhancing free convection heat transfer through the analysis of representative studies, presentation of model specifics, boundary conditions, and major results. Finally, this study identifies potential areas for further research and suggests future paths, such as exploring intricate geometries, studying the impact of turbulence, and analyzing advanced materials.

2. Classification of various research scenarios from the literature

2.1. Coupled radiation-free convection in cavities/enclosures without inner heated bodies

The principle of CRFC, particularly in closed cavities, has been extensively investigated and categorized into two cases: with radiations wall only, and with gas and radiations wall. The latter, which is essential in combustion systems, has been regarded in many works, as reported in [40], [41], [42], [43]. However, this case is not presented in the current survey; only the former category is focused.

Many earlier investigations have been conducted for differentially heated rectangular enclosures [44], [45], [46], [47], [48]. According to the reported numerical studies of CRFC by Balaji and Venkateshan [49], radiation revealed a dual influence: reducing the convective component and participating in the overall heat transfer. However, more complex formulae for calculating radiation were still required as simple ones were insufficient. Hence, correlations for CRFC, regarding air as a working medium, were proposed by Balaji and Venkateshan [50]. According to an experimental investigation by Ramesh and Venkateshan [35], the previous correlations were adequate and valid. Ridouane et al. [51] numerically evaluated the CRFC for a 2D square cavity enclosure having a heated base with four emissivity combinations at which isothermal horizontal walls differed from the adiabatic vertical ones and set at (ε =0.05 or 0.85). As a result, compared to pure free convection, the surface radiation influenced the steady-state modes' ranges and periodic solutions' nature and magnitude. On the other hand, for the rectangular cavity, Gad and Balaji [52]determined the Ra (Rayleigh number) for the convection onset in terms of adiabatic sidewalls' emissivity and aspect ratio. For this model, the upper horizontal wall was set at 303 K, the emissivity of the horizontal wall was constant (ε = 0.85), and the aspect ratio ranged from 1 to 10. According to their results, surface radiation influence diminishes beyond the aspect ratio of 5, and high emissivity of sidewalls delayed the Rayleigh-Benard convection onset. Inversely, for a top-heated open-ended cavity, Manca and Nardini [53]experimentally evaluated the CRFC utilizing high emissive horizontal walls (ε = 0.8). As concluded, the unheated bottom wall witnessed a temperature rise that could cause secondary motions in different observations to low emissive walls [54]. These secondary motions occurred by plumes within the cavity adjacent to the bottom plate at (Ra = 1.92×10⁵), based on flow visualization at transversal sections. Also, due to surface radiation, secondary convection was obtained near the sidewalls of industrial buildings that enhanced air flow and temperature patterns [55]. Moreover, the surface radiation significantly modified both flow and temperature patterns affecting the heat transfer process within a square enclosure as reported by Akiyama and Chong [56] and Lari K et al. [57].

2.2. Coupled radiation/free convection in cavities/enclosures with inner heated bodies/sources

The presence of an inner heated body significantly alters the flow dynamics compared to scenarios without such a body [58]. Without an inner heated body, convection currents primarily form around external surfaces, driven by temperature differences between these surfaces and the surrounding fluid. In contrast, when an inner heated body is present, it introduces additional heat sources within the fluid volume, leading to more complex flow patterns. This internal heating creates localized temperature gradients, which can induce buoyancy-driven flows within the fluid bulk. As a result, the combination of external surface convection and internal heating from the heated body enhances overall heat transfer rates but also introduces challenges in predicting and controlling fluid flow patterns [59], [60].

Various studies on CRFC for cavities/enclosures having inner heated bodies have been done [61], [62], [63], [64]. Mezrhab et al. [65], and Mezrhab and Bouali [66] evaluated the CRFC of a square cavity, including a heated cylinder. In addition, through a centered square body, a differentially heated square cavity was investigated by Mezrhab et al. [67]. As reported, when considering radiation, the heat transfer and flow pattern were highly augmented compared to the enclosure without an inner body. In addition, the CRFC was analyzed by Saravanan and Sivaraj [68], considering a square enclosure containing a discrete square heater with cooled and insulated vertical and horizontal walls, respectively. Also, discrete heaters inside a square enclosure were proposed by Saravanan and Raja [69]. On the other hand, a horizontal annular cavity surrounded by an inner heated elliptic cylinder was analyzed by El Moutaouakil et al. [70] exploring the CRFC. Moreover, Nguyen et al.[64] investigated CRFC in a cubic chamber containing a mixture of air and water when a heated obstacle is present. Also, Hidki et al. [71] studied numerically the influence of 2 heat-generating bodies based on CRFC in air cavities. Furthermore, El Moutaouakil et al. [72] examined the influence of a partially heated cylinder on CRFC heat transfer. Finally, Moussaoui et al.[73] applied the concept of CRFC in a square cavity with a heated bottom. For this work, the 2D analytical method was utilized. All works proved the obtained augmentation in heat transfer when thermal radiation was considered.

2.3. Coupled radiation/free convection in vertical parallel plate channels

The investigated CRFC with vertical parallel plates has been examined for a long time. For laminar free convection, using asymmetric heating, Carpenter et al. [74] evaluated the CRFC for vertical parallel plate channels via employing numerical parabolic formulation and Boussinesq approximation. The investigation was conducted to estimate the impact of dimensionless variables, namely: Ra number, heat flux ratio, radiation number, emissivity, and aspect ratio. The results displayed surface radiation's ability to change the wall temperatures, particularly the peak value. Also, for laminar convection, Krishnan et al. [75]experimented CRFC for parallel plates: two unheated (ε = 0.05), and one high emissive central plate (ε = 0.85). This work is considered as a proof of the successful impact of radiation at room temperature. In addition, surface radiation was proved to be feasible in the case of asymmetric heating more than symmetric heating, according to experimental work by Manca and Naso [76]. At high emissivity, flow patterns approached those of symmetric heating and Rayleigh number was reduced. Additionally, Lakhi and Safavinejad [77] tested CRFC numerically between two parallel plates (various angles). They showed that radiation factors significantly affect heat transfer (both airspeed and temperature profiles of the fluid) between them. Moreover, increasing the angle between the plates and the horizontal increase also air speed, temperatures, and buoyancy effect.

3. General modeling procedures and governing equations

Modeling natural convection heat transfer via surface thermal radiation involves a systematic approach that considers fluid dynamics, thermal radiation, and heat transfer principles. The governing equations governing these phenomena are fundamental in developing accurate models. Here are the general modeling procedures and governing equations for natural convection heat transfer via surface thermal radiation:

Fig. 4 shows the general procedures that should be followed while modelling the CRFC. For Step 1, the model schematic differs according to the configuration (e.g. rectangular, square, trapezoid, cylindrical...etc.), and the location of the heated wall/body (e.g. top-heated, bottom-heated, local heater, heated body…etc.). Based on the proposed configuration and study aims, step 2 can be done. Generally, for free convection, many assumptions are considered [31]. However, for the CRFC case, the following are selected:

•[78]
•[79]
•[80]
•[78]
•[81]
•[82]

Step 3's governing equations are derived based on the considered model configuration.

However, generally, in the case of cartesian coordinates in 2D (x,y), the continuity [83], [84], momentum, energy equation, and stream function equations can be summarized as follows [19], [59]:(1)

(2)

Momentum in (y-direction, let temp. variation in this direction):(3)

(4)

Stream - vorticity function:(5a)

(5b)

Step 4

dimensionless parameters (dimensionless coordinates (X, Y), dimensionless velocity components (U, V), dimensionless stream function (Ψ), dimensionless vorticity (Ω), dimensionless temperature ratio (Θ), and dimensionless time (τ)): the two approaches can be taken into consideration when dimensionless parameters are formed:

•
1^st approach:

and stream-vorticity function is [85, 86]:

•
2^nd approach:

and stream-vorticity function is:

Additionally, the following dimensionless numbers are used to evaluate the CRFC model:

The radiative heat flux can be calculated using different approaches, as follows:

i

,

as reported by [87].
ii

as reported by [88].
iii[45]

4. Results and discussions of several explored geometries, encompassing various models, and boundary conditions

This section presents different proposed geometries and corresponding boundary conditions with the associated results. Herein, the main focus is on the effect of ε on the heat transfer characteristics, especially N_u.

4.1. Cavities/enclosures without inner heated bodies and vertical parallel plate channels

Gad and Balaji [52] investigated the influenced onset of convection for a Rayleigh– Benard configuration (Fig. 5(a)) by thermal radiation. Four different values of ε (range = 0 to 0.85), and variable aspect ratios (ARs) were proposed. According to the result, the effect of radiation decreased with the increase of AR till (AR=8) and then vanished as shown in Fig. 5(b). For AR=1, Fig. 5(c) and (d), except for 1×10⁴< Ra<5×10⁴, the convective components varied inversely with ε. But, generally, the surface radiation enhances the heat transfers across the cavity. There are three kinds of regimes have occurred: (i) for 4×10³< Ra<1×10⁴, there was no effect on convection due to emissivity, (ii) for 1×10⁴< Ra<5×10⁴, the flow structure turned from unicellular to bicellular for higher emissivity, i.e., increase in convection, and (iii) beyond 5×10⁴, the convection suppression occurred with the emissivity increase. For AR=2, Fig. 5(e) and (f), just the bicellular structure appeared with the validity AR=1, i.e., convention enhancement and radiation declined with emissivity. For AR=3, both tetra-cellular and tri-cellular flow structures occurred when radiation was regarded for the proposed range of Ra. Then, with the increase of AR, the convection declined.

Wang et al. [3] proved the significant effect of thermal radiation on convection for a proposed cavity having a porous medium, as shown in Fig. 6(a). Due to surface radiation, the temperature field was changed for both free and porous regions. As R_a increased, temperature gradients were formed on a porous medium at two upper corners with a decrease in mean temperature at the interface. Regarding Fig. 6(b) and (c), which illustrate the variation of Nu_c with ε at Ra = 10⁴ and 10⁶, respectively, Nu_c at the free flow region was significantly affected by ε more than that of a porous region with greater change because the lack of radiation and the weakness of convection within the porous region. In addition, with the rise of ε, the presence of thermal radiation led to a growing temperature gradient adjacent to the hot wall, hence, Nu_c increased. However, with a further increase in ε, Nu_c at the hot wall became lower than at the cold one, and a slight increase in temperature gradient appeared near the cold side. This is attributed to the proportionality of radiative energy with T⁴, which augmented the heat transfer from the hot side to the adiabatic top side compared to the cold side. Whereas the radiative energy weakened the gradient adjacent to the hot side and inversely at the cold one. For Nu_R, Fig. 6(d), a direct increase with ε was obtained as expected. All these findings assure that surface thermal radiation had a good influence on convection heat transfer.

Bousetta et al. [89] conducted a numerical study on CRFC between vertical plates under asymmetric heating. The model shown in Fig. 7 (a) was proposed and the range of emissivity (0.1 – 1) was considered. As illustrated in Fig. 7 (b), Nu_c was slightly modified at (ε=0.1) and reduced at (ε=1). For Nu_R, the same order of Nu_c was obtained; however, Nu_R increased with ε. Both Nu_c and Nu_Rincreased with Ra at the same value of ε. Moreover, the CRFC resulted in declination in maximum T_H, reaching a reduction of 24.4K. It was also reported that there were increased deviations between inlet and max. wall temperatures up to ∼200K had a negligible effect on the heat transfer process.

Said et al. [90] numerically evaluated the CRFC for the annular air gap of two concentric cylinders, illustrated in Fig. 8(a). The governing equations were derived in (r, θ) coordinates. The calculations were conducted at ranges of Ra (10³ to 10⁶) and ε (0 to 1); whereas the curvature ratio was constant at 2. The results revealed that Nu_c varied within the proposed ranges as it increased before (Ra≥10⁵) and (ε≥0.3), then decreased, as noticed in Fig. 8(b). But for Nu_R, Fig. 8(c), it was constant within the Ra range and increased with ε. The total Nu increased with both Ra and ε. Hence, it can be confirmed that radiation successfully affected the heat transfer process.

4.2. Cavities/enclosures with inner heated bodies/sources

Boukendil et al. [91] numerically simulated CRFC of asymmetrically cooled (single vertical wall at T_C=293K) enclosure having discretely heated body (circular cylinder at 297K<T_H<357K), Fig. 9(a), whereas the other remaining parts were insulated. The heat transfer process was evaluated at (10³<Ra<10⁷) and (0<ε<1). The results showed that both Nu_c and Nu_total increased monotonically with Ra with high growth at high Ra, as shown in Fig. 9(b). The value of Nu_R (Nu_total - Nu_c) also increased significantly at high Ra. As obviously shown, Nu_c was independent of ε. It was also concluded that surface radiation contributed by half of overall heat transfer.

Miroshnichenko and Sheremet [92] conducted a numerical evaluation of natural convection in the presence of thermal radiation for a tilted square cavity having a local heater, as illustrated in Fig. 10(a). The governing Equations (1-5) were modified by the addition of turbulent parameters (e.g., ν_t) and k-ε was considered as reported by [93], [94], [95]. The study was conducted at (0<φ<2 π), (10⁸<Ra<10¹⁰), and (0<ε<0.9). The higher the tilt angle the lower Nu_R was obtained, and the maximum heat transfer occurred at φ = 5π/6. Moreover, at π/3<φ<5π/6, the value of Nu_c was enhanced by 51%. In addition, the surface radiation enhanced the flow pattern. Furthermore, for constant values of Ra and φ, the Nu_total was enhanced with the increase of ε and τ, as shown in Fig. 10(b) and Table 1, however, the Nu_c was slightly enhanced. Finally, Finally, Table 2compares these studies with the ones mentioned in the previous literature regarding the Nusselt number obtained, emissivity range, Rayleigh number range, and the type of geometry studied.

Table 1

Emissivity (ε)	Nu_R	Nu_c	Nu_total	Enhance in heat transfer (%)
0	0	78.4	78.4	0
0.3	22.3	80.4	102.7	31
0.6	46.4	81.7	128.1	63
0.9	72.6	82.6	155.2	98

Table 2

Geometry	Emissivity (ε)	Highest total Nusselt number (Nu)	Rayleigh number (Ra)	Ref
Rayleigh– Benard configuration	0-0.85	10	1×10⁴< Ra<5×10⁴	[52]
Rectangular cavity with horizontal porous layer	0-1	18.7	Ra =10⁴ and Ra =10⁶	[3]
Asymmetrically heated vertical channels	0.1-1	42	10² < Ra< 10⁸	[89]
Vertical cylinder partially annular	0-1	33	10³ < Ra< 10⁶	[90]
Rectangular cavity with a discretely heated inner body	1	27.5	10³<Ra<10⁷	[91]
Inclined rectangular cavity with local heater	0-0.9	155.2	10⁸<Ra<10¹⁰	[92]
2D square cavity enclosure having heated base	0.05 or 0.85	16.6	10³<Ra<2.3×10⁶	[51]
A cavity having a square body at its center	1	65	10³<Ra<10⁸	[67]
An air‐filled square cavity containing two heat‐generating bodies	0-1	45	10³ < Ra< 10⁶	[71]
A square cavity partially heated cylinder	0-1	21	10³<Ra<10⁷	[72]

5. Conclusions

The paper reviews recent advancements in CRFC heat transfer across different geometries and heating configurations. It highlights the significant role of surface thermal radiation in enhancing free convection heat transfer. The key findings that can be summarized from the explored studies show that the influence of radiation could decrease with the growth of the aspect ratio of rectangular cavities without inner heating bodies and may vanish at high ratios. For vertical plates under asymmetric heating, large differences between inlet and max. wall temperature had a negligible effect on the heat transfer process. Besides, the value of Nu_c may monotonically vary with ε; however, the total Nu can be enhanced due to the increase of Nu_R; hence, the thermal radiation successfully augments the heat transfer process. Furthermore, surface radiation can contribute to half of the overall heat transfer.

Finally, many future research directions can be suggested. One is to investigate other complex geometries with and without various heated objects with different orientations. The second is to model natural convection using 3-dimensional analysis, considering the effects of turbulence and compressibility. The third is to examine the use of advanced materials with tailored thermal properties to enhance surface thermal radiation effects and improve overall heat transfer efficiencies in natural convection systems.

Ali Basem: Writing – review & editing, Methodology, Formal analysis. Wissam H. Alawee: Writing – review & editing, Investigation, Formal analysis. Meng An: Writing – review & editing, Visualization, Validation, Conceptualization. Swellam Wafa Sharshir: Writing – review & editing, Writing – original draft, Visualization, Validation, Formal analysis, Conceptualization. A. S. Abdullah: Writing – review & editing, Methodology, Formal analysis. Sung-Hwan Jang: Writing – review & editing, Writing – original draft, Methodology, Investigation, Conceptualization. M. Ismail: Writing – review & editing, Writing – original draft, Visualization, Validation, Investigation, Conceptualization. Mamoun M. Elsayad: Writing – review & editing, Writing – original draft, Validation, Investigation, Data curation. A. W. Kandeal: Writing – review & editing, Writing – original draft, Visualization, Validation, Data curation, Conceptualization. Hasan Sh. Majdi: Writing – review & editing, Visualization, Investigation, Conceptualization

Uncited reference

[85]; [86]; [88].

Declaration of Competing Competing Interest

The authors confirm that there is no conflict of interest to declare.

Acknowledgment

The authors extend their appreciation to Prince Sattam bin Abdulaziz University for funding this research work through the project number (PSAU/2024/R/1445). Also, this work is supported by the Research Grant funded by the Hanyang University ERICA. Ansan, Gyeonggi-do, 15588, South Korea

Data availability

No data was used for the research described in the article.