Dynamics of prey predator with Holling interactions and stochastic influences

1. Introduction

The mathematical modeling plays a central role in studying ecological interactions. Mathematical models, though important, play a subsidiary role to experimental research. Ecology, however, is different; experiments are often difficult to perform. For this reason, the predictions of mathematical models in ecology have, in many cases, to be relied on without detailed experimental corroboration. Different kinds of prey–predator interactions have been studied extensively by researchers after it was modeled and studied by Lotka [1] and Volterra [2]. Eminent mathematicians and ecologists contributed to the growth of this area of knowledge, and has been extensively reported in the treatises of Meyer [3], Cushing [4], Colinvaux [5], Freedman [6], Simmons [7] and Kapur [8]. Delayed diffusive autotroph herbivore population ecosystem with nutrient recycling studied by Gazi [17] prey predator system with prey population is infected by micro parasite and its stability analysis studied by Mukherjee [9], [10], [16]. The influence of both prey and predator density on kill rates in the system of large mammals, wolves and moose, directly observed by Peterson [13]. Xiao and Chen [11], [12] analyzed the prey predator model with disease in prey. The positive equilibrium is asymptotically stable for some parameter values but for other parameter values the equilibrium points are unstable. A prey predator model both the species are subjected to parasitism is developed and analyzed and an epidemic threshold theorem is proved by Hadler and Freedman [6], [18].

Predation is a straightforward inter species population interaction. One species uses other as a food resource (“Probably the commonest death for many animals is to be eaten by something else” - Charles Elton, 1927). Theoretically, the predator can destroy all the prey so that the prey become extinct. However, if it happens the predator will also become extinct. Predator depends on the prey for its existence and predators play an important role in controlling prey population strength in many systems. Very often, but not always an increase in prey density results in a straightforward increase in predator population size. The action of the predator in the face of increasing prey availability can take different forms, such as linear, curvilinear fashion. In real situations the relation between prey and predator is dynamic in nature, because they are influenced by climate dynamics, changes in food availability for prey species and dynamics in other areas of food web.

Consider the populations of two interacting species with population sizes x1(t) and x2(t) respectively modeled by a system of two first order differential equations. $x_{1}^{'} (t) = F (x_{1}, x_{2})$ $x_{2}^{'} (t) = G (x_{1}, x_{2})$

Different kinds of biological interactions between the species are characterized by $F (x_{1}, x_{2})$ and $G (x_{1}, x_{2})$ which are equal to the growth rates of the $x_{1} (t)$ and $x_{2} (t)$ . One kind of interaction that occurs in most common in nature is prey predation. In prey predation interaction, one species is the food for the other. One species is known as prey is flourishing with the interaction of the other species known as predator; prey is a food for the predator. This situation is modeled mathematically by Lotka-Volterra as $x_{1}^{'} (t) = x_{1} (λ - {ax}_{2})$ $x_{2}^{'} (t) = x_{2} (- μ + β x_{1})$

This mathematical model is unrealistic to support many prey predator systems, because this is much influenced by the initial conditions and by the perturbations around the equilibrium points. The more realistic model by the assumption that in the absence of predators, prey species obeys the logistic growth law, leads to $x_{1}^{'} (t) = x_{1} (λ - {ax}_{1} - {bx}_{2})$ $x_{2}^{'} (t) = x_{2} (- μ + {cx}_{1})$

The more realistic model due to Rosenzweig-Macarthur is given by $x_{1}^{'} (t) = x_{1} f (x_{1}) - x_{1} x_{2} ϕ (x_{1})$ $x_{2}^{'} (t) = x_{2} ({cx}_{1} ϕ (x_{1}) - g (x_{2}))$

In the absence of predator x2 this model would reduce to $x_{1}^{'} (t) = x_{1} f (x_{1})$ . Thus, $x_{1} f (x_{1})$ represents growth rate of the prey species by itself. In the absence of prey x1 this model is reduced to $x_{2}^{'} (t) = - x_{2} g (x_{2})$ . The term $x_{1} x_{2} ϕ (x_{1})$ is called the predator functional response and $x_{1} ϕ (x_{1})$ is the number of prey consumed per predator in unit time. The constant c is the conversion efficiency of prey into predator food and the term ${cx}_{1} x_{2} ϕ (x_{1})$ is called predator numerical response. It is reasonable to assume $ϕ (x_{1}) ⩾ 0$ and $ϕ^{'} (x_{1}) ⩽ 0$ , ${(x_{1} ϕ (x_{1}))}^{'} ⩾ 0$ and also $x_{1} ϕ (x_{1})$ is bounded as $x_{1}$ tends to infinity. Choice of Predator functional responses influences the qualitative predictions of mathematical model. Plankton-eukaryotic dynamics are delicate to the choice of the predator’s functional responses. Holling type III functional response merely explains the dynamics of plankton.

Type III functional responses can arise in the fallowing situations

(a)
The predator is moved to spend more time for hunting the prey species when prey species are more plentiful, perhaps in response to increased prey odor or metabolites [19], [20].
(b)
The prey occur in patches of different densities and predators choose the patches having more densities for predation.
(c)
The experiments conducted by Landenberger [21] who showed that, starfish feeding on turban snail in laboratory. Each predator was kept as a fixed density of prey. The number of prey eaten was recorded every day over a period of 90 days. The predator started out with type III response. Recent studies are showing results that ocean acidification affects predator prey response. Acidification of ocean makes harder for sea snails to hide from their sea star predators.

These assumptions express the idea that as prey population increases the consumption rate of prey per predator is increased but the fraction of the total prey population consumed per predator decreases. Sometimes the prey predator eco system is influenced by growth of civilization. It influences the rate of interaction between the prey and predator, to consider this fluctuation, the model should be more realistic in nature by incorporating the randomness (random fluctuations) in the model equations. The basic assumption is the randomness that is also proportional to the size of the population.

2. Mathematical model

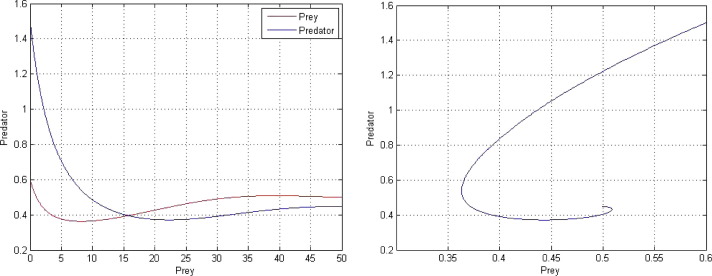
In the present model a prey predator system in which the predator has to consume more of prey to have an increase in the size of the predator that is the rate of decrease in prey is more than the rate of increase in the predator. Also the response of the interaction of the prey with predator follows Holling type III. It is assumed that there is no food source for predator other than the prey. Also both prey and predator follow logistic growth law (see Fig. 1, Fig. 2, Fig. 3).