Lagrangian generic second order traffic flow models for node

1. Introduction

Traffic flow models have been developed for many purposes such as traffic operations, management, control, evaluation, planning, prediction, congestion monitoring, and safety. For most of these applications, macroscopic models are well suited, as they are simple and robust with modest requirements in terms of data processing and analysis, low computational cost and precision as well as identification and calculation. This study revolves road network modeling applying macroscopic traffic flow models. First order traffic flow models have been used for quite a long time for modeling traffic flows on networks (Garavello and Piccoli, 2006, Lebacque and Khoshyaran, 2002, Zhang et al., 2009). In particular, the seminal LWR model has been widely used (Lighthill and Whitham, 1955, Richards, 1956). The LWR model is simple, and still takes various elements into consideration, for instance, capacity, storage, fundamental diagram, and traffic phase. However, first order models are not able to accurately recapture specific traffic flow phenomena such as the capacity drop, the bounded acceleration of vehicles or the stop- and go-waves, without being specifically adapted. They implicitly assume instantaneous speed change (Zhang, 2000). It can easily be extended in order to accommodate individual behavioral attributes that may be needed for assignment, for communication, and information and for traffic management methods involving V2X (including vehicle-to-vehicle (V2V) and vehicle-to-infrastructure (V2I) communications, i.e., the generic second order models (GSOM). The GSOM family encompasses a large variety of higher order traffic flow models, such as the LWR standard model which is basically a GSOM model with no specific driver attribute, the LWR model with bounded acceleration (Lebacque, 2002, Lebacque, 2003), the ARZ model standing for the multi-commodity models (Aw and Rascle, 2000, Jin and Zhang, 2004, Khoshyaran and Lebacque, 2008, Zhang, 2002), and the 1-phase Colombo model deduced from the 2-phase Colombo model (Colombo, 2002, Lebacque et al., 2007).

The present study focuses on the GSOM family. Authors developed an efficient numerical method to be applied to GSOM family. It includes methods to simulate traffic flow over nodes, which are required elements to simulate networks traffic, including inflows, outflows, and nodes at which roads merge or diverge or road properties change. Therefore, the next step in the development of the traffic flow model and accompanying numerical method is the introduction of nodes. GSOM models have been already well studied on homogeneous roads but little attention has been drawn to their implementation on nodes (as it is discussed in Section Methodology for the Lagrangian modeling of nodes). However, nodes (geometry, phases, traffic light operations, etc) are the main source of congestion for traffic streams on a network. Thus, the GSOM model (Section GSOM family) can be further developed. Consequently, the numerical method can be further improved (Section Lagrangian discretization of the GSOM family). The node model in Lagrangian coordinates deserves a special attention (Section Methodology for the Lagrangian modeling of nodes). In this paper, authors will discuss how to deal with inflow and outflow boundaries and inhomogeneity. Inhomogeneity is, for instance, changes in the fundamental relations due to changes in the number of lanes or speed limit, off ramps (diverges) and on ramps (merges). In the authors' model links are homogenous road stretches connected by nodes. Boundaries and inhomogeneity are located at the nodes. Therefore, authors refer to models for inflow and outflow boundaries, inhomogeneity, merges, and diverges as node models.

High-order macroscopic traffic models concerning nodes (intersections and geometry changes) are fundamental studies. Over the past years, many node models have been proposed, such as point-wise and non point-wise. Integration of node modeling seems to be a promising research area for some aspects of transportation planning, improving the quality of identification and calibration, extensive and sophisticated networks modeling, understanding of the capacity drop (hysteresis), traffic management and control applications (such as ramp metering, speed control, reactive and dynamic allocation, etc) (Bhouri et al., 2016, Buisson et al., 1996, Jin and Zhang, 2003, Lebacque, 1996, Lebacque, 2003, Lebacque and Khoshyaran, 2001, Lebacque and Khoshyaran, 2005). Hence, node modeling is therefore crucial for the simulation tool and the accuracy of the developed model. Still, this is a difficult, complex and delicate process. Vehicles and drivers already have plans (specific origin and destination) and therefore precise itineraries, which made node modelization difficult.

The traditional numerical methods are generally easier to extend with these node models, but also node models based on the Lagrangian coordinate system can be implemented and lead to satisfying results. The main challenge of node modeling in Lagrangian formulation is that nodes move with respect to the coordinate system, which moves with the vehicles. Therefore, one may develop node models similar to the ones that are used in microscopic models. However, the continuous link model describes the average vehicle behavior. Therefore, the node model and its discretization should also describe the average vehicle behavior and thus authors did not resort to microscopic node models depicting the behavior of individual vehicles. Authors consider macroscopic node models and introduce node models in Lagrangian formulation in analogy to those in Eulerian formulation. Thus, the aim of this paper is to develop a new node model based on non point-wise by expressing upstream and downstream boundary conditions into Lagrangian coordinates. The model takes into account internal node dynamics as well as physical properties of nodes (storage capacity, maximum through-flow, traffic supply and demand). The reason of introducing this internal node dynamics (or this buffer) between upstream and downstream links is detailed in Section Difficulty in dealing with a node model. The node model is therefore extendable to the GSOM model family. The developed node model is based on Lagrangian GSOM model which is compatible with microscopic and macroscopic descriptions. The microscopic representation of traffic flow is particularly suited for traffic management methods, while staying compatible with a macroscopic representation allowing global evaluation. The overarching objective of conciliating both microscopic and macroscopic representations is to recast the macroscopic model under its Lagrangian coordinates. Indeed the Lagrangian framework focuses directly on the vehicles and incidentally it allows to keep track of individual behaviors (Leclercq et al., 2007).

Furthermore, many parts of the world traffic are generally organized, flowing in lanes of travel, with interchanges, traffic signals at nodes to facilitate the orderly and timely flow of traffic. Traffic management aims at improving traffic services by the microscopic or macroscopic and dynamic processes on analysis. For this purpose an application of traffic control at nodes using traffic light signals is provided in this study for solving the proposed traffic flow model.

The purpose of this work is to develop a realistic network model which is compatible with both microscopic and macroscopic descriptions, and satisfy classical constraints coming from the engineering world, for instance, the invariance principle, as discussed in previous researches (Lebacque and Costeseque, 2014, Lebacque and Khoshyaran, 2005, Tampère et al., 2011). Therefore, authors add discretization of node models that depict inflow and outflow boundaries (in order to perform simulations on networks of roads).

The invariance principle is used to study the asymptotic behavior of solutions of differential equations. This principle implies that traffic flow over the node heavily depends on the flows over the incoming links. Lebacque and Khoshyaran (2005) have shown that this is an unreasonable assumption. As an example, consider the case with low flows (in total below the capacity of the outgoing link) from both incoming links. If the flow from one incoming link is halved, the flow from the other incoming link to the outgoing link is also halved.

Indeed, an intersection model for node (z) connects the outflow boundary conditions of the upstream links (i) and the inflow boundary conditions of the downstream links (j). Note that the node model is defined as a function F which associates to the vectors of node boundary conditions (demand δ and supply σ) and the vector of node through flows (outflow q and inflow p): (q, p) = Fz (δ, σ).

The invariance principle expresses that the node model is compatible with the Riemann half-problems on the links (i) and (j). It can be expressed as follows Fz(δ, σ) = L (Fz (δ, σ); δ, σ).

The interested reader could also refer to Lebacque and Costeseque, 2014, Lebacque and Khoshyaran, 2005, Tampère et al., 2011 for more details on this principle.

The paper is organized as follows. In Section GSOM family, the GSOM family is introduced. Section Lagrangian discretization of the GSOM family is dedicated to the description of the numerical resolution of the GSOM model using the Lagrangian discretization method. The complete numerical methodology on node and the description of the internal state node model are depicted in Section Methodology for the Lagrangian modeling of nodes. A numerical example illustrating the impact of traffic lights on the node model is shown in Section Simulation results. In section Conclusions, authors provide some conclusions on this work and give some insights on future research.

2. GSOM family

2.1. Structure of the GSOM model

The GSOM model combines the conservation equation with the fundamental diagram of specific driver behavior attribute. The main GSOM traffic model variables on a road network are the density $(ρ)$ expressed in veh/km, the flow $(q)$ expressed in veh/h, the speed $(v)$ expressed in km/h, the driver attribute $(I)$ , which characterizes the behavior of each driver and can be the type of vehicle, the origin/destination, the driver aggressiveness, the driver destination or the vehicle class, etc, the position $(x)$ , and the time $(t)$ . The speed is a function of the density $(ρ)$ and the attribute $(I)$ (the speed-density fundamental diagram).

It can be expressed as follows.(1) ${\begin{array}{l} \partial_{t} ρ + \partial_{x} (ρ v) = 0 & Conservation of vehicles \\ \partial_{t} (ρ I) + \partial_{x} (ρ I v) = ρ f (I) & Conservation of the driver attribute I \\ v = ℑ (ρ, I) & Speed - density fundamental diagram \end{array}$ where the function f(I) is a relaxation function. It is preserved along the trajectories of vehicles. The fundamental diagram is $v = ℑ (ρ, I)$ and $ρ v^{\underline{\underline{def}}} R (ρ, I)$ . $ℑ$ is the speed-density fundamental diagram. R is the flow-density fundamental diagram and it is assumed to be concave with respect to (ρ), for all values $I : R (p, I) \mapsto p ℑ (p, I)$ .

Note that the equation of $I$ can be reformulated as an advection equation $\dot{I} = \partial I / \partial t + v (\partial I / \partial x) = f (I)$ . In this context, the function f(I) can express the relaxation of I to a reference or an equilibrium value (specific to the driver), or can express a disturbance process, in the case of the stochastic GSOM model (Khoshyaran and Lebacque, 2009).

2.2. Supply-demand approach

The notions of supply and demand functions defined in Lebacque (1996) for the classical LWR model and expanded to the case of the LWR model on nodes in (Lebacque and Khoshyaran, 2002), could be also extended to the GSOM family, as it was shown in Lebacque et al. (2007). These functions built on the fundamental diagram are essential to build monotone finite volume schemes for solving the hyperbolic system (Eq. (1)). Supply and demand functions are particularly relevant for traffic flow modeling through nodes. Furthermore, the node boundary conditions are derived from supply and demand functions. To model the node, first it is necessary to convert the supply and demand functions which are conventionally expressed in Eulerian coordinates in Lagrangian coordinates.

Consider a point $x$ separating two different traffic flow states: $(-)$ for $x^{-}$ (congested traffic flow) and $(+)$ for $x^{+}$ (fluid traffic flow). The quantities of demand and supply of the GSOM model are evaluated on the basis of the couple of the equilibrium demand $(Δ (ρ, I; x))$ and supply $(\sum (ρ, I; x))$ functions which are defined by(2) ${\begin{cases} Δ (ρ, I; x) = \max_{0 \leq r \leq ρ} R (ρ, I; x^{-}) \forall (x, t) \\ \sum (ρ, I; x) = \max_{r > ρ} R (ρ, I; x^{+}) \forall (x, t) \end{cases}$ where r is the spacing at time t corresponding to the inverse of the density and the fundamental diagram.

In the case of GSOM models, the extension of local traffic supply and demand definitions is far from being straightforward. Indeed, it has been pointed out that downstream supply depends on the upstream driver attribute (which has not already passed through the considered point).

The upstream demand δ(x,t) and downstream supply σ(x,t) at a point $x$ and time $t$ can then be updated(3) ${\begin{cases} δ (x, t) = Δ (ρ (x^{-}, t), I (x^{-}, t); x) \\ σ (x, t) = \sum (\bar{ρ} (x, t), I (x^{+}, t); x) \end{cases}$ where $\bar{ρ} (x, t) : = ℑ^{- 1} {ℑ (ρ (x^{+}, t), I (x^{+}, t); x^{+}), I (x^{-}, t); x^{+}}$ .

Due to the transport driver attribute, supply must take into account both upstream driver attribute, labeled by $I_{1}$ , and downstream driver attribute, labeled by $I_{2}$ . The modified supply for the GSOM models is as follows $Θ (ρ, I_{1}, I_{2}; x) : = \sum (ℑ^{- 1} {ℑ (ρ, I_{2}; x^{+}), I_{1}; x^{+}}, I_{2}; x)$ .

Such that Eq. (3) boils down to ${\begin{cases} δ (x, t) : = Δ (ρ (x^{-}, t), I (x^{-}, t); x) \\ σ (x, t) : = Θ (ρ (x, t), I (x^{+}, t), I (x^{-}, t); x^{+}) \end{cases}$

It means that it is needed to project the observed density at $x^{+}$ on the fundamental diagram depending on $I (x^{-}, t)$ because the immediate downstream supply depends on the perception of the available space according to the next vehicle that will pass at point $x$ .

3. Lagrangian discretization of the GSOM family

3.1. Lagrangian setting: I

For large scale road networks simulation, one important issue is how to efficiently represent the heterogenous traffic flow in conforming to macroscopic and (or) microscopic traffic models. One flexible way is encompassing vehicles in packets of vehicles based on Lagrangian discretization inspired by the Godunov scheme and describing their movement on the network (Godunov, 1959). The Lagrangian coordinate system offers advantages for the accuracy and speed of the simulation. In traditional numerical methods for traffic flow models, time and space are divided into discrete units: time steps and grid cells. The solution of the equations is then computed at each time step $Δ t$ and in each grid cell of length $Δ x$ . The disadvantage of this method is that information can go both from a grid cell to its downstream neighboring grid cell (in free flow) or it can go to its upstream neighboring grid cell (in congestion). This results in relatively slow computation and inaccurate solutions. However, once known that, in a certain model, information does not travel faster than vehicles, the Lagrangian coordinate system can be used to develop efficient numerical methods. It is well known that Lagrangian framework is particularly convenient for dealing with flows of vehicles and it is especially true in traffic flow modeling (Leclercq et al., 2007, Van Wageningen-Kessels et al., 2013).

Instead of dividing space into grid cells, vehicles are divided into groups, and their movements on the network are described. Because information does not travel faster than the vehicles or vehicle groups, information only travels from one group to its following group and never to its leading group, which results in faster and more accurate computational methods. A fast resolution of the traffic model may thus be obtained.

The GSOM model can be, therefore, transformed from Eulerian coordinates to Lagrangian coordinates. Such transformation allows to build a traffic model conforming to macroscopic and microscopic traffic models.

The common expression of the GSOM models in Eulerian coordinates $(t, x)$ is given by Eq. (1). The first fundamental variable of the GSOM family in Lagrangian form (T, N) is the cumulative number of vehicles that have passed location $x$ by time $t$ on a road section (the vehicle index) $N$ . This last variable is supplemented by a second variable which is time T. Section is partitioned into small sections (cells of length $Δ x$ ) and time into discrete time steps $Δ t$ .

If we set the following change of coordinates ${\begin{cases} N (t, x) : = \int_{x}^{+ \infty} ρ (t, ξ) d ξ \\ T : = t \end{cases} Such that {\begin{cases} \partial_{N} = - r \partial_{x} \\ \partial_{T} = \partial_{t} + v \partial_{x} \end{cases}$ where $v$ denotes the speed of vehicles, if we consider the vehicle spacing $r : = 1 / ρ$ and $ϑ$ is the speed-spacing fundamental diagram as follows. $ϑ (r, I) : = ℑ ((1 / r), I) for any (r, I) \in (0, + \infty) \times ℝ$

Thus, the GSOM model in Eq. (1) can be recast in Lagrangian form as follows.(4) ${\begin{array}{l} \partial_{T} r + \partial_{N} ϑ (r, I) = 0 on (0, + \infty) \times ℝ & Conservation of vehicles \\ \partial_{T} I = f (I) on (0, + \infty) \times ℝ & Dynamics of the driver attribute I \\ v = ϑ (r, I) & Speed - spacing fundamental diagram \end{array}$

With initial conditions ${\begin{cases} r (0, n) = r_{0} (n) on ℝ \\ I (0, n) = I_{0} (n) on ℝ \end{cases}$

It is noteworthy that the application of Hamilton–Jacobi equations in traffic flow theory is helpful to bridge the gap between both representations (Laval and Leclercq, 2013, Lebacque and Costeseque, 2014). It is known $r = \partial_{N} χ$ , where $χ (N, T)$ denotes the position of vehicle N at time T which solves the following Hamilton–Jacobi equation.(5) ${\begin{cases} \partial_{T} χ = ϑ (- \partial_{N} χ, I) \\ \partial_{T} I = f (I) \end{cases}$

To introduce time and vehicle discretization, $Δ t$ and $Δ N$ are denoted as the time and vehicle steps, respectively. $I_{n} (t) : = I (t Δ t, n Δ N) for any (t, n) \in ℕ \times Z$ where $I_{n} (t)$ represents the attribute associated to the nth vehicle.

We have the choice between two discrete models either we consider the discrete vehicle position that reads. $χ_{n} (t) : = χ (t Δ t, n Δ N) for any (t, n) \in ℕ \times Z$ where ( $χ$ , I) solves the Hamilton–Jacobi problem shown in Eq. (5) associated to Eq. (4), and $χ_{n} (t)$ is the trajectory of the nth vehicle $N (χ, t) = n$ . Notice that the physical extension of vehicle $n \in Z$ is $[χ_{n} (t), χ_{n - 1} (t)]$ , or we deal with the discrete vehicle spacing defined as. $r_{n} (t) : = r (t Δ t, n Δ N) for any (t, n) \in ℕ \times Z$ where r solves the Lagrangian GSOM model shown in Eq. (4).

In the first case, i.e., for Eq. (5) the appropriate numerical scheme of the GSOM model is defined as follows.(6) ${\begin{cases} χ_{n} (t + Δ t) = χ_{n} (t) + Δ t v_{n} (t) \\ v_{n} (t) : = ϑ (\frac{χ_{n - 1} (t) - χ_{n} (t)}{Δ N}, I_{n} (t)) \\ I_{n} (t + Δ t) = I_{n} (t) + Δ t f [I_{n} (t)] \end{cases}$

While in the second case, we would have to solve the following numerical scheme for Eq. (4).(7) ${\begin{cases} r_{n} (t + Δ t) : = r_{n} (t) + \frac{Δ t}{Δ N} (v_{n - 1} (t) - v_{n} (t)) \\ v_{n} (t) = ϑ (r_{n} (t), I_{n} (t)) \\ I_{n} (t + Δ t) = I_{n} (t) + Δ t f (I_{n} (t)) \end{cases}$

Notice that both approaches are very similar and give back the same results. Indeed, one can remark that if we have(8) $r_{n} (t) : = \frac{χ_{n - 1} (t) - χ_{n} (t)}{Δ N}$

Then Eq. (7) is simply deduced from Eq. (6). By the way, knowing the spacing at each numerical step, it is easy to compute the position of all vehicles, thanks to a leader vehicle trajectory as a boundary condition. It is worth noting that both schemes are first order schemes. The first discrete model (Eq. (6)) is an explicit Euler scheme and the second scheme (Eq. (7)) can be interpreted as the seminal Godunov scheme applied with demand and supply (Godunov, 1959).

3.2. Case of the 1-phase Colombo model

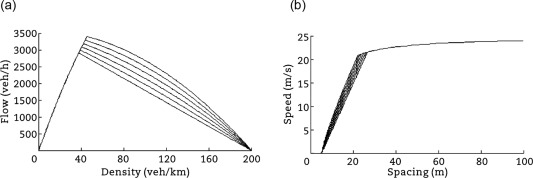
In this paper, authors have chosen for this numerical example the 1-phase Colombo model (Lebacque et al., 2007) to represent the speed function associated to the attribute $I$ for the congested phase given by(9) $ϑ (r, I) = {\begin{matrix} V_{\max} - \frac{β}{r} & r \leq r_{crit} (I) \\ (I + q_{*} r) (1 - \frac{1}{r ρ_{\max}}) & r > r_{crit} (I) \end{matrix}$ where $q_{*}$ , $β$ , $V_{\max}$ and $ρ_{\max}$ are given parameters of the model, $q_{*}$ is the theoretical maximal flow, $V_{\max}$ and $ρ_{\max}$ are respectively the maximal speed and density. The critical spacing $r_{crit} (I)$ (under which speed is (almost) null) separating the free and congested cases is computed as the inverse of the critical density $ρ_{crit} (I)$ (upper bound, beyond which traffic is congested and under which flow is maximum) as follows.(10) $r_{crit} (I) = \frac{1}{ρ_{crit} (I)}$ (11) $ρ_{crit} (I) = \frac{1}{2 (β - \frac{I}{ρ_{\max}})} [V_{\max} - I + \frac{q_{*}}{ρ_{\max}} - \sqrt{{(V_{\max} - I + \frac{q_{*}}{ρ_{\max}})}^{2} - 4 q_{*} (β - \frac{I}{ρ_{\max}})}]$ where $β$ is expressed as $β = \frac{V_{\max} - V_{crit}}{Q_{\max} / V_{crit}}$ , $Q_{\max}$ is the maximal flow.

This model corresponds to the following flow-density and speed-spacing fundamental diagrams depicted in Fig. 1.