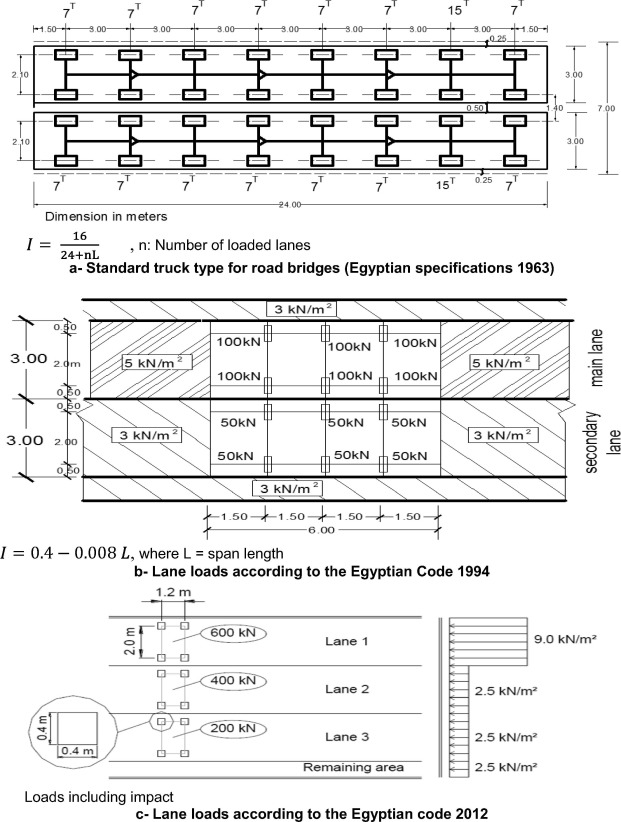
Traffic loads used in the design of highway RC bridges in Egypt

1. Introduction

Bridges form important part of a nation’s infrastructure. Maintenance and upgrading of these bridges are costly in terms of both the direct repair costs and the economic loss arising from traffic delays during repairs. In the assessment of any highway bridge structure, traffic loading is one of the most variable factors. While approaching the problem of live loads for bridges, it is necessary to make a comparison between the maximum moments in different bridge members as obtained from the codes.

Since a large amount of bridges in Egypt were built according to 1963 specifications [2] and ECP1994 [3], these bridges should be checked against the current traffic loads to ensure their structural integrity. This study focuses on the comparison of the last version of the Egyptian Code for loads (ECP 2012 [4], [5]) and the other old versions (1963 specifications and ECP1994), for concrete bridge girders, slabs and continuous bridges. The live load for bridges is represented in many ways, including an uniform load and a combination of trucks and uniform loads. The different versions of the Egyptian code for road bridge design loads are as follows:

1.
Egyptian Railway General Inspectorate of Structural Engineering (1963),
2.
The Egyptian code for the calculation of loads and forces in structural work (1994), and
3.
The Egyptian code for the calculation of loads and forces in structural work (2012). This traffic load is the load model no.1 (LM1) recommended by Eurocode 2010 [6].

Fig. 1 shows the traffic loads as given by the above three codes.

2. The parametric study

Commercial Finite Element software, SAP 2000 [8], was used to analyze a large number of concrete slab-girder bridges. The bridge consisted of a deck slab supported on a grillage system of longitudinal and transverse girders.

The deck slab was modeled as a 4-node shell element with six degrees of freedom at each node (3 translations and 3 rotations). The longitudinal and transverse girders were modeled as 2-dimensional, 2-node beam elements with six degree of freedom at each node.

Concentrated loads were applied at nodes and uniform distributed loads were applied on the shell elements.

The models studied include several parameters affecting the behavior of slab-girder bridges, especially the different rigidities in transverse and longitudinal directions.

The deck bridges analyzed consisted of a deck slab with 0.22 m thickness supported on a system of orthogonal (longitudinal and transverse) beams. Width of roadway (W = 10.5 m; i.e. three traffic lanes), four longitudinal girders with spacing = 3.5 m, width of transverse beams (0.25 m), and width of longitudinal girders (0.5 m), were all considered constant in the analysis. Also, modulus of elasticity Ec = 24.8 kN/mm2 was considered constant for all models.

Fig. 2 shows details of the studied models together with the cross and longitudinal sections for simply supported bridge models. For these models, the main parameters studied were as follows:

1.
Span of the bridge (length of longitudinal girders), the values of the span studied were 15 m, 20 m, and 25 m.
2.
Spacing of transverse beams, i.e. the number of transverse beams: 4, 5 and 6 beams with spacing 5 m.
3.
Depth of transverse beams: 0.5 m, 0.8 m, 1.0 m, 1.3 m, 1.5 m, 1.8 m, 2.0 m and 2.3 m.

Twelve two-spans continuous bridges were also analyzed, each with length; L = 25 m, roadway width = 10.5 m. Two cases of transverse beams were considered: slab on girder (no transverse beams) and transverse beams of depth = 2.3 m.

Simply supported bridges, loaded according to the codes, are shown in Figure 3, Figure 4, Figure 5 for span = 15.0 m, while loading of continuous bridges is shown in Figure 6, Figure 7, Figure 8. Detailed data for all other models are given in Ref. [7].

In addition, it was necessary to check the safety of deck slabs for bridges built during the last 50 years using old codes compared to the current version of the code. For this purpose, a total of 13 slabs were analyzed under the effect of wheel loads. The only variable studied was the rectangularity ratio of the slab; b/a, which ranged from 1.0 (square slab) to b/a

1.5. The Egyptian Code considers the deck slab as a two-way slab if b/a ≤ 1.5, where (b) is the long side of the slab (generally the spacing of transverse beams), and (a) is the short side of the slab (spacing of longitudinal beams). If b/a

1.5, the slab is considered as one-way slab with moments in one direction only. Due to the large inertia (width and depth) of the supporting girders (longitudinal and transverse) compared to the slab thickness, it is common in design to assume that the deck slab is fixed to the girders along its four edges. Bending moments in the slabs in the two directions are obtained by hand calculations.

3. Results and analysis

3.1. Simply supported bridges

For the simply supported bridges, Table 1a gives the ratios of live load maximum working moments, in both inner and outer bridge girders, as obtained using the traffic load proposed by the current Egyptian code (2012), to those obtained using both the old specifications (1963) and ECP 1994. The results are also plotted in Figure 9, Figure 10, Figure 11, Figure 12, and indicate that:

(a)
Live load moments obtained using the current Egyptian code (2012) are much higher than those obtained using the old code (1963) with a ratio MECP2012/MECP1963 ranged from 1.93 to 2.48 for outer girders and from 1.74 to 2.05 for inner ones. The lowest ratios were for bridges with large span; L = 25 m, while the higher ratios were for bridges with span L = 15 m. Since a large amount of bridges in Egypt were built according to 1963 specifications, these bridges should be checked against the current traffic loads to ensure their structural integrity.
(b)
Live load moments obtained using the current Egyptian code 2012 are higher than those obtained using ECP1994 with a ratio (MECP2012/MECP1994) ranged from 1.11 to 1.19 for outer girders and form 1.21 to 1.26 for inner ones. The higher ratios were for bridges with large span; L = 25 m, while the lowest ratios were for bridges with span L = 15 m.
(c)
The effect of transverse beam stiffness on the maximum moment of longitudinal girders was clear. Increasing depth of transverse beam caused an increase in outer girder moment and a decrease in inner girder moment. The stiffness of the transverse beam affects the distribution of load among the bridge girders. As shown in Figure 9, Figure 10, Figure 11, Figure 12, transverse beam with depth close to that of the longitudinal girder caused a reduction in moment of inner girder by 15–25% compared to the slab-on-girder bridge. However, the increase in moment of outer girder was large (up to 30% when using ECP1963) while it was only 5–10% for other codes. Also, the figures indicate that the ratio of MECP2012/MECP1963 for outer girders reduces with the increase in transverse beam depth while it remains approximately constant for inner girders.

Table 1. Maximum working moments in outer and inner longitudinal girders according to the Egyptian codes.

Bridge span L, m	Height of transverse beams, hx, m	Outer girder		Inner girder		Outer girder		Inner girder
Bridge span L, m	Height of transverse beams, hx, m	M ECP 2012/M ECP 1963	Average	M ECP 2012/M ECP 1963	Average	M ECP 2012/M ECP 1994	Average	M ECP 2012/M ECP 1994	Average
a. Simple bridges
15	No beams	2.63	2.48	2.06	2.05	1.09	1.11	1.19	1.21
	0.5	2.53		2.04		1.10		1.20
	0.8	2.46		2.01		1.11		1.21
	1.0	2.42		2.00		1.12		1.22
	1.3	2.37		1.98		1.13		1.22

20	No beams	2.44	2.24	1.90	1.88	1.12	1.15	1.21	1.25
	0.5	2.35		1.88		1.13		1.22
	0.8	2.26		1.86		1.15		1.24
	1.0	2.22		1.86		1.15		1.26
	1.3	2.17		1.87		1.16		1.28
	1.5	2.14		1.88		1.17		1.29
	1.8	2.12		1.89		1.17		1.29

25	No beams	2.06	1.93	1.77	1.74	1.16	1.19	1.23	1.26
	0.5	2.01		1.76		1.17		1.23
	0.8	1.96		1.73		1.18		1.24
	1.0	1.93		1.72		1.18		1.24
	1.3	1.90		1.73		1.19		1.26
	1.5	1.89		1.73		1.19		1.30
	1.8	1.88		1.74		1.20		1.28
	2.0	1.87		1.74		1.20		1.28
	2.3	1.87		1.74		1.20		1.28

b. Continuous bridges
25	No beams	1.41	1.33	1.18	1.12	1.23	1.23	1.24	1.24
25	2.3	1.25	1.33	1.06	1.12	1.24	1.23	1.24	1.24

3.2. Continuous bridges (Figs. 13 and 14 and Table 1b)

As discussed for simply supported bridges, the traffic load in the current Egyptian Code (2012) produced higher values of negative moment at support compared to those obtained using 1963 recommendations or 1994 code. Table 1b indicates that the average ratio M−ve 2012/M−ve 1963 was 1.33 for outer girder and 1.12 for inner one. When traffic load of ECP 1994 was used, the average ratio was 1.23 for outer girder and 1.24 for inner one.

Comparing these ratios with those obtained for simply supported bridges, the following is noted:

–
The train–type loading of 1963 traffic load produced negative moment closer to those of the ECP 2012, especially for inner girder.
–
The negative (support) moments obtained using the traffic load of 1963 specifications are close to those obtained by ECP 1994 recommendations.
–
The results also indicate that the ratio of moments obtained by different codes depend not only on the value of axle or U.D.L, but also on the configuration of these loads to each other. For example, the moment produced by U.D.L as recommended by 1963 on inner and outer girders was very small since UDL occupies only the third lane while the axle loadproduced large moments compared to those obtained using the current code 2012.

3.3. Analysis of deck slabs of slab/girder bridges

Table 2, Table 3 show a comparison between values of moments obtained using the different versions of the codes for the two-way slabs and one-way slabs, respectively. The comparison reveals that:

1.
For two-way slabs (b/a ≤ 1.5), the values of negative and positive moments in the long direction, as calculated using 1994 and 2012 recommendations, are higher than values of moments in short span. According to both codes the values of moments in long direction are about 45% higher than those in short direction for b/a = 1.43. The ratio of Mlong/Mshort increases with the increase of b/a; this ratio was 1.00–1.15 for square slabs (b/a = 1.0) for the two codes. However, the moments obtained using the traffic load of 1963 specifications were higher in the short span than in the long span, as common in the classical theory of plates subjected to uniform or patch loading. For ECP 1994 traffic load, the small longitudinal distance between axes (1.5 m) allowed the use of three axles along the long span (b) which results in covering the long span with uniform loading, producing large values of moments. For ECP 2012 traffic load, the dimensions of contact area in long span were about twice that in the short span, which may be the reason for obtaining large values of moment in the large span.
2.
According to the Egyptian code, the final distribution in one-way slabs depends on both span and the ratio of the secondary steel (in the long direction) to the main steel (in the short direction). In Table 3, the values of moments were calculated for the maximum ratios allowed by the code (A′s/As = 2/3), and for any other ratio, the values of moments will change.
3.
For two way-slabs, negative moments in short direction obtained using the traffic load of the current ECP 2012 were much higher than those obtained using traffic load of 1963 specifications by 56–80%. The highest ratio was obtained for the slabs with b/a = 1.43. However, for positive moments the above ratios of increase were 60–90% with the large ratios for slabs with b/a = 1.43.
4.
The moments in the short direction for the two-way slab as obtained by ECP 2012 were higher than those obtained using ECP 1994 by only 6–17% for negative moments and by 13–22% for positive moments.

Table 2. Comparison of maximum moments of two-way slabs.

Dimensions a × b (m)	b/a	ECP 2012/ECP 1963
		Short direction		Long direction
		M−ve	M+ve	M−ve	M+ve
a
3.0 × 3.0	1.00	1.56	1.62	2.50	2.21
3.0 × 3.5	1.17	1.64	1.70	2.67	2.32
3.0 × 4.0	1.33	1.63	1.74	2.79	2.43
3.5 × 3.5	1.00	1.68	1.78	2.87	2.56
3.5 × 4.0	1.14	1.69	1.80	3.03	2.68
3.5 × 4.5	1.29	1.75	1.86	3.07	2.73
3.5 × 5.0	1.43	1.80	1.91	3.18	2.84
4.0 × 4.0	1.00	1.62	1.75	2.96	2.62
4.0 × 5.0	1.25	1.70	1.84	3.09	2.78
4.0 × 6.0	1.30	1.75	1.88	3.19	2.89

Dimensions (m)	b/a	ECP 2012/ECP 1994
		Short direction		Long direction
		M−ve	M+ve	M−ve	M+ve
b
3.0 × 3.0	1.00	1.17	1.22	1.31	1.31
3.0 × 3.5	1.17	1.12	1.16	1.22	1.22
3.0 × 4.0	1.33	1.08	1.15	1.12	1.15
3.5 × 3.5	1.00	1.15	1.22	1.31	1.35
3.5 × 4.0	1.14	1.11	1.18	1.23	1.26
3.5 × 4.5	1.29	1.07	1.13	1.11	1.17
3.5 × 5.0	1.43	1.06	1.13	1.05	1.12
4.0 × 4.0	1.00	1.13	1.23	1.32	1.35
4.0 × 5.0	1.25	1.03	1.12	1.11	1.18
4.0 × 6.0	1.50	1.00	1.08	1.06	1.12

Table 3. Comparison of maximum moments of one-way slabs.

Dimensions (m)	b/a < 1.5	ECP2012/1963		ECP2012/1994
Dimensions (m)	b/a < 1.5	M−ve	M+ve	M−ve	M+ve
2.5 × 4.0	1.60	1.52	1	1.63	1.61
3.0 × 5.0	1.67	1.38	1.55	1.55	1.48
3.5 × 5.5	1.57	1.27	1.45	1.44	1.39

The heavy wheel loading for ECP 2012 and the presence of four wheels on the slab distributed on a small contact area, may be the reasons for obtaining high values of moments when compared to ECP 1994 and 1963 specification.

5.
A large difference was obtained between the value of moments in the long direction of the two–way slabs using ECP 2012 and those obtained using 1963 specifications. ECP 2012 values were higher by 2.5–3.19 times the moments obtained by the old code (1963). However, when ECP 2012 values were compared with those of ECP 1994, the ratio of M−ve 2012/M−ve1994ranged 1.05–1.32, and the lowest ratio was for slab with b/a = 1.43.

Similarly, for one-way slabs, ECP 2012 results were higher than those of 1963 by 27–52% (for negative moments) and by 45–72% (for positive moments), and the above ratios were 44–63% and 39–61% when compared to 1994 code.