A Systematic Literature review for the rig scheduling problem: Classification and state-of-the-art

1. Introduction

The exploration and production (E&P) of oil and gas involves several complex, expensive, and high-risk operations (Suslick and Schiozer, 2004). One of the most critical phases of the E&P is well construction and maintenance, which relies mainly on rigs. Such rigs are typically costly and scarce resources, for which daily rate can vary between US$ 50,000 and US$ 700,000, depending on the rig type, market, and operational specifications (Kaiser, Snyder, 2013, Osmundsen, Roll, Tveterås, 2010). In general, companies hire rigs to perform essential well operations such as drilling, evaluation, completion, and workover. An undersized fleet of rigs can result in oil production delays that affect the profitability of the wells. On the other hand, an oversized fleet may lead to high idleness and opportunity costs. Consequently, rig fleets must be appropriately planned and scheduled to ensure that the rigs will be available at the right place at the right time with the lowest possible cost.

However, the decision-making comprising the rig scheduling problem (RSP) is highly complex, as it involves numerous widely varied tasks from different phases of the E&P (Tavallali et al., 2016). Operations are subject to risks in geological prospects, economic evaluations, development, and production (Suslick et al., 2009). Moreover, several techniques from interdisciplinary areas might be applied to the RSP (Khor et al., 2017). Many studies aiming at supporting those companies have been made using quantitative and analytical methods, such as mathematical programming, heuristics, and data science techniques, including some literature reviews. The RSP involves multiple dimensions of the E&P and different solution techniques, making it arduous to identify research gaps, opportunities, and trends.

An essential contribution of this integrated literature review is to propose a proper classification of the RSP, considering the various perspectives, levels, and aspects of the RSP. To the best of our knowledge, only a few literature reviews on this topic are available, being either outdated or focusing only on particular dimensions of the RSP (Bissoli, Chaves, Ribeiro, 2016, Tavallali, Karimi, Baxendale, 2016, Khor, Elkamel, Shah, 2017).

Moreover, the lack of a standardized classification for the RSP is a critical shortcoming in the available literature. Against this backdrop, this paper proposes a new taxonomy and presents an extensive and systematic literature review of the RSP. With the purpose of supporting future studies, this analysis also describes the current gaps in the RSP literature and trends. By assembling this literature review, our goal is to find answers to the following research questions:

•
How can we classify the different dimensions of the RSP under the perspective of available case studies and solution approaches?
•
How the RSP has been most often addressed in the literature, both from academic and industrial perspectives?
•
What are the trends that can be observed after analyzing the literature related to the representation of the RSP in terms of modeling choices and analytical methods?
•
What are the main gaps between the academic literature and industrial practice?

2. Problem description

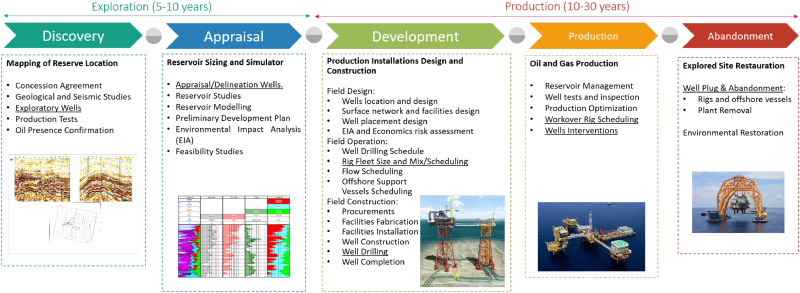
The RSP plays a central role in the decision-making of the supply chain of the oil and gas sector. The exploration and production (E&P) can take many years, and it is a crucial part of the process to the company’s profitability. As mentioned by Baker (1996), IFP School (2015), and Pereira (2005), the E&P can be separated into five main phases:

(1)
Discovery phase: mapping of possible oil fields with geological and seismic studies and the drilling of exploratory wells to confirm the presence of hydrocarbons;
(2)
Appraisal phase: after the oil presence confirmation, delineation wells are drilled and reservoir modeling studies are performed to estimate the properties, size, value of the reserve, and its techno-economic development feasibility;
(3)
Development phase: comprising essential activities and production decisions, including field design (well location and type, surface network, and facilities design), field operation planning (well drilling scheduling, flow scheduling, rig fleet scheduling, and offshore logistics), and field construction (facilities fabrication and installation, well construction, drilling, and completion);
(4)
Production phase: can extend through decades and has many different successive phases to increase productivity, correct oil flow loss, and solve mechanical failures;
(5)
Abandonment phase: when the hydrocarbon production rate becomes economically infeasible and the reservoir is abandoned.

Fig. 1 describes the aforementioned phases and their significant decisions, in which the underlined ones are related to the RSP.

From the oil discovery to the field abandonment, rigs are used to drill, complete, maintain, and abandon wells, as shown in Fig. 1. In the discovery phase, exploratory wells are drilled using rigs to confirm hydrocarbon presence. Then, in the appraisal phase, delineation wells are drilled to estimate the reservoir properties. In the development phase, wells injecting water, fluids, or gas into the reservoir (injection wells) and wells retrieving oil or gas from the reservoir (production wells) are drilled and completed also using rigs. In this phase, the rig fleet size is decided, as well as the operation schedules of the rigs. While in the production phase, completed wells often require workover rigs to perform an intervention aiming to increase productivity, correct oil flow losses, and solve mechanical failures. Finally, wells must be plugged and abandoned (a process in which wells are abandoned and cannot be used again after the installation of well barriers or plugs), which is often performed using rigs. Each of these operations requires a specific rig type (Bakker et al., 2017). In what follows, we describe the different types of oil rigs and their purpose.

2.1. Oil rigs

As pointed out earlier, the rigs are one of the primary resources used in the exploration of oil and gas. These highly complex and expensive structures are used in critical activities such as evaluation, drilling, completion, and workover. There are several types of oil rigs, each one with a specific purpose in terms of operations it can perform and its own technical specifications. Fig. 2 presents the different types of oil rigs.

As shown in Fig. 2, the main classification is according to the location of the well, which can be onshore or offshore (Al-Azani, 2014). According to Bourgoyne et al. (2016), onshore drilling rigs are mainly classified based on their mobility, being either conventional or mobile rigs. The first is a fixed rig, in which the derrick is assembled at the drilling location and is the most frequently used land rig type. The second is a mobile rig coupled on wheeled trucks, allowing it to be moved between drilling facilities more efficiently. On the other hand, the most common offshore rigs are: fixed rigs (bottom-supported oil platform used until 300 m water depth); semi-submersibles rigs (floating platforms used up to 2,000 m of water depth); jack-up rigs (bottom-supported platform with elevating legs used until 150 m) and drill-ships (floating platforms constructed in a vessel hull used up to 2,000-meter water depth) (Petrobras, Markit, Al-Azani, 2014, Baker, 1996).

2.2. The rig scheduling problem

Generally, an oil and gas company operates many oilfields and wells simultaneously, each one in a different E&P stage. To meet expected production and delivery dates, well activities must be adequately scheduled and allocated to rigs, aiming to avoid delays and optimize the use of resources (Eagle, 1996). This decision-making is called the Rig Scheduling Problem (RSP).

In essence, the RSP considers a set of wells (e.g., onshore or offshore, injection or production), a set of tasks (drilling, completion, or workover; note that the terms operation, activity, and job are used interchangeably in this context) that have to be executed on these wells and a set of resources (onshore or offshore rigs) available or to be hired to perform these activities. Usually, the objective is to provide a schedule that minimizes the total costs or the total oil production loss, considering a list of operating and engineering constraints and assumptions (Tavallali et al., 2016).

The RSP can be classified according to several characteristics involving the problem setting (oil field location, well operations, field development integration, resources considered) or the approach (how the problem is addressed and solved: modeling, rig fleet, single/multiple jobs, and type of objective functions). The setting attributes refer to characteristics of the problem that may have implications for the approach, attributes connected with the oil and gas exploration and production. And the approach refers to how the problem is being modeled and solved, attributes related to the technique and modeling. Fig. 3 presents our taxonomy for the RSP.

The first division of the RSP is according to the oilfield location: onshore or offshore. Onshore well operations are generally more straightforward, faster, and less expensive than offshore well operations, as the latter is a more complex and high-risk environment (Bassi et al., 2012). The problems also vary according to the types of rig operations that are scheduled. Some studies consider drilling activities, while others focus on the completion, which are interventions to prepare the well for production after being drilled. Also, some papers consider problems with workover activities, which consist of well interventions performed after their completions (Holmager, Redda, 2013, IOM3).

Rig scheduling is a multidimensional decision task related to several planning levels of the E&P. Most studies tackle rig scheduling as an independent decision-making process; we refer to this planning level stand-alone. However, some studies have an integrated field development planning, considering other problems such as reservoir modeling, field design, facilities locations, and production scheduling. Similar behaviors were noticed by Lasschuit and Thijssen (2004) in planning and scheduling of the downstream of the oil and gas sector. The more decisions are considered, the harder it will be to solve the problem. Rig operations involve multiple resources and thus, another classification is possible, according to the planned resources. Usually, only rigs are considered in the planning. However, some studies have also considered crews, pieces of equipment, and other vessels.

In some studies, the wells are physically close to each other and the operations have processing times that are much longer than the traveling time between the wells, precluding the need of taking into account routing considerations in the planning process. Therefore, the RSP can also be classified according to the employment of routing techniques, dividing the problems into: scheduling-only (or simply scheduling) problems, in which the traveling times between wells are negligible; and routing and scheduling (to which we refer simply as routing hereinafter, presuming that the scheduling activities are implied by context), when the rigs transportation costs are significant and vary between wells, and thus routing decisions have also to be considered (Bissoli et al., 2016). Usually, routing and scheduling problems are classified according to the fleet of vehicles or the set of machines (resources) available (Georgiadis, Elekidis, Georgiadis, 2019, Eksioglu, Vural, Reisman, 2009). The fleet of rigs can be homogeneous, when all rigs share the same costs, processing times, technical specifications, and so forth, or heterogeneous, meaning that the rigs possess different characteristics and might be capable of performing specific operations or require particular well conditions. According to the level of complexity of the problem, a well might have more than one operation to be executed, or the rigs may consider operations with different characteristics, as in Hasle et al. (1996) and Fernández Pérez et al. (2018). Therefore, another RSP classification depends on the number of jobs: whether a single job for each well is considered or multiple jobs from the same well are allocated to the rigs.

Another critical attribute is the objective function that will be optimized. The problem can consider a single objective (when there is only one objective to be optimized) or be multi-objective (when there are multiple objectives to be optimized). As to the nature of the objective function, it can be a non-monetary indicator (such as completion time, tardiness, distance traveled, number of rigs used, wells served), a monetary indicator (total costs, net present value, cash flow), or an oil-related indicator (oil production, oil production loss or expected oil recovery).

Analyzing the RSP literature according to the aforementioned characteristics, similarities between the papers were observed, enabling us to gather them in four major classes of problem:

(1)
Drilling Rig Scheduling Problem (DRSP): refers to drilling and completion rig scheduling problems in a stand-alone planning level, when the rig scheduling is an independent decision from the rest of the field development problems. Drilling and completion usually take place in the development of non-completed (new) wells and the goal is to minimize the rigs fleet costs meeting a due date for the wells to start oil production. Some DRSP problems consider a well to have a single job to be performed while others consider multiple jobs for each well;
(2)
Workover Planning: problems in which the rigs are used in workover operations. These operations occur in the production phase, when existing and completed wells require maintenance or rework to be performed. As a result, this decision-making is usually separated from the other rig-related decisions and there is only a single job (a single maintenance) to be scheduled for each well. It can be divided according to the use of routing in two sub-groups: workover rig scheduling problems (WRSPs) and workover rig routing and scheduling problems (WRRSPs);
(3)
Field Planning (FP): refers to problems in which the rig scheduling is integrated with other field development decisions, such as reservoir modeling, field design, and production flow scheduling. In these cases, the RSP depends on or influences other decisions related to the oilfield development. For instance, the location of the platforms influences the duration of the drilling and the traveling time between the platforms, which are in turn crucial parameters in the RSP. On the other hand, the rig scheduling affects the well production schedule, as the well can only start producing after being drilled and completed. Usually, these problems aim to maximize the net present value (NPV) of the oilfield;
(4)
Resource Planning (RP): the rig scheduling problem is integrated with the planning of other resources that also affect the decision or are affected by the RSP, such as offshore support vessels (OSVs), equipment, and crews. For instance, many OSVs vessels are used to lay pipes connecting the wells and platforms. As noted by Abu-Marrul et al. (2020), the connections can only start after the drilling and completion of the well. Also, all rig operations demand the use of other resources, such as equipment and crews. To assure that the equipment and crews will be available on time to execute the rig tasks, it is important to consider the inventory level (equipment) or schedule (crew) within the RSP. This supply chain perspective usually aims to minimize the logistic costs of the operations.

This classification and the taxonomy in Fig. 3 answer our first research question: How can we classify the different dimensions of the RSP under the perspective of available case studies and solution approaches?. Next, we present the methodology used to assemble this literature review of the RSP.

3. Methodology

This systematic literature review (SLR) was executed based on a step-by-step method adapted from Thome et al. (2016), which can be divided into: (i) research delineation; (ii) literature search; (iii) data collection; (iv) data analysis; (v) interpretation. This complete SLR process is illustrated in Fig. 4, in which green labels represent the outputs of each step.

The first step was the research delineation, the problem description in the previous section, and the methodology definition (current section). In the second step, we have chosen to use Scopus and Web of Science (WOS) as the primary search databases. Aiming to define the most common keywords, a collection of benchmark RSP studies was manually selected and their titles, keywords, and abstracts were analyzed. As mentioned earlier, one of the main contributions of this paper is to propose a taxonomy and classification for the RSP that can be used in its different dimensions and decision levels. This literature gap can be observed through our SLR and especially after analyzing the selected RSP papers. With the help of a word cloud plot (shown in the Appendix), using titles, keywords, and abstracts, we selected a search query that was simultaneously broad to avoid limiting results and limited to avoid too many unwanted results. This search query combines the following keywords: scheduling, rescheduling, routing, mobilization, move, programming, simulation, optimization, model, algorithm, heuristic, procedure, technique, system, well, oil, petroleum, onshore, offshore, workover, drilling, completion, downhole, reservoir, evaluation, rig, and vessel. No specific time frame was considered, and all articles found have been included as long as an online version of the paper could be found. The complete search query is presented in the Appendix.

This search query was executed on the Scopus and WOS databases on $27^{t h}$ November of 2020, resulting in 3248 papers from Scopus and 551 documents from WOS. By reviewing of titles, keywords, and abstracts, 3130 and 459 documents were eliminated from Scopus and WOS, respectively. The elimination criteria used was to select only papers that consider routing or scheduling of oil rigs and written in English or Portuguese. This large number of unwanted papers is a direct consequence of the lack of a robust classification and taxonomy system for the RSP, which this SLR tries to address. The 118 (Scopus) and 92 (WOS) resulting articles were read and 52 (Scopus) and 60 (WOS) documents were eliminated from the review. After joining the 98 documents found in Scopus and WOS, 27 duplicated papers were eliminated, culminating in the selection of 71 papers. The articles cited by them were searched using Google Scholar and Scopus databases, and 69 new documents were appended to the list, of which just 16 and 9 were actually in Scopus and WOS, respectively. Then, the papers citing the selected papers in Google Scholar and Scopus databases were read and 50 new studies (13 from Scopus and 4 from WOS) were found. Last, 61 documents were eliminated after a more profound analysis to double-check the selection, resulting in 130 papers, of which 68 and 35 were available in Scopus and WOS Databases, respectively. During this process, some literature reviews were found: Bissoli et al. (2016), Tavallali and Karimi (2014), Tavallali et al. (2016), and Khor et al. (2017). We chose to exclude these papers from the final selection as they do not specifically propose a new method, model, or case study. Table 1 summarizes these literature reviews, their scope, number of studies revised (RSP and total), and the time frame (the years considered). The literature reviews with asterisk did not count how many papers were being revised, but the total number was bigger than 100. As none of them did a systematic literature review and many classes of the RSP were not considered, the number of RSPs revised by them is considerably smaller than the number of publications found using our methodology. Their results will be compared with our findings later on.

Table 1. Summary of the others literature reviews found.

Literature Review	Main goal	Papers revised (RSP)	Papers revised (total)	Years
Tavallali and Karimi (2014)	Field planning, development decisions and process system perspectives	9	48	1990–2014
Tavallali et al. (2016)	Field planning, development decisions and process system perspectives	8	100*	1990–2016
Bissoli et al. (2016)	Workover planning, its drivers and vehicle routing perspectives	33	64	1977–2015
Khor et al. (2017)	Optimization methods for field development problems	13	100*	1972–2017

For the third step (data collection), the papers were thoroughly examined. With the support of the classification presented in the previous section, the data was gathered in a table with the essential information. Other data, such as co-citation networks and keyword occurrence, were manually generated and assembled in bibliographic citation files.

The fourth and fifth steps, data analysis and interpretation, are presented in the following sections. Qualitative and quantitative content analyses were performed with the assist of the following tools: CitNetExplorer® (a software for bibliography analysis, co-citation and keyword analysis of the papers), R (a programming language and free software environment used for statistical computing and graphics), Excel® and Tableau® (an interactive data visualization software).

4. Literature review

The use of Operations Research and quantitative methods in oil rig scheduling dates back to the 1960s when Aronofsky and Williams (1962) and Aronofsky (1962) proposed two linear models for oil production planning. At that time, these models required substantial computational resources, preventing any practical application to the problems (Pittman, 1985). As a result, most developments concerning rig scheduling employed approximation techniques (Barnes et al., 1977) and decision-making rules (Cochrane, 1989). The body of research around the topic only started to fully develop in the 1990s with the improvement in computational capacity and optimization methods, as shown in Fig. 5.

It is possible to observe in Fig. 5 that there is a significant growth of workover rig planning (scheduling/routing and scheduling) research in the early 2000s. This particular growth is mainly due to the interest of Brazilian researchers and industry stakeholders in the problem, for which we can identify three main reasons. First, the Brazilian Petroleum Investment Law mandates that part of the royalties of oil and gas exploration and production is invested in research and development applications (Pessôa Filho et al., 2006). Second, during the 2000s and 2010s, major oil fields were discovered in Brazil, leading to a significant growth in its oil production and, consequently, in the investments in research (Iachan, 2009). Finally, the Brazilian exploration and production of oil and gas are concentrated within the state-owned company Petrobras, which used to hold a monopoly in the Brazilian downstream and midstream supply chain (Iachan, 2009). As a result, Brazil is one of the main rig markets, with 57 active rigs in 2011, of which 10 are owned by Petrobras (Kaiser and Snyder, 2013). This large fleet of active rigs poses significant challenges concerning its planning. Consequently, with the massive amount of investments in research and operations optimization, many rig scheduling studies were published by authors affiliated with Brazilian institutions, as shown in Table 2. Also, it is possible to observe that other petroleum-producing countries have a large number of publications. The values in Table 2 were calculated by summing the number of authorship from each country in each study.

Table 2. Author affiliation’s country distribution for the rig scheduling problem.

Author’s Country	Number of Publications
Brazil	144
USA	78
Norway	24
Argentina	20
United Kingdom	14
Canada	13
Saudi Arabia	11
United Arab Emirates	10
Iran	8
Austria	8
India	6
France	6
Indonesia	5
Others	17

Regarding the type of publication, the majority of studies was from conference proceedings. However, there is a significant volume of papers published in journals (49), as shown in Table 3.

Table 3. The number of rig scheduling publications per type of study.

Type	Publication
Conference	56
Journal	49
Master Thesis	10
Doctoral Dissertation	7
Book	4
Graduate	2
Tech Report	1
Book Chapter	1

Using the CitNetExplorer® software, we developed the citation network of the rig scheduling publications found in the literature review shown in Fig. 6. Studies without any citation link were omitted from the chart for the purpose of clearance and clarity. The four major groups are marked in the chart: Drilling Rig Scheduling (green labels); Workover Planning (blue labels); Resource Planning (purple labels); and Field Planning (orange labels).

The citation links in Fig. 6 are also helpful to understand the connection between these RSP groups. For instance, workover planning problems are highly centralized and connected, suggesting a greater level of discussion inside the literature. As expected, the drilling rig scheduling problems are closer to the workover planning problems, as these two groups share many modeling similarities. The integrated problems, resource planning and field planning, are more scattered, as these problems are more diversified. Next, we study each of these groups, analyzing how the research outputs evolved and answering the second research question of How the RSP has been addressed in the literature.

4.1. Drilling rig scheduling problem

Aronofsky and Williams (1962) and Aronofsky (1962) were the first known studies addressing the RSP using linear programming. They proposed a model for scheduling the oil production curve under a fixed drilling rig schedule and another one to schedule rigs and drilling tasks under a predefined production. Hartsock and Greaney (1971) developed a mixed-integer non-linear programming (MINLP) inventory model for optimizing the drilling schedule of an oilfield considering the rigs operation and transportation costs. Benefiting from the improved computational resources made available since then, Haugland et al. (1991) proposed a linear programming model for allocating fixed and movable offshore rigs to routes maximizing the net presented value (NPV). Gutleber et al. (1995) presented a fuzzy ranking method used in the drilling schedule. One year later, Eagle (1996) used a simulated annealing (SA) algorithm to schedule drilling rigs and to maximize NPV in a multi-period horizon.

A decade later, Irani (2007) described a system implemented in a Mexican oil company that allows real-time managing and visualization of the rig schedule and the drilling tasks. Irgens and Lavenue (2007) and Irgens et al. (2008) used a stochastic local search to maximize oil production and provide real-time visualization to schedule a heterogeneous fleet of drilling rigs. Meanwhile, a drilling rig fleet sizing model was proposed by Husni (2008) for scheduling oil projects using linear programming and a genetic algorithm (GA) with a greedy heuristic (GH). Glinz and Berumen (2009) presented a mathematical programming model to schedule drilling resources. Falex (2009) proposed a GA to the drilling rig scheduling problem with heterogeneous fleet that minimizes the rigs hires and oil production loss. Addressing a real study case of an Emirati oil company, Sumaida et al. (2013) presented a systematic methodology for manually routing onshore rigs. Amrideswaran et al. (2015) presented a framework for risk assessment in workover and plug and abandonment (P&A) operations in which offshore rigs are scheduled according to a GH, based on a priority ranking matrix. Another systematic approach was later proposed by Arnaout et al. (2017) focusing on the operational perspective of onshore drilling RSP. Amer et al. (2016) described a system for scheduling and managing a fleet of drilling and workover rigs with feasibility validation over a master schedule.

Some authors combined simulation and optimization techniques for RSP. Flager (2014) proposed a multi-objective GA with Monte Carlo simulation to schedule a heterogeneous fleet of onshore drilling rigs maximizing oil production and minimizing its cost. Zahran and Al-Fardan (2014) proposed an automated system for scheduling and routing rigs that used both simulation and optimization algorithms.

Meanwhile, other studies focused on mathematical formulations and solving techniques. Gonçalves (2009) used a GA for the drilling rig routing and scheduling problem, taking advantage of the ease of GA modeling to introduce complex constraints, such as environmental and regulatory laws and rigs displacement costs. Al Gharbi (2011) addressed the routing and scheduling of a homogeneous fleet of onshore drilling rigs and proposed a heuristic based on the Dijkstra algorithm. Haugland and Tjøstheim (2015) presented alternative linear programming formulations for scheduling and routing a heterogeneous fleet of offshore rigs. First, they introduced a model for drilling and location decisions. As an alternative method, the authors proposed a dynamic network flow model for rigs moving and drilling decisions. Chowdhury (2016) optimized the routes and schedules of onshore drilling rigs using the program evaluation and review technique and critical path method techniques. Silva et al. (2016) proposed a mixed-integer programming (MIP) model for the rig routing and scheduling problem of a heterogeneous offshore fleet, minimizing the production loss and the rig utilization costs. They tested their approach considering a small instance with a variety of tasks and realistic assumptions, resulting in non-linear constraints.

Aiming to address technical and economic constraints, Tavallali and Zare (2018) proposed a mixed-integer linear programming (MILP) model for routing and scheduling the drilling activities on a fleet of owned/hired rigs, minimizing drilling costs, rigs movements costs, and hiring costs and considering eligibility, rig’s contract length, and others constraints. Using advanced techniques of the VRP literature, Kulachenko and Kononova (2020) presented a Variable Neighborhood Search (VNS) based matheuristic in which a MILP solver is used to optimize the well-drilling work distribution and the VNS solves the routes.

A decision support system was presented by Carrilho and Villas Boas (2016) for the RSP. It uses a MILP model to maximize the tasks allocation to the rigs already hired and minimize the fleet of rigs to be hired. To reduce computational requirements, the authors considered the jobs in blocks and the time horizon in weeks. Using this block structure, Santos (2018) presented two models for the offshore RSP, one for minimizing the fleet of rigs and another minimizing its costs. Some local searches, constructive heuristics, and matheuristics were also developed and tested in real-life instances. However, most methods required considerable computational effort as result of the time-indexed formulation considering long-term planning horizons. An alternative formulation for the time-indexed parallel machine scheduling was introduced by Carrilho et al. (2018), based on bucket-indexing. This time formulation divides the planning horizon in periods of equal length (buckets with a size that can assume values between 1 and the shortest processing time of jobs) and achieved promising results that enable realistic rig scheduling models for large instances with long planning horizons.

A trend that has become popular since 2015 is the use of machine learning and data science techniques to support optimization algorithms, also known as data-driven optimization. Ma et al. (2018) proposed a method that uses a data mining system for extracting key information from daily drilling reports and historical data, converts and aggregates it in a database, identifies drilling opportunities, and uses it to optimize the short-term rig schedule. Castiñeira et al. (2018) used machine learning and natural language processing (NLP) for an automated analysis of drilling data. The historical data was then used to optimize the rig schedule through heuristics, maximizing NPV and oil production. Both studies have used advanced machine learning techniques, but the optimization methods and formulation are not defined in sufficient detail, preventing us to compare them with others formulations. A summary of the total of the DRSP studies discussed in this section is illustrated in Fig. 15 in the Appendix.

4.2. Workover rig scheduling problem

Barnes et al. (1977) investigated the workover rigs scheduling problem and proposed two approximate techniques to minimize the oil production loss, testing it on a small and short-term instance. Decades later, several other papers addressing the WRSP were published. Noronha and Aloise (2001) presented a GH for planning operations in onshore rigs that minimizes not only the oil production loss but also the environmental risks. Aloise et al. (2002) tested variations of ant colony with path-relinking (AC-PR) against a GA and a greedy randomized adaptive search procedure (GRASP). Gouvêa et al. (2002) proposed two evolutionary heuristics for scheduling workover operations in a homogeneous fleet of onshore rigs: a transgenetic algorithm (TA) and a memetic algorithm (MA). Maia et al. (2002) compared a simplified tabu search (TS)-based heuristic with the heuristics from Gouvêa et al. (2002) and Aloise et al. (2002). The AC-PR remained achieving the best results. According to Bassi (2010), this study was related with a geo-referenced computational system for workover onshore rigs management that was also discussed in Maia et al. (2002), Gouvêa et al. (2002), Aloise et al. (2002), and Aloise et al. (2006).

After modeling the WRSP as a binary integer linear model, Costa and Ferreira Filho (2004) created a maximum priority three-criteria heuristic (MPTH), whose simplicity allows it to be implemented in simulations and sensibility analysis. Later, Costa and Ferreira Filho (2005) tested a dynamical assemble heuristic (DAH) that overperformed the MPTH even in large examples. These two methods can also be found in Costa (2005), which also presents a GRASP and 300 real-life instances for the problem.

Several other authors used these instances later and tested them with different solution algorithms: a GA (Alves and Ferreira Filho, 2006); a scatter search (SS) by Oliveira et al. (2007) and Lorenzoni and Polycarpo (2010); a bubble swap (BS) by Pacheco et al. (2009a); a GA-2opt (Douro and Lorenzoni, 2009); a GRASP-PR from Pacheco et al. (2009b) and Pacheco et al. (2010); a simulated annealing (SA)-based heuristic from Ribeiro et al. (2011); a memetic algorithm (MA) from Pacheco (2011). The greedy randomized adaptive search procedure with path-relinking (GRASP-PR) from Pacheco et al. (2009b) and Pacheco et al. (2010) was based on Costa (2005)’s GRASP. To achieve better solutions for the WRSP, Lorenzoni and Polycarpo (2010) enhanced the SS (Oliveira et al., 2007) using MPTH as a solution generator and found 11 new best solutions. Ribeiro et al. (2011) tried to solve the WRSP’s harder instances, proposing a simple, yet robust, simulated annealing (SA)-based heuristic to generate an initial solution and apply the SA iterative, ultimately outperforming DAH, GRASP, GRASP-PR, SS, BS, GA-2opt and MA.

A few variations of the WRSP can be found in the literature. Specifically, Lasrado (2008) created an application based on a manual methodology that adapted the reservoir simulation technique from de Andrade Filho (1994) to generate schedules and to minimize the number of rigs and traveling distances, reducing transportation and contract costs. Marques et al. (2014) presented a decision support system that uses a MILP model to size and to schedule homogeneous offshore rigs, minimizing the fleet size and maximizing its utilization.

Meanwhile, Monemi et al. (2015) addressed the heterogeneous WRSP, proposing a new MILP model based on arc-time-indexed formulations and two solution techniques: branch-price-and-cut (BPC) and hyper-heuristic (HH), which found near-optimal solutions with just a few seconds. Danach (2016) also tackled this problem with a (1,0)-linear programming model and a HH using algorithms for construction, local search, perturbation, and reconstruction. The HH was tested in a real case and faced difficulties to solve large instances. Hence, future works on the mathematical formulation were suggested by the authors to improve its efficiency.

Aiming to achieve better solutions, Pérez et al. (2016) proposed a decomposed reformulation of the (1,0)-linear model from Costa and Ferreira Filho (2004) for the WRSP of homogeneous onshore rigs that had fewer variables and constraints and was tested in the instances of Costa (2005), finding new exact solutions for large instances and outperforming the heuristic methods. Based on their model, Fernández Pérez et al. (2018) and Pérez et al. (2019) presented deterministic and stochastic models for the WRSP to fleet size and to minimize the oil production loss and rig fleet costs. The authors adapted the instances from Costa (2005), Paiva (1997), Soares et al. (2011), Ribeiro et al. (2012a), and Bissoli (2014), testing it with several scenario generation methods, including Monte Carlo simulation, scenario reduction, and Quasi-Monte Carlo, and achieving robust solutions even for large instances. A summary of the number of WRSP studies discussed in this section is illustrated in Fig. 16 in the Appendix.

4.3. Workover rig routing and scheduling problem

Building upon advances in vehicle routing problem formulation and solution techniques, Paiva et al. (2000) proposed a SA, based on Paiva (1997), for the workover rig routing and scheduling problem minimizing rigs expenses and oil production losses. Since then, many other authors have tackled the homogeneous WRRSP with several heuristics. Rocha et al. (2003) presented 3 variations of variable neighborhood search to the WRRSP, obtaining the best results with a cooperative parallel VNS (CPVNS) with PR. Trindade and Ochi (2004) proposed 6 variations of GRASP-PR, later enhanced by Trindade (2005) and Trindade and Ochi (2005) to a hybrid GRASP-PR. To improve the GRASP-PR efficiency, Neves (2007) and Neves, Ochi, 2006, Neves, Ochi, 2007 presented a GRASP with adaptive memory (GRASP-AM) and tested it against other heuristics such as TS and iterated local search (ILS). Ribeiro et al. (2012b) compared this ILS with a clustering search (CS) and an adaptive large neighborhood search (ALNS). In this study, the ALNS outperformed the other methods. Finally, Shaji et al. (2019) proposed a new aggregated rank removal heuristic (ARRH) to the ALNS (Ribeiro et al., 2012b) and compared it with others heuristics: VNS (Aloise et al., 2006); GA; GA with VNS (GA+VNS) and ALNS (Ribeiro et al., 2012b). These heuristics were tested in some theoretical instances, in which the ARRH based ALNS outperformed the other methods.

Some authors focused on new formulations for the homogeneous WRRSP. Sabry et al. (2012) proposed a new MILP formulation minimizing oil production and rig operation costs for a company that owned a dedicated rigs fleet and could hire additional rigs. The authors tested their model considering a short-term theoretical instance using a MA and GRASP. Duhamel et al. (2012) proposed three models and hybrid methods for onshore workover rigs aiming to minimize the total production loss: a MILP model based on Aloise et al. (2006); an open vehicle routing problem (OVRP) strategy with lifted constraints and better bounds; and a set-covering formulation, obtained through a Dantzig-Wolfe decomposition of the OVRP and enhanced using column generations with GRASP and VND. Last, Kromodihardjo and Kromodihardjo (2016) used a discrete simulation software to propose exhaustive search and combinatorial algorithms for the WRRSP, obtaining near-optimal or optimal solutions in small instances based on real data.

Another variation of the WRRSP is to consider a heterogeneous fleet of rigs. Aloise et al. (2006) addressed this problem using a VNS that mixes several swap and insert moves (e.g., changing the wells allocated to a rig or allocating different rigs to a well). The problem was tested in real-life instances and later implemented in a Brazilian oil company, generating potential savings of US$2.5M per year. Soares et al. (2011) analyzed the characteristics of the WRRSP and proposed constructive heuristics and a new objective function minimizing the rigs fleet cost. Meanwhile, Ribeiro et al. (2012a) tried to find exact solutions with a branch-price-and-cut (BPC) approach (based on TS, column generation, ng-path-relaxation, and subset-row inequalities) that enabled it to solve real-life examples with up to 200 wells and 10 rigs. Later, Ribeiro et al. (2014) presented a hybrid-GA (HGA) to heterogeneous WRRSP and compared it with three others methods: VNS (Aloise et al., 2006), branch-price-and-cut (Ribeiro et al., 2012a), and ALNS (Ribeiro et al., 2012b). The BPC, ALNS, and HGA were consistently superior to the VNS, having the first, faster solutions than the alternative methods, but with lower qualities than the ALNS and HGA, which in turn was the method that found all the best solutions. Last, Bissoli et al. (2014) and Bissoli (2014) also addressed the WRRSP using a bi-objective ALNS that minimizes the production loss and the onshore rig fleet size, which, according to the authors, also minimizes the total costs. However, this assumption is a simplification as, in reality, a minimal fleet does not mean that chartering costs are optimal.

A different approach to the WRRSP was proposed by Vasconcelos et al. (2017). The authors developed a genetic algorithm that uses operational historical data integrated into an optimization workflow to minimize the total non-productive time of the offshore wells served by a heterogeneous fleet of vessels with different load capacities and limited abilities. The proposed algorithm was tested on real data of a petroleum company and improved, in terms of navigation and operation time, between 20–40% of the original plan. Later, Tozzo et al. (2020) proposed a hybrid GA for the WRRSP with heterogeneous fleet minimizing oil production loss and rig fleet costs in a multi-objective perspective.

A trend in the optimization models is to consider uncertainty in the decision-making. This trend is important to RSP, which emerged from the need to consider the uncertainties related to geological concepts (structure, reservoir seal, and hydrocarbon charge), economic evaluations (costs, probability of finding, and producing economically viable reservoirs, technology and oil price), development and production (infrastructure, production schedule, quality of oil, operational costs, and reservoir characteristic), traveling time between wells and well service time (especially in the offshore fields that are subjected variable conditions such as weather and sea state) (Suslick et al., 2009).

Following this tendency, Bassi (2010) and Bassi et al. (2012) proposed a simulation-optimization approach to minimize production loss for heterogeneous offshore rigs in two phases: simulation of well service times and oil potentials; and optimization using GRASP. These phases were repeated for a significant number of times, instances, and fleet sizes, enabling to make scheduling decisions under uncertainty and to unveil the trade-off between fleet size and oil loss as a larger number of rigs results in better performance measures and higher operating costs. Bassi et al. (2012) also provide a literature review concerning workover rigs with fruitful discussions.

Most WRRSP studies consider that the decision-maker knows beforehand which wells will require intervention. However, in reality, often one cannot know with certainty which and when a well will be due maintenance. To tackle this problem, Silva and Silva (2018) proposed a dynamic approach to the WRRSP, minimizing the total oil production loss of wells that are revealed along the planning horizon, called as D-WRRSP (dynamic workover rig routing and scheduling problem). The model was based on the formulation of Ribeiro et al. (2012a) and was tested considering new small and short-term instances adapted from Costa (2005). we provide a summary of the total of the WRRSP studies discussed in this section in Fig. 17 in the Appendix.

4.4. Integrated problems

The interdependence of operations in the oil and gas sector requires that oil and gas companies plan and optimize their processes on an enterprise-wide level (Oliveira et al., 2013). As a result of the rig scheduling being a multifaceted decision process, many studies approach this problem by integrating this rig scheduling decision with others. We divide these studies into two classes of integration: field planning and resource planning.

4.4.1. Field planning

Before scheduling the rigs to drill new wells, field design and planning decisions are needed, such as well drilling schedule, well placement, facility design, and flow scheduling. Ideally, these problems should be solved together from a field planning perspective.

Using the Eclipse reservoir simulator and a polytope search optimization algorithm, de Andrade Filho (1994) addressed the drilling RSP deciding main development dates combined with the drilling rigs allocation and schedules. Since then, other studies also integrated reservoir simulator models with optimization algorithms, such as: linear programming and simulation approaches (Nesvold et al., 1996); a procedure for BP’s top-down reservoir modeling tool using an enhanced GA by Litvak et al. (2007), Litvak and Angert (2009) and Litvak et al. (2011); a GA (Litvak et al., 2007) with statistical proxies procedures using clustering-based techniques from Onwunalu et al. (2008); design space exploration (Cong et al., 2008); automated decision-making system with a first-in-first-out algorithm (Davidson et al., 2009); MINLP model and GA (Tavallali et al., 2015); approximation algorithms with optimization and local searches (Tavallali et al., 2016).

Several authors proposed formulations for field design and planning considering rigs. Iyer et al. (1998) proposed a multi-period MILP model with branch and bound to maximize the NPV. Currie, Novotnak, Aasboee, Kennedy, 1997, Currie, Novotnak, Aasboee, Kennedy, 1997 presented a simplified MIP model for the redevelopment and reservoir management of wells, deciding the projects, wells, and drilling rigs to be used annually. Van Den Heever, Grossmann, 2000, Van Den Heever, Grossmann, 2006 presented a MINLP model maximizing the NPV, which was solved using a dynamic programming (DP) approach with an iterative aggregation/disaggregation algorithm. Carvalho and Pinto (2006) proposed a model and a decomposition method to determine the drilling rigs (platforms) locations, the well to be drilled by each one, and the drilling schedule. Later, Barnes and Kokossis (2007) proposed mathematical models for an integrated field development when deciding the location, drilling schedule, and production rate of the wells. Similar models were also proposed by Wang et al. (2019) and Ondeck et al. (2019), but none of these previous studies considered the rig scheduling as a decision, but only as something that affects their decisions. Ondeck et al. (2019) performed a sensitivity analysis demonstrating the impact of the drilling rig fleet and crew mobilization costs in their model.

A system for field planning was presented by Martin et al. (2010), mainly for well design. The system designs the well-pad layout, determines the production facilities, allocates wells to rigs considering the fleet availability, rig locations, and other related attributes, and returns the rig schedule as one of its outputs. Omosebi et al. (2014) proposed a methodology based on project management to correctly plan drilling projects and rigs schedules. However, the authors did not mention the employment of optimization methods. Lange and Lin (2014) and Dewan et al. (2016) presented solutions that model the well scheduling process as a multi-agent system to allow optimal decisions, including the rig schedule, for all parts involved in the scheduling process. As mentioned by Neiro and Pinto (2004), this modeling strategy allows to integrate the business entities involved in the supply chain management. Kelly et al. (2017) introduced a MILP model for well startup considering each well as a batch process subject to resource availability constraints (processing plants, drilling rigs, and crew).

Also addressing the planning of an offshore oilfield infrastructure, Aseeri et al. (2004) proposed a sample average approximation (SAA) algorithm to maximize the NPV considering constraints of budget and the availability of one rig to drill the wells, optimizing the flow balance between production platforms, wells platforms, and the reservoirs. As showed by Smith (1956), rig availability constraints for the case of one rig can be considered as a RSP. The authors also considered the travel time between the wells when scheduling the rigs operations. Barnes and Kokossis (2007) introduced a MILP model for the analysis, design, and scheduling of offshore oilfields, considering the drilling schedule, platform locations, and a single rig available. Last, Calderón and Pekney (2020) focused on the field planning decisions related to the enhanced oil recovery to reduce gas flaring in shale oil development. The authors proposed a sophisticated model that optimizes drilling rig schedules, workover decisions, pipeline and facilities infrastructure, location of wells, and injection rates. A summary of the total of FP studies discussed in this section is illustrated in Fig. 18 in the Appendix.

4.4.2. Resources planning

The E&P operations need several resources, which are often planned separately. However, as their decisions might affect each other, resource usage should ideally be integrated with the E&P operations planning. This is the case for the rigs and the other resources involved in the E&P, such as crews and vessels. For instance, Hasle et al. (1996) used constraint reasoning for the well activity scheduling problem, where drilling rigs and wire-line cranes are appointed for drilling, completion, perforation, and logging activities. Horton and Dedigama (2006) presented a resource scheduling system used by an Australian oil company to schedule several operations, such as drilling, completion, and workover, and others that do not involve rigs, such as interconnections.

After completing an offshore well with a rig and before starting its production, offshore support vessels (OSV) are used to interconnect wells, manifolds, and platforms. Focusing on integrating the rig scheduling with the OSVs’ decisions, Accioly et al. (2002) used a constraint programming (CP) model to maximize oil production considering drilling, completion, workover, and pipelines connecting activities, priorities, precedence, wells, and ship characteristics. To enable the use of optimization solvers, the authors used different search heuristics to explore the solution space. Since then, several authors tested formulations and solution methods: CP model solved with hybrid TS algorithm (Nascimento, 2002); GRASP (Pereira, 2005, Pereira, Arnaldo, De Souza, 2005, Pereira, Moura, De Souza, 2005, Moura, Pereira, De Souza, 2008); GA (Vasconcellos and Ferreira Filho, 2006); CP model (Serra, Nishioka, Marcellino, 2011, Serra, 2012, Serra, Nishioka, Marcellino, 2012, Serra, Nishioka, Marcellino, 2012); continuous-time MILP formulation with upper bound relaxations (Serra et al., 2012c). Pereira (2005) and Pereira, Arnaldo, De Souza, 2005, Pereira, Moura, De Souza, 2005 formulated a CP model for scheduling drilling, completion, and interconnection operations in offshore wells with rigs, OSVs, and production units. The authors tested a GRASP to solve it in real instances of the Brazilian oil company Petrobras, which resulted in considerable savings for the company and, according to the authors, was implemented in a system called ORCA. Moura et al. (2008) adapted the formulation to consider resource displacement, proposing a GRASP to solve it. Based on the model proposed in Serra et al. (2011), Serra (2012), and Serra, Nishioka, Marcellino, 2012, Serra, Nishioka, Marcellino, 2012 proposed a CP model for offshore resource scheduling of a heterogeneous fleet of rigs and PLSVs, aiming to maximize production.

Others studies have tackled the RSP considering its equipment requirements. Drouven and Grossmann (2016) proposed a MINLP based on generalized disjunctive programming (GDP) for the shale gas development. The presented model maximizes the NPV defining which wells will be drilled, when they will be drilled, which rigs, crews, and equipment will perform the drilling, and the layout of the gathering pipelines. Mazzini et al. (2010) proposed a MILP model that decides rigs equipment and drilling/completion rigs schedules, minimizing the costs associated with resources contracts and rigs tardiness. Finally, Marchesi et al. (2019) proposed a MILP model for the construction of wells considering rigs and equipment aiming to minimize tardiness and earliness.

There are several types of workover operations and, as a result, different types of equipment are needed. With this assumption, McKechnie et al. (2002) presented a management system for workover operations that allows to control the rig schedule and the equipment needed. Later, a different problem was introduced by Pandolfi et al. (2010). The authors described a system called PAE (evolutionary algorithm for planning), applied in an extension of the WRRSP considering other resources such as crews and equipment used to service onshore wells. Later, Villagra et al. (2013) adapted the model proposed by Pandolfi et al. (2010) to consider penalty functions and repair algorithms to transform infeasible solutions into feasible ones in a constrained version of the problem. Achkar, Cafaro, Méndez, Cafaro, 2019, Achkar, Cafaro, Méndez, Cafaro, 2019 proposed a MILP model for this extended WRRSP, considering a heterogeneous rigs fleet, precedence constraints, crew shifts, and failure risks and minimizing production loss and costs. Finally, Aurachman et al. (2020) used an influence diagram analysis to model a variation of the WRRSP considering equipment decisions. According to the authors, they are developing a dynamic programming model in which the oil production loss changes with the waiting time.

The decision-making integrated with other resources is especially important for offshore P&A campaigns, which relies on rigs and lighter vessels, such as light well intervention vessels (LWIVs) and light construction vessels (LCVs). Bakker et al. (2017) approached the planning of the offshore P&A campaign, presenting a MILP model based on the VRP that aims to minimize costs of a heterogeneous fleet of semi-submersible rigs, mobile offshore drilling units, and light well intervention vessels. Adapting the model from Bakker et al. (2017), Bakker et al. (2019) developed a commodity flow type formulation for the P&A planning that allowed to tackle larger instances and consider different assumptions such as multiple routes per vessel and reduced operability of lighter vessels in the winter. Bakker et al. (2021) adapted these formulations to consider learning curve effects on the vessel’s processing times. All these P&A models were part of Bakker (2020), in which the author also presented a study problem using stochastic dual dynamic integer programming for the development of a mature offshore oilfield.

A summary of the total of RP studies discussed in this section is illustrated in Fig. 19 in the Appendix, together with further details on all of the literature presented.

5. Remarks, trends and opportunities

The papers found in the literature review were classified according to the taxonomy proposed in Section 2.2. These results are presented in the supplementary files and analyzed with data visualization tools in what follows. Fig. 7 contains the number of papers found for each taxonomy (rows) and classification group (columns), summarizing the answer for the second research question How the RSP has been most often addressed in the literature, both from academic and industrial perspectives?. Note that ”Scheduling” refers to problems that only consider scheduling, while ”Routing” refers to problems that consider routing integrated with scheduling.

Clearly, there is a pattern between the problem classification groups and the taxonomy. DRSPs tackle drilling/completion in stand-alone planning considering only the rigs. In some cases, they might consider other operations (workover or P&A) as well. Usually, the duration of the drilling operations is long and the distance (specifically the travel time) between wells is short. As a result, these studies are usually modeled as scheduling problems. The workover rig planning problems (WRSPs and WRRSPs) are also set in a stand-alone planning level considering only the rigs. However, differently from the DRSP, workover rig planning focuses on workover operations on the wells, usually considering single jobs representing interventions that are often unplanned and can be of much shorter duration than drilling operations. Therefore, the distance between the wells becomes a relevant aspect that is considered by modeling the problem as a routing problem (i.e., WRRSP). In addition, most workover problems consider a homogeneous fleet of rigs.

Field planning problems are those problems that tackle rig operations at an integrated planning level and are usually for drilling operations. Due to its complexity, most of these RSPs are modeled as scheduling problems and consider single jobs and homogeneous fleet. Resource planning problems are related to those RSPs that consider others resources when planning well operations (usually drilling or workover). As there are multiple types of resources, these problems consider multiple jobs per well and a heterogeneous fleet of rigs. Fig. 7 also reveals some literature gaps: few DRSPs modeled as routing problems; even fewer RSP considering P&A operations and workover rig planning problems for offshore wells; and a lack of field planning and resource planning for onshore oilfields or considering routing approaches.

5.1. Problem setting

Aiming to analyze the problem setting (oilfield and tasks type, planning level, resources considered, and study case presented) evolution, the studies were separated according to the publishing date in two groups: Before 2010 (orange bars) and 2010–2020 (blue bars). Fig. 8 contains the number of papers found in each group and problem characteristic.

In the past, the majority of studies were related to offshore wells, but the onshore problems have gained more attention in the last decade. Another notable point regarding the type of operations considered is that drilling RSP studies have decreased over the last decade. Meanwhile, the WRSP and WRRSP have increased considerably. However, the P&A field remains with few studies and it might be thus an important direction for future works.

We can observe that the number of studies using public data has increased significantly in the last decade. The majority of the research uses real or public data, which means that there are studies with a practical perspective fostering the exchange of knowledge between the academia and industry. Nonetheless, few studies were verified or implemented by companies, highlighting a gap in the literature. Futures work should therefore focus more closely on meeting the industry demands.

Furthermore, there was a decrease in integrated field development problems and an increase in stand-alone problems as the RSP gained priority in the decision-making. In contrast, we can observe a slight growth in studies considering other resources besides rigs, such as offshore support vessels (OSVs), lighters vessels, crews, equipment, and wire-line cranes, as shown in Fig. 9.

With the purpose of understanding more about the relationships underneath the problem characteristics, Fig. 10 presents a classification of the papers according to their oilfield, task types, and planning levels.

First, we observe in Fig. 10 that the problems considering P&A are more relevant for offshore wells and require an integrated field development perspective. Second, as mentioned by Tavallali et al. (2016), workover planning is a field operation (production phase) decision and is usually separated from field development. Therefore, studies addressing workover planning are usually stand-alone problems. Third, most of the attention of the workover problems has been to onshore wells, so there is an opportunity for WRSP and WRRSP for offshore oilfields. Last, we can observe that most of the drilling RSPs were for offshore wells and integrated field development.

According to Suslick et al. (2009), the offshore environment is immersed with uncertainties, high investments, and high-risk operations, which makes the offshore RSP more complex, requiring the drilling RSP to be treated as an integrated field development decision. Also, these results show new possibilities to studies related to applying an integrated field development for onshore wells and workover operations. Bissoli et al. (2016) suggested that in real situations, the WRSP and WRRSP models should consider all the possible elements that affect the optimization.

5.2. Approach

Aiming to observe the evolution of problem approaches (routing/scheduling, jobs, fleet type, and method) over time, the studies were separated according to the publishing date in two groups: Before 2010 (orange bars) and 2010–2020 (blue bars). Fig. 11 contains the number of papers found in each group and problem characteristic. The row R/S stands for Routing/Scheduling. Recall that the ”Scheduling” and ”Routing” taxonomies refer to problems that only consider scheduling and problems that consider routing with scheduling, respectively.

One can observe in Fig. 11 that there were some changes in the modeling approach over the last decade. Before 2010, most of the studies focused on scheduling, but since then, the number of studies incorporating routing has grown considerably and the scheduling-based approaches alone have fallen proportionally. A similar pattern is observed in the way that the jobs (operations) are modeled. Studies considering multiple jobs to be optimized have gained more attention. Meanwhile, single jobs have become less frequent. Finally, just as the previous attributes, the RSP considering a heterogeneous fleet has grown and was accountable for the majority of the studies in the last decade. In summary, there seems to be a trend towards turning modeling assumptions more realistic, and thus rig scheduling studies started to consider more complex assumptions, such as considering routing, multiple jobs, heterogeneous fleet, and other more realistic aspects, as mentioned by Santos (2018).

As to the solution methods (the approach row in Fig. 11), there was a reduction in the use of heuristics and metaheuristics, even though they still represent the most common type of method used. On the other hand, there was an increase in others approaches: exact (mathematical programming), matheuristic (hybrid methods combining heuristic and mathematical programming), simulation, simu-optimization (a hybrid approach combining simulation and optimization), and data-driven optimization (an emerging approach that uses machine learning methods applied to the optimization). This pattern follows Khor et al. (2017) literature review of the optimization methods used in field development problems, where sophisticated methods are being employed more often, in particular matheuristics and models that consider uncertainties in the costs, geological aspects, processing and traveling times, tasks occurrence, and rig availability.

We also highlight that a dynamic programming approach for the WRRSP (Silva and Silva, 2018) was found during our review. Bissoli et al. (2016) and Bassi et al. (2012) suggested, as future works, dynamic models allowing real-time optimization and rescheduling. Another crucial point is the employment of data-driven optimization (Ma, Vajargah, Lee, Kansao, Darabi, Castineira, 2018, Castiñeira, Toronyi, Saleri, 2018), which is a new trend in the areas of Operations Research and Management Science and entails using big data and machine learning (ML) techniques to devise improved models and/ or solution methods. Both authors focused on using ML to support the mathematical modeling, but there is the possibility of using the ML to improve the performance of the solution method as well. Next, Fig. 12 presents the number of publications found of each modeling approach (routing or scheduling), the task type studied (drilling/completion, P&A or workover), and the objective function used (time indicator, rig fleet size, oil production, oil production loss, costs, multi-objective or economic indicator).