Pressure gradient correlations analysis for liquid-liquid flow in horizontal pipes

1. Introduction

Liquid-liquid flow is defined as the simultaneous flow of two immiscible liquids in pipes (Atmaca et al., 2009). According to Park et al. (2016), this flow is frequently seen in different applications such as transport in the petroleum industry, emulsification and two-phase reactions and separation in process industries. However, the study of this flow system has been increasing with the years, as a consequence of its importance during oil extraction from oil wells. Usually during the process of extraction, a significant amount of water comes with the oil in pipelines or in some cases water is introduced for easier transportation (Izwan Ismail et al., 2015); this has important consequences in profit and it is specifically related with the changes in flow characteristics that are yet not fully understood.

Oil-water flow is characterized by large momentum transfer capacity, small buoyancy effects, low free energy at interface and small dispersed phase droplet size (Trallero et al., 1997). Since oil properties can be diverse, the viscosity ratio in this flow can vary on many orders of magnitude, but usually a low difference between densities is observed (Atmaca et al., 2009). In addition, the main difference between single phase flow and two phase flow is the presence of flow regimes (i.e. how the two phases are distributed), oil-water flow patterns are determined by different properties such as input flow velocities, how they are introduced, fluid properties, interfacial tension, pipe material (i.e. roughness), pipe inclination, among others (Ngan, 2010).

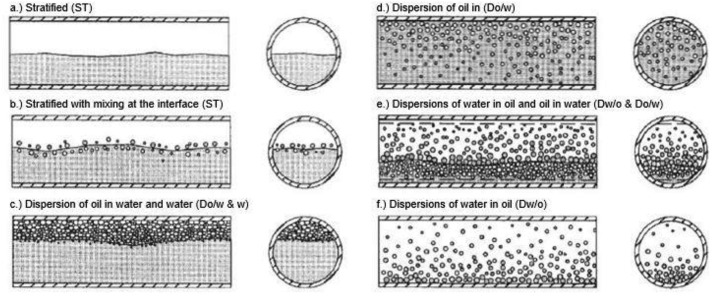
Flow patterns have been widely studied and authors have given them a huge number of different names. However, the most common flow patterns identified for horizontal flow are the ones specified by Trallero et al. (1997) and showed in Fig. 1.

When the superficial velocities of both, oil and water, are low, the flow is dominated by gravity and the phases are segregated with a smooth interface; this pattern is known as stratified flow (ST) (Fig. 1a) (Trallero et al., 1997). An increase in superficial velocities causes the appearance of interfacial waves with possible entrainment of drops at one side or both sides of the interface, leading to the stratified flow with mixture at the interface (ST&MI) (Fig. 1b) (Brauner, 2002). When the forces associated with the motion are not enough to maintain all the droplets suspended and some of them eventually settle a dispersion of oil in water and water (Do/w & w) (Fig. 1c) can be obtained. In addition, at sufficiently high water velocity, the entire oil phase becomes discontinuous in a continuous water phase resulting in an oil in water (Do/w) (Fig. 1d) emulsion; although, when the oil is the phase with high velocity the water phase is completely disperse in the oil phase resulting in a water in oil (Dw/o) (Fig. 1f) emulsion. These two emulsions may coexist obtaining a dispersion of water in oil and oil in water (Dw/o & Do/w) (Fig. 1e) (Brauner, 2002). These are the six flow patterns used in the present work.

Since each of the flow patterns named are the result of different flow characteristics, the understanding of the liquid-liquid behavior is essential in order to make a proper design of separation facilities, pumps, pipes and in general all methods related to oil extraction (Atmaca et al., 2009; Trallero et al., 1997). Through experimental studies, authors have determined how changes in the spatial distribution of the phases can have a significant impact on pressure drop; this makes determination of flow regimes and consequently, quantification of pressure drop across the pipe very important tasks.

Usually, flow pattern determination is made experimentally through visual observations and lastly, new equipment technologies have been also developed (Kee et al., 2014); in the case of pressure drop, it has been measured by experimental methods. Trying to make a non-experimental way of specifying these two factors, many authors created flow pattern maps based on their experimental studies and for pressure gradient, a few correlations have been developed according to flow pattern type.

In view of that, this paper presents a statistical analysis of correlations developed for the prediction of pressure gradient using experimental data from literature; in addition, for each model obtained after the statistical analysis, for semi dispersed and dispersed patterns, a non-linear fitting is made to improve its response.

2. Prediction of pressure gradient

As mentioned before, pressure gradient in pipes depends on flow patterns and flow rates; although some authors as Atmaca et al. (2009) and Sridhar et al. (2011), have stated that pressure drop is mainly influenced by oil viscosity (Izwan Ismail et al., 2015). In general, oil-water pressure drop has a greater magnitude than single-phase pressure gradient of water alone (Mukhaimer et al., 2015a, 2015b). Many authors have studied pressure gradient in horizontal and inclined pipelines with different conditions, fluids and experimental sections, and all have agreed that changes in pressure gradient are greatly related to the phase inversion phenomena and to flow pattern transitions (Izwan Ismail et al., 2015).

A few methods have been introduced in order to accurately predict pressure gradient; for some of them the results were satisfactory for certain flow pattern and failed to work with others. From stratified flow, dispersed flow to semi-dispersed flow has been studied. This is mainly because of the relation between pressure loss in an oil-water pipeline and the shear between the fluid and the pipe wall that is clearly affected by the distribution of the phases (Ngan, 2010; Trallero, 1995). Other elements that contribute to pressure gradient are pipe wettability and roughness, which means material of the pipe is also an important factor that must be taken into account. Pipe roughness restricts a liquid from moving smoothly and because of that, a pressure gradient is obtained during liquid-liquid flow (Izwan Ismail et al., 2015).

For the calculation of pressure gradient, many factors should be taken into account. Usually, densities, viscosities and velocities of the fluid are needed; a friction factor is also taken into account, which includes Reynolds numbers and pipe roughness. For some models, mixture viscosity is also another variable that must be calculated.

Friction factor correlations have been widely studied since 1840 with Hagen and Poiseuille (Assefa and Kaushal, 2015) and a great amount of modifications and new approximations have been presented. Similarly, for the calculation of mixture viscosity many correlations have been developed since Einstein's first equation in 1906 (Barnea and Mizrahi, 1973). A review of all of these equations can be found in Table A.1 and Table A.2 in Appendix A.

Moreover, a review of the pressure gradient prediction equations is presented in Table 1. As it can be seen, the friction factor correlations and in some cases the mixture viscosity calculation are needed. The statistical analysis made in the present work takes into account all possible combinations between the correlations without forgetting the principal objective: pressure gradient calculation.

Table 1. Pressure gradient existing correlations.

Author	Correlation	Developed for (Used for)
Arirachakaran et al. (1989)	$\frac{dp}{dz} = \frac{P_{o}}{P_{c}} {(\frac{dp}{dz})}_{fo} + \frac{P_{w}}{P_{c}} {(\frac{dp}{dz})}_{fw}$ (1) ${(\frac{dp}{dz})}_{f_{i}} = \frac{f_{i} ρ_{i} v_{i}^{2}}{2 g_{c} D}, i = {o, w}$ (2)	Stratified flow (ST, ST&MI)
Brauner (2002)	$\frac{dP}{dz} = 2 f_{m} \frac{ρ_{m} V_{m}^{2}}{D} - ρ_{m} gsinβ$ (3) $ρ_{m} = ρ_{d} ε_{d} + ρ_{c} (1 - ε_{d})$ (4) $V_{m} = V_{ds} + V_{cs}$ (5)	Dispersed flow (Do/w, Dw/o, Do/w & w, Dw/o & Do/w)
Elseth (2001)	$- A_{0} (\frac{dp}{dz}) - τ_{O} S_{O} + τ_{OW} S_{OW} + ρ_{O} A_{O} gsinθ = 0$ (6) $- A_{w} (\frac{dp}{dz}) - τ_{W} S_{W} - τ_{OW} S_{OW} + ρ_{W} A_{W} gsinθ = 0$ (7) $τ_{W} = 0.5 f_{W} ρ_{W} V_{SW}^{2}$ (8) $τ_{O} = 0.5 f_{O} ρ_{O} V_{SO}^{2}$ (9) $τ_{OW} = 0.5 f_{OW} ρ_{O} (V_{SO} - V_{SW}) \| V_{SO} - V_{SW} \|$ (10)	Stratified flow (ST, ST&MI)

In the Arirachakaran et al. (1989) model, used for stratified flows, the pressure gradient is calculated for each phase separately and a correlation is proposed. The assumptions used are: smooth interface, no relative motion, no mass transfer between the phases and no net shear force at interface (Arirachakaran et al., 1989). This is one of the first models developed for the calculation of pressure gradient for this kind of flow patterns and it was selected based on ws Ismail (2015) review article, where it is presented as one of the remarkable models used for stratified flows (Izwan Ismail et al., 2015).

For the dispersed flow the Brauner (2002) model is used; in this case the pressure gradient is calculated knowing that for fully developed flow the total pressure gradient is the sum of the frictional pressure gradient and the gravitational pressure gradient. It uses mixture properties, which implies the use of mixture viscosity correlations. This model neglects a possible difference between the in-situ velocities of the two liquid phases, which in one hand makes the calculation of the water holdup easier and on the other hand, is a strong assumption that is not valid for all the cases with dispersed patterns, especially the ones using low viscosity oils (Brauner, 2002). There are modifications of this model, which do not neglect the slippage between the phases, however, they are not used in this work since they are usually very complex models that depend mainly on the dispersed phase droplets size, value that is not presented in most experimental studies and is also really difficult to estimate in practice. However, according to Brauner (2002) the main issue of calculating the pressure gradient in liquid-liquid dispersed flow is the calculation of mixture viscosity, therefore the different correlations for the mixture viscosity are included in the present work.

In the last model, Elseth (2001) for stratified flow, the calculation of the pressure gradient is made based on a momentum balance for the oil and water phase; the holdup must be solved iteratively, and the interfacial shear stress is taken into account. The geometry plays a very important role in this model (Brauner, 2002; Elseth, 2001). It is important to mention, that although there are more complex models developed for the calculation of pressure gradient for these patterns the Elseth model was chosen because it has several advantages in comparison to the other ones. For example, the analytical solution presented by Brauner (2002) is for a specific range of conditions, i.e. fluid properties and velocities, contrary to the Elseth's model, which can handle different flow regimes in horizontal and inclined systems closer to reality. Another important factor is the computational effort needed for each model, which is less for Elseth model than for other complex analytical solutions, which require extensive computations (Brauner, 2002).

3. Dataset

The experimental dataset used, consists of 2132 registers from 27 experimental studies of different authors in horizontal pipes, as shown in Table 2. These authors used different fluids, superficial velocities, pipe lengths, diameters and materials.

Table 2. Experimental data used in the present study.

Author	Data	Fluids	Vsw[m/s]	Vso[m/s]	Volume ratio ( $ϕ_{W O}$ )	ε[m]	D [m]	L [m]	L/D
Abubakar et al. (2015)	86	Water-Mineral Oil (Shell Tellus S2 V15)	0.02–1.35	0.02–1.35	0.09–8.19	1.00E-04	0.0306	12	392.2
Al-Yaari et al. (2009)	85	Water-Kerosene (SAFRA D60)	0.1–2.78	0.1–2.79	0.25–3.93	1.00E-04	0.0254	10	393.7
Angeli and Hewitt (2000)	66	Water-Kerosene (EXXSOL D80)	0.11–2.65	0.43–2.65	0.06–5.98	1.00E-05 7.00E-05	0.024/0.0243	9.5/9.7	395.8/399.1
Castro et al. (2011)	6	Water-Oil	0.15	0.03–0.15	0.60–2.60	1.00E-07	0.026	12	461.5
Dasari et al. (2014)	68	Water - Lubricating Oil	0.19–1.06	0.11–1.19	0.20–4.40	1.00E-04	0.0254	1	39.4
Elseth (2001)	142	Water-Oil (Exxsol D-60)	0–2.48	0–2	0.05–25.82	4.50E-05	0.0563	10.2	181.3
Khatibi et al. (2015)	9	Tap water- Mineral Oil	0.02–0.7	0.01–0.9	0.10–5.02	5.00E-05	0.06	16	266.7
Kumara et al. (2009)	63	Water-Oil (EXXSOL D60)	0.001–1.46	0.001–1.46	0.02–32.42	4.60E-05	0.056	15	267.9
Kurban (1997)	75	Water-Oil (EXXSOL D80)	0.11–2.62	0.43–2.62	0.06–5.97	1.00E-04 4.50E-05	0.024/0.0243	9.5/9.7	395.8/399.1
Laflin and Oglesby (1976)	44	Water-N° 2 Diesel fuel	0.2–0.9	0.5–1.09	0.25–1.29	1.00E-04	0.0381	5.7	152
Liu et al. (2008)	41	Water-Diesel Oil	0.028–0.514	0.05–0.63	0.07–3.97	4.50E-05	0.026	11,1	429.4
Lovick and Angeli (2004)	86	Water-Oil (EXXSOL D140)	0.1–2.7	0.1–2.7	0.11–8.85	4.50E-05	0.038	8	210.5
Mukhaimer et al. (2015a, 2015b)	20	Water/Salty Water-Kerosene (Safrasol 80)	0.009–2.384	0.13–2.384	0.08–3.95	5.00E-06	0.0225	8	355.6
Nädler and Mewes (1997)	360	Water-Mineral Oil (Shell Ondina 17)	0.001–1.36	0–1.48	0.008–10.32	1.00E-04	0.059	48	813.6
Oglesby (1979)	236	Water-Oil	0.07–2.71	0.19–2.96	0.03–12.96	5.00E-05	0.0411	5.7	140.9
Rodriguez et al. (2011)	33	Water-Oil	1–3	0.2–1	1.02–14.82	1.00E-07	0.026	12	461.5
Schümann et al. (2016)	53	Tap Eater- Oil (Exxsol D80/Primol 352)	0.04–0.90	0.05–0.9	0.11–5.90	5.00E-06	0.1	25	250.0
Shi (2015)	15	Water- Oil (CYL 680/CYL 1000)	0.01–0.9	0.06–0.57	0.04–10.33	1.00E-04	0.026	1.7	66.5
Soleimani (1999)	95	Water-Oil (EXXSOL D80)	0.24–2.71	0.21–2.64	0.10–9.44	4.50E-05	0.0243	9.7	399.2
Souza and Rodriguez (2013)	115	Water-Heavy Oil	0.02–2.99	0.01–0.8	0.07–87.76	1.00E-07	0.026	6.1	234.6
Tan et al. (2015)	29	Water-Mineral White Oil	0.05–0.66	0.39–0.79	0.08–1.28	4.60E-05	0.05	2	40.0
Trallero (1995)	24	Water-Oil (Crystex Af-M)	0.01–1.82	0.01–1.59	0.006–133.77	1.00E-04	0.0501	15.5	310.2
Valencia (2003)	42	Tap Water-Oil (Purolube 150)	0.13–1.13	0.19–1.26	0.13–4.31	5.00E-06	0.253	4	16.0
Vielma et al. (2008)	90	Water-Refined Mineral Oil	0.02–1.80	0.05–1.75	0.01–32.25	1.00E-04	0.0508	21.1	415.9
Wang and Gong (2010)	85	Water-Mineral Oil	0.01–0.8	0.01–0.39	0.08–2.50	4.60E-05	0.0254	2	78.7
Yao et al. (2009)	53	Water-Crude Oil	0.05–0.792	0.068–0.901	0.23–1.72	4.60E-05	0.026	4	153.8
Yusuf et al. (2012)	111	Water-Mineral Oil	0.15–2.56	0.14–2.27	0.07–18.08	1.00E-04	0.0254	6.5	255.9
Total	2132

Since a variety of flow patterns names are found in literature, in order to homogenize the data and classify it in the six flow patterns already described, the tool developed by Urbano (2015) “The probabilistic flow pattern map generator” is used (Urbano, 2015). The distribution of experimental data over different parameters is shown in Fig. 2 and Table 3.

Table 3. Range of important parameters of database.

Parameter	Experimental
Parameter	Minimum	Maximum
Pipe inner diameter [m]	0.0225	0.253
Wall roughness [m]	1.00E-07	1.00E-04
Pipe length [m]	1	48
Length/Diameter [−]	16	813
Water superficial velocity [m/s]	9.98E-03	3.00
Oil superficial velocity [m/s]	1.06E-02	2.96
Water density [kg/m3]	983	1043
Oil density [kg/m3]	780	958
Water viscosity [Pa*s]	3.55E-04	1.00E-02
Oil viscosity [Pa*s]	1.57E-03	5.00
Tension [N/m]	0.0017	0.045
Volume ratio [−]	0.01	133.77

It is important to mention, that the initial database had 11106 registers for horizontal flow observations; however, just 2132 reported the experimental pressure gradient. In these terms, the use of OLGA Multiphase Toolkit 2014.3 was contemplated to complete the registers. In order to validate the results given by the software, it was decided to compare rigorously the experimental pressure gradient data that was reported with the one calculated through OLGA for the same registers. This was made for all data points, and also for each one of the flow patterns to find possible right predictions. The results were not satisfactory since high errors and lower R-squared values were obtained during the comparison, this can be seen in Fig. B.1, Appendix B. For this reason, it was decided to use only the registers that report experimental pressure gradient in order to minimize the effects over the results of the present study.

4. Methodology

The software used in this work is Matlab R2015a. One main code for pressure gradient analysis is made and has the following structure: data importation, data classification through flow pattern, calculations, statistics and results, as shown in Fig. 3.

The pressure gradient calculation part is divided by model. Each model has different inputs, which means not all the combinations of friction correlations, mixture viscosity correlations and pressure gradient models are evaluated. The number of combinations depend on the model definition. As an example, the Arirachakaran correlation calculates a friction factor for each one of the phases separately, which means no mixture viscosity correlation is used in that case. On the other hand, for Brauner correlation, mixture viscosity correlations are used as well as friction factor correlations, obtaining more different combinations to evaluate. Taking this into account, all possible combinations within these limitations are evaluated.

In the case of the non-linear fitting part, the software Matlab R2015a was again used, along with its function nlinfit. According to the results of the first part, a new model was proposed and through this tool the parameters of the regression were found. In this case, the new model was evaluated with using the same statistical parameters.

4.1. Statistics

Since the principal objective is to find the most practical, accurate and non-complex correlation combination, descriptive statistic and specific model comparison criteria are used. Here, the experimental data reported in the database and the one calculated for each pattern, as described before, are compared and analyzed (see Table 4).

Table 4. Statistical parameters used in the present work.

Statistical parameter	Equation
Average Percent Error (%) (E1) (Shoham, 2005)	$e_{i} = \frac{{dPdz}_{calc} - {dPdz}_{exp}}{{dPdz}_{exp}}$ (11) $E 1, % = \frac{1}{n} \sum_{i = 1}^{n} e_{i} * 100$ (12)
Absolute Average Percent Error (%) (E2) (Shoham, 2005)	$E 2, % = \frac{1}{n} \sum_{i = 1}^{n} \| e_{i} \| * 100$ (13)
Percent Standard Deviation (%) (E3) (Shoham, 2005)	$E 3, % = \sum_{i = 1}^{n} \sqrt{\frac{{(e_{i} * 100 - E_{1})}^{2}}{n - 1}}$ (14)
Average Error (Pa/m) (E4) (Shoham, 2005)	$e_{ii} = {dPdz}_{calc} - {dPdz}_{exp}$ (15) $E 4 = \frac{1}{n} \sum_{ii = 1}^{n} e_{ii}$ (16)
Absolute Average Error (Pa/m) (E5) (Shoham, 2005)	$E 5 = \frac{1}{n} \sum_{ii = 1}^{n} \| e_{ii} \|$ (17)
Standard Deviation (Pa/m) (E6) (Shoham, 2005)	$E 6 = \sum_{ii = 1}^{n} \sqrt{\frac{{(e_{ii} - E_{4})}^{2}}{n - 1}}$ (18)
Relative Performance Factor (−) (FRP) (Ansari et al., 1994)	$FRP = \sum_{i = 1}^{6} \frac{\| E_{i} \| - \| E_{i, min} \|}{\| E_{i, max} \| - \| E_{i, min} \|}$ (19)
R-squared (R2) (Samadianfard, 2015)	$a = \sum_{i = 1}^{n} {dPdz}_{exp} {dPdz}_{calc}$ (20) $b = \frac{1}{n} \sum_{i = 1}^{n} {dPdz}_{exp} \sum_{i = 1}^{n} {dPdz}_{calc}$ (21) $c = \sum_{i = 1}^{n} {dPdz}_{exp}^{2} - \frac{1}{n} {(\sum_{i = 1}^{n} {dPdz}_{exp})}^{2}$ (22) $d = \sum_{i = 1}^{n} {dPdz}_{calc}^{2} - \frac{1}{n} {(\sum_{i = 1}^{n} {dPdz}_{calc})}^{2}$ (23) $R^{2} = \frac{{(a - b)}^{2}}{(cd)}$ (24)
Akaike Information Criterion (AIC) (Assefa and Kaushal, 2015)	$AIC = n \ln (\sum_{i = 0}^{n} e_{ii}^{2}) + 2 K$ (25)

The average percentage error (E1) and the average error (E4) indicate the agreement between calculated and measured data. Positive values imply overprediction and negative values underprediction. The absolute average percentage error (E2) and the absolute average error (E5), represent the general percentage error of the calculations. The percent standard deviation (E3) and standard deviation (E6) indicate the scatter of the error in respect to their corresponding average error. The three first terms are based on percentage error rather than relative pressure error, which means relative small pressure error that experience a small pressure gradient may give a large percentage error even though the pressure error itself is not that far from the actual measurements. In order to make the statistics independent of the magnitude of pressure gradient the other three identical statistical parameters are defined (Shoham, 2005; Ansari et al., 1994).

In addition, the relative performance factor (FRP) created by Ansari et al. (1994)(Ansari et al., 1994) is a composite error factor with descriptive statistic criteria in it. The minimum and maximum possible values of FRP are 0 and 6, corresponding to the best and worst prediction performance. The value of R-squared is a statistical measure of how close the data are to the real values and in general, the higher the value, the better the model fits the data. On the other hand, the Akaike Information Criterion for a given data set has no meaning by itself, although the value can be interpreted if it is compared with the AICs of a series of models based on the same data set (observations) with the same dependent variables. Since this criterion takes into account the variables used by the model, a complexity comparison is being made, the lower the AIC most appropriate the model (Burnham and Anderson, 2002).

5. Results and analysis

In this section results are presented in order. First pressure gradient model analysis, followed by non-linear fittings results.

5.1. Statistical analysis

Since each pressure gradient model was defined for a specific flow pattern, only the possible combinations within these models are evaluated. Since statistical analysis was made to evaluate the performance of each combination, trying to find the most practical, accurate and non-complex model, only the five best combinations with their statistics and graphical results are presented.

5.1.1. Stratified flow (ST)

For this pattern, 64 possible combinations were found to be valid for the 229 experimental data points. The graphical and statistical results of the best five combinations are presented in Table 5 and Fig. 4.

Table 5. Statistical results for ST.

Pressure Gradient Model	Friction Factor Correlation	E1 (%)	E2 (%)	E3 (%)	E4 (Pa/m)	E5 (Pa/m)	E6 (Pa/m)	FRP	R2	AIC
Elseth (2001) (Eq. 6)	Drew et al. (1936) (Eq. 36)	−68.96	69.53	378.64	−2246.02	2246.40	51167.84	1.36	0.09	5274.56
Elseth (2001) (Eq. 6)	Eck (1973) (Eq. 39)	12.31	86.30	1315.27	−2143.71	2201.96	50661.56	0.83	0.21	5266.87
Elseth (2001) (Eq. 6)	Round (1980) (Eq. 47)	12.28	86.36	1315.94	−2142.89	2201.16	50667.31	0.83	0.21	5266.87
Elseth (2001) (Eq. 6)	Haaland (1983) (Eq. 52)	12.27	86.36	1315.98	−2142.92	2201.18	50667.59	0.83	0.21	5266.87
Elseth (2001) (Eq. 6)	Shaikh et al. (2015) (Eq. 90)	−1.06	86.18	1303.64	−2162.57	2216.18	50591.54	0.72	0.22	5267.10

As it can be seen, the average error is between 69 and 87% for combinations using Elseth (2001) model. It can be seen that no combination uses the Arirachakaran model, for the reason that the main difference between these two models is that the first one takes into account the interfacial shear stress between the phases, while the second one is a correlation that calculates pressure gradient for each phase separately. The standard percent deviation and average error of the first combination are lower than the ones for all the other combinations. However, the R-squared and the AIC showed that it may not be the best option in terms of complexity and dispersion of data.

The graphical results confirm the underestimation of the pressure gradient in the first case agreeing to the statistical results presented. In addition, a very similar behavior between the other options can be seen. It is important to mention, that this pattern is not characterized by a higher-pressure gradient, which affects the calculation of a few combinations due to the fact, that some friction factor correlations were developed specifically for turbulent flow, i.e. higher Reynolds numbers. In addition, this pattern was defined as with a smooth interface which agreed with the assumptions made by the Elseth (2001)model. The error encountered for the first combination, is still significant, but it represents a good first approach to the calculation of pressure gradient for stratified flow regimes.

5.1.2. Stratified flow with mixture at the interface (ST&MI)

For this pattern 493 experimental data points, 62 possible combinations were evaluated using the two models for stratified flow. The summary of the results of the best five combinations can be seen in Table 6 and Fig. 5.

Table 6. Statistical results for ST&MI.

Pressure Gradient Model	Friction Factor Correlation	E1 (%)	E2 (%)	E3 (%)	E4 (Pa/m)	E5 (Pa/m)	E6 (Pa/m)	FRP*10−4	R2	AIC
Elseth (2001) (Eq. 6)	Colebrook (1939) (Eq. 32)	−53.17	60.15	704.21	−2477.03	2494.82	82759.45	1.93	0.01	11722.40
Elseth (2001) (Eq. 6)	Brkic a (2011) (Eq. 85)	−52.52	60.23	711.59	−2474.39	2496.38	82839.42	2.00	0.01	11718.51
Elseth (2001) (Eq. 6)	Tsal (1989) (Eq. 57)	−54.59	60.27	685.26	−2493.17	2504.91	82728.58	2.09	0.02	11719.07
Elseth (2001) (Eq. 6)	Moody (1947) (Eq. 34)	−53.83	60.31	698.31	−2485.64	2500.92	82745.17	2.03	0.01	11718.67
Elseth (2001) (Eq. 6)	Avci and Karagoz (2009) (Eq. 78)	−52.41	60.33	714.77	−2474.33	2496.45	82839.04	2.01	0.01	11718.50