A new four-dimensional chaotic attractor

1. Introduction

Chaotic systems are nonlinear systems which are sensitive to initial conditions and exhibit rich dynamic behavior [1]. Furthermore, a chaotic attractor is defined as a chaotic set toward which a dynamic system tends to evolve [2]. Chaotic systems have wide range of applications in many Engineering and non-Engineering fields, some of their applications are found in intelligent controls [3], power systems [4], secure communication [5], biology [6], and mathematics [7].

Furthermore, chaotic attractors were discovered by Lorenz while he was studying atmospheric convection, then, he introduced the first three-dimensional chaotic system in 1963 [8]. Afterwards, Rossler continued this work of dissipative dynamical system and proposed a new chaotic system in 1976 [9]. More work has been conducted since then, for example Chen introduced a new three-dimensional attractor in 1999 which is not topologically equivalent to Lorenz system [10]. In addition, recently there has been great interest in investigating hidden attractors where basin of attraction does not intersect with small neighborhood of equilibria [11], [12], [13], [14], [15].

Proposing of new chaotic attractors with new structures and dynamics is very useful to the field of chaos theory and its applications [3], [4], [5], [6], [7]. In this paper, a new four-dimensional chaotic system is introduced; it is mainly consist of four multiplier terms and four simple terms. The contribution of this work is that it proposes a novel system which has different structure and topology of existing four-dimensional systems [16], [17], [18]. The fundamental characteristics of the new system are investigated by means of equilibrium points, their stabilities, bifurcation diagrams, Poincare maps, and power spectrum. Further investigations of the system are conducted in next section. However, the system is completely new and does not belong to a known family of known systems.

The rest of paper is organized as follows. In Section 2, the new four-dimensional chaotic system is presented. In Section 3, the numerical analysis and simulation of system dynamics are shown. In Section 4, an optimal controller design based on Riccati equation is derived and implemented. Finally, conclusions are presented in Section 5.

2. The new four dimensional chaotic system

The new chaotic system has the following set of four dynamic equations:(1) $\begin{matrix} \dot{w} = a (x - w) \\ \dot{x} = b w - wy \\ \dot{y} = wx - xz \\ \dot{z} = xy - y \end{matrix}$ where $x = {[w, x, y, z]}^{T}$ is the state vector of the system. The significance of the system in (1) is that it presents a new 4D chaotic system with a different dynamics than existing systems. To study the system we first look at the equilibrium points which are found by setting Eq. (1) to zero. This produces two equilibrium points: (0, 0, 0, 0) and (1, 1, b, 1). In order to study their stabilities the Jacobian of (1) is found as follows:(2) $J = [\begin{matrix} - a & a & 0 & 0 \\ b - y & 0 & - w & 0 \\ x & w - z & 0 & - x \\ 0 & y & x - 1 & 0 \end{matrix}]$

The linearized system at first equilibrium point (0, 0, 0, 0) is given by the following Jacobian matrix:(3) $J = [\begin{matrix} - a & a & 0 & 0 \\ b & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & - 1 & 0 \end{matrix}]$

The characteristics equation for (0, 0, 0, 0) is $λ^{2} (λ^{2} + a λ - ab)$ and the roots are given as double poles at origin and the other poles at $\frac{- a \pm \sqrt{a^{2} + 4 ab}}{2}$ which makes the point is unstable point.

The linearized system at second equilibrium points (1, 1, b, 1) is given by the following Jacobian matrix:(4) $J = [\begin{matrix} - a & a & 0 & 0 \\ 0 & 0 & - 1 & 0 \\ 1 & 0 & 0 & - 1 \\ 0 & b & 0 & 0 \end{matrix}]$

Moreover, The characteristics equation for the point is $λ^{4} + a λ^{3} + (a - b) λ - ab$ and applying Routh-Hurwitz criterion yields that this point is $V (t) = V (0) e^{- at}$ stable only for $a > 0$ and $ab < 0$ .

The new system is proved to be dissipative system for all positive $a$ since the divergence of flow of the system is:(5) $\frac{1}{V} \frac{dV}{dt} = divV = \frac{\partial \dot{w}}{\partial w} + \frac{\partial \dot{x}}{\partial x} + \frac{\partial \dot{y}}{\partial y} + \frac{\partial \dot{z}}{\partial z} = - a$

And $V (t) = V (0) e^{- at}$ with rate of contraction $\frac{dV}{dt} = V (0) e^{- a}$ . Eq. (5) proves the existence of a bounded and attracting chaotic set that form the attractor.

3. Numerical analysis

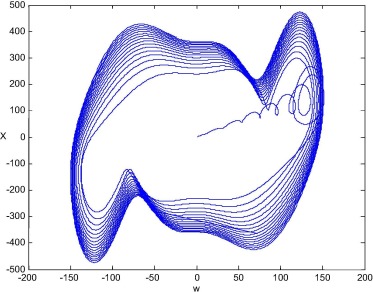
The new chaotic system has been tested for a wide range of parameter values and proved to yield chaotic behavior for many selections of parameters $a$ and $b$ . By choosing one pair values as $a = 23$ and $b = 9$ the chaotic system in (1) is dissipative and the two equilibrium points are unstable. The portrait for two dimensions and three dimensions, for initial conditions (1, 1, 1, 1), are shown below. First, the phase-plane for x-w is shown in Fig. 1, and the phase-plane for y-z is shown in Fig. 2.

Then, the 3D portraits are shown in Fig. 3, Fig. 4, Fig. 5, for different arrangements of the axes.

The power spectrum of signal describes how the variance of the data is distributed over the frequency domain [19]. Fig. 6 shows the power spectrum of the signal w(t) of the system (1). It is obvious from the figure that the system has a bandwidth of roughly 0–50 Hz.

Based on the algorithm presented [20] by Alan Wolf, the Lyapunov exponentsare calculated using Matlab with step-size 0.05 and after 10,000 iterations as follows:

LE1 = 1.86137, LE2 = −2.95652, LE3 = −3.88644, LE4 = −18.0247 and Lyapunov dimension of 1.6296.

Moreover, bifurcation diagram displays the maxima and peaks of numerically computed solutions of a system as a function of a bifurcation parameter in the system while other parameters are fixed [21]. The chaotic dynamic of the system as a function of parameter a, and b = 9, is displayed in Fig. 7 and shows a stable system when parameter a is less than 8 and chaotic system when it is greater than 8.

Furthermore, the chaotic dynamic of the system as a function of parameter b, and a = 23, is displayed in Fig. 8, and shows a stable system when parameter b is less than 7.5 and chaotic system when it is greater than 7.5. Furthermore, a closer look at the system trajectories would place it as hidden attactor.

Another way to look at the system dynamics is through Poincaré maps of the system, which is a technique that represents the phase space of the system by isolating some trajectories [22]. Fig. 9, Fig. 10, Fig. 11, Fig. 12, Fig. 13, Fig. 14show the Poincaré maps in different 2D planes while other two variables are set to zeros. It is noticed that several planes of the system are symmetrical. For example, both planes in Fig. 10 shows even symmetry around the y-axis, while Figs. 11(a) and 13(a) show odd function curves. In addition, Fig. 14 shows even symmetry function curves around the z-axis. Note that the range of coordinates is in magnitude of hundreds, therefore the other variables are set to |variable| < 5 rather = 0 to compensate for numerical approximations.

4. Optimal control design

Linear Quadratic Regulator (LQR) is a popular case of optimal control where a measure of the quadratic continuous time cost function(6) $J = \frac{1}{2} \int_{0}^{\infty} [X^{T} (t) Q (t) X (t) + u^{T} (t) R (t) u (t)] dt$ is minimized. And it is subjected to linear dynamic constraints as given in the linearzed Jacobian system discussed in Section 2. Both Q and R matrices are positive definite matrices to ensure the cost measure remain positive. Furthermore, the negative feedback controller, shown in Fig. 15, is in the form(7) $u (t) = - Kx (t)$

It has been shown in optimal control theory that the feedback controller $K$ is given by $K = R^{- 1} B^{T} S$ where S is the solution of the well known Algebraic Riccati equation (6)(8) $A^{T} S + SA - {SBR}^{- 1} B^{T} S + Q = 0$ where S is symmetrical solution matrix [23]. This controller is calculated around every point of the trajectory. Fig. 16, Fig. 17 show the four trajectories with the controller is applied after 3 s to drive the trajectories to the origin.