From fundamentals to implementation of yield stress for nautical bottom: Case study of the Port of Hamburg

1. Introduction

Suspended matter is distributed in the water of rivers, lakes and coastal waters. It consists of organic and inorganic components. Due to their small particle size, the inorganic components remain in suspension despite their significantly higher density compared to water. These clay minerals have a layer charge and therefore have electrostatic forces of attraction on positively charged particles. Organic components have densities like water and are therefore in suspension. Organic components always have functional groups which are not electrically neutral. Depending on the type of functional groups, there are positive and negative charges. When differently charged particles come very close to each other, they attract and combine to form larger structures called flocs. The bonds are of different types such as dipoles and hydrogen bonds. The flocs then consist of organic matter with embedded mineral particles.

Mechanical forces can break down larger flocs into smaller flocs. Flow turbulence thus controls the size of the flocs. In zones with calmer currents, the growth of larger flocs is particularly favored. With increasing floc size, the settling velocity increases, so that the sedimentation of the suspended matter flocs occurs in those areas. During sedimentation process, these suspended matter flocs accumulate near the bottom, where turbulence decreases. This process promotes the formation of even larger flocs. However, higher floc concentrations can impede sedimentation process. Sometimes a transition area forms in which flocs can no longer move independently of each other. This transition layer is structurally a fluid, but distinct from rheological perspective, from the water above, along with higher densities. These transition layers are typically referred to as “fluid mud” (Kineke et al., 1996; Mehta, 1991). With increasing depth, further consolidation occurs. They no longer consist of individual flocs, but form a large network of water, clay minerals, sand, silt and organic substances (such as living microorganisms and in particular their excreted biopolymers) (Mehta, 2013). The presence of these larger network structures of mud can be observed particularly well in erosion tests (Zhang et al., 2018). In the field of marine geology, fluid mud layer is typically referred to as a fluffy layer (Zhang et al. 2021, 2022), puff layer (Brun-Cottan et al., 2000) or wave-supported mud layer (Hooshmand et al., 2015; Wen et al., 2020).

In fluid mud, solid particles are no longer suspended in the mud layers. The water is then stored between greater network structures. These mud layers are typically subject to continuous wave motion and disturbances caused by ship motion (Mehta, 2013; Ross and Mehta, 1989), human intervention such as dredging (Gordon, 1974), natural climate events, and bioturbation (Harrison and Wass, 1965). Water body of a river, coastal water or lake in calmed areas can be divided into different layers from top to bottom:

•
Water body contains suspended matter (SPM), (No impairment of shipping)
•
Solid suspension close to the ground with predominantly fluid properties (fluid mud (FM)) but it differs significantly from the SPM areas in terms of density and rheology, (this layer can be made accessible to shipping)
•
Pre-consolidated sediment (PS), (Not navigable! possibly tolerable at moorings)
•
Consolidated sediment (CS), (Not navigable! If CS is above the target depth, it must be dredged) (Shakeel et al., 2020d)

The near-bottom fluid mud layer is exposed to strong local fluctuations. In some places it can be several meters thick, in other places it is completely absent. Fluid mud, the most important mud layer from a navigational perspective, is typically identified as a layer with a density of 1030–1300 kg. m−3 whereby hindered settling of particles plays a role due to the presence of the described flocs (Inglis and Allen, 1957; McAnally et al., 2007; Whitehouse et al., 2000). All mud layers, but particularly the fluid mud layer, display complex rheological behavior, i.e., combination of thixotropy, shear-thinning, two-step yielding and viscoelasticity (Coussot, 1997; Van Kessel and Blom, 1998). The rheological/cohesive properties of mud are observed to vary as a function of solid fraction (or bulk density), type and concentration of organic matter, type of clay minerals and ionic concentration (Malarkey et al., 2015; Parsons et al., 2016; Paterson et al., 1990; Paterson and Hagerthey, 2001; Schindler et al., 2015; Shakeel et al., 2019a, 2020d; Wurpts and Torn, 2005). The thorough understanding of the rheological characteristics of mud, as a function of above-mentioned parameters, needs to be performed to estimate the strength, the flow and thickness of (fluid) mud in ports and waterways. The quantification of the rheological properties for fluid mud also facilitates the definition of boundary conditions for sediment transport modelling, which in turn helps optimizing the dredging operations and defining the proper maintenance strategy for navigational channels (Kirichek et al., 2018, May, 1973, Parker and Kirby, 1982, Richard Whitehouse et al., 2000). However, in order to calibrate and improve the in-situ measurement techniques, it is essential that the key rheological parameters are extensively estimated beforehand in the laboratory using suitable protocols.

First of all, in this review paper, nautical bottom concept is explained from rheological point of view in section 2. In the next section, different rheological protocols used to measure the yield stresses of mud are detailed and compared. Furthermore, the two-step yielding behavior of mud is described from microstructural point of view followed by the presentation of semi-empirical model used to capture that two-step yielding behavior. The influence of different factors such as density, organic matter content, dilution, organic matter degradation, salinity and temperature on the rheological behavior of mud is discussed in Section 3. In the end, the nautical bottom is defined on the basis of rheological properties of mud for Port of Hamburg as a case study.

2. Defining nautical bottom based on rheology

Safe navigation and excellent accessibility within ports and waterways is vital for port authorities. Safe navigation is primarily controlled by the space available under the ship's keel, referred to as under keel clearance (UKC). There are two approaches for maintaining a sufficient UKC: (i) by restricting the maximum draft of vessels, and (ii) by controlling the desired nautical bottom with dredging operations (Kirichek et al., 2018). The nautical bottom is typically defined as: “a level at which physical characteristics of the bottom reach a critical limit beyond which contact with a ship's keel causes either damage or unacceptable effects on controllability and manoeuvrability” (PIANC, 1997).

The first approach is uneconomical because it would restrict the accessibility of the port for larger and energy efficient vessels. The second option is more favourable for port authorities, however, the environmental impact and cost of the dredging operations can limit its applicability. The nautical bottom definition provides a general viewpoint without giving a practical solution. Moreover, this definition raises a number of questions including:

1.
How to define and quantify “unacceptable effects”?
2.
Which physical parameter(s) are associated to the “characteristics of the bottom”?
3.
How to define and estimate critical value(s) of this/these parameter(s)?

The answer to the first question depends on several parameters such as training and expertise level of pilots, local environmental conditions, size and speed of the vessel, quality of navigational assistances (availability of tug assistance) and influence of the fluid mud on the manoeuvrability of the vessels. For the other two questions, the selected physical characteristics should directly relate to the forces exerted by the mud layer on the ship's hull upon its contact.

Two different approaches are typically used to maintain the desired nautical bottom: (i) passive approach (McAnally et al., 2016) and (ii) active approach (Wurpts and Torn, 2005). Passive approach relies on a bathymetric surveymethod which ultimately leads to the recommendation of a mud property beyond which it is safe/unsafe for a ship to sail. This mud property is typically the bulk density for most cases. For example, the ports of Rotterdam, Suriname, Bangkok, Bordeaux, and Nantes adopted a density criterion of 1200 kg. m−3(McAnally et al., 2016). Bottom surveying techniques such as echo-sounding are generally used to detect the mud-water level. However, the frequency dependence of echo-sounding results is the most common problem with this technique, and a proper calibration is difficult owing to the variability in mud composition (Vantorre et al., 2006). On the other hand, active approach relies on the maintenance of navigational channels whereby the physical, biological and chemical properties of fluid mud are tuned in order to significantly influence its rheological and settling behaviour. This methodology has been adopted in the Port of Emden. The mechanical destruction of the mud's floc structure restricts the rapid consolidation of mud (McAnally et al., 2016).

As navigability is strongly linked to the flow properties of the water-mud medium, rheological properties like viscosity and yield stress (i.e., stress required to initiate the flow of mud) are better candidates to define suitable physical characteristics and can be utilized to define a suitable criterion. The reason for selecting bulk density as a criterion for nautical bottom is linked to the limitations of in-situ measurements of rheological properties and the lack of systematic investigation of rheological characteristics of mud. However, recent developments made it possible to effectively analyse the in-situ rheological properties of mud (Kirichek and Rutgers, 2020). On the other hand, German ports like the Port of Emden defined the nautical bottom on the basis of yield stress of mud (50–100 Pa) (Wurpts and Torn, 2005) with the corresponding density values ranging from 1100 to 1250 kg. m−3 (Uliczka, 2005). This variation in density values is linked to the fact that the relation between density and yield stress can be significantly influenced by several parameters including type and content of organic matter, clay type, particle size distribution and salinity. Hence, it is difficult and impractical to choose a critical value of the density for a port with varying above-mentioned parameters along the port. In short, for defining nautical bottom based on rheological properties of mud, the following points need to be considered: (i) systematic analysis of the influence of different parameters (TOC content, type and state of organic matter, bulk density and salinity) on the rheology of mud, (ii) appropriate tools for in-situmeasurement of rheological properties, and (iii) proper correlation between lab and in-situ measurements.

3. Yield stress

Bingham and co-workers introduced the term yield stress for plastic yielding in metals (Barnes, 1999; Bingham, 1922). The estimation of yield stress is vital for various industrial processes particularly for defining nautical bottom for ports and waterways (Kirichek et al., 2018; Møller et al., 2006; Nguyen and Boger, 1992). In addition to the yield stress, other rheological properties of mud are also important particularly the viscosity, moduli and shear rate. High shear rateviscosity (i.e., infinite viscosity) is typically used in sediment transportmodelling along with the yield stress of sediments. However, in this review paper, only yield stress is considered and explained because this rheological property is used in literature for defining nautical bottom (Wurpts and Torn, 2005).

3.1. Rheological protocol

Several experimental techniques and protocols have been developed, in the past two decades, to estimate the yield stress of soft materials. However, the yield stress values obtained from these protocols/techniques may vary depending upon the handling procedure of sample and selected method (James et al., 1987; Nguyen et al., 2006; Steffe, 1996; Uhlherr et al., 2005; Zhu et al., 2001), which is attributed to the differences in criterion of yield stress definition, principle and time scale associated with the chosen methodology (Cheng, 1986).

There are several conventional methods to measure yield stresses such as steady ramp-up (based on stress or shear rate), oscillatory sweep (based on stress or strain), stress growth (at constant shear rate) and creep (at constant shear stress) (Coussot, 2014; Dinkgreve et al., 2016; Nguyen and Boger, 1992). In addition to these methods, some protocols are specially designed for estimating the yield stresses of mud samples. For example, Claeys et al., (2015) developed a protocol to measure the yield stresses (in terms of undrained shear strength and dynamic yield stress) of mud by obtaining an equilibrium flow curve using vane geometry. This protocol starts with the application of a lower shear rate (1 s−1), which gives the undrained shear strength of mud, followed by the application of nine or more shearing cycles (15–20 min) at required shear rates with intermittent shearing at 1000 s−1, to completely destroy the structure and to obtain the reproducible state. The resultant equilibrium flow curve gives the dynamic yield stress at lower shear rates. This protocol is not very suitable to estimate the yield stresses of a large number of samples. Moreover, the use of vane geometries in fluid sediment samples should be assessed critically, because of the secondary flows particularly at higher shear rates.

Different rheological geometries are available to perform rheological experiments including concentric cylinder, cone and plate, parallel plate and vane. However, each geometry has its own benefits and limitations and is typically selected on the basis of nature/composition of sample. In literature, the rheological properties of mud samples from different sources have been extensively investigated by using different geometries and rheological methods (Babatope et al., 2008; Bai et al., 2002; Coussot, 1997, 2007; Fass and Wartel, 2006; Huang and Aode, 2009; Jiang and Mehta, 1995; Van Kessel and Blom, 1998). For instance, Van Kessel and Blom (1998) presented a comparative analysis of rheological properties of natural and artificial mud samples using three different geometries: (i) Couette, (ii) double concentric and (iii) cone and plate. The results showed that the yield stress values were dependent on the geometries.

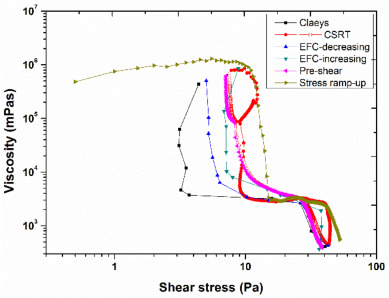
Moreover, the comparison of different protocols in terms of apparent viscosityas a function of shear stress for mud samples from Port of Hamburg is shown in Fig. 1. Two yield stresses (static and fluidic) extracted from the two viscosity declines are presented in Table 1. The higher yield stresses are obtained by using shear rate ramp-up step of CSRT test, increasing equilibrium flow curve (EFC) test and stress ramp-up test, which is associated to the fact these protocols destroy the mud samples from an undisturbed state. Therefore, these protocols are suitable to estimate the yield stresses of mud samples which are present in undisturbed or unremoulded state (or fast recovery after disturbance) under in-situ conditions. Moreover, the stress ramp-up test is fastest and more reliable to measure yield stresses of large number of mud samples. The remaining protocols (decreasing equilibrium flow curve, ramp-down step of CSRT, pre-shear and Claeys et al.) give lower yield stress values, which verifies the extensive structural breakdown of samples during measurement. These protocols are, however, useful to measure the yield stresses of mud samples which exist in disturbed state (remoulded state) under in-situ conditions. This analysis also highlights that the yield stresses of both remoulded and unremoulded sample can be obtained by performing a shear rate ramp-up and ramp-down test (CSRT) along with some information about the thixotropic or time-dependent behaviour of mud.

Table 1. Static and fluidic yield stress values of mud sample from port of Hamburg obtained from viscosity declines with Couette geometry for different protocols (Shakeel et al., 2021b).

Method	Static Yield Stress (Pa)	Fluidic Yield Stress (Pa)
Claeys et al.	3.1–4.4	26
CSRT-ramp up	9.0–12.3	40
CSRT-ramp down	7.6	29
EFC-decreasing	5.2	26
EFC-increasing	7.1	38
Pre-shear	7.1	27
Stress ramp-up	11	40

3.2. Two-step yielding

In addition to the single-step yielding, a prominent two-step yielding behaviour was found for different soft materials such as carbopol microgel (Shao et al., 2013), colloidal glasses (Pham et al., 2008), colloidal gel (Chan and Mohraz, 2012), muscovite dispersions (Nosrati et al., 2011) and magneto-rheological systems (Segovia-Gutiérrez et al., 2012). This two-step yielding behaviour is either linked to the wall slip artefact (Barnes, 1995), which can be easily checked by performing experiments with different gaps or with roughened geometries (Shakeel et al., 2020b), or attributed to the material's response due to the existence of different structural levels/structural (re)organizations (Ahuja et al., 2020). Oscillatory amplitude sweep test is typically performed to analyse the two-step yielding behaviour of a sample by recording the moduli ( $G^{'}$ and $G^{″}$ ) as a function of applied oscillatory stress or strain. The storage ( $G^{'}$ ) and loss ( $G^{″}$ ) moduli are the in-phase and out-of-phase responses of the material, respectively, to the applied sinusoidal stress/strain. The two-step yielding response is identified by the two declines in the moduli, which are typically associated to the bond and cage breaking process (Dagois-Bohy et al., 2017). Moreover, it is important to note that at higher amplitudes it is difficult to define $G^{'}$ and $G^{″}$ in a conventional way due to the presence of higher harmonics and, therefore, it is useful to analyse the data in terms of Lissajous plots.

Nie et al., (2020) reported the two-step yielding behaviour of mud by using both steady and oscillatory tests. The authors attributed the first yield point to the breakup of particle network structure while the second yield stress was linked to the complete breakup of aggregates. After the second yield point, the aggregates/flocs became individual particles and the mud sample behave like a viscous fluid. A similar two-step yielding behaviour was observed for mud samples by plotting the data in terms of viscosity as a function of shear stress obtained from different creep tests (Mehta et al., 2014). The origin of this two-step yielding behaviour in mud was also investigated by using a parallel plate shearing device with an upright microscope (RheOptiCAD® (Shakeel et al., 2019b),). The results showed that the first yield point was linked to the breakage of interconnected network of flocs, followed by the formation of hollow cylinder-like structures which provided the second plateau in moduli or viscosity. The second yield stress was associated to the collapse of these reorganized cylinder-like structures into smaller flocs or aggregates, see Fig. 2(Shakeel et al., 2021c).

3.3. Two-step yielding model

In literature, several rheological models have been used to fit the flow curve of mud samples particularly for estimating the yield stresses such as Bingham model, Herschel-Bulkley model, Worrall-Tuliani model, Toorman model and Casson model (Babatope et al., 2008; Bai et al., 2002; Coussot, 1997; Huang and Aode, 2009; Messaoudi et al., 2018; Van Kessel and Blom, 1998; Xu and Huhe, 2016). For instance, the rheological properties of mud samples from Port of Rio Grande, Port of Santos and Port of Itajaí were investigated by fitting the flow curve data with the Bingham model (Fonseca et al., 2019). Likewise, Worrall-Tuliani model was used to fit the rheological experimental data of mud samples from two different locations of Hangzhou Bay, China (Huang and Aode, 2009). All these models are typically used to fit the flow curve of the sample with single step yielding. However, these models particularly Bingham and Herschel-Bulkley models can be used to capture the two-step yielding behaviour by applying these models in two different shear rate regimes defined by a critical shear rate (Huang and Aode, 2009; Xu and Huhe, 2016). For practical purposes, it is still useful to develop a model that can capture both yielding regions with a single equation.

Shakeel et al., (2021b) proposed an empirical model to capture the two-step yielding nature of mud, for the entire investigated shear rate range, by using the sum of two empirical expressions (one for each yield step). At lower shear rates ( $\dot{γ}$ ), the shear stress is depending on $τ_{s}$ and can be fitted by the function $τ_{s t a t}$ while at higher shear rates, the resultant stress is dependent on $τ_{f}$ and fitted by the function $τ_{f l u i d}$ , where the transition between the two functions occurs at a shear rate defined as ${\dot{γ}}_{0}$ . The model gives important rheological parameters of mud such as static yield stress ( $τ_{s}$ ), fluidic yield stress ( $τ_{f}$ ) and infinite viscosity ( $μ_{\infty}$ ) and is formulated as follows:(1) $τ = α τ_{s t a t} + (1 - α) τ_{f l u i d}$ where the step function $α$ is given by:(2) $α = 1 - \frac{1}{1 + \exp (- k (\dot{γ} - {\dot{γ}}_{0}))}$

This function gives $α (\dot{γ} < {\dot{γ}}_{0}) = 1$ and $α (\dot{γ} > {\dot{γ}}_{0}) = 0$ with a transition at $\dot{γ} = {\dot{γ}}_{0}$ , with a sharpness that depends on the value of $k$ . The function $τ_{s t a t}$ is given by:(3) $τ_{s t a t} = \frac{τ_{s}}{1 + {\dot{γ}}_{s} / \dot{γ}}$

From the analysis of this function, we find that:(3.1) $τ_{s t a t} ({\dot{γ}}_{s} ≪ {\dot{γ}}_{0}) = τ_{s}$ (3.2) $τ_{s t a t} (\dot{γ} = {\dot{γ}}_{s}) = \frac{τ_{s}}{2}$ ${\dot{γ}}_{s}$ represents the shear rate at which $τ_{s}$ is half of its value. The curvature of the first function can be tuned by varying ${\dot{γ}}_{s}$ . The second yielding step is captured by the function $τ_{f l u i d}$ given by:(4) $τ_{f l u i d} = τ_{s} + \frac{τ_{f}}{1 + {(({\dot{γ}}_{f} - {\dot{γ}}_{0}) / (\dot{γ} - {\dot{γ}}_{0}))}^{d}} + μ_{\infty} (\dot{γ} - {\dot{γ}}_{0})$

The coefficient $d$ enables to tune the “sharpness” of the curvature. The experimental data of stress ramp-up test is fitted with the proposed model (Eq. (1)) by using a Matlab script with the least square method, for mud samples from port of Hamburg. The model shows a good agreement with the experimental data (see Fig. 3).

3.4. Effect of density

Density (i.e., solid content and/or water content) is an important characteristic of mud which can significantly influence their rheological properties such as yield stress, thixotropy and moduli. For instance, Xu and Huhe (2016) observed an exponential increase in yield stress values of mud, collected from Lianyungang, China, as a function of volume concentration of particles. A similar increase in yield stresses as a function of solid content/density of mud is presented by other researchers as well (Carneiro et al., 2017; Fonseca et al., 2019; Soltanpour and Samsami, 2011). However, this density-yield stress correlation is observed to be significantly dependent on the organic matter content, sample collection and preparation (natural or diluted) and state of organic matter (fresh or degraded), which is explained in the next sections.

3.5. Effect of organic matter content

Organic matter in fine-grained sediments comes from (i) natural sources including eroded topsoils, plant litter, pelagic and planktonic biomass, or (ii) anthropogenic sources such as urban sewage and surface runoff, as listed in Zander et al., (2020). In suspended form, organic matter can interact with clay particles either by charge neutralization or by creating hydrogen bondsbetween the particles (Lagaly et al., 2013), forming a flocculated/aggregated system. In mud layers close to the ground, the floc concentration can become so large that the individual flocs encounter each other, and cross-floc bonds are formed. A large network is thus created and a transition from the fluid to mud establish. This is accompanied by a complex rheological behaviour of mud including viscoelasticity, shear thinning, thixotropic behaviour and two-step yielding (Coussot, 1997; Shakeel et al., 2020d; Van Kessel and Blom, 1998). For example, a substantial increase in yield stresses and complex modulus (Fig. 4a) was observed for mud samples having similar densities but with high organic matter content, which was attributed to the formation of a strong network (Shakeel et al., 2019a). The correlation between density and yield stresses was also observed to vary as a function of organic matter content for mud samples from different locations (with varying organic matter content) of port of Hamburg (see Fig. 4b) (Shakeel et al., 2021b).

3.6. Effect of dilution and organic matter degradation

In literature, the rheological properties particularly yield stresses of mud are investigated as a function of density either by diluting dense mud sample (Huang and Aode, 2009; Van Kessel and Blom, 1998) or by collecting natural mud layers with varying density (Shakeel et al., 2020d). Both these approaches can result in significantly different rheological behaviour of mud. Moreover, organic matter degradation under in-situ conditions can significantly influence the rheological properties of mud due to the breakage of clay-organic matter bonds or structural breakup of organic matter. The correlation between fluidic yield stress and bulk density for natural mud samples, artificially made mud samples (diluted) and anaerobically degraded mud samples is presented in Fig. 5. It is found that the degraded mud samples show intermediate behaviour of fluidic yield stress as compared to the other two types of samples. This result shows that the dilution of mud samples causes a significant decrease in yield stresses, which is attributed to the mixing effect imposed during the dilution along with the differences in the composition. Moreover, the dilution series of mud and the measurement of changes in rheological properties due to dilution are to be viewed critically because this process does not occur in nature. On the other hand, the reduction in yield stresses due to the degradation of organic matter is lower than the one observed for diluted samples. This information is very important for both laboratory studies where mud dilution is typically performed to investigate the density-yield stress correlation and also for in-situstudies where microbial degradation occurs as a function of time.