Evaluation of oil production related effects through geomechanical modeling: A case study from Marimbá field, Campos Basin, Brazil

1. Introduction

Geomechanics has evolved in reservoir development studies, and is already being used in innumerous oil fields, highlighting the importance of geomechanical modeling for reservoir behavior prediction. These predictions involve not only the actual stress state, crucial information for a successful well drilling campaign, but also on defining displacements, production, adopted production and injection pressure limits for the field and to better design mudweights. This knowledge is essential for optimal oil field project management, from the exploratory phase to the field abandonment. The Marimbá oil field use enables us to assess the geomechanical effects considering the reservoir geometry, its permoporous characteristics, the adopted production mechanism and the development project.

A 3D geomechanical model is proposed for the Marimbá field, located in the Campos Basin, southern offshore Brazil. The one-way coupling estimates the geomechanical effects due to the production process and analyzes them in the relevant time steps. Furthermore, this work integrates data from different supports and scales, an important step to obtain a reliable model. Thus, data such as well logs, injectivity tests, Leak-off Tests (LOT) and production history, as well as experimental rock mechanics tests, are taken into account in the proposed workflow.

2. Theoretical formulation

2.1. Coupling methods

Historically, reservoir simulation has accounted for rock mechanics in a simplified manner by using one single and constant value of rock compressibility.

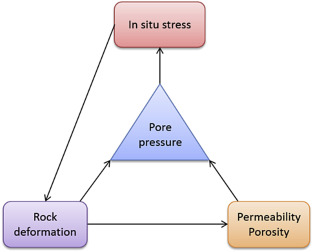
A better representation of hydromechanical behavior is necessary as the involved parameters are interconnected: the reservoir porepressure changes the in situ stress state, which modifies reservoir rock porosity and permeability. These will influence the pore pressure, renewing the process. This interconnection is outlined in Fig. 1.

To consider this interconnection in a numerical simulation, coupling between fluid flow and geomechanical modules (Herwanger and Koutsabeloulis, 2011, Angus et al., 2015) can be conducted considering four different approaches, namely: (i) fully coupled method; (ii) iterative method; (iii) explicit method; and (iv) pseudo-coupled method.

A detailed description of these approaches can be found in Sen and Settari, 2005, Tran et al., 2005 and David and Dupin (2007).

In general, fluid flow simulators use the finite difference method, while the stress analysis uses the finite element method. The following is a brief description of each coupling method mentioned above.

(i)
Fully coupled

The fully coupled method solves a single equation system in which the unknowns are pressure, temperature and displacements, using a single mesh. The method complexity makes this coupling type result with greater precision, but has the highest computational cost and the least flexibility. Possibly due to these characteristics, there are no commercial simulators of this class in the oil industry.

(ii)
Iterative or two-way coupling

In the iterative coupling method, also known as two-way coupling, the problem is divided into two modules that are solved separately and sequentially. From the flow module, which is the conventional simulator itself, the calculated pressure and temperature changes are transferred to the geomechanical module. Here, these changes are treated as external loading and used to calculate the displacements and, thereby, the stresses and strains. The properties obtained in the geomechanical module are now forwarded to the flow module through coefficients responsible for the porosity and permeability update. A new iteration is initiated in the flow module, where the pressure and temperature are recalculated and again sent to the geomechanical module. This process is repeated until the entire system converges, i.e., when the lowest tolerance criterion is reached, among pressure, stress and porosity (Tran et al., 2002). If the coupling frequency is sufficient to represent the rock behavior with the pressure changes and the convergence tolerance is low, this type of coupling could result in the same precision as the fully coupled case, but with greater flexibility and lower computational cost.

(iii)
Explicit or one-way coupling

In this coupling, the information exchange occurs in only one direction, hence the name “one-way”, from the flow simulator to the geomechanical. Pressure and temperature changes are calculated in the flow simulator and transferred to the geomechanical, inducing changes in stresses and strains. However, the effect of these changes does not return to the flow simulator, and is therefore not considered. In this case, the geomechanical module will only enable displacements and strains analyses resulting from pressure and temperature changes. Considered as a post-processing, the geomechanical module greatly increases the calculation speed. However, the reservoir behavior becomes totally independent on geomechanics, except for the rock compressibility, which is the only geomechanical parameter used in conventional reservoir simulation. In this approach, permeability is considered to be constant, without any strain effect in the porous medium.

(iv)
Pseudo-coupling

According to Samier et al. (2003), the pseudo-coupling method computes an approximate geomechanical response due to the compaction by using a table that relates pore pressure to porosity multipliers ( $M_{p o r})$ , as well as horizontal ( $M_{H p e r m})$ and vertical ( $M_{V p e r m})$ permeability multipliers, as follows:(1) $M_{p o r} = \frac{ϕ}{ϕ_{0}} .$ (2) $M_{H p e r m} = \frac{k_{h}}{k_{h 0}} .$ (3) $M_{V p e r m} = \frac{k_{v}}{k_{v 0}} .$

The horizontal permeability is represented by $k_{h}$ and vertical by $k_{v}$ on pressure $P$ , while the initial horizontal and vertical permeability are represented by $k_{h 0}$ and $k_{v 0}$ , respectively.

In conventional reservoir simulation, porosity is updated following the equation:(4) $ϕ = ϕ_{0} [1 + C_{p} (P - P_{r e f})],$ where $P_{r e f}$ is the reference pressure at which the initial porosity $ϕ_{0}$ was obtained, and $C_{p}$ is the pore compressibility. When using the pseudo-coupling, the porosity update is no longer made through Equation (4), but by means of multipliers. Additionally, the permeability is also updated through Equations (2), (3)). Falcão (2013) applied this method to study a synthetic oil field and obtained satisfactory results compared to fully coupled method at a lower computational cost. This indicates the method is feasible to be incorporated into routine reservoir production management studies.

In this study, the one-way coupling method was adopted, which is characterized by the exchange of information in only one direction, from the fluid flow to the geomechanical module. In-house software based on the finite element method (Sousa et al., 2010, Laquini and Sousa, 2011) was used.

2.2. Stress path

During reservoir compaction, the vertical stress remains constant, while the horizontal stresses change during depletion (Fjaer et al., 2008). To understand the stress path parameters, it is helpful to review the concept of effective stress. The stress path concept is based on Terzhagi effective stress principle and is expressed in Equation (5), assuming compression is positive:(5) $σ^{'} = σ - α P_{p},$ where $σ^{'}$ is the effective stress, $σ$ is the total stress, $P_{p}$ is pore pressure, and $α$ is Biot's coefficient.

The stress path parameters are defined by three terms, the stress arching parameter $γ_{v}$ , the horizontal stress path parameter $γ_{h}$ and the deviatoric stress path parameter $K$ . Segura et al. (2011) defined $K$ and $γ_{h}$ as function of the rock Poisson's ratio: $K = ν / 1 - ν$ and $γ_{h} = α (1 - 2 ν / 1 - ν)$ , if no stress arching is taking place. Also the parameters can be defined in terms of the effective stresses (see Fjaer et al., 2008, Segura et al., 2011, Angus et al., 2016), as $γ_{v} = Δ σ_{v} / Δ P_{p}$ ; $γ_{h} = Δ σ_{h} / Δ P_{p}$ and $K = Δ σ_{h}^{'} / Δ σ_{v}^{'} or K = γ_{h} - α / γ_{v} - α$ , where $Δ σ_{v}^{'}$ and $Δ σ_{h}^{'}$ are the incremental effective vertical and minimum horizontal stresses respectively, and $Δ P_{p}$ is pore pressure variation.

The parameter $K$ , which will be analyzed further in this study, describes the stress anisotropy development, and therefore the likelihood of shear failure or pore collapse in the material.

3. Geological context

The selected study dataset corresponds to the Marimbá oil field. A turbiditesandstone reservoir from the Santonian/Campanian Age of the Cretaceous Period. Situated in the Campos Basin, approximately 80 km from Macaé, Rio de Janeiro State, southern offshore Brazil.

3.1. Field characteristics

The Campos Basin Marimbá oil field is in water depths ranging from 300 m to 800 m, with an area of approximately 50 km2. There are in the Marimbá oil field seabed, a canyon with more than 200 m deep canyon, as shown in Fig. 2.

The reservoir rocks belong to the Carapebus Formation and are composed of amalgamate channels of turbidite sandstones from the Santonian/Campanian Age of the Cretaceous Period. The reservoir thickness ranges from 10 m to 190 m, with an average thickness of 50 m (Becerra et al., 2011).

According to Lima et al. (2001), the reservoir rocks are predominantly massive turbidite sandstones, with grooved canyon filling system features and large areal distribution. Its petrophysical characteristics are good, being 25% average porosity, 1 500 mD average permeability, 29° API density oil, and 2.1 cP viscosity. Structurally, the Marimbá field presents normal faults, typical of a normal tectonic regime. A structural compartmentation separates the field into blocks, but it has a good hydraulic connection by an aquifer.

This field holds a 100 million m3 volume of oil in place (VOIP). Discovered in the beginning of 1984, its production began in April 1985, reaching the peak with a 10,000 m3/day average production rate in 1994. After 14 years of production, the field was still producing 6800 m3/day, without any water injection. At that time, the cumulated oil production had reached 27 million m3, bringing its original pore pressure down from 281 kgf/cm2 (27.6 MPa) to 180 kgf/cm2(17.7 MPa), that is, nearly a 100 kgf/cm2 (∼10 MPa) depletion (Lima et al., 2010). This depletion represents an important aspect for the Marimbá reservoir geomechanical evaluation.

From 1994 to 2010, the Marimbá oil field achieved its highest oil production rate, as shown in Fig. 3a, with two average production levels: an initial plateau of 12,000 m3/day from 1994 to 2005, and a second plateau of 14,000 m3/day from 2005 to 2009, reflecting the water injection which began in 2002. Therefore, the period between 1994 and 2005 was the one during which most petrophysical properties might have changed and, consequently, the geomechanical properties too. The period from October 1993 to June 2002 was the worst in terms of injection-production balance, as can be seen in Fig. 3b, with an average deficit of almost 12,000 m3/day.

In mid-1993, water production began and reached its peak in 1999 with 34% BSW. An issue to be considered, when compared to the production history data, the Marimbá oil field production curves seemed to have been overestimated. This mismatch is a consequence of its model non-representativeness, and may be due to some other factors, such as an inadequate geological model, or an incorrect fluid characterization or even due to the fact of neglecting geomechanical effects.

4. Geomechanical modeling methodology

The first step was to search for the necessary data sources to construct a 3D geomechanical model, which included well logs as caliper, image (acoustic and resistive), P and S waveform (DTC and DTS, respectively), and density (ρ). In addition, laboratory data are very important for reservoir-rock characterization, as it represents information obtained directly from the core. Among the laboratory data, the petrophysical and mechanical tests were fundamental. In situ fracturing experiments, such as Minifracs, has its relevance in the studied field to determine the reservoir stress state. The main surfaces that delimit the reservoir (top and bottom), besides the regional surfaces that identify the relevant lithological differences in every rock column adjacent to the reservoir (over-, under-and sideburden), as well as the most important faults, make up the geomechanical model structural framework.

The proposed methodology, illustrated in Fig. 4, is composed of six main stages:

1.
Poisson ratio (ν) and Young modulus ( $E$ ), cohesion ( $c$ ) and friction angle ( $\emptyset$ ) estimated from well logs, calibrated with laboratory data; and $ϕ, κ, P p and S$ (saturation) imported from flow simulation;
2.
Geomechanical grid construction, using the regional horizons and the horizons corresponding to the reservoir top and bottom surfaces, considering their stratigraphic equivalents to extend them until the model limits;
3.
Geomechanical grid population with elastic and strength properties computed in step 1; and the reservoir properties ( $ϕ, κ, P p, S$ ) imported from flow simulation. The geomechanical model is ready and then can move on to the next step;
4.
Model initialization and validation, by comparing the numerical stress state estimated to the in-situ measurements;
5.
Selection of the relevant time steps for the one-way coupling and perform the geomechanical simulation;
6.
Analyses of the geomechanical model results.

Each process inherent to the methodology will be detailed throughout this work.

4.1. Estimating strength and elastic properties

Elastic and strength properties influence the subsurface stress and strain distribution.

Initially, the objective is to correlate elastic wave descriptive parameters and those descriptive of the reservoir and adjacent rock properties.

There are no direct methods available to determine the strength parameters in situ. Hence the estimative of strength parameters is made based on empirical correlations, especially related to acoustic velocities.

4.1.1. Cohesion and friction angle

Equation (6) is generally referred to as the Coulomb equation and is commonly used to describe the strength of soils.(6) $c = τ - σ t g Φ$ in which, c is the cohesion (the intercept on the shear stress axis - KPa), $Φ$ is the friction angle (indicates the slope of the line - degrees).

According to Lal (1999), friction angle may be estimated by:(7) $s e n Φ = V_{p} - 1 / V_{p} + 1.$ Where: $c$ = cohesion (MPa); $Φ$ = friction angle (degrees); $V_{p}$ = P wave velocity (km/h).

4.1.2. Poisson's ratio and Young modulus

The linear elasticity theory deals with situations where there are linear relationships between applied stresses and resulting strains. Poisson ratio and Young modulus are the most commonly used elastic properties in geomechanics.

The Poisson ratio ( $ν$ ) name is a tribute to the French mathematician Siméon Denis Poisson (1781–1840). It is defined as a dimensionless magnitude that relates the transverse and longitudinal strains, varying between 0 and 0.50. According to Duarte (2014) some typical Poisson ratio values are:

✓
sandstone with oil: 0.10 up to 0.24;
✓
sandstone with water: 0.35 up to 0.42;
✓
shale: 0.28 up to 0.34;
✓
anidrite: 0.28 up to 0.34;
✓
carbonates: 0.25 up to 0.37.

The Poisson ratio can be estimated from acoustic logs, as described in Equation (8) (Santos and Ferreira, 2010, Fjaer et al., 2008).(8) $ν = 1 - (1 / 2 - 2 {(V_{s} / V_{p})}^{2}) .$ Where: $V_{s}$ = shear wave velocity.

The Young modulus ( $E$ ), or Elasticity modulus or even Deformability modulus, measures rock stiffness, relating deviatoric stress to axial strain. The name is a tribute to the English philosopher Thomas Young (1772–1829). Some usual values, measured through rock mechanics laboratory tests are (Fernandes, 2007):

✓
limestone: 20–50 GPa;
✓
sandstone: 15–60 GPa;
✓
soil (compressed): 0.01 up to 1 GPa.

The dynamic Young modulus can be predicted in terms of velocities by Equation (9) (Fjaer et al., 2008):(9) $E_{d y n} = 2 ρ (1 + ν) V_{s}^{2} .$

Based on Zoback (2008), low porosity sandstones (0–6%) are characterized by the Young modulus around 50 MPa, while its Poisson ratio is approximately 0.125; on the other hand, those with high porosity (>16%) present lower values of the Young modulus and higher Poisson ratio values.

Dynamic and static terminologies are applied to define the frequency used during elastic property measurements. Static properties may be obtained from rock mechanical laboratory tests, whilst those called dynamic are measured using high frequency methods, e.g., well logs, mainly velocity and density, and seismic data. For further study of the topic, suggested references are Fjaer et al. (2008) and Mavko et al. (1998).

However, static properties are those that better represent the stress-strain rock behavior. Considering that there is a higher availability of dynamic data, correlations between dynamic and static elastic parameters should be used to populate geomechanical models. Nevertheless, it has been verified that the already proposed equations correlating dynamic to static Poisson ratio do not result in a reasonable fit. For this reason, a common practice is to adopt the same values for dynamic and static Poisson ratio. For the static Young modulus ( $E_{s t}$ ), a conversion is used. Among others, Lacy (1996) presented a correlation described in Equation (10) which is widely used in industry, and is based on shale, sandstones, calcilutites and dolomites samples from the USA, Canada, South America, Russia and the North Sea.(10) $E_{s t} = 0.0293 E_{d y n}^{2} + 0.4533 E_{d y n} .$

In 1995, Dillon et al. proposed a correlation between static and dynamic Young Modulus obtained from simultaneous measurements on core samples from the Campos' and Santos’ Basins reservoirs, as follows:(11) $E_{s t} = 0.675 E_{d y n} - 3.84.$

This study also used Equation (11), as it was elaborated using rock samples that can be considered analogous to the Marimbá field.

4.1.3. Biot coefficient

Biot coefficient ( $α$ ) represents pore pressure contribution on loading support, along with the solid matrix. It is dimensionless, and varies from 0 to 1. The closer to 1, the greater will be the contribution of the fluid to bear the load (Vasquez et al., 2011). Besides, Biot coefficient behaves as a coupling parameter (Santos et al., 2015). In accordance with Wang, 2000, the $α$ can be estimate by Equation (12):(12) $α = 1 - (K_{b} / K_{g}),$ where $K_{b}$ is the rock's bulk modulus (including solid matrix and pores), that can be calculated by Equation (13); and $K_{g}$ is the grain's bulk modulus.(13) $K_{b} = E / 3 (1 - 2 ν) .$

4.2. Building the geomechanical mesh

In the geomechanical mesh, besides the reservoir, also its adjacent rocks, over-, under- and sideburden, should be represented, as schematically shown in Fig. 5a. Thereby, beyond contextualizing the reservoir within its structural framework, it also seeks to mitigate border effects. For this purpose, five surfaces interpreted in the seismic data covering the entire geomechanical meshwork areal extension were used. These are: the seabed; the blue mark that corresponds to a regional horizon observed in different fields within the Campos Basin; the reservoir top and bottom; and the bottom surface of model. As the reservoir, top and bottom surfaces do not cover the whole geomechanical model extension, they were extended to ensure the entire reservoir interval is distinguished throughout the mesh area, thus reaching the model boundaries. The reservoir flow simulation grid is also used as an input to generate the geomechanical mesh. The Marimbá flow simulation grid consists of more than 4 million cells, including active and non-active cells (151 and 122 cells in the horizontal directions I and J, respectively, and 233 in the vertical direction K) and contains complex features such as those shown in Fig. 5b. These pinchouts are not adequate for the stress analysis software used in this study, because there are non-coincident nodes. Therefore, a new structured mesh was generated, similar to the original in terms of porosity and pressure distributions, but maintaining a minimum thickness interval beyond the pinchout terminations.

In the reservoir, the same original model horizontal discretization was maintained i.e., approximately 75 m in each horizontal direction. As for the vertical, 122 x 4-m thick layers were used, to maintain, to the maximum, the reservoir information from the simulation model. In the overburden, the mesh was discretized using 49 layers with varying thicknesses, gradually increasing from the reservoir top to the seabed. To smooth between one region and another, just above the reservoir top 28 × 10 m thick layers were used, above these 4 × 20 m layers and other 17 × 100 m thick layers until reaching the seabed. In the underburden, to maintain certain proportionality, 13 layers were used, 2 × 40 m thick layers immediately below the reservoir bottom and other 11 × 200 m thick layers below those. The geomechanical mesh with its vertical discretization is shown in Fig. 6.

The elements contained in the reservoir measured 75 × 75 × 4 m, while those in the sideburden were 375 × 75 × 4 m at the reservoir level interval. In the interval above it, the configuration was 375 × 375 × 10, 20 or 100 m and in the interval below it was 375 × 375 × 40 or 200 m, as the layer thicknesses increased above and below from the reservoir, as already mentioned. The same approach was used in the overburden and underburden, with element dimensions of 75 × 375 × 10, 20 or 100 m and 75 × 375 × 40 or 200 m respectively, following the gradual layer thickness increase. This mesh pattern was the best fit for the studied reservoir.

Yin et al., 2009 emphasized the importance of modeling the adjacent rocks, studying their effects on pressure and saturation over time. It was observed that a redistribution of effective stress was not a local process, occurring in a more extensive domain that involved, not just the reservoir, but the entire overburden, underburden and sideburden rocks out to considerable distances.

Fig. 7 illustrates the elements distribution within the geomechanical mesh, considering all the surrounding rocks horizontal dimensions. The model has approximately, a total of 6 million elements. Region 1, in the mesh center (yellow), represents the reservoir with elements of 75 m × 75 m dimension in X and Y directions. Around of reservoir are the extended regions to represent the surrounding rocks. Region 2 (blue) elements dimensions are 75 m × 375 m (X-Y directions). In the same way, region 3 (light orange) elements have dimensions of 375 m × 75 m. Finally, region 4 (green) elements are 375 m × 375 m.

4.3. Populating the geomechanical mesh

Considering the reservoir and the sideburden region located at the reservoir depth, elastic and strength properties were estimated using the equations presented in section 4.1. The Poisson ratio and Young modulus values were estimated for each well considering Equations (8), (11), whilst the density values were obtained directly from the well logs. After this step, the vertical trend curves for each property, along each well path were generated. The method used to perform simulations was the Sequential Gaussian Simulations (SGS). There are many methods to perform stochastic simulations of continuous variables (Fast Fourier Transform FFT, Turning Bands, etc.), but SGS is the most used for its efficiency and simplicity. The sequential algorithm was suggested by Alabert (1987) and Journel and Alabert (1989) describing Sequential Indicator Simulations (SIS). Its extension to the multi-Gaussian field was proposed by Isaaks (1992) in a context of mineral development. The idea of sequential simulation is to assign the data status to the previously simulated values and thus ensure the covariance among all the simulated data will be reproduced and equal to that used in the kriging process.

Gaussian formalism is the simplest method to generate realizations of a random, stationary function and that honours existing data, the histogram of these data, and the spatial covariance. The main SGS steps are: 1. transform the original data distribution into a normal distribution; 2. perform a simple kriging, at each grid node, to obtain an estimate and its corresponding kriging variance; 3. sort a residue from a Gaussian distribution with null mean and variance equal to the kriging variance obtained in the previous step; 4. Add the residue to the kriging estimate to obtain the simulated value.

SGS is a widely used method to simulate continuous reservoir properties such as porosity or permeability in reservoir modeling workflows (Deutsch and Journel, 1992, Deutsch, 2002). The skill in SGS is to have a feedback loop and incorporate previously simulated values as an extra data point, is the key to ensure that the simulations are spatially correlated (Doyen, 2007). Thereby, the SGS were performed to fulfill the data within the grid, and the simulations restricted so that each layer respected the curves generated in the previous step, as well as respecting the well data.

Once the simulations were completed, the results were averaged to smooth out the estimated properties. For the elements representing the reservoir, porosity and pressure values were interpolated from the flow model to the geomechanical grid.

Finally, in the over and underburden areas, for which there was no log information, correlations from other neighboring fields, where well logs have been registered, were used. Some properties used in the geomechanical analysis are represented in Fig. 8. Regarding cohesion and friction angle properties, they were considered to be constant and equal to 0 and 30° respectively, considering the Mohr-Coulomb criterion, representing a more conservative reservoir rock scenario.

Analyzing the elastic property histograms, the Poisson ratio shows a higher frequency distribution for values between 0.35 and 0.38. The Young modulus shows values ranging from 1 420 to 37,321 MPa, with higher frequencies between 4 000 and 8 000 MPa, compatible with high porosity turbiditesandstone cited by Zoback (2008).