Development of scaling criteria for enhanced oil recovery: A review

1. Introduction

Scaled physical models have been extensively used in the field of engineering problems to reproduce the behavior of an actual system on a small-scale laboratory for many years (Doscher, 1980). This process is effective to simulate the behavior of a petroleum reservoir and efficient in evaluating the advantages of a recovery process (Purvis and Bentsen, 1988). Their significance has been demonstrated particularly for new processes whose mechanisms are not well understood or a mathematical description is difficult to formulate. The procedure for the development of scaled models will be accepted when dimensionless scaling groups would be known to scale up laboratory results to field conditions. The world has huge natural resources (e.g., fossil fuel). Most of the fossil fuel in the form of heavy oil reserves are found in Canada. These unconventional resources have been deposited in unfavorable conditions. Thus, it needs more efforts, technological advancements and energy to recover the reservoir fluid. In practice, three-dimensional (3D) displacement models can represents an appropriate well configuration. However, their physical limitations make it impossible to duplicate the real reservoirs under some conditions. Therefore, it is essential and of pragmatic significance to create scaling criteria for depicting the fluid behavior in unconventional reservoirs (Zhou, 2015). Although, recent advancements in numerical reservoir simulationprocesses are significant, however scaled physical models are presently favored because their capacity to capture the physical phenomena that can occur in a specific process. In the petroleum engineering, core flood experiments in the laboratory have been used for many years to understand, and verify the reservoir behavior and numerical findings. The feasibility of EOR techniques are investigated through this process before they are attempted in the field application. Whatever information is obtained from a pore scale model, it should be presented in a way such that it will be appropriate for other systems rather than the one used. As results are described, it is practical to use the outcome of one scale to foresee the behavior of another scale. A series of connection should be developed to verify the approximations between the two configurations which are considered for the analyses. The developed connections between two systems are typically known as similarity laws, similarity requirements, or scaling laws. These scaling laws help to develop the specific EOR process which can affect the physical phenomena.

1.1. Enhanced oil recovery

EOR is the implementation of different kinds of secondary and tertiary recovery techniques. It can be employed for increasing the amount of crude oil that can be extracted from an oil field. Different types of technologically advanced EOR techniques have been developed over the last thirty years for mature and depleted type reservoirs (Ali, and Thomas, 1996). These techniques greatly enhanced the effectiveness of oil recovery compared to the primary (i.e. pressure reduction), and the secondary (i.e. water flooding) recovery techniques. In the most recent times, EOR techniques have paid attention from the field development and research work stages to enhance the recovery of a specific field. This increased attention has been promoted by high oil price, increased demand, the expansion of oil fields around the world, and new well discoveries (Aladasani and Bai, 2010). Two-thirds of the oil volume in the reservoirs require unconventional EOR strategies for recovery (Green and Wilhite, 1998). Different types of reservoirs are available on earth. So, different types of EOR techniques are developed to improve the extraction of oil & gas from the reservoirs. Several techniques had been used so far to increase the recovery of oil. Gas and thermal flooding are the most widely used and successful recovery methods that consist of around 99% of EOR in the United States. Chemical and microbial EOR methods have research potential. However, these techniques require high operating cost with relatively low performance. Thermal EOR techniques are usually applied to heavy viscous crude oil reservoirs. This method involves the introduction of heat or thermal energy deep into the reservoir to raise the temperature of the reservoir fluid (e.g., oil). Thus, the viscosity of reservoir fluid will decrease which will ultimately increase the mobility ratio as well as sweep efficiency (Mozaffari et al., 2013). Many Laboratory experiments and analyses have been conducted over the years to accomplish this goal. Different types of experiments and analyses were conducted to study different mechanisms. Some analyses, known as numerical simulation were designed to present the results which can be extended to predict the field production. On the other hand, some other experiments known as scaled experiments were considered to permit the relative impact of other mechanisms observed in the laboratory experiments.

1.2. Scaled model studies

Scaled model studies provide an accurate method for forecasting reservoir fluid displacement. This method is used to study the impact of different factors on the recovery of hydrocarbon. The scaling technique utilizes the outcomes gained at one scale dimensions (laboratory research scale) to extrapolate at alternative scale dimensions (a large-scale method) (Buckingham, 1914, Lozada and Ali, 1987, Shook et al., 1992, Johnson, 1998, Gharbi, 2002, Novakovic, 2002). In case of isothermal or non-isothermal petroleum reservoirs, different scale models have been documented to describe multiphase fluid flow behavior. Scaling should be performed properly because unscaled laboratory experiments may be misleading when applied to field operations. Some variables in laboratory experiments might be unduly amplified, while other vital variables might be smothered. In recent years, complex numerical simulators have been built with effective and dependable computational schemes. Similarly, high performance and CPU storage capacity computers are also available. These systems still suffer from computational time and storage. It is difficult for numerical simulators to give detailed descriptions of an extensive field containing heterogeneities. In contrary, it is relatively easy to implement the physical models. Therefore, in describing the physical process of a reservoir scheme, scaled models play a crucial role. This scale method can be used to verify computational strategies. It can provide information of certain physical phenomena which are not appropriately formulated in numerical simulators. The laboratory models have been used for many years to simulate the actual behavior of a reservoir during the thermal recovery schemes. The development of scaling criteria for thermal recovery processes are more difficult in small laboratory models. Many factors such as heat transfer, thermal effects on rocks and fluids, as well as capillary, gravity and viscous forces should be considered. The theory of similarity between model and prototype were considered as a base to outline a scaled physical model. In terms of geometric similarity, flow rate, pressure drop and time factor which are different for different approaches are exemplified by these processes. Depending on the variables used, each method has its distinctive benefits and shortcomings (Bansal and Islam, 1994). It is very challenging to fulfill a complete set of scaling principles prerequisite to design a thermal recovery process. Thus, some of the similitude numbers must be undisturbed to fulfill the most significant factor of a reservoir behaviors. The selection of which requirement should be relaxed be governed by the specific process being modeled. A specific process should be rested without essentially disturbing the significant element of the process which can be considered as a scaling phenomenon.

1.3. Dimensionless scaling group

The ultimate objective of the scaling technique is to forecast the behavior of rock and fluid properties which affect the physical phenomena from laboratory scale (i.e. small) to field scale (i.e. large). Dimensionless scaling groups are developed using appropriate parameters so that the dynamics of the physical system remain essentially unaffected. The scaled parameters have the connections between themselves which are assigned by different scaling techniques. Here, we considered the two methods. The first method is the classical scaling methodology which is known as a dimensional analysis process. It is constructed in dimensionless groups of parameters that can be set up by using the Buckingham $π -$ theorem. The second procedure involves governing equations with initial and boundary conditions. It can determine relationships among variables through scaling transformations.

1.4. Motivation and purposes

Widespread research efforts have been dedicated in the field of EOR by water flooding, steam flooding and other recovery techniques (Alvarado and Manrique, 2010). Several investigators focused on water flooding EOR techniques, while comparative studies of different EOR techniques have been done by others. Development of various types of dimensionless groups by dimensional and inspectional analyses has also been accomplished for different forms of EOR techniques. Those developed dimensionless groups were validated using the core flood experiments and numerical simulation. However, how these experiments were planned and performed to improve the mobility and sweep efficiency has not been presented properly. On the other hand, there is not much work done for developing scaling principles in the field of thermal flooding EOR techniques. As the scale of measurements from labs to reservoirs increases, steam flooding requirement increases rapidly and the effects of reservoir heterogeneity are emphasized. Dimensionless scaling groups can be used to characterize the reservoir fluids and rocks properties for better explanation of the complex rock/fluid behavior. In the future, these dimensionless scaling groups can be employed in displacement process to augment the recovery technique and enhance the production of oil from the reservoirs.

2. Scaling approaches

The studies on the method of dimensional analysis or dimensionally scaled models have been applied to engineering problems for many years; especially in the field of heat and fluid flow along with structural design (Bridgman, 1931, Langhaar, 1951, Leverett et al., 1942, Mattax and Kyte, 1962, Murphy, 1950). A similar application for petroleum reservoir problems is relatively new but the application is increasing day by day (Bobek and Bail, 1961, Carpenter et al., 1962, Craig et al., 1955, Craig et al., 1957, Engelberts and Klinkenberg, 1951, Geertsma et al., 1956, Graham and Richardson, 1959, Henley et al., 1961, Leverett et al., 1942, Mattax and Kyte, 1962, Rapoport, 1955, Rapoport and Leas, 1953, Seve and Pottier, 1963, Van Meurs, 1956). Dimensionally scaled models are particularly important in deciding the behavior of reservoirs with unsymmetrical limits and different well-spacing patterns. These properly scaled physical model studies and their pertinent variables are the most important factor for complex fluid displacement processes in porous media.

Dimensionless scaling groups provide a technique by which we can study analogous methods on diverse scales. Small-scale operations are carried out to simulate such approaches. Ultimately, it will help to understand or predict the larger scale (i.e., field) processes. It is important to generate a group of relationships starting from small scale laboratory studies towards larger scale field operations. These relationships will connect both systems which are known as scaling laws. Dimensionless numbers are used to represent these scaling laws. In the literature, there are two existing methods available in finding dimensionless numbers, which are dimensional analysis (Buckingham, 1914, Bridgman, 1931, Langhaar, 1951, Focken, 1953, Nielsen and Tek, 1963, Sonin, 2001) and inspectional analysis (Ruark, 1935, Birkhoff, 1950, Bear, 1972, Shook et al., 1992, Novakovic, 2002).

2.1. Dimensional analysis

The procedure that combine different type of parameters or factors into a group which is essentially dimensionless and have an impact on a specific process is called dimensional analysis. The impact of a specific parameter is then considered in terms of a group instead of separate parameters within the group. Dimensional analysis remains as the most useful technique in areas where knowledge is developed through a middle stage. It can be applied when fundamental laws are now known, and the absence of capable techniques for solution. Bridgman's dimensional analysis (Bridgman, 1931) technique found widespread applications in engineering and physics. Rapoport (1955) proposed that if the proportion of dimensionless group on a smaller (laboratory) geometric scale to that on a larger (field) geometric scale is kept equivalent to unique, then the activities appearing on both scales should be analogous. Nonetheless, if both scales are geometrically related then the above description is correct. Dimensional analysis was first adopted in developing dimensionless groups for the investigation of reservoir behavior by Leverett et al. (1942).

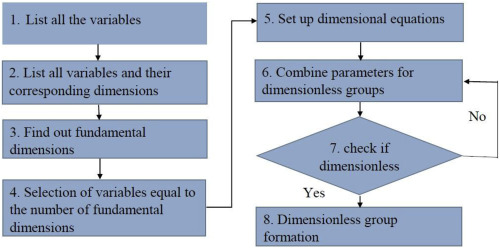
The procedure of dimensional analysis is shown in Fig. 1. First, each parameter that affect the specific process and their corresponding dimensions for performing dimensional analysis should be listed. Then the fundamental dimensions including length, mass, temperature, time, etc. for this specific process should be found out. Selection of variables should be equal to the number of fundamental dimensions. After that, the dimensional equations should be set up and combined the parameters to form dimensionless groups. Finally, check if the derived group is dimensionless or not. If the group is not dimensionless, then performed the previous step again to make it dimensionless.

2.2. Inspectional analysis

Inspectional analysis is a procedure where the dimensional analysis procedure is expanded. This approach verified the dimensionless expression in contrast to the parameters it has been generated. We can develop the dimensionless groups experimentally without the help of governing equations for dimensional analysis. However, for inspectional analysis, governing equations should be derived with the help of initial and boundary conditions. It is a straightforward, easy and preferred technique for deriving the dimensionless scaling group in petroleum literature. All equations which describe the method of concern are considered to form a single differential equation. The parameters of the equation form the dimensionless groups. This method has a unique advantage that the developed scaling groups have a clear physical meaning. As inspectional analysis involves parameters rather than dimensions, so it can produce dependent dimensionless groups which affect a specific process. The procedure for inspectional analysis is presented in Fig. 2.

2.3. Comparison of scaling approaches

Dimensional analysis is useful in providing directions for initial analyses. It is particularly helpful when there is a lack of data and information. In this manner, the dimensional analysis technique is widely used than the inspectional analysis technique because it needs only a little theory to perform dimensional analysis. It can also provide an initial direction in setting up the investigations. Dimensional analysis is rapid and simple process. It often yields required information. There are scaling groups introduced using the dimensional analysis which would not be possible using inspectional analysis. Some of the variables were not considered in the formulation of the governing equations. On the other hand, dimensional analysis has some limitations. There may be extra groups formed by dimensional analysis which may not affect the physical process. The physical meaning of these groups may be quite obscure. For example, there are two groups which are related to inertia forces and these are Reynolds number $(ρ v k^{\frac{1}{2}} / μ)$ and the ratio $(k / L^{2})$ which is related to pore diameter and overall dimensions. For cases of practical interest, inertia effects may not be important, thus we can relax their scaling requirements (see Fig. 3).

The inspectional analysis strategy is used for most reservoir engineeringapplications. The partial differential equations and boundary conditions are derived using the most important basic physical principles (Shook et al., 1992). The fluid flow equations should be incorporated in the analysis to explain the behavior of a reservoir more clearly. The principal objective of the inspectional analysis is to describe the natural phenomena which occur in the reservoir. This approach can use extended group of equations with the required boundary conditions. Usually, inspectional analysis can form dimensionless scaling groups whose physical significances are evident and which will affect the physical process. On the other hand, inspectional analysis needs mathematically derived formulations for the study of the process involved. If such equations are not available, inspectional analysis cannot be used. Although, the inspectional scaling approach represents the derived equations with minimum parameters, implementation of this procedure is tedious and time consuming.

Finally, dimensional analysis involves generating dimensionless groups, irrespective of whether it is related to a specific process or not. Thus, we can get a meaning less result in terms of a specific process involved. In contrary, inspectional analysis produces dimensionless groups in a way that the developed groups can affect a specific process. In conclusion, if the initial and boundary conditions are chosen in a proper way to formulate the involved equations, then the difficulty level should be minimized.

3. Development of various scaling criteria

This review is based on various scaling criteria of fluid flow through porous media for fluid displacement processes within petroleum reservoirs. Scaling groups are very important in describing the influence of parameters on a specific EOR process. Accurate formulation and evaluation of dimensionless scaling groups are important because it can largely affect the physical process. Unscaled physical processes can give erroneous results. Table 1 lists the most widely used scaling groups relevant to EOR.

Table 1. Various scaling dimensionless numbers (Novakovic, 2002).

Dimensionless scaling type	Scaling group	Formulation	Comment
Physical Effects of Flow and Fluid Properties Scaling	Capillary Number	$N_{C} = \frac{F_{c a p i l l a r y}}{F_{v i s c o u s}}$	Rock-fluid interaction, describes set-up at the small scale
	Gravity Number	$N_{g} = \frac{F_{g r a v i t y}}{F_{v i s c o u s}}$	Reservoir-fluid shape dependent, seizures the effect of resistant force
	Mobility Ratio	$M = \frac{λ_{d i s p l a c e d f l u i d}}{λ_{d i s p l a c i n g f l u i d}}$	Fluid-rock-fluid communication effect on the flow performance
Displacement Techniques with Initial and Boundary Conditions Scaling	Displacement Efficiency Factor	$E_{D} = \frac{V_{P r o d u c e d}}{V_{R e f e r e n c e}}$	Dimensionless production response
	Dimensionless Time	$t_{D} = \frac{V_{i n j e c t e d}}{V_{p o r e}}$	Forced injection boundary condition
Reservoir Geometry Scaling	Aspect Ratio	$N_{A} = \frac{L}{H}$	Reservoir shape description scale
Reservoir Geometry Scaling	Dip Angle	$N_{α} = tanα$	Dip angle scaling

3.1. Capillary number

The ratio of viscous force to capillary force is termed as capillary number (Fulcher et al., 1985, Tang, 1992). Different forms of capillary number have been used in the existing literature (Cense and Berg, 2009). Foster, 1973, Salager, 1977, Green and Wilhite, 1998, and Tiab and Donaldson (2015) defined the capillary number using the Darcy velocity of displacing fluid, the viscosity, porosity and the interfacial tension. Sheng (2010) omitted the porosity term and Lake (1989) included the contact angle term. The derivation of capillary number can be found in the literature (Johannesen and Graue, 2007). The capillary number provides satisfactory correlations of mobility of oil with respect to different values of viscosities (Morrow, 1979). The recovery factor is found to be dependent on the capillary factor (Fulcher et al., 1985).

3.2. Bond number

The ratio of the gravity force to the capillary force is called the Bond number. It is of great importance in vertical displacement processes in a reservoir-well system. The Bond number is usually useful for gravity assisted displacement processes. For immiscible displacement process oil recovery improves with increasing Bond number.

3.3. Gravity number

Gravity number which characterizes the ratio of gravity to viscous force is a dimensionless group. It does not detect the properties of the capillary forces. Gravity number depends on gravity, oil and gas density and viscosity, absolute permeability and the gravity drainage velocity of the fluid. The gravity number indicates that the gravity effects are larger in thicker reservoirs and higher the gravity number the better would be the recovery.

3.4. Mobility ratio

The ratio of effective permeability to phase viscosity of a fluid is expressed as the mobility ratio. The proportion of the mobility of displayed fluid by displacing fluid is termed as mobility ratio of one fluid by another in terms of displacement process. The fundamental mechanism behind the displacement of oil by water can be grasped through studying the mobilities of the individual fluids (Dake, 1978).

3.5. Displacement efficiency

The portion of movable oil that can be extracted from the reservoir using existing technology at any time is defined as the displacement efficiency. The microscopic displacement efficiency is dependent on the mobilization or dislocation of oil at the small scale. It can be a criterion for the preliminary oil saturation or remaining oil saturation in the area contacted by the moving fluid. On the other hand, macroscopic or volumetric displacement efficiency depends on the efficiency of the moving fluid in contact with the reservoir in a volumetric sense. The macroscopic displacement efficiency of a fluid can be measured in a way by which the displacing fluid is striking the reservoir volume both areally and vertically.

3.6. Dimensionless time

The scale-up time of a given prototype field is expressed by the dimensionless time. The expression of dimensionless time (td) can be found in the literature (Miguel-H et al., 2004), for the gravity drainage methods and is stated as:(1) $t_{d} = \frac{k k_{r o} Δ ρ g (\frac{K}{ϕ}) / g_{C}}{h ϕ ρ μ_{o} (1 - S_{o r} - S_{w i})} t$

Equation (1) enables estimation of the time required in the reservoir to reach the same recovery as the scale-up of the run time (in minutes) in the physical model.

3.7. Aspect ratio

The proportion of a geometric shape magnitude in diverse dimension is called the aspect ratio of that shape. For illustration, the proportion of width to height or the ratio of longer side to shorter side is defined as the aspect ratio of a rectangle. The aspect ratio illustrates the proportion of time for a fluid to flow in vertical and horizontal axes of the reservoir, when the equal pressure difference is employed. The determination of flow regime in the advanced part of the investigation is performed by the help of this explanation. It is important to express the vertical scale along with the horizontal scale on a stratigraphic cross section to indicate significant details of stratigraphic variation or dip angle of a reservoir. It is imperative to understand the effect that this distortion has on reservoir area or geometry and angular relationships of formation surfaces. The small angular differences among stratigraphic horizons that can consider for thickness variations are strongly exaggerated in such a section.

4. Scaling classification

Based on the principles on which the scaling criteria are developed, they can be categorized as (a) Scaling criteria based on flow and fluid properties, (b) Scaling criteria based on displacement techniques and (c) Scaling criteria based on reservoir geometry. This review article will focus on these three types of scaling principles.

4.1. Flow and fluid properties

This type of scaling principles should be established depending on the fluid/reservoir interaction. It can distinguish wide-ranging flow performance which include equilibrium of capillary, gravity and viscous forces. The flow properties should also be considered for these forces which present the consequence of extrapolation from the initial scale to the scale of concern.

4.1.1. Multi-phase flow

The use of miscible and immiscible multiphase flow scaling has been investigated previously for different EOR techniques. Leverett et al. (1942)studied the dimensionless scaling numbers for immiscible water induced oil displacement process. The effect of water/oil viscosity ratio on immiscible displacement was studied by Croes and Schwarz (1955). The results found for linear displacement of oil by water is presented in the form of diagram for similar formations. The effect of gravity separation of five spot models for miscible and immiscible displacement was presented by Craig et al. (1957). It is difficult to build bridges between theoretical multiphase flow behavior and field applications for a hydrocarbon reservoir without simplifying assumptions which result in questionable conclusions (Rapoport, 1955). Rapoport developed the scaling laws for water-oil displacement process for an incompressible, immiscible and two-phase flow system. Scaling groups including capillary and gravity number has been derived by inspectional analysis. Difficulties have been raised, when reproducing identical capillary pressure and similar relative permeability curves. The different types of model tests performed with different materials can study the water flooding process for a broad range of reservoir settings. In turn, for a specific reservoir, its behavior could be evaluated by interpolating its characteristics into the ranges covered by the scaled model studies. In contrast, Grattoni et al. (2001) described a succession of trials regarding the impacts of water saturation and wettability on multi-phase flow. They exceptionally considered the gravity-dominated environments of gas injection. The trials were conducted by instinctive gas injection and dispersion of oil in bead-pack models at very high and low water saturations. Different recovery rates of oil had been found. The procedure seemed to be less effective at irreducible water saturation for the case of oil-wet condition. Similar recoveries were monitored at residual oil saturation in both cases of water and oil wet condition, respectively. The authors found a straightline connection between the derived dimensionless group and all the analyzed conditions of overall recovery. Suzuki and Hewett (2002) demonstrated an innovative technique to scale up the multi-phase flow properties. It ultimately represented the proper boundary conditions in the upscale section. They depicted a technique to scale-up an entire finely-gridded model and decide the boundary conditions using injection tubes for two phase flow. This novel technique can correctly capture the fine-scale two-phase flow behavior, such as saturation distributions, inside each segregated coarse-grid domain. They presented that this method can be pertinent to both viscosity dominated and gravity affected flows for reasonable gravity to viscous ratios. Later, Azoug and Tiab (2004) developed a comprehensive approach using the pseudo function for upscaling three dimensional anisotropic heterogeneous reservoirs. It was considered for multiphase flow with different capillary and gravity numbers. They compared the performance of several pseudo function techniques by considering diverse flow regimes. These are represented by different types of homogeneous small grid models. The researchers became successful to reproduce the oil production level and water cut of fine grid for equilibrium, viscous dominated and capillary controlled flows. On the other hand, the authors were unable to match the curves of fine grid using pseudo function techniques for the gravity controlled flow. Finally, they became successful in upscaling small to large grid simulation for high flow rates using pseudo functions.

4.1.2. Two-phase flow

Artus and Noetinger (2004) reviewed the main upscaling techniques to derive different capillary and gravity numbers for heterogeneous reservoirs in terms of two-phase flow. They investigated numerical fine to coarse grid methods. Additional physical methods were employed where the statistical arrangement of transport equations was emphasized. They showed a comprehensive logical and numerical study of the dynamic contrast of oil-water front through the study of viscous connection between the pressure and saturation. There was an extremely effective communication found between the steady or unsteady statecharacter of the fluid flow displacement and heterogeneity of the reservoir. The connection of this type is reliant on a subjective and measurable alteration of the extensive scale conditions. It must be represented by any upscaling procedure. Later Zhang et al. (2005) demonstrated how conventional upscaling methods may deliver erroneous results and suggested a simple alternative. They reproduced single phase flow and greatly increased the coarse-scale two phase flow model using suitable boundary conditions. This method is slower than the local upscaling method and cannot consider the physical disruption caused by heterogeneity in the fine-scaled model. It is not suitable for small scale heterogeneities where capillary pressure has a significant impact on the fluid flow. Pfister and Chanson (2014) summarized the water-air interfacial properties and the air entrainment rate under a Froude similitude. It represents the physical background of a pore physical model. The smallest values of Weber or Reynolds numbers were considered to limit the scale effects. Based on a literature review, they presented and discussed the existing limit, bringing about a progression of more moderate recommendations in terms of air concentration scaling. As the selection of criteria to examine the scale effects was crucial, it was observed that a couple of factors (e.g., bubble sizes, turbulent scales etc.) can be influenced by scale consequences, even in comparatively large laboratory models.

4.1.3. Capillary to viscous force

Hilfer and Øren (1996) reexamined the multiphase flow equations of small and large scale in porous media through the traditional dimensional analysis. Depending on the category of length scale, porous medium and saturation history, a macroscopic capillary number was presented that differs from a microscopic capillary number. The macroscopic number could be associated with the Leverett J-function. The microscopic number is the ratio of viscous pressure drop to capillary pressure. The sample calculations of desaturationcurves are provided when the macroscopic number is equal or close to one for distinctive porous media. Finally, the analytical modification between residual oil saturation of laboratory experiments and field implementations were provided. On the other hand, Wibowo et al. (2004) studied the impact of the forces correlation in horizontal well production operation for bottom water drive reservoirs. They successfully constructed a scaled physical model. It can be simulated in the production operation using dimensional analysis and showed that the linking of the reservoir forces increased as the proportion of gravity to viscous forces increases. The significant finding of their work was the well production performance of the reservoir. It will enhance as the capillary pressure is decreasing, and subsequently the increase of gravity to viscous force ratio will improve the oil recovery. Later, Jonoud and Jackson (2008) showed the capillary or viscous forces flow which validate the steady-state scaling techniques. They found that reservoir flow rates within a reasonable range were valid for viscous limit upscaling techniques. The capillary equilibrium limit technique was limited to exceptionally reduced rates, because it overestimates the amount of capillary entrapping. However, the authenticity of capillary equilibrium limit upscaling in a 3D model was not properly captured.

4.1.4. Fluid saturation and relative permeability

Perkins and Collins (1960) redefined the relative permeabilities and fluid saturations. Their definition permits one to have diverse relative permeability and capillary pressure relationships in the prototype and model. This work proposed a method to authorize a diverse relationship between relative permeability and fluid saturation with capillary pressure. This relationship helps to derive the modified capillary number. They demonstrated one simple example that clarifies how to derive modified scaling criteria. Astarita (1997)discussed the modern viewpoint of dimensional analysis. It is the basis of the theory of scaling to derive gravity and capillary number. The author illustrated several specific examples to show how scaling and dimensional analysis may generate actual important point for the solution of the problem. Finally, the author showed that using scaling, dimensional analysis and the estimation of the order of magnitude can be used to derive those dimensionless group. Durlofsky (1998) developed a coarse scale equation using a volume average saturation calculation of small scale in dissimilar reservoirs. It can be used for two phase flow to evaluate several approaches for the detailed upscaling method for reservoir characterization. The author discussed the strengths and limitations of each of these techniques. Especially the fundamental assumptions in those calculations using the volume-averaged equations as a framework equations. These equations were rearranged for the unit mobility ratio case and applied to the immediate solution of a coarse scale model issue. Wang et al. (2009) demonstrated the large error behind the conventional upscaling method. They established a novel approach for the upscaling method of the relative permeability curve. A large model upscaling method was used which best fits with the fine scaled model. The authors verified this method by constructing a three-dimensional, three-phase and extremely dissimilar reservoir model. As contrasted with the conventional method the new coarse scaled upscaling method demonstrated a more reasonable result. The outcome can be attained by approximating the consequence of ambiguity through computational time, order and magnitudes quicker than the earlier methods. Tsakiroglou (2012) developed a model using a network type multi-scale analysis for immiscible displacement of both wetting and non-wetting phase fluid in dissimilar porous media. The author utilized these methods to decide the transient consequences of the axial dispersion of water saturation, pressure drop. Finally, the functions of relative permeability can be evaluated with its upscaled impact.

4.1.5. Rock and fluid memory

Hossain and Islam (2011) developed new scaling criteria incorporating memory concept using inspectional and dimensional analysis. They became successful to develop relationships between capillary pressure, saturation, velocities and fluid pressure for prototype and model. The authors identified a competent tactic for oil-water displacement process by deriving the sets of similitude groups. Hossain and Abu-Khamsin (2012a) developed new dimensionless groups using mathematical modeling of non-linear energy balance equations. The developed numbers were helpful to demonstrate the rheological behaviorof fluid-rock interactions. Their proposed dimensionless numbers described the various types of heat transport mechanisms including convection and conduction in porous media for the processes of thermal recovery. These dimensionless numbers were found to be responsive to a large set of fluid and reservoir rock properties including densities, permeability, heat capacities, porosity, etc. Hossain and Abu-Khamsin (2012b) also developed new dimensionless numbers which can describe convective heat transfer between the fluid and rocks in continuously changing conditions using the memory concept. They employed an energy balance equation to develop the heat transfer coefficient by assuming the rock can attain the temperature of the fluid immediately. The developed new numbers correlate with the Nusselt and Prandtl numbers and the local Peclet number is observed to be responsive to memory.

4.1.6. Spontaneous imbibition

Mirzaei-Paiaman and Masihi (2013) developed scaling equations utilizing counter-current spontaneous imbibition method for oil and gas recovery from fractured porous media. Earlier scaling equations were defined systematically by linking the primary time squared recovery to squared pore volume. They showed that this settlement does not employ to general scaling performances and, if employed, it affects nontrivial sprinkle in the scaling designs. The authors proposed that throughout the expansion of any scaling equations, its reliability with mutual purposes should be measure which was neglected in the literature. The authors have rewritten scaling equations for two physically expressive numbers, namely, the Darcy number and the Capillary number. It was authenticated by the investigation data from the literature. The authors scale up available data in an efficient way and represented different recovery curves by a single master curve.

4.1.7. Compositional flow simulation

Li and Durlofsky (2015) developed an upscaling procedure which is more precise and robust for the simulation of flow composition. They computed the functions related to coarse-scale boundary or block and the prerequisite upscaled factors by using a technique. This technique requires a global fine-scale compositional simulation. The authors introduced near-well behaviors along with a technique for enhancing the α-factors for both production and injection wells. It was combined further to upgrade the coarse-model appropriateness. Finally, they suggested that using their technique the produced upscaled models can be employed to lessen computational difficulties for different purposes including the optimization of well control.

4.2. Displacement techniques with initial and boundary conditions

Different type of scaling groups is derived depending on various displacement techniques along with their initial and boundary conditions. Major scaling groups derived using this technique are the dimensionless time and displacement efficiency factor. These scaling groups will represent the dimensionless production response of a reservoir. The development of scaling criteria is subdivided in the following sub-sections depending on different displacement techniques.

4.2.1. Immiscible displacements

Rojas (1985) performed scaled model studies for immiscible CO2 flooding of substantial oil. Lozada and Ali (1987) displayed a group of scaling criteria including six groups of scaling processes. They concluded that a full set of scaling criteria might not be fulfilled at the same time. Thus, few groups had to be excluded to fulfill the major scaling conditions, including the vital factors of a specific method. The authors found that the nature of fluid/rock schemes, flow rate, pressure drop, model geometry and so forth were dissimilar contingent upon the methods exercised. Later, Lozada and Ali (1988) also developed partial differential equations of immiscible carbon dioxide flooding for the moderately heavy oil reservoir. The authors used different sets of scaling criteria to construct scaled models with different operating conditions. A series of similitude numbers was derived for the displacements of moderately heavy oil recovery by dimensional and inspectional analyses. The mass transfer between the phases were considered for immiscible carbon dioxide flooding. So, all the similarity groups were not satisfied in the case of recovery from moderately heavy oil reservoirs. They relaxed some of the groups which had less effect on the physical mechanism and hence found out the dominant scaling groups. Peters et al. (1993) studied the saturation data through a dimensionless self-similitude parameter to develop the dimensionless representative response curve for variable core floods. The authors found that there is a considerable dissimilarity between the response function of oil wet to water wet reservoir. Finally, the results showed that the effectiveness of displacement could occur in water wet reservoir compared to oil wet reservoir. Zhou et al. (1997) defined three dimensionless groups, namely, gravity viscous ratio, shape factor and viscous capillary ratio. These dimensionless numbers help to detect influential flow regions at numerous situations. They demonstrated the comparative extents of energies in the scheme linked through the reservoir properties. The scaling groups and flow areas governing different kinds of flow performance inthe schemes were examined with straightforward heterogeneity formulae. The authors considered three frequently used flow schemes such as immiscible displacement with layered reservoir in homogeneous media, miscible displacements in layered reservoir without scattering and fluid flow in the reservoir with high fracture.

4.2.2. Controlled gravity drainage

Zendehboudi et al. (2011) performed dimensional analysis for scaling the immiscible displacements of controlled gravity drainage (CGD) method. The authors obtained an empirical model in fracture dominated porous media by dimensional analysis using Buckingham π theorem to investigate the gravity drainage process. They developed a model to forecast the maximum withdrawal rate, the distance of fluid-gas interface locations, critical pumping rate and the recovery factor of fluid experiencing the CGD methods. The developed model delivers satisfactory predictions for the oil-gas drainage system.

4.2.3. Immiscible GAGD process

Sharma and Rao (2008) developed a scaled physical model of the gas-assisted gravity drainage (GAGD) technique to describe the enhanced recovery method. They determined the impact of a few dimensionless scaled factors. For example, the Gravity number, Bond number and Capillary number effect on GAGD technique implementation. Sharma and Rao (2008) found that the Bond number significantly affects GAGD performance than any other numbers. Finally, they relate the run time of the model to the run time of field development to observe high recoveries. Dimensionless time indicated augmented rate of recovery when GAGD method is implemented in field projects. Farahi et al. (2014) developed a few scaling groups by performing inspectional analysis. These groups had analyzed the performance of reservoir fluid displacements by immiscible GAGD technique. They determined five matched scaling groups for homogeneous reservoirs. The authors found a coefficient for different reservoir which is called the coefficient of Dykstra-Parson. They determined another new set of dimensionless groups in large scale that added altogether the prevailing energies. Finally, they evaluated and verified experimental results and found it consistent for rapid forecast of oil recovery for GAGD technique.

4.2.4. Miscible displacements

Gharbi et al. (1998) studied the miscible displacement scaling in permeable medium utilizing inspectional investigation to produce scaling sets. These sets influence displacement method in a 2D, similar, different cross-sectional formation. They derived nine groups of dimensionless numbers and from which only one number was found to have no impact on this displacement technique. Babadagli (2008) determined dimensionless scaling groups for miscible displacement utilizing inspectional analysis in a fractured porous and permeable medium. They proposed a new dimensionless number based on the dimensionless group they derived for better characterizing the efficiency of the method. The proposed new group which is called Matrix-Fracture Diffusion Number (NM-FD) was significant in assessing the efficiency of CO2 sequestration, enhanced oil recovery, and pollutant transportation issues. The authors performed validated laboratory scale experiments, and physically interpreted the Matrix-Fracture Diffusion Number (NM-FD).

4.2.5. Water flooding

Carpenter et al. (1962) represented the outcomes of model analyses of water-oil displacements with water flooding scaling relationships in heterogeneous reservoirs with vertical communicating strata of different permeability. They showed the combined influence of viscous, gravitational and capillary forces on water-oil recovery behavior. The study was performed in a water-wet system where strong imbibition forces were present. The outcome of the study showed that these relationships can be successfully applied to the water flooding process. Finally, they found the effects of capillary imbibition would be varying for different wettability. Bai et al. (2005) determined a full group of scaling conditions of five-spotted pattern wells for water flooding reservoirs. They used three dimensional governing equations for this, including capillary and gravitational force along with oil, water, and rock compressibility. The authors estimated the impact of individual dimensionless factor on investigation outcomes using this approach. They sorted out the dominant scaling numbers with larger sensitivity factors ranging from 10−4 to 100. Jin et al. (2009)developed dimensionless numbers using inspectional analysis for bottom water drive reservoir. They provided the procedure and technique involved in developing the dimensionless numbers. The description of the steps involved in deriving the groups and the problems associated with these groups had also discussed. Finally, the authors validated these groups from the sensitivity analysis of reservoir-well system without changing the values of involved parameters.

4.2.6. CO2 flooding

Prosper and Ali (1991) presented a recovery mechanism comprising a two-dimensional and linear scaled model for the water-alternating-gas (WAG) and the low pressure immiscible carbon dioxide flooding. They compared the results of the Aberfeldi field using the same model at the same pressure and WAG ratios. The authors found the oil recovery of model involving linear analyses was about one half at 2.5 MPa pressure. The bottom recovery involving waterflood was 40% and the incremental recovery of 10% was due to the WAG process. On the other hand, the recovery for the two-dimensional model varied from 40% to 50%. Bansal and Islam (1994) performed a study of sequential scaled model by injecting carbon dioxide, propane and nitrogen gas in the reservoir. The gas injection is a principal method for the recovery of heavy oil reservoir in Alaska. Nearly 65% of oil initially in place is recovered; the same is indicated by their experimental outcome. For gravity drainage, although the final recovery was the same, it took longer time to recover the same amount of oil. They found the recovery mechanism was different for different gases and the highest recovery was obtained with carbon dioxide. Viscous fingering takes place with different degree of severity when applying different gas flooding techniques. It is considered harmless as the ultimate recovery is higher by gas injection.

4.2.7. Steam flooding

Pujol and Boberg (1972) presented different approaches for scaling the investigation of stream flooding process in viscous oil reservoirs. The scaling of capillary pressure was not considered essential to represent highly viscous oils. On the other hand, for intermediate viscosity oil (less than 10,000 cP), unscaled capillary pressures can predict the optimistic recovery of oil. They developed a method to convert capillary pressure into the scale, and discovered that it can give qualitative enhancement as the recovery of oil is sensitive to flooding rates. The authors found oil recovery was mainly dependent on per unit volume of heat input to the formation. Kimber et al. (1988) developed novel dimensionless scaling numbers for the recovery of oil by steam or a steam improver and discussed their relative merits. They determined a group of similitude numbers which allow the utilization of similar fluid in prototype and model through inspectional and dimensional analyses. The authors also compared their approach with other approaches which were published in the literature and discussed their relative merits. They outlined a means of developing or selecting a process that best fits the most important characteristics of a specific recovery scheme. Doan et al. (1990) presented mathematical models to derive dimensionless scaling groups of flow inside the horizontal wellbore for performing laboratory investigations. They used variable diameters of horizontal wellbore, and skin factors to conduct the experiments. They carried out a series of steam injection experiments through a development well. Pressure behavior and temperature distribution were controlled to explain the recoveries of oil. They evaluated oil recovery performance for various types of experiments to determine the effectiveness of different horizontal wells and the impact of perforated casing. Doan et al. (1997) performed steamflood tests utilizing a physical model of the Aberfeldy reservoir (Saskatchewan) to scale up and inspect the recovery of the steamflood technique for horizontal injection and production wells. They analyzed the results from two types of experiments: a base case run steamflooding of homogeneous reservoir and a reservoir having 20% net pay bottom water layer. They presented scaling up laboratory outcomes to predict the performance of a prototype. The diagnostic heat loss model demonstrated a 3.1% difference from experimental results. Scaled-up test information data for a base case run showed that approximately 20% of the oil initially in place was recovered after 0.8 PV of steam added. For a reservoir having 20% net pay, the increase in the oil recovery depends on how the energy contained in the fluid is managed.

4.2.8. Hot fluid injection

Willman et al. (1961) assessed the outcomes of laboratory investigations for steam, cold water and hot water injection. They studied different cell measurements with various permeabilities. The authors found cold water drive had less recovery than hot water and steam injection drive. Finally, they found the soaked steam with high temperature and pressure is more effective in terms of recovery than steam with low pressure. Moreover, all types of recovery have greatly improved if the temperature of the injected fluid is higher. Cheng and Cheng (2004) provided a fundamental idea of dimensional analysis scaling and reviewed the present research employing these ideas to model the quantities of instrumented indentation. They analyzed the indentation of pyramidal and conical shaping in various viscoelastic materials. They likewise indicated scaling approaches which were best fit for these processes and provide a superior understanding of instrumented indentation measurements. Heron et al. (2005)developed thermally improved remediation techniques which were favorable for the elimination of pollutants at intensely polluted places. They developed methods to incorporate invasion of hot air, high temperature steam or water using thermal wells or heat blankets; electrical heating with low frequency; microwave heating; etc. These techniques are also described by Hinchee and Smith, 1992, Heron et al., 1998 and Davis (1997).

4.2.9. Solvent/chemical injection

Geertsma et al. (1956) extended the scaling theory to hot water drive and solvent injection by utilizing dimensional and inspectional analyses. They assumed uniform porosity and isotropic permeability. Since not all the scaling groups can be considered in building a model, a comprehensive discussion on which scaling groups are negligible were provided. Nonetheless, experimental studies were performed to verify the feasibility of neglecting some scaling groups. Sundaram and Islam (1994) presented a scaled physical model of petroleum pollutant removal using solutions of surfactants. They developed scaling principles for the decontamination process where viscous forces, aquifer geometry, and the proportion of the viscous to gravitational forces were used. Experiments were conducted to examine the type and concentration of surfactants and injection/production strategies. They found optimum surfactant concentration needed for the removal of a specific contaminant with surface tension. The outcomes of experiments showed that using this decontamination technique more than 90% of the contaminant originally in place may be removed. Basu and Islam (2009) performed a sequence of chemical adsorptionexperiments to provide most influential scale up form. The authors contrasted their outcomes with numerical simulation results. The numerical solutions were offered based on flow rates of the fluid, pore velocity, the amount of adsorbent used and the adsorption coefficient which were related to field environments. Finally, they developed a guideline to interpret the investigational outcomes and applied the scaling laws to forecast the field performance. Veedu et al. (2010) presented an upscaling methodology for chemical flooding by comparing results between coarse and fine grid method. Their technique was quite dissimilar than the other upscaling methods used for EOR process. They showed that for a heterogeneous reservoir the salinity gradient was not effectively picked up by the coarse grid method. It can lead to lower recovery than the simulations of the fine grid method. Finally, they recommended to use fine grid upscaling for better performance prediction of chemical flooding.

4.2.10. Polymer flooding

Islam and Ali (1989) obtained new dimensionless scaling groups which can incorporate the flow of foams, emulsions and polymers. They focused on the significance of mass transfer among phases, fractional flow, diffusion, adsorption, trapping, slug size and interfacial tension. New groups of scaling conditions were derived for co-surfactant improved polymer flooding with a mathematical explanation. The relative permeability and interfacial tension model were also obtained by Islam and Ali (1990). Bai et al. (2008) developed a group of scaling principles by taking into consideration many factors for polymer flooding in the reservoirs. They evaluated the sensitivity analysis of each of the dimensionless numbers. A numerical approach was recommended to enumerate the sensitivity analysis of every dimensionless number. The researcher analyzed the influence of specific physical parameters, such as injection rate, oil viscosity and permeability, on the predominant level of the dimensionless numbers. Finally, they determined the leading ones for distinctive circumstances. Guo et al. (2012) identified the dimensionless leading scaling groups in heavy oil reservoirs for polymer flooding. They derived twenty-eight dimensionless scaling numbers and build up a mathematical model to authenticate the efficacy of these scaling numbers. The authors performed numerical sensitivity analysis of individual scaling numbers to find out their consequences on the recovery of oil. They identified nine dominant scaling numbers which were used to design field scale oil recovery experiments.

4.2.11. Micellar flooding

Thomas et al. (1997) discussed the design of micellar flooding experiments using scaling laws. They derived scaling criteria utilizing dimensional and inspectional analyses with six elements for three-phase flow. These criteria were derived in several ways. The partial differential equations, constitutive relations and initial and boundary conditions are used to form a mathematical model. Finally, the mathematical model was simplified and a group of scaling principles was derived which was applicable to most laboratory conditions.