A review on simulation of methane production from gas hydrate reservoirs: Molecular dynamics prospective

1. Introduction

Sir Humphry Davy discovered the hydrate in 1810. He observed that a crystalline solid was created by an aqueous solution of chlorine when it was cooled. Then, in early 1820, John Faraday conducted some experiments that confirmed the Davy's results. However, it remained a matter of “academic” enthusiasm, until Hammerschmidt (1934) claimed in 1934 that hydrates (as the main reason) are responsible for obstruction of gas and oil transportation in pipeline systems. Since then, the hydrate inhibition methods have been persistently tested through various research activities by scientists across the world (Wu et al., 2007, Huo et al., 2001, Seo and Kang, 2012, Lee and Englezos, 2006, Fair, 1967, Urdahl et al., 2003, Gengliang, 2004). In this field of research, apart from the gas hydrate formation conditions, the impacts of inhibitors on the equilibrium conditions have been widely studied. The soaring cost of hydrate inhibition has been one of the important concerns in the gas and oil energy sectors since 1970.

Gas hydrates are solid ice-like substances formed from water when the natural gas (e.g., mainly methane) combines with water under high-pressure and low-temperature conditions. As the gas hydrates contain a vast quantity of methane gas and globally occur in profound water and permafrost areas, they can provide a viable (and additional) energy resource (Collett et al., 2009). Natural gas hydrates (NGHs) are non-stoichiometric compounds which are made of water molecules at particular thermodynamic conditions, depending on the temperature, pressure, and composition. Each standard cubic meter of NGH can result in approximately 160–180 cubic meters of natural gas under normal conditions (Sloan and Koh, 2007).

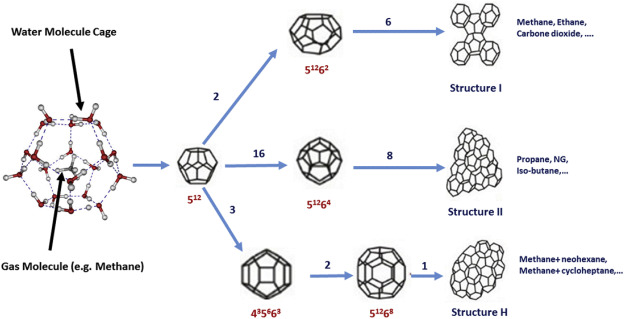
The best conditions required for gas hydrate formation are usually low temperatures (<300 K) and high pressures (>0.6 MPa) (Sloan, 1998, Sloan, 2003). Hydrate structures are classified into three categories, depending on the size of guest molecules, and type and number of cavities that cause water molecules to change their arrangements. These three common structures are called structure (type) I (Pauling and Marsh, 1952), structure (type) II (Claussen, 1951), and structure (type) H (Ripmeester et al., 1987). The most significant structural differences between various classes of hydrates are summarized in Table 1. The unit cell of structure I hydrates includes two types of cavities; namely, two small pentagonal cavities known as dodecahedrons (512), and six larger cavities which are named tetrakaidecahedron (51262) (Khan, 2001). Table 1 demonstrates that the small cavity is approximately spherical, due to a low amount of change in the radius of 3.95 and 3.91 Å in types I and II of hydrates, respectively (Sloan, 2003). The structure I of hydrates is usually created by one guest molecule such as carbon dioxide, ethane, and methane. A unit cell of structure II comprises 136 water molecules which include 16 small cavities (512) and 8 large cavities (51262) (Wu, 1994). Structure H contains small, large, and 435663 cages. The formation of structure H hydrates requires two molecules; including, a large organic guest molecule (such as neohexane), and a help gas (such as methane) (Shin et al., 2012). Fig. 1 displays the detailed information on the hydrate crystal cell structures. In all types of hydrates, maximum one guest molecule generally can be resided in each cage. Even for severe cases (e.g., extremely high pressures), there is a possibility of having multiple-cage occupancies, with uncommon small guests like hydrogen or/and xenon (Sloan, 2003).

Table 1. Parameters of three popular hydrate structures (modified after reference (Sloan, 2003)).

Hydrate crystal structure	I		II		H
Crystal type	Cubic		Cubic		Hexagonal
Space group	Pm3n (no. 223)		Fd3m (no. 227)		P6/mmm (no. 191)
Lattice parameter	α = 12 Å α = β = γ = 90°		α = 17.3 Å α = β = γ = 90°		α = 12.2 Å, ϲ = 10.1 Å α = β = 90°, γ = 120°
Number of waters per unit cell	46		136		34
Cavity	Small	Large	Small	Large	Small	Medium	Large
Number of cavities per unit cell	2	6	16	8	3	2	1
Average cavity radius (Å)	3.95	4.33	3.91	4.73	3.91	4.06	5.71
Coordination number	20	24	20	28	20	36

More than 27 percent of the land (e.g., mainly freezing rocks) and 90 percent of the sea have the potential to contain gas hydrate reserves (Kvenvolden, 1998). Moreover, the changes of pressure and temperature in longer distance especially in pipeline systems are more favorable conditions for hydrate formation. Therefore, it is vital to offer an economical, effective, and safe operation in the gas and oil production sites. Generally, the phase equilibriumof a gas hydrate is investigated through various operational strategies such as depressurising and thermal stimulation. According to this approach, the exploitation procedures of a gas hydrate can be arranged as depressurisation, thermal stimulation, chemical injection, and gas swapping (Burshears et al., 1986). Recent studies illustrate that the depressurisation method (when the pressure of the deposit is decreased to a value lower than the dissociation pressure at the dominant temperature) is the most promising technique for hydrate dissociation (Demirbas, 2010, Kurihara et al., 2008, Moridis, 2002, Liu et al., 2008). Although the hydrate formation and decomposition conditions have been investigated by some researchers at various conditions, further experimental and theoretical studies on the hydrate kinetics and gas hydrate decomposition should be carried out to understand the phenomenon mechanisms. For instance, the hydrate formation and decomposition have been studied by researchers to investigate a variety of key aspects such as synthetic seawater calculation, formation and decomposition kinetics of hydrates in different solutions (e.g., ionic and non-ionic liquids), decomposition enthalpies, formation conditions for the refrigerants in aqueous solutions, gas consumption in formations, and induction time in the bentonite clay suspension systems (Kakati et al., 2015, Kondori et al., 2013, Saw et al., 2012, Nazari et al., 2013, Saw et al., 2014, Ngema et al., 2016a, Saw et al., 2013).

Molecular dynamics (MD) is an interesting and efficient computer simulation method. A deep understanding of microscopic mechanisms can be achieved through MD simulations. MD simulation technique has been proven as a powerful research tool to analyze the behaviour of complex systems so that it gives information on structural and dynamical properties at the molecular level. It involves solving the classical equations of motion in the system. MD simulation studies of NGH have evolved during the past years (Moon et al., 2003, Zhang et al., 2008, Freer and Sloan, 2000, Storr et al., 2004).

The present work focuses on important aspects (e.g., hydrate dissociation, and methane production) of gas hydrate reservoirs which have been highlighted in the literature over recent years. In fact, it provides a brief review of hydrate dissociation under depressurisation, thermal stimulation, inhibitor injection, and gas swapping. In addition, the article investigates the various features of molecular dynamics simulations including main governing equations, assumptions, and potential functions concerning the decomposition of methane hydrate.

2. Gas hydrate reservoirs

Global energy demand is continuing to rise. There has been an increased interest in hydrates as an energy source, because gas hydrates are more available than other resources in the world and many governments/countries can benefit from them. In addition, the production cost for hydrate reservoirs is only 10–20% more than the cost for the standard (conventional) natural gas production technologies (Makogon et al., 2007). Knowing the fact that in the late 21st century there will be a sharply decline in hydrocarbon resourcesbecause of the human population growth, hydrate reservoirs seem to be a promising energy resource in the near future. Hydrates can be considered as a huge source of natural gas, because one cubic foot of solid gas hydrates contains an amount of gas which is 150–170 times higher, compared to one cubic foot of the corresponding natural gas at the standard conditions (Gudmundsson et al., 1994). Hence, by altering gas to the hydrate, a massive volume of gas can be stored under special temperature and pressure conditions (Masoudi and Tohidi, 2005).

The volume of gas hydrates and types, elastic, and petrophysical properties of the sediments/rocks appear to be vital to describe gas hydrate reservoirs (Holbrook et al., 1996). Holbrook et al. (1996) showed that the lower limit of gas hydrate stability (e.g., bottom-simulating reflector, BSR) is found in about 450 m below the seafloor (mbsf). There are diagenetic carbonates as nodules and lamina in upper and lower limits of the BSR without the mineralogical or sedimentological interruption. The mineralogy and composition of these diagenetic carbonates in equilibrium state should be used to determine the formation conditions of gas hydrates (Pierre et al., 2000). In the Blake Ridge, the thickness of diagenetic carbonate sediments (nodules or/and laminae) has been reported to be within the range of 1–10 mm (Paull et al., 1996). In addition, there are some small cubic crystals of sulfide components such as pyrite. Pierre et al. utilized scanning electron microscopy (SEM) and transmission electron microscopy (TEM) tests to characterize the crystals of smear slides (Pierre et al., 2000). Based on the tests results, they observed that the hexagonal structures in the forms of single, twinned, and aggregated crystals are smaller than 1 μm (Pierre et al., 2000). Kvenvolden et al. (Brewer et al., 1998) conducted a research work on the oxygen isotopic compositions of the diagenetic carbonates. They demonstrated that the gas hydrates formation occurs in the BSR upper limit of all sedimentary sections.

According to the geophysical methods, it has been proved that methane hydrates are available throughout the world's oceans, primarily on the continental shelves (Fig. 2) (Pinero et al., 2013). Fig. 2 demonstrates that the minimum amount of gas hydrate sources (10 kg/m2) is normally found in the extended border zones. The estimation of global hydrate resources has been published by many scientists (Dobrynin et al., 1981, Makogon, 1981a, Harvey and Huang, 1995, Holbrook et al., 1997, Johnson, 2011). According to the literature, the deposits of hydrates in both shale and sand formations have an economic potential. Although there is a high likelihood of hydrates in the porous systems with high porosity and permeability, hydrate production in marine and arctic sediments have always attracted attention of industrial and academic sectors in terms of technical, economic, and environmental prospects (Johnson, 2011). For example, Makogon (1966) introduced a methodology to calculate the amount of subsurface gas hydrates. In another work, Kvenvolden (1999) discussed about all estimations of gas hydrate resources. This research study predicted 21 × 1015 m3 methane in the hydrate sources (Kvenvolden, 1999, Wood et al., 2002, Hesse, 2003). The maximum amount of gas hydrates (above 100 kg/m2) is also located in the continental margins of Alaska, Peru, Japan, Chile, Argentina, Indonesia, Taiwan, and Gulf of Oman (up to 157 kg/m2stored gas hydrate) (Pinero et al., 2013). The gas hydrate reservoirs are considered as a huge energy source, compared to other hydrocarbon reserves(Fig. 3) (Pinero et al., 2013). The gas hydrate inventory varies considerably according to various reports in the literature; nonetheless, the amount is still very large. (Hester and Brewer, 2009).

2.1. Classification of methane hydrate reservoirs

There are three main classes of gas hydrate reservoirs in terms of geological characteristics, thermodynamic behaviors, and production strategies (Fig. 4) (Moridis and Collett, 2003, Kurihara et al., 2011). Class 1 reservoirs are made of a hydrate-bearing layer and an underlying two-phase zone which contains liquid water and gas. Class 1 (Fig. 4a) reservoirs are also called hydrate-capped gas reservoirs (Gerami and Pooladi-Darvish, 2006). The hydrate, liquid, and gas are in equilibrium. This class of reservoirs can be divided into two categories based on the presence of components in the hydrate zone: hydrate and gas (Category 1G) and hydrate and water (Category 1W) (Moridis, 2008). Class 2 reservoirs are composed of a hydrate-bearing interval with an underlying water-zone where the free gas is absent (Fig. 4b). As all components in hydrate layer have the same temperature and pressure (i.e., thermodynamic equilibrium conditions) and there is no free gas in the multi-component system, the amount of produced gas and production rate are very low in this kind of gas hydrate reservoirs (Moridis, 2008). Class 3 includes a single hydrate-bearing zone. This type of gas hydrate reservoirs (e.g., Class 2) experiences the slow production rates during the decomposition process as the temperature and pressure conditions fall in the stability region (Fig. 4c) (Moridis and Reagan, 2007).

Among three different decomposition methods, the depressurisation is appropriate for all classes of the hydrate reservoirs as this technique is simple, cheap, and fast. The fast alteration of pressure and temperature might lead to the secondary hydrate formation in gas reservoirs (Moridis and Reagan, 2007, Kurihara et al., 2005, Hong et al., 2003). Hence, the warm water injection (e.g., thermal stimulation method) near the well can be efficient to destroy the new hydrates (and ice) and lower the possibility of well chocking.

2.2. Hydrate decomposition kinetics

The production of hydrate methane means decomposing methane hydrate in the reservoirs and collecting the resultant methane gas in wells and downstream facilities. The kinetics of hydrate decomposition has been investigated for a few systems. Yin et al. (2016) discussed about 14 different kinetic models of hydrate dissociation. The most important models since 1980s are presented in Table 2. The models are divided into three different types based on the solution method; namely, analytical, numerical, and empirical methodologies (Yin et al., 2016).

Table 2. Summary of gas hydrate dissociation kinetic models.

Researcher	Heat Transfer	Mass Transfer	System	Intrinsic Kinetics	Porous Media	Solution Method
Ullerich et al., 1987	✓	✓	Hydrate + Water + Methane Gas	–	–	Numerical
Kim et al., 1987	–	✓	Hydrate + Water + Methane Gas	✓	–	Analytical
Holder and Angert, 1982	✓	✓	Hydrate + Water + Methane Gas	–	–	Numerical
Burshears et al., 1986	✓	✓	Hydrate + Water + Mixture of Methane, Ethane and Propane	✓	–	Numerical
Selim and Sloan, 1989	✓	✓	Hydrate + Water + Methane Gas	–	✓	Analytical
Jamaluddin et al., 1989	✓	✓	Hydrate + Water + Methane Gas	✓	–	Numerical
Yousif et al., 1991a	✓	✓	Hydrate + Salted Water + Methane Gas	✓	✓	Numerical
Tsypkin, 1993	✓	✓	Hydrate + Water + Ice + Methane Gas	–	✓	Analytical
Makogon, 1981b	✓	✓	Hydrate + Water + Methane Gas	–	✓	Analytical
Khairkhah et al., 1999	✓	✓	Hydrate + Water + Methane Gas	✓	✓	Numerical
Masuda et al., 1999	✓	✓	Hydrate + Water + Methane Gas	✓	✓	Numerical
Clarke and Bishnoi, 2001	✓	✓	Hydrate + Water + Mixture of Methane and Ethane	✓	–	Numerical
Moridis, 2003	✓	✓	Hydrate + Water + Methane Gas	✓	✓	Numerical
Hong et al., 2003	✓	✓	Hydrate + Water + Methane Gas	✓	✓	Analytical
Komai et al., 2004	✓	✓	Hydrate + Water + Methane Gas	✓	–	Numerical
Ahmadi et al., 2004	✓	✓	Hydrate + Water + Natural Gas	✓	✓	Numerical
Sean et al., 2007	✓	✓	Hydrate + Water + Methane Gas	✓	–	Numerical
Nazridoust and Ahmadi, 2007	✓	✓	Hydrate + Water + Methane Gas	✓	✓	Numerical
Oyama et al., 2009	✓	✓	Hydrate + Water + Methane Gas	✓	✓	Theoretical
Gamwo and Liu, 2010	✓	✓	Hydrate + Water + Methane Gas	✓	✓	Numerical
Windmeier and Oellrich, 2013	✓	✓	Hydrate + Water + Methane Gas	✓	–	Empirical

Ullerich et al. (1987) described a numerical model without employing adjustable parameters to forecast decomposition of hydrates. This model exhibits an acceptable agreement with the experimental data. They also found that the thermal conduction poorly contributes to hydrate decomposition in the absence of sediments; however, the thermal conduction is more important in the in-situ cases of hydrate decomposition in sediments (Ullerich et al., 1987). Kim et al. (1987) suggested a method for the rate of natural gas hydrate decomposition and obtained the rate constant using the empirical data/findings for methane. Their experiments included measurement of the amount of collected methane within hydrate decomposition in a semi-batch stirred-tank reactor over an isothermal process. To calculate the intrinsic rate, the initial particle size was supposed to be constant, considering the Stokes law and settling time. In addition, it was assumed that all components have the same size before dissociation (Kim et al., 1987). Selim and Sloan (1989) introduced a mathematical model for the hydrate decomposition under thermal stimulation in porous media where heat flux and physical properties were constant. The model was based on one-dimensional semi-infinitive region, $0 < x < \infty$ . They assumed that the hydrate fills the entire pore volume and has an initial uniform temperature, $T_{i}$ . At time $t = 0$ , the temperature at $x = 0$ was increased by a constant heat flux $q_{s}$ and the temperature of the boundary was altered from $T_{i}$ to $T_{o}$ . It was also observed that the hydrate decomposition starts and the boundary surface moves to a positive x-direction $(x = X (t))$ , which separates the undecomposed hydrate region from the water/gas system. At $t > 0$ , the decomposed hydrate region occupies the zone, $0 < x < X (t)$ , while the undecomposed hydrate occupies the region, $0 < X (t) < x < \infty$ . They believed that the producing water from decomposition remains immobile and occupies the pores of the decomposed zone, and the thermophysical properties are constant. Internal effects, viscous dissipation, and possibility of external or mutual energy were ignored in their study. Having these assumptions, the differential form of the momentum balance equation is given below:(1) $φ \frac{\partial ρ_{g}}{\partial t} + \frac{\partial (ρ_{g} v_{x})}{\partial x} = 0 0 < x < X (t), t > 0$ where(2) $v_{x} = \frac{κ}{μ} \frac{\partial P}{\partial x} 0 < x < X (t), t > 0$

In the above equations, $φ$ stands for the porosity and $ρ_{g}$ and $v_{x}$ refer to the superficial gas velocity and gas density, respectively. $κ$ , $μ,$ and $P$ represent the permeability, gas viscosity, and gas pressure, respectively. The differential forms of the mass and energy balance equations are listed below:(3) $ρ_{I} C_{p_{1}} \frac{\partial T_{I}}{\partial t} + \frac{\partial}{\partial x} (ρ_{g} C_{p_{g}} v_{x} T_{I}) = k_{I} \frac{\partial^{2} T_{I}}{\partial x^{2}} + T β \frac{D P}{D t} 0 < x < X (t), t > 0$ (4) $\frac{\partial T_{I I}}{\partial t} = α_{I I} \frac{\partial^{2} T_{I I}}{\partial x^{2}} X (t) < x, t > 0$ (5) $ρ_{g} = \frac{M w P}{R T_{I}} 0 < x < X (t), t > 0$ where $T (x, t)$ is the temperature, $C_{P}$ represents the heat capacity at a constant pressure, $k$ stands for the effective thermal conductivity, $β$ represents the coefficient of thermal expansion of gas, $M w$ and $R$ are the gas molecular weight and universal gas constant, respectively. In the above equations, subscripts I and II refer to the dissociated zone and hydrate zone, respectively. The subscript g is also for the gas phase. The initial and boundary conditionsdescribing the decomposition process for the above equations are as follows:(6) ${\begin{array}{l} T_{I} = T_{I I} & x = 0, t > 0 \\ P_{I} = P_{I I} & x = 0, t > 0 \\ T_{I} = T_{I} = T_{D} & x = X (t), t > 0 \end{array}$ (7) $ω φ ρ_{H} \frac{d X}{d t} + ρ_{g} v_{x} = 0 x = X (t), t > 0$ (8) $k_{I I} \frac{\partial T_{I I}}{\partial x} - k_{I} \frac{\partial T_{I}}{\partial x} = φ ρ_{H} Δ H_{D} \frac{d X}{d t} x = X (t), t > 0$ (9) $P_{D} = \exp (A - \frac{B}{T_{D}}) x = X (t), t > 0$ (10) $T_{I I} = T_{i} x = \infty, t > 0$ (11) $T_{I I} = T_{i} 0 < x < \infty, t > 0$ (12) $X (t) = 0 t = 0$ where $ω$ and $Δ H_{D}$ represent the mass of gas produced per unit mass of hydrate and heat of dissociation, respectively. Subscripts (D) and (i) refer to the dissociation and initial conditions, respectively. Equations (7), (8) are the mass and energy balance equations at the front of the dissociation region, respectively. Thermodynamic equilibrium relationship (e.g., Antoine equation) between the gas pressure and the hydrate dissociation temperature at the dissociation interface is described by Equation (9). In Equation (9), A and B denote the component-specific constants in the Antoine equation. Selim and Sloan (1989) applied a fourth degree polynomial to approximate the exact solution in their study. The expressions for $ρ_{g} (X, T), v_{x} (x, t),$ $P (x, t), T_{I} (x, t), T_{I I} (x, t)$ , $X (t)$ , and η are given below:(13) $\frac{T_{I} - T_{0}}{T_{D} - T_{0}} = \frac{e r f (a η + b) - e r f (b)}{e r f (a ξ + b) - e r f (b)}$ (14) $\frac{T_{I} - T_{i}}{T_{D} - T_{i}} = \frac{e r f (η)}{e r f (ξ)}$ (15) $P^{2} = P_{0}^{2} + 4 \frac{ω φ (ρ_{H}) (α_{I I}) μ R}{κ M w} ξ \int_{0}^{η} T_{I} (η) d η$ (16) $X (t) = ξ \sqrt{4 α_{I I} t}$ (17) $η = \frac{x}{\sqrt{(4 α_{I I} t)}}$ in which $ξ$ is a number which depends on only physical parameters of initial and boundary conditions. Table 3 includes the magnitude of thermal, geological, and physical parameters used in Selim and Sloan (1989). They showed that the decomposition rate decreases with increasing porosity of the hydrate phase. Decomposition rate is independent of the gas viscosity and porous system permeability. It was also found that lower thermal conductivity in the hydrate region and higher thermal diffusivity in the dissociation region lead to higher decomposition rates. Through an extensive investigation, Jamaluddin et al. (1989) used two mechanistic methods (intrinsic kinetics and heat transfer) to analyze the methane hydrate dissociation. Their results showed that the rate of dissociation depends on the activation energy. It was also found that both kinetic and intrinsic rates control the dissociation rate where the system pressure and surface roughness factor change (Jamaluddin et al., 1989). Tsypkin (1993) considered two moving phase transition boundaries to construct a new decomposition model for the gas hydrate. Gas hydrate decomposed in one boundary and ice melted on the other. A high-permeable system was utilized where the dissociation in the front moved faster than the ice melting. Dissociation region was divided into three zones which were separated by two boundaries. The researcher developed a proper equation for the mass and heat transfer during the hydrate decomposition, showing the corresponding zone between the dissociation and ice melting. Khairkhah et al. (1999) concluded that an accurate estimation of gas production from hydrate reservoirs through modeling/simulation methodologies should incorporate two-phase fluid flow, kinetic rate, heat transfer, and dissociation model. Masuda et al. (1999) provided a numerical model for predicting the flow behaviour of water and gas with hydrate decomposition in a porous medium. Their results were verified with the data obtained from the methane gas hydrate decomposition in Berea sandstone cores. In addition, Clarke and Bishnoi (2001) offered a new mathematical model to calculate the intrinsic rate of gas hydrate dissociation where the gas mixtures contain methane and ethane. They performed experiments to investigate the kinetics of gas hydrate dissociation. Moridis (2003) suggested EOSHYDR2 module for calculation of gas hydrate decomposition under equilibrium for both marine and permafrost reservoirs. They used EOSHYDR2 to model gas hydrate decomposition, non-isothermal hydrate formation, transport phenomena, and phase behaviour for various hydrate cases. Moridis (Hong et al., 2003, Moridis, 2003) simulated gas hydrate decomposition of simple methane and mixture of methane and alkanes hydrates by employing exact thermochemical parameters. Hong et al. (2003)simulated gas generation from a hydrate reservoir in a porous medium by using a simple analytical model. They studied the influences of different parameters such as operating conditions, kinetic rate, and formation properties on the gas production. In addition, different equilibrium models were examined in their work. Komai et al. (2004) conducted an experimental investigation for methane hydrate decomposition below the melting point using the Raman spectroscopy. They presented a kinetic model to explain the decomposition of methane hydrate by applying non-steady state approximation diffusion-controlled regime. The governing equation used in their work was the Fick's law as expressed below (Komai et al., 2004):(18) $η \frac{\partial C}{\partial t} = D \frac{1}{r^{2}} \frac{\partial}{\partial r} (r^{2} \frac{\partial C}{\partial r})$ where D, C, and r refer to the diffusion coefficient of methane in the ice layer, concentration of methane in the hydrate, and radius of the hydrate particle, respectively. It should be noted that the mass transfer of methane occurs through the spherical wall of the ice layer. Thus, the initial and boundary conditions are as follows:(19) ${\begin{array}{l} C = C_{B} & t = 0 \\ C = C_{B} & r = r_{0}, t > 0 \\ C = C_{H} & r = X (t), t > 0 \end{array}$

Table 3. Parameters used in dislocated model (Yin et al., 2016, Selim and Sloan, 1989).

Porosity,

φ

0.3

Permeability,

κ

1.38 × 10−13 m2

Thermal Diffusion of Dissociation Zone,

α_{I}

2.89 × 10−6 m2/s

Thermal Diffusion of Hydrate Zone,

α_{I I}

6.97 × 10−7 m2/s

Thermal Conductivity of Dissociation Zone,

k_{I}

5.57 W/m.K

Thermal Conductivity of Hydrate Zone,

k_{I I}

2.73 W/m.K

Hydrate Density,

ρ_{H}

913 kg/m3

Hydrate Heat of Dissociation,

284 < T < 273

284 < T < 273

Δ H_{D} = 215.59 \times 10^{3} - 394.945 T

(J/kg)

Δ H_{D} = 446.12 \times 10^{3} - 132.638 T

(J/kg)

Antonine Equation

P_{D} = \exp (49.3185 - 9459 / T_{∖ D}

(Pa)

Gas Heat Capacity (J/kg.K)

\begin{array}{l} C_{P} = 1.23879 \times 10^{3} + 3.1303 T + \\ 7.905 \times 10^{- 4} T - 6.858 \times 10^{- 7} T^{3} \end{array}

Gas Viscosity (Pa.s)

\begin{array}{l} μ = [2.4504 \times 10^{- 3} + 2.8764 \times 10^{- 5} T + 3.279 \times 10^{- 9} T^{2} - \\ 3.7838 \times 10^{- 12} T^{3}] + [2.0891 \times 10^{- 5} ρ_{g} + 2.5127 \times 10^{- 7} ρ_{g}^{2} - \\ 5.822 \times 10^{- 10} ρ_{g}^{3} + 1.8387 \times 10^{- 13} ρ_{g}^{4}] \end{array}

In the above boundary conditions, $X (t)$ and $r_{0}$ refer to the radius of the hydrate particle (depending on the time) and the initial hydrate radius, respectively. $C_{B}$ and $C_{H}$ denote the concentration of methane in the bulk gas phase and the hydrate phase, respectively. Employing the initial and boundary conditions, the solution of the diffusion equation can be achieved in terms of the elapsed time and hydrate radius as follows:(20) $\frac{C - C_{B}}{C_{H} - C_{B}} = \frac{x (r_{0} - x)}{r (r_{0} - x)} - \frac{2 x}{π r} \sum_{n = 1}^{\infty} \frac{1}{n} \sin \frac{n π (r - x)}{r_{0} - x} exp (- \frac{n^{2} π^{2} D t}{{(r_{0} - x)}^{2}})$

They noted that the fugacity/fugacity coefficient can be calculated using a suitable thermodynamic correlation or equation of state (EOS) at different pressures. At the initial period of hydrate decomposition, it can be written $x ≅ r_{0}$ and $t ≅ 0$ . For the small interval, they assumed that the expression $ξ = \frac{(r_{0} - x)}{\sqrt{D t}}$ remains almost constant. According to this assumption, the following solution is attained:(21) $\frac{1}{2} ξ = φ [\frac{r_{0}}{x} + 2 \sum_{n = 1}^{\infty} exp (- \frac{n^{2} π^{2}}{ξ^{2}})] ≅ φ [1 + 2 \sum_{n = 1}^{\infty} exp (- \frac{n^{2} π^{2}}{ξ^{2}})]$ where(22) $ξ = \frac{(r_{0} - x)}{\sqrt{D t}}$

Using the expression $ξ$ and the relationship $I (t) ≅ {[\frac{x (t)}{r_{0}}]}^{3}$ , they calculated $I (t)$ through the following equation:(23) $\frac{{(1 - I {(t)}^{\frac{1}{3}})}^{2}}{ξ^{2}} = \frac{D t}{r_{0}^{2}}$

There is a linear relationship between $\frac{{(1 - I {(t)}^{\frac{1}{3}})}^{2}}{ξ^{2}}$ and $(t)$ based on their experiments. Their study showed that the results of diffusion-controlled dissociation regime and non-steady state approximation are in a very good agreement with the real data. It was also found that the decomposition rate of methane hydrate increases with increasing the temperature, while this rate declines as the pressure goes up. Ahmadi et al. (2004) solved the governing equation by using the finite-difference numerical technique to analyze natural gas generation from hydrate reservoirs. They forecasted the generation rate, and temperature and pressure profiles for various reservoir temperatures and well pressures. For instance, a correlation which is valid for 1-D systems was suggested for the natural gas production in gas hydrate reservoirs. Their results showed that a small alteration in temperature cannot be effective in natural gas production (Ahmadi et al., 2004). Sean et al. (2007) combined the numerical simulation outputs obtained from computational fluid dynamic (CFD) and experimental results to develop a method for determination of the intrinsic rate of gas hydrate decomposition. They showed that the boundary temperature of the methane hydrate is equal to the temperature of the ambient water. Thus, they claimed that the gas hydrate decomposition at the surface can take place at constant temperature conditions (Sean et al., 2007). Nazridoust and Ahmadi (2007) carried out a study concerning the hydrate decomposition in a porous medium by employing a computer simulation method. They used FLUENT code to simulate hydrate module for gas hydrate dissociation. Based on their research investigation, it was concluded that the FLUENT code has no capability to simulate the hydrate formation/dissociation. It was also found that the natural gas generation is a function of pressure, core permeability, and temperature. They also noticed that the temperature in the decomposition front declines due to the hydrate decomposition and after that rises because of the heat transfer. Through increasing the system temperature, the gas and water generation rates are increased. Gamwo and Liu (2010) utilized the HydrateResSim package which is a heat-flow, multi-component, and multi-flow simulation program. The model includes the equilibrium and kinetic frameworks to characterize methane generated from the gas hydrate decomposition. The simulation program can be used for four-phase flow and three-component systems to describe the methane production, as well. In addition, Windmeier et al. (Windmeier and Oellrich, 2013) conducted a theoretical study (consecutive desorption, CDM) about gas hydrate dissociation to comprehend the mechanisms of dissociation kinetics and intrinsic gas hydrate dissolution.

2.3. Gas hydrate reservoirs production methods

The production method that includes temperature rising is called “thermal stimulation” and the technique that entails the pressure reduction is called “depressurisation method”, and combination of change in temperature and pressure refers to “chemical injection”. Therefore, the operation of the “rising temperature” or “declining pressure” of layers bearing methane hydrate is the practical way of the methane hydrate production. Due to the dependency of hydrate stability on the temperature and pressure in the reservoirs, production methods are strongly affected by the P-T diagram of the reservoirs. Several conventional methods have been suggested for generation of natural gas from the hydrate reservoirs, including thermal stimulation, depressurisation, gas swapping, or/and a combination of these techniques (Sloan and Koh, 2007, Collett et al., 2015, Englezos, 1993, Makogon, 1981b, Sum et al., 2009). The alteration of temperature and pressure for three methods is shown in Fig. 5. Commercial gas generation from methane hydrate reservoirs has not been commenced yet; however, a few prosperous flow tests have been conducted in oceanic and arctic environments. The only gas generation test in a oceanic environment is the eastern Nankai Trough case on March 12–18, 2013, as a part of the research in Japan (OGMEC, 2012). The most important arctic hydrate generation test was performed at the Mallik site in the Mackenzie Delta, Northwest Territories, Canada, 2002 (Dallimore et al., 1999). Throughout a week, both thermal stimulation and depressurisation methods were employed to produce gas from the hydrates.

The most common method of hydrate dissociation is depressurisation. This method first involves lowering the pressure at the prevailing temperature inside the reservoir and facilitating the methane hydrate to be decomposed. In the thermal stimulation approaches, hot water, injected steam or/and a heated liquid (indirectly via sonic or/and electric tools) are used as a source. The other method is the chemical injection such that the chemicals are utilized to change the natural gas hydrate equilibrium conditions outside the thermodynamic states of hydrate stability zone. There are two different types of inhibitors: thermodynamic and chemical inhibitors (Sloan and Koh, 2007). Thermodynamic inhibitors with strong hydrogen bonding (like ethylene glycol and methanol) shift the equilibrium hydrate stability curve. In addition, the kinetic inhibition is able to alter the hydrate equilibrium within the hydrate stability zone, and small crystals delay the nucleation as well as the growth of gas hydrate (Sloan, 1998, Koh et al., 2002, Lederhos et al., 1996, Notz et al., 1996). There are also newly developed methods such as CO2 gas exchange through sequestration of CO2 into NGH-filled sediments (Graue et al., 2008), use of fluorine gas, and microwave technology (Arora et al., 2015). Fig. 6 depicts three different methods for methane hydrate decomposition (Marine Resources, 2014). In the first process (a), the pressure is changed by installing a pump. Due to the pressure drop, the hydrate dissociates slowly and the methane is produced. In the second method (b), methane is released from the hydrates when they are induced with a gas. Carbon dioxide displaces the methane in the clathrate cages. The last method (c) is the thermal stimulation which includes injecting hot water into the well, resulting in the methane hydrate production. In the following sections, four hydrate decomposition techniques for natural gas generation are briefly reviewed.

2.3.1. Depressurising

Different mechanisms have been established to provide commercial gas generation from the gas hydrate reservoirs. The only technique that has been successfully used to economically produce gas from the gas hydrates is the depressurisation method. Depressurisation is a gas generation method that decomposes methane hydrate by declining pressure in the wellbore drilled through hydrate-bearing sediments. Past studies indicated that the depressurisation method (where the pressure of the system is decreased below the decomposition pressure at the prevailing temperature) is one of the most promising techniques for hydrate dissociation. Through reducing pressure, methane hydrate becomes thermodynamically unstable and decomposes due to the geothermal heat flow and sensible heat of the sediments. Therefore, depressurisation is likely the first-generation method performed outside the laboratory. The best operating conditions for this method are high temperature, high permeability, and high geothermal heat flux (Konno et al., 2010, Konno et al., 2014). Verigin et al. (1980) offered an isothermal depressurisation model for a one-dimensional linear system of gas hydrates in a semi-infinite stratum, where the heat was considered to flow immediately from the environment to the hydrate bulk. Holder and Angert (1982) developed a methane hydrate general depressurisation model in which the heat of decomposition is achieved from the sensible heat of the reservoir itself. They showed that the hydrate gas can be produced around 20–30% of the total gas production. Burshears et al. (1986) modified the previous model (Holder and Angert, 1982) to be used for other kinds of gas hydrates. Yousif et al., 1991a, Yousif et al., 1991b studied a 1-D numerical model to mathematically analyze the decomposition in a sandstone system using the depressurisation method by applying the mass and momentum balance conservation laws for each phase. The numerical and experimental results revealed that the methane gas is produced along with an appreciable amount of water in the hydrate decomposition process within the porous model. Sun and Chen (2006) used an experimental methodology to investigate the impacts of gas composition, porous medium, and additive to obtain adequate knowledge/understanding of the depressurising dissociation operation. Goel et al. (2001) modified a model to estimate the efficiency of the hydrate decomposition in a porous medium by using radial diffusivity equation where the gas mass balance in a gas hydrate well was analytically solved. Based on the depressurisation method, Sung et al. (2000) utilized a numerical mathematical technique to obtain a 3-D multiphase (e.g., water, gas, and hydrate) system where an implicit pressure-explicit saturation technique was employed. Results of their study demonstrated the effects of the momentum and mass transfer mechanism while increasing permeability. Ji et al. (2001)presented a parametric sensitivity analysis about the methane production by decreasing well's pressure in the reservoir. The results illustrated that the gas generation rate is dependent on the temperature and pressure of the reservoir, and zone permeability (Ji et al., 2001). The depressurising method was also studied by Kono et al. (2002) to examine the decomposition rate of CH4 hydrate which was adjusted by controlling the porous sediment parameters. Sun et al. (2005) also investigated the gas generation from sediments including methane hydrate by depressurisation. They noticed that the laboratory-scale tests were often decomposition controlled, but the field-scale processes were mainly affected by the flow rate and flow regime. They also showed that the rate of gas generation is more susceptible to the surrounding heat transfer coefficient than the longitudinal conduction coefficient. Ruan et al. (2012) provided a numerical simulation for gas generation in gas hydrate reservoirs by depressurisation in the longitudinal and radial directions, they concluded that the gas generation in the longitudinal direction is slower than that in the radial direction. Also, they investigated the effects of permeability, initial hydrate saturation, intrinsic porosity on the gas generation. Oyama et al. (2009) carried out an experimental and theoretical study and defined a decomposition model as a function of mass transfer and heat transfer rate over the gas generation process. The results showed that the rates of gas generation and decomposition are affected by the production pressure. It was also concluded that one of the most significant factors affecting the dissociation is the heat transfer from the surrounding (Oyama et al., 2009). In addition, an economical sensitivity study and a simplified analytical method on modeling of gas generation from hydrate by depressurisation have been implemented by Khataniar et al. (2002). Increasing the recovery factor is an important goal that needs to be clarified through systematic experimental and theoretical investigations (Konno et al., 2016). Konno et al. showed in their latest work that the cyclic depressurisation is a stable heat source methodology driven by the geothermal heat flow. The technique is economically and environmentally sound (Konno et al., 2016). A part of related research studies on the depressurisation operation are summarized in Table 4 for further information.

Table 4. Summary of experimental studies on gas hydrate dissociation by depressurising.

Researcher	System	Purpose	Pressure (atm)	Temperature (K)
Verigin et al., 1980	Natural Gas Hydrate	Introduced an isothermal depressurisation model in a semi-infinite stratum.	Less than 100	263
Holder and Angert, 1982	Methane Hydrate	Presented a methane-hydrate global depressurisation model.	More than 30	295
Burshears et al., 1986	Ar, N2, CO2 and H2S Hydrates	Developed Holder model to some another kind of gas hydrates.	40–200	283
Yousif et al., 1991a	Methane Hydrate	Modified a 1D numerical model to simulate mathematically model in porous media sandstone.	20–35	274
Sung et al., 2000	Methane Hydrate	Developed a numerical, 3D and multiphase model by using an implicit pressure explicit saturation technique.	40	280.15
Ji et al., 2001	Methane Hydrate	Conducted a parametric study of methane production by depressurising.	20–160	282
Kono et al., 2002	Methane Hydrate	Investigated the rate of CH4 hydrate dissociation by the control of porous sediments properties.	67–135	273.5
Oyama et al., 2009	Methane Hydrate	Developed a decomposition model through an experimental study on gas production to elucidate the dissociation characteristics.	103	285.45

2.3.2. Thermal stimulation

Thermal stimulation is accomplished by increasing temperature above the hydration temperature at an equilibrium condition. In thermal stimulation, the energy usage in the decomposition and generation should not be greater than the energy that can be recovered from the produced gases to meet the economic criteria. Some experimental works on the decomposition behaviour of hydrates by thermal stimulation have been performed (Lee et al., 2011). For example, Kawamura et al. (2003) provided the hydrate decomposition kinetics by dissociating pellet-shaped samples, that mimic naturally happening hydrates in ocean sediments, with a viscous fluid or/and pure water at different temperatures. A high number of thermal stimulation experiments have been employed by adding heated fluids or steam and thus must make up for the intrinsic losses associated with moving heated fluids through the downhole and overburden to the hydrate residues (Pang et al., 2009). Kamata et al. (2005)studied a dissociation test of methane hydrate sediment by the thermal recovery technology. They showed that pressure and temperature in the sample fluctuate between the stability of methane hydrate and decomposition when the water is at a high temperature (Kamata et al., 2005). Thermal stimulation is used as the supplementary means for decomposing hydrate by depressurisation because of the limitation of thermal conduction in the porous media (Moridis et al., 2009, Su et al., 2011). Su et al. (2011) concluded that the heat may be taken back by the liquids flowing in the well before it reaches the hydrate decomposition front, and then the heat impact is significantly decreased and most heat lost. Hence, the producing plan and synchronic heating are impossible for generating gas from the hydrate residues. Heat is operated along the r-axis direction from the heated well but fluids (e.g., gas and water) flow oppositely when a thermal stimulation is applied for generating gas, synchronously. Liang et al. (Tang et al., 2005) claimed that the gas generation rate boosts up with time until it gains a maximum amount, and afterwards it starts to decline. However, the water generation rate remains approximately constant during the generation process. The hydrate content of the sediment, flow rate, and water injection temperature affect the energy ratio of thermal stimulation generation. Jang and Santamarina (2011) have offered a new simulation method for both depressurisation and thermal stimulation production processes in which the volume expansion is incorporated. Considering the gas diffusion and fluid expansion in a pore network modeling method, they showed that the initial hydrate saturation, sediment pore size distribution, and gas expansion factor can play an important role in gas recovery efficiency. It was also found that the gas expansion is a significant factor affecting the in-situ pore pressure. They showed that the simulated gas recovery efficiency is lower for systems with less gas expansion factors, i.e., systems with higher initial pore pressure. Their work showed that the high-volume expansion and thus high recovery efficiency are found in shallow reservoirs with low initial pressures.

2.3.3. Chemical injection

Depressurisation is the most common gas hydrate production method as it appears to be economical. Unlike the inhibitor injection or thermal stimulation, it does not need supplementary costs. Since it takes more time compared to inhibitor injection and thermal stimulation in decomposition, it has a low generation rate, and, therefore a low productivity. It also has been shown that the dissociation is endothermic in this technique. Therefore, there is a chance of gas hydrate reformation while the dissociation reaction occurs (Ji et al., 2001, Yousif et al., 1990). Thermal excitation is more energy efficient than other three methods because the gas hydrates are more sensitive to heat and respond most readily to heat sources. Furthermore, the injected energy can distribute not only across the gas hydrate layer in reservoir but also it can be spread out in the surrounding zones that may not contain gas hydrates (Kamath and Godbole, 1987). This high amount of energy loss is remarked to be the main weakness of the thermal stimulation technology. The chemical injection method includes injecting inhibitors into the gas hydrates to dissociate hydrates in the reservoir. In general, the common inhibitors are methanol and brine. However, the economic and environmental prospects are their drawbacks to be widely utilized in the real cases (Anderson and Prausnitz, 1986, Sira et al., 1990). A few reports have been produced about the methane hydrate decomposition in porous media where various chemicals are added. Ngema et al. (2016b)provided a series of hydrate decomposition data for refrigerants and different concentrations of CaCl2, also they offered correlations for gas hydrate decomposition data for mentioned systems. Kamath et al. (1991) conducted a number of tests examining depressurisation and injection of hot brine solution. Li et al. (2008a) experimentally studied the methane generation treatment from the gas hydrate in a porous system by injecting hot brine with various temperatures and concentrations. They concluded that the generation yield is changed by both concentration and brine temperature. However, the effect of the concentration of the injected brine solution on production efficiently in the porous rocks with different porosities and permeabilities has not been studied yet.