Review on uncertainties in fatigue loads and fatigue life of ships and offshore structures

1. Introduction

Fatigue damage is one of the most critical failure modes for ships and offshore structures. Design against fatigue damage, inspection, maintenance and repairare performed to avoid catastrophic accidents due to fatigue. Fatigue and crack growth in ships and offshore structures are a highly uncertain and complex phenomenon. The fatigue and crack growth limit states have been a major concern in the design, construction and operation stages. Fatigue and crack growth reliability assessment provide rational consideration of the uncertainties associated with fatigue and can support the establishment of design criteria, acceptance criteria for fabrication, and plans of inspection, maintenance and repair.

An accurate description of fatigue loads is an essential prerequisite for performing fatigue damage and crack growth analyses. A major load is due to wave action, which may excite structural responses at approximately the wave frequency or other frequencies depending on structural characteristics (Guedes Soares, 1990e). The random nature of the wave-induced fatigue loads makes it difficult to be numerically estimated and described. Although Classification Societies recommend calculation procedures for wave-induced fatigue loads, the deviation between actual and estimated ones is noticeable (Nitta et al., 1992; Guedes Soares, 1996). The uncertainties associated with the wave spectral model, transfer function, wave scatter diagram, and ship operational profile, lead to the uncertainty in wave-induced fatigue loads (Guedes Soares and Trovão, 1991). In addition, ships and offshore structures may be subjected to significant fatigue loads from other sources, and the involved uncertainties should also be evaluated.

For ships and offshore structures, there are two categories of approaches for practical fatigue damage and crack growth analyses, one based on the S–N curves and Palmgren-Miner's rule and another based on the crack propagationanalyses (Garbatov et al., 2011). The fatigue process taking place in local areas of structural components is extremely complex and still not fully understood. These approaches cannot explain all fatigue-related phenomena, and some influencing factors are not considered explicitly. As a result, uncertainties exist within the approaches. For example, it is observed that there is considerable uncertainty of fatigue lives from constant amplitude fatigue tests under the same fatigue stress loading. The uncertainty may be caused by the variation of weld-induced defects, residual stress conditions, distortion and material properties among different specimens. The fatigue analysis approaches have different physical backgrounds, ranges of application, levels of complexity and accuracy, where the uncertainties are inevitable and probabilistic approachesare required (Kozin and Bogdanoff, 1981, 1983).

Two basic uncertainties are commonly considered: fundamental or intrinsic uncertainty and epistemic or model uncertainty (Guedes Soares, 1997). The fundamental uncertainty concerns the random nature of some physical phenomena or quantities, which random variables or random processes can represent. The model uncertainty describes the limitations of the mathematical models for physical phenomena. It can be derived from comparisons between model predictions and experimental results or predictions from a more sophisticated model. In addition, the statistical uncertainty, belonging to epistemic uncertainty, results from estimating the parameters of the probabilistic models from limited data samples.

Generally, the uncertainties associated with fatigue damage and crack growth can be represented by a set of random variables, which can also be correlated. Different fatigue analysis approaches involve different groups of random variables, and accurately describing random variables is essential for reliability analyses where uncertainties can be treated explicitly (Pittaluga et al., 1991).

The fatigue reliability assessment can be performed considering the uncertainties associated with fatigue damage and crack growth using well-established methods such as the first- or second-order reliability method (FORM/SORM) and Monte Carlo simulation (MCS) technique. The assessment is based on either the S–N curve approach or the crack propagation approach (Madsen, 1997; Shetty, 1997).

By performing the fatigue reliability assessment, the design criteria can be established for a target reliability level (Wirsching and Chen, 1988; Folsø et al., 2002). The target reliability level typically depends on the consequences of failure and the possibility of inspection and plan for maintenance and repair (Guedes Soares and Garbatov, 1996b; Garbatov and Guedes Soares, 1998). Some target reliability indices or failure probabilities for offshore structures were reviewed by Jiao and Moan (1992) and Ambühl et al. (2015). If there are no specifications in design codes, the target reliability index can also be determined based on the assessment of existing structures (Folsø et al., 2002).

Instead of calculating the reliability index for each design case to meet the target, the design fatigue factors (DFFs) or partial safety factors (PSFs) are practically used in a deterministic structural design against fatigue to ensure that the design can achieve the target reliability level. The requirement of DFF for different offshore industries and conditions are specified in some design codes (ISO19902, 2007; DNVGL-ST-0119, 2018, DNV-OS-J101, 2013). Some DFFs may be established in a period when high uncertainties related to the overall performance exist, which is especially true for some new types of marine structures at a prototype level (Ambühl et al., 2015). The uncertainties may be decreased due to gained knowledge, and the uncertainties description may be updated due to the inclusion of more data. The new DFF can be calibrated for an optimal design with low costs. The DFFs have been calibrated for offshore structures (Zhao, 2021), offshore wind turbines (OWTs) (Márquez-Domínguez and Sørensen, 2012; Velarde et al., 2020), wave energy converters (WECs) (Ambühl et al., 2015). Besides, a reliability-based design can also be performed based on the fatigue reliability assessment (Ramsamooj and Shugar, 2002; Feng et al., 2015).

The fatigue reliability assessment can support the establishment of acceptance criteria for fabrication for a target reliability level (Dong et al., 2019, 2021c). Welding Imperfections are inevitable in ships and offshore structures (Gaspar et al., 2011; Garbatov et al., 2016a). Some imperfections are known to impact fatigue strength, e.g. misalignment, undercut and lack of fusion, and they are subjected to uncertainties (Remes, 2008; Dong et al., 2019; Dong et al., 2021c, b). Some codes can find acceptable criteria for imperfections (VSM, 2003; DNVGL-CG-0129, 2015a). The acceptance criteria can be treated as characteristic values of probability distributions. The acceptance criteria for a target reliability level can be obtained by trial and error and implemented in the fabrication standards.

The fatigue reliability assessment can also support the establishment of inspection planning (Faber, 2005; Garbatov and Guedes Soares, 2011b). The crack propagation analysis based on fracture mechanics is especially relevant for the assessment because it can incorporate crack size information. The formulations of the fatigue reliability assessment involving inspection are similar and have been used in a large number of studies (Moan et al., 1993; Madsen, 1997; Guedes Soares and Garbatov, 1998; Rajasankar et al., 2003; Faber, 2005; Ayala-Uraga and Moan, 2007; Dong et al., 2012; Dong and Frangopol, 2016; Lotsberg et al., 2016; Doshi et al., 2017). The initial inspection may be performed at the time when the predicted reliability index, which varies with time, is crossing the target reliability level. Depending on the result of the inspection, the predicted reliability index is updated, and the next time for inspection can be estimated. Guidelines on inspection planning for fatigue cracks in offshore structures using probabilistic methods have been recommended by DNVGL-RP-C210 (2015b).

The present study focuses on the governing factors involved, i.e. the uncertainties associated with the wave-induced fatigue loads and how they affect the fatigue damage and crack growth of ships and offshore structures, which is quantified in fatigue reliability assessments. The uncertainties related to fatigue loads are introduced in Section 2. The uncertainties involved in the S–N approach and the crack propagation approach are discussed in Section 3 and Section 4, respectively. Conclusions are summarized in Section 5.

2. Fatigue loads

The fatigue loads, as one of the primary factors in any fatigue damage analysis, are generally specified or recommended by design codes, e.g. (DNVGL-RP-C205, 2020). However, the recommended fatigue loads are most likely conservative approximations of actual ones, e.g. the distribution of significant wave heightused in the classification rules may differ significantly from the real values and leads to conservative fatigue life predictions (Li et al., 2014). The fatigue reliability assessment needs an appropriate description of the uncertainty associated with the fatigue loads. Accounting for the uncertainty related to the loads and structural response is essential for the design and operations of marine structures (Papanikolaou et al., 2014).

2.1. Wave-induced fatigue loads

The fatigue damage of ships and offshore structures is mainly caused by wave-induced fatigue loads. Predicting wave-induced loads on marine structures is challenging (Temarel et al., 2016). In most engineering practices, the wave-induced fatigue loads are represented by stress range distributions other than time-domain stress histories. The response for a short-term sea state is assumed to be a narrow-banded Gaussian process, and thus the load ranges follow a Rayleigh distribution. Correction may be performed to account for the wide-banded conditions. The long-term load descriptions are the accumulation of a large number of short-term conditions.

The short-term structural response predictions depend on the wave spectrumand the transfer functions. Guedes Soares (1990b) identified the sources of uncertainty in the spectral description of wave elevation in a stationary short-term sea state. Theoretical models were formulated to quantify the uncertainty of response variance due to the spectrum shape. Later, Guedes Soares (1991)proposed a model that quantifies the model uncertainty of different theories of wave-induced ship motions and loads. Model uncertainty factors were proposed to correct the theoretical predictions for systematic deviations and to quantify their uncertainty. The nonlinearity of the response was also considered and modelled. A formulation was developed to quantify the influence of the transfer function uncertainty on the short-term response variance. Yang et al. (2021) performed model tests of a semi-submersible platform to evaluate the model uncertainty of the transfer functions when using the numerical method. It was shown that the model uncertainty was different for different load components, and the bias was relatively significant for some cases.

The long-term structural response predictions involve more factors that are subjected to uncertainties, e.g. the spectral model adopted, transfer function, heavy weather manoeuvring model, the wave short-crestedness and long-term directionality, and the choice of the wave scatter diagram, among others (Guedes Soares and Trovão, 1991; Guedes Soares, 1999). The uncertainty of the long-term distribution can be characterised by the uncertainty of the response value at 10−8 exceedance probability or the uncertainty of the resultant fatigue damage. The wave-induced fatigue loads depend on locations and become complex in some areas, like welded joints (Garbatov and Guedes Soares, 2011a, 2012) or the side shells of ships (Folsø, 1998). Most studies only analysed the vertical wave-induced bending moment for simplicity.

Guedes Soares and Moan (1991) assessed the model uncertainty of the long-term distribution of the vertical wave-induced bending moments to be used in the fatigue design of ships. The effects of ship type, speed, route and wave climatology on the long-term distributions were investigated. It has been shown that for a large number of ships, the mean bias of the ship rule moment at 10−8 and 10−4 exceedance probability is on the non-conservative side, with a coefficient of variation (COV) of about 13%. The ship speed affects the characteristic values of the long-term distributions significantly. Compared with the North Atlantic and the North Sea routes, the other ship routes may yield response values with a reduction of up to 20%. Different wave climate databases yield up to 25% mean bias in the characteristic value of responses for a group of ships. In addition, Guedes Soares (1999) provided information about the uncertainties only involved in the calculation procedure leading to the long-term distribution of wave-induced bending moments on ships. A 7% and 9% variability for the 10−8 characteristic values was obtained. Garbatov and Guedes Soares (2012) analysed the importance and interaction between various factors related to the fatigue damage assessment of ship structures, including main ship characteristics, wave climatic data, wave spectra, and heading distributions.

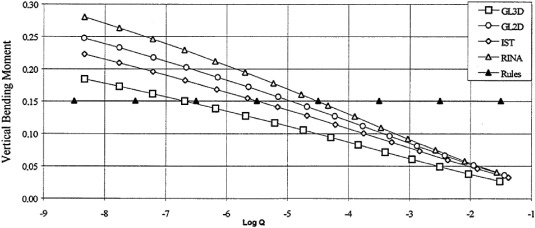
It has been shown by Guedes Soares (1996) that when using the same wave data but adopting transfer functions calculated by different codes, the uncertainty of the vertical bending moment at 10−8 exceedance probability for a containership was 15%, see Fig. 1. A relatively large degree of uncertainty associated with predicted midship wave-induced sectional loads on a container ship using different codes was also demonstrated by Schellin et al. (1996). The uncertainties of the stresses caused by wave-induced bending moments and shear forces were determined. It was concluded that the uncertainties of 9% were obtained for principal stresses while a value of 45% was obtained for shear forces. Comparison with experimental measurements from model tests indicated no clear tendency for more accurate results to be obtained by the two-dimensional strip theories or the three-dimensional panel method. Note that the uncertainty can be reduced if the transfer function calculation codes were based on the same theory (Guedes Soares, 1999). In a recent round-robin study (Rörup et al., 2017), the long-term distributions obtained from 3D Green's function method are close to each other. The limitation of the above analyses regarding the transfer function is the ignorance of the non-linearity of the response, which can be represented by an uncertain modelling factor that is imposed on the linear transfer function (Guedes Soares and Schellin, 1996). Li et al. (2014) compared various typical direct calculation approaches involving different methods for wave load, stress, and fatigue. The predicted fatigue damages using these approaches were compared with those from full-scale measurements. It was concluded that most of the direct calculation approach investigated yield similar fatigue damage estimates. The approach that employs nonlinear time-domain hydrodynamic analysis and the finite element method leads to reasonable and conservative results.

The effect of ship speed and relative heading on the short-term structural response is reflected in transfer functions. In determining the long-term distribution of load effects, the ship speed and heading profiles are essential inputs but generally assumed in a simplified form, e.g. uniform distribution of relative headings and constant design speed. In severe sea states, it is a common practice to change the speed and course of the ship to reduce the wave-induced response. Thompson and Ellis (2020) investigated the influence of ship speed and relative heading distributions on fatigue damage accumulation of two sister naval ships. It has been shown that the operation profiles with and without rough-weather speed and course change lead to significantly different estimated fatigue damages. Yosri et al. (2022) investigated the effect of ship speed on stress transfer functions and fatigue damages. The maximum stress range per unit wave amplitude increases with the ship's forward speed. The damage resulted from the adoption of 2/3 of the ship design speed equals to that resulting from the reduction of ship speed based on the wave heights during the navigation. Applying zero forward speed gives slightly less conservative fatigue damage.

Other recent work, despite not being specifically related to fatigue loads, provides additional insight into these matters by covering uncertainties in long-term wave formulations (Bitner-Gregersen et al., 2022) and wave-induced responses in different conditions (Parunov et al., 2020, 2022; Abdelwahab et al., 2022).

Reliable wave statistics experienced by ships and offshore structures during their service life are essential for fatigue life prediction. Generally, the Classification Societies provide the wave statistics as a joint probability of significant wave height and mean wave period, known as a wave scatter diagram. When using the same transfer function but different wave data sources, i.e. the data of IACS, Hogben and Lumb, Walden, David Taylor, and Global Wave Statistics, an uncertainty of 14% was obtained for the vertical bending moment at 10−8 exceedance probability for a containership (Guedes Soares, 1996). The uncertainty in ship load characteristics and accumulated fatigue damage arising from using the Global Wave Statistics data were assessed for different ocean areas (Bitner-Gregersen et al., 1995). The long-term ship response characteristics varied strongly for different ocean zones. The accumulated fatigue damage within an ocean zone was not uniquely defined by the extreme response within the same zone. The actual wave environment encountered by individual ships may not be consistent with that provided by the classification societies' guidelines because the latter is unlikely to consider operational conditions for individual ships (Mao et al., 2010). It has been shown by Li et al. (2014) that various sources of wave environments and the variation in wave models are important sources of uncertainty in fatigue life prediction. Recent comparisons of current environmental data sources can be found in some studies (Stopa and Cheung, 2014; Campos and Guedes Soares, 2016).

If the wave statistics are from voluntary ships, bad weather avoidance is already inbuilt. While, in cases where the wave statistics are from fixed measurements or hindcasts, modelling the bad weather avoidance is necessary for ships (Guedes Soares, 1996). Guedes Soares (1990a) investigated the effect of heavy weather manoeuvring on the wave-induced vertical bending moments by assuming the non-uniform distribution of headings. It has been shown that although such manoeuvring eases the ship's motions, the wave-induced bending moments may be increased. The effect of heavy weather avoidance on the long-term wave-induced load on ships was also investigated by Shu and Moan (2008). Heavy weather avoidance was modelled by modifying the wave scatter diagram according to the operability criteria. The uncertainty associated with the model was studied by considering three types of modifications. The 10−8 predictions of vertical bending moment amidships can be reduced. The quantitative assessment of the influence of rough weather avoidance on the wave climate ships experience in their routes was presented by Vettor and Guedes Soares (2016). A reduction of the mean significant wave height encountered by ships in their operations was determined quantitatively. In addition to the ship motions, fatigue damage can be an additional criterion for heading selection. Guachamin-Acero and Portilla-Yandún (2021) provided criteria for heading selection to reduce fatigue damage of ships under the action of directional (2D) bimodal (Guedes Soares, 1984) and multimodal wave spectra (Boukhanovsky and Guedes Soares, 2009). The fatigue damage can be reduced by about 50% when the ship heads to the least energetic wave component of 2D wave spectra.

In addition to the wave statistics provided by Classification Societies, some other statistical wave models have been developed to describe more realistic wave environments along arbitrary shipping routes based on different data sources, e.g., hindcast data, satellite measurements, buoys, etc. Baxevani et al. (2009) proposed a spatio-temporal model, which can simulate the variability of significant wave height over large areas by stochastic fields. The storm wave model and its extensions (Tomita et al., 1995, 2004; Kawabe, 2002; Prasetyo, 2013; Li and Cui, 2014; Li and Guedes Soares, 2017; Li et al., 2020) divided the wave conditions into either storms or calm seas. De Gracia et al. (2019)compared the two statistical wave models with wave measurements. The effectiveness of the wave models was demonstrated by comparing the stochastic nature and the statistical characteristics of simulated sea state histories with those of measured data.

Statistical uncertainty of wave conditions for a relatively short period in a fixed location is significant. Scatter diagrams of a fixed location for 1-, 2- and 4-year periods, as well as 29 years, were applied by Moan et al. (2005) to determine the typical wave-induced response of an FPSO and a semisubmersible. Compared with the 29-year distribution, the variation in the annual distributions is considerable. Li et al. (2020) performed 1-year crack propagation simulations based on the hindcast data, and the crack propagation results were significantly different when using hindcast data from different years.

The uncertainty in the total number of response cycles for ships and offshore structures is also interesting for fatigue analyses. The total number of cycles depends on the sea state's average period and the ship's operational schedule (Guedes Soares and Moan, 1991). The former will vary with the ocean areas along the different ship routes, while the latter depends on the operational profile of each ship type. Guedes Soares and Moan (1991) collected results for different types of ships and ocean areas and found that the total number of responses varies in a range between 5 × 107 and 9 × 107.

The above studies on wave-induced fatigue loads mainly focus on hull girder loads in wave frequency. Some additional fatigue loads may also be subjected to significant uncertainties, which are not covered in detail in this review, e.g. the springing and whipping that may contribute significantly to the total fatigue loads, the fatigue loads on the side structural details near and below the splash zone caused by intermittent wet and dry surfaces.

Some papers that deal with the combined effect of wave frequency response and vibratory response, although not specifically assessing its effect on fatigue are Corak et al. (2015a), Corak et al. (2015b), Corak et al. (2018), Kim et al. (2015), Shi et al. (2016), Takami et al. (2018), Lakshmynarayanana and Temarel (2020), Jiao et al. (2021a) and Jiao et al. (2021b). The uncertainty formulations associated with this type of wave-induced response are studied by Terziev et al. (2020), Wang et al. (2021) and Huang et al. (2022). Being able to reproduce the vibratory response of the ship hulls, the effect on fatigue can be determined by comparing the number of cycles of the combined response to the ones when simulating only the wave frequency response.

The specific influence of this type of response on fatigue has been addressed by Drummen et al. (2008), Hu et al. (2012), Han et al. (2017) and Yang et al. (2020). Since many studies have indicated the great contribution of vibratory response on the total fatigue damage, the uncertainties associated with the models for the response prediction and the relavent safety factors should be further investigated.

2.2. Fatigue loads on offshore wind turbine

In addition to the wave-induced fatigue loads, some other sources of fatigue loads also exist, requiring additional considerations in fatigue analyses of the ships and offshore structures. Offshore infrastructure has extended its application from the oil and gas industry to the offshore wind industry. For OWTs, the dynamic response is more significant than traditional platforms due to the wind load effect. The contribution to fatigue damage of welded multi-planar tubular joints from wind loads can exceed 60%, and the number of stress cycles due to wind and wave loads in a year can exceed 7 × 107 cycles (Dong et al., 2012).

Dong et al. (2011) analysed the dynamic response of jacket-type OWT due to wind and wave loads using a decoupled procedure. It has been shown that the long-term distribution of hot-spot stress ranges of multi-planar tubular joints can be represented by the Weibull distribution and the generalized gamma distribution. The main uncertainties associated with the procedure of fatigue loads determination were identified and analysed by Dong et al. (2012), including the uncertainty in long-term distribution prediction of environmental conditions, in the simulation of the stochastic wind and wave processes, in aerodynamic loads and hydrodynamic loads calculation, in global dynamic response analysis of jacket wind turbine. The effects of different uncertainty levels on the fatigue reliability index were significant, and the COV should be continuously refined.

The coupled hydro-aero-elastic response and fatigue loads of a bottom-supported OWT under different wind conditions were analysed by Marino et al. (2017) for different wave modelling assumptions. Nonlinear modelling of hydrodynamic forcing can lead to resonant vibrations of the tower and consequently significant stress cycles, implying that the model uncertainty should be considered when using linear wave models.

The sensitivity of fatigue loads concerning primary structural, geotechnical and metocean parameters was investigated for a 5 MW OWT with a gravity-based foundation (Velarde et al., 2019). The complex interactions between the OWT structure and the environment are shown in Fig. 2. Results show that parameter significance rankings vary with the design load case. The fatigue loads' uncertainty was highly influenced by turbulence intensity and wave load uncertainties, while uncertainties in soil property suggested significant nonlinear or interactive effects.

Yeter et al. (2015a) performed a fatigue damage assessment of a fixed OWT tripod support structure due to combined wave and wind-induced loading as a basis for the fatigue reliability assessment. Even though the time-domain simulation of complete turbine dynamics has become a common practice, an approach based on the dynamic response analysis in the frequency domain was used due to its efficiency. Yeter et al. (2019) analysed the uncertainty in estimating a monopile foundation's natural frequency due to the uncertainties in modelling methods employed for the soil-pile interaction and the soil characteristics. The natural frequency would significantly affect the fatigue life of the monopile support structure.

The beneficial effect of wave directionality on fatigue damage for a vertical circular cylinder was assessed by Vugts (2005). The fatigue damage sensitivity to wave directionality on large-diameter monopile foundations of OWTs was investigated by Horn et al. (2018b) based on a frequency-domain approach. It was concluded that the effects of wave spreading and swell separation on the long-term fatigue damage were noticeable. Joint distribution of all relevant environmental parameters, including continuous directional description, was proposed by Horn et al. (2018a), which is suitable for the long-term probabilistic design of OWTs. The impact of environmental load uncertainties on the spatial fatigue reliability of OWT foundations was investigated by Horn et al. (2019). The fatigue reliability for a detailed wind directional model, wind-wave misalignment, and a second-order wave load model was assessed and compared with that from a base case. Hegseth et al. (2021) evaluated the impact of the description of the wind and wave loads on the fatigue reliability and optimal design of a 10 MW spar OWT. They found that the turbulence modelling and misalignment greatly impacted the fatigue loads.

Stochastic representations of turbulent wind and irregular waves are used in time-domain simulations of OWTs. The variability due to finite sampling of this input loading is an important source of simulation error, which can be reduced by either increasing the number of short-term simulations or increasing the simulation length (Zwick and Muskulus, 2015).

Marine operations, e.g. the installation of OWTs, need to be planned and implemented considering environmental conditions and operation limits for motions and loads of marine structures. The uncertainty inherent in weather forecasts, notably that in the significant wave height, was studied by Natskår et al. (2015), and a method to assess the reliability of weather forecasts was described. The operation limits are normally given in terms of sea state parameters. A general methodology for assessing operation limits, including the uncertainties in wave spectral shape, was proposed by Guachamin-Acero and Li (2018).

2.3. Low cycle fatigue loads

For most ships and FPSOs, the fluctuation of the still-water loads may lead to a limited number of significant load cycles, usually referred to as low cycle fatigue (LCF) loads (DNVGL-CG-0129, 2015a), see Fig. 3. The still-water loads result from the action of the self-weight of the ship, deadweight and buoyancy. The fluctuation of the still-water load is mainly due to the changes in loading conditions, e.g. loading or unloading of cargos. The significant load cycles may be the most damaging event for structures.

Dong et al. (2021a, 2021c) modelled the LCF loads considering the uncertainty in the static and dynamic load effects. The treatment was extended from that of Classification Society rules, where the LCF loads are modelled as deterministic constant amplitude loading. From the analysis of operational records from many ships, it was concluded that the long-term variability of still water load effects can be described statistically (Guedes Soares and Moan, 1988), which implies that the extremes can be derived from stochastic models (Guedes Soares, 1990d). However, the extremes that are observed in operation can be subjected to additional uncertainty resulting from human actions (Guedes Soares and Moan, 1988; Guedes Soares, 1990c). The variation in static load effects is controlled by the amount of cargo and its distribution along with the ship. The cargo's amount and distribution depend on its transportation availability and the master's decision. Because the two factors are uncertain, probabilistic models of static stress should be constructed.

A normally distributed random variable can generally describe the static load effect, and the distribution depends on the loading condition (Guedes Soares and Moan, 1988). During the voyages, gradual fuel consumption will change the static stress. The variation is significant for some types of ships (Guedes Soares and Dogliani, 2000), while this is not so clear for others (Guedes Soares and Dias, 1996). In addition to the fluctuation of static load effects, the LCF loads involve two extreme wave-induced stress amplitudes during the two loading conditions. The extreme values are also considered as random variables by Dong et al. (2021c), and in general, load combination rules (Guedes Soares, 1992; Teixeira et al., 2013) can be used.

Note that some other sources of significant load cycles lead to LCF. Yeter et al. (2015b) analysed wind turbine monopile supporting structures subjected to LCFdue to abnormal wave loads. The accidental loads due to collision and grounding of ships (Liu et al., 2021) can lead to some extremely large load cycles. Li et al. (2021) conducted a combined experimental and numerical investigation on the unstiffened, single-stiffened and double-stiffened plates subjected to internal blast loading, which can also contribute to LCF.

3. Fatigue analyses based on S–N curve approaches

3.1. Uncertainties in load effects

Uncertainties are associated with almost every step of determining fatigue loads and load effects, complicating fatigue reliability assessments. For example, to investigate the uncertainties of wave-induced fatigue loads on a semi-submersible platform, Yang et al. (2021) introduced the assessment methods and formulas for the quantification of the uncertainty of the wave spectrum, sea wave height, wave loading transfer function, zero-crossing period, possibility of sea state occurrence and wave direction.

Many studies simplify the fatigue loads uncertainty evaluation by imposing a global uncertainty factor. The statistical descriptors of the global uncertainty factor are usually an assumption or from experience. Wirsching et al. (1984; 1988) used a random variable B to describe stress modelling error, which consists of five components: fabrication and assembly operations, sea state description, wave load predictions, nominal member loads, and estimation of hot spot stress concentration factors (SCFs). The statistical descriptors for each component were recommended according to the experience in the design process, and the difficulties in quantifying the modelling error were discussed by Wirsching (1984). Quantification of the stress modelling error was summarized by Wirsching and Chen (1988). It was found that there is a slight conservative bias to stress analyses, and the uncertainties may range from 20 to 50%. Different suggestions on the statistical descriptors were summarized by Folsø et al. (2002), and the modelling error in rule-based load calculation was evaluated by comparing it with the directly calculated loads based on the linear strip theory. Note that these relatively old statistical descriptors may be not appropriate to be imposed on the estimations based on recently developed models because the load and stress analyses models have been significantly improved, leading to a reduction of the error and uncertainty. In a reference (Bai and Jin, 2015), the modelling error in stress prediction was divided into four levels: COV ranges from 15% to 30%, depending on the load and stress analysis methods.

Márquez-Domínguez and Sørensen (2012) also included the stress modelling error in the fatigue reliability assessment. The uncertainty in stress analyses can be decomposed into two parts: the uncertainty related to the determination of loads and the uncertainty related to the determination of stresses given fatigue loads. For wave energy converters, Ambühl et al. (2015) further decomposed the former uncertainty into two parts: the model uncertainty related to wave load calculation and the uncertainty of wave climate. Experimental and numerical wave load results were compared to determine the model uncertainty of wave load calculation. The uncertainty of wave climate depends on the period of available wave data and whether the direction of incoming waves is considered in load calculations. Sørensen (2015) introduced a three-band category for modelling the uncertainty of wind load depending on the accuracy and the assessment method selected for the wind measurement or analysis. Velarde et al. (2020) included a random variable representing the model uncertainty related to modelling of the dynamic response of large monopiles for OWT.

The fatigue loads cannot be directly used in the fatigue analyses, and the S–N curve approach for fatigue analyses relies on stress or strain acting on local areas. In practice, nominal stress, hot spot stress and effective notch stress are used for ships and offshore structures (DNVGL-CG-0129, 2015a; Hobbacher, 2015; DNVGL-RP-C203, 2016). Therefore, the uncertainties involved in determining fatigue stresses from the fatigue loads should be accounted for.

Calculating hot spot stresses of complex structural components may introduce some uncertainties. For offshore tubular joints, parametric formulas may be used to calculate the hot spot SCFs, e.g. the Efthymiou SCF equations (Efthymiou, 1988). Although these equations provide a simple and efficient way to consider the effect of multi-planner braces, their limitations can introduce model uncertainties (Sigurdsson and Cramer, 1996). The uncertainties associated with the modelling of the SCFs were defined at two levels (Sigurdsson and Cramer, 1996). One single common uncertainty factor is assigned to all of the SCFs, which accounts for fabrication inaccuracies and approximations made in the stress calculation or joint classification. Individual uncertainty factors are assigned to the SCFs for each degree of freedom.

In addition to SCF formulas, the hot spot stress can be directly calculated using the finite element method (FEM). Fricke et al. (2008) performed a round-robin study on the numerical analysis of local stresses in ship structural details, which quantified the uncertainties related to the modelling and stress evaluation. The sources of the scatter are mainly due to the different types and properties of the finite element and the mesh density. A typical COV to be expected from the local stress analyses is 5%, while higher scatter may occur in complex details.

There are also uncertainties arising from the imperfection and geometry of welded joints, and the uncertainties in imperfections increase the uncertainty of stress responses. Chakarov et al. (2008) analysed longitudinally stiffened welded decks of a container ship based on FEM. They evaluated the hot spot stress distribution and SCFs resulting from different imperfections, including thickness change misalignment, angular imperfection and rotation of the transverse weld. Dong et al. (2019) included the uncertainty of the misalignment of butt-welded joints in the fatigue reliability assessment. Updated stress magnification factor formula considering the effect of initial deformation of thin plate welded joints were established and used in fatigue reliability analyses (Qiu et al., 2021; Shen et al., 2021). The effect of weld geometric profile on fatigue life of laser-welded HSLA-65 steel was evaluated by Caccese et al. (2006). Different weld toe profiles resulted in significantly different fatigue lives. When a geometry-based SCF was used, the fatigue testdata had much less variability and can be lumped into one master S–N curve.

In DNVGL-RP-C210 (DNVGL-RP-C210, 2015b), a guideline has been provided for the uncertainty modelling of SCF. With lognormal distributions of mean μ = 1, five standard deviation bands are suggested based on the SCF calculation method, see Table 1.

Table 1. Guideline for parameters of SCF uncertainty model (DNVGL-RP-C210, 2015b).

Band	SD(Standard deviation)	Condition
1	0	Use of FEM tools at the considered location for statistically determinate systems with simple fatigue critical details
2	0.05	Use of FEM tools at the considered location for statistically determinate systems with complex fatigue critical details
3	0.10	Use of FEM tools at the considered location for statistically in-determinate systems with complex fatigue critical details
4	0.15	Use of SCF parametric equations for simple fatigue critical details
5	0.20	Use of SCF parametric equations for complex fatigue critical details

3.2. Uncertainties in fatigue strength

According to the Miner-Palmgren rule, fatigue failure occurs when the cumulative fatigue damage D is larger than the fatigue damage at failure Δ, which is usually defined as unity, see Eq. (1).(1) $D = \sum_{i = 1}^{n} \frac{1}{N (S_{i})} \leq Δ$ where D is cumulative fatigue damage, n is the number of stress cycles, Si is the stress range for ith cycle, N(Si) is the number of cycles corresponding to fatigue failure at Si, Δ is the fatigue damage at failure.

Many factors, such as temperature, chemical environments, mean stress, loading sequence, and surface condition, affect fatigue (Wirsching, 1980). The simple law cannot provide an accurate description of a complex phenomenon. To quantify the model uncertainty associated with the rule, fatigue test data from many studies were analysed by Wirsching (1980). It has been demonstrated that the critical value of the cumulative fatigue damage at failure Δ was not always close to 1 but is treated as a random variable whose median values are close to 1, and the COV is relatively large. Wirsching and Chen (1988)found that tests suggested a slight non-conservative bias on welded details, and uncertainties of 30–60% seem to be typical. The lognormal distribution with median 1 and COV = 0.3 was used in many fatigue reliability studies (Wirsching et al., 1990; Dong et al., 2019, 2021b) and recommended by DNVGL-RP-C203 (DNVGL-RP-C203, 2016) for welded joints. A summary of the statistical descriptor from different tests can be found in some studies, e.g. Wirsching (1998). Zhao (2021) found that the COV varies from case to case, and recommended a lognormal distribution with a mean of 1 and COV = 45% based on averaging results from many tests.

One of the well-known fatigue phenomena is the considerable scatter of fatigue strength for similar fatigue tests. The scatter is caused by uncertainties in weld geometry, weld defects, welding-induced residual stresses etc. (Fricke and Müller-Schmerl, 1998). As a result, the constant amplitude loading fatigue test data are located in a scatter band in the log-log plot. For S–N curves represented by NSm=K, it is normally assumed that the slope parameter m is deterministic, and the intercept parameter K is a lognormally distributed random variable. The uncertainty of K thus describes the uncertainty of fatigue lives. The curve representing a survival probability of 97.7%, i.e. the mean-minus-2-standard-deviation curve, is normally used as the design S–N curve in deterministic fatigue analyses. Some more sophisticated statistical models also exist (de Oliveira Correia, 2015).

The uncertainty of fatigue strength, i.e. the intercept parameter K, is important for fatigue reliability analyses (Zhao, 2021). It was shown by Wirsching and Chen (1988) that the COV of K is relatively large and may range from 40 to 70% for different classes of S–N curves, supporting the claim that reliability methods are particularly relevant for fatigue. In fatigue design codes where the hot spot stress approach is used (DNVGL-CG-0129, 2015a; 2016), the standard deviation of logK is assumed to be 0.2 for almost all the S–N curves. The S–N curve for the effective notch stress approach has a standard deviation of logK of 0.206 (Fricke, 2012). Zhao (2021) investigated probabilistic models of the uncertainty of the fatigue strength in the S–N curves frequently used in offshore oil and gas, and the offshore wind industry based on a comprehensive fatigue test database. Fig. 4 compares the uncertainty models recommended in design codes and those proposed based on test results.

In fatigue design codes, the S–N curves consist of two segments. The above-mentioned studies focus on the upper segment. The lower segment tends to be flat due to the existence of a fatigue limit under constant amplitude loading. Therefore, the uncertainty of fatigue strength in the lower segment is larger than in the upper segment. In fatigue design codes, the lower segment has a slope parameter equal to 2m-1, where m is the slope parameter of the upper segment, to consider the variable amplitude loading effects, i.e. the fatigue process is still taking place if the fatigue stresses are lower than the fatigue limit. The uncertainty of fatigue strength for the lower segment is represented by the same standard deviation of 0.2 as the upper segment.

When fatigue test data are limited, the estimation of the design S–N curve becomes uncertain. A study has been carried out to establish which confidence level in the estimation of the design S–N curve from limited data was required to maintain the safety level equal to the safety level which was achieved under an assumption of perfect knowledge (infinitely many fatigue tests) (Ronold and Lotsberg, 2012).

Note that the scatter of fatigue strength can be reduced when adopting a more advanced S–N curve approach because some factors influencing the fatigue strength of welded joints are explicitly considered in the refined approaches. In other words, the width of the scatter band would be decreased due to using a more advanced approach with fatigue stress or strain that includes more factors explicitly. With the development of the S–N curve approach, some uncertainties associated with fatigue strength are transferred to the uncertainties in the fatigue stress or strain. However, the uncertainty quantification of these factors complicates the fatigue reliability assessment. An example was given by Dong et al. (2021c), where a large number of random variables were involved, including those representing the uncertainty of weld geometric parameters, weld defects, residual stresses, material properties etc. However, the trend of decreasing fatigue strength uncertainty is not reflected between the nominal, hot spot, and effective notch stress approaches since their S–N curves have a similar standard deviation of logK.

3.3. Other uncertainties

Besides the uncertainties involved in load effects and fatigue strength, considerable uncertainties exist in the rule-based fatigue strength assessment of ship structures. A benchmark study on fatigue strength assessment procedures used by the classification societies has been performed by Fricke et al. (2002). Although the loading is quite well defined in the upper part of the hull girder, the predicted lives of a padded detail on the coaming vary considerably, between 1.8 and 20.7 years. It has been shown that the high scatter is attributable to different assumptions regarding load effects, local stress analyses, and S–N curves.

Different S–N curve approaches can also yield different fatigue strength assessment results. Different structural stress approaches were discussed and compared with each other by Fricke and Kahl (2005). The application to three welded ship structural components illustrated variations and differences in the analysed stresses and predicted fatigue lives. A fatigue strength assessment was carried out for a side shell connection of a container vessel using both the hot spot stress and the Battelle structural stress approaches (Kim et al., 2009). Fatigue strength predicted by the two approaches at hot spot locations was compared and discussed.

Yeter et al. (2016) performed a fatigue damage assessment comparison of several fatigue damage models, including those of Rayleigh, Wirsching and Light (1980), Tunna (1986), an approach presented by Benasciutti (2004), Benasciutti and Tovo (2006), Zhao and Baker (1992), Rice (1954) and Dirlik (1985) employing the Akaike's information criterion (Akaike, 1974). In this analysis, the fatigue damage model of Dirlik demonstrated a better prediction of the existing data. It was also concluded that among the wide band models, the Tunna method appears to be the best possible solution to estimate the fatigue damage as it overestimates the ‘‘true” rainflow cycle counting fatigue damage by 34% and when the narrow band solution (Rayleigh distribution) is compared to the rainflow cycle counting approach the difference is about 240%.

In some cases, the stress responses of the ships and offshore structures violate the narrow-banded Gaussian process assumption and are described by wide-band spectra with multiple peaks in the frequency domain. The classical frequency-domain approach relying on narrow-banded assumptions becomes inaccurate and conservative. The time-domain approach or updated frequency-domain approach may be used in these cases. The former is considered to be more accurate but less efficient than the latter. Many frequency-domain approaches that can deal with wide-banded processes, wide-banded bimodal processes and non-Gaussian processes were developed (Park et al., 2014; Gao and Zheng, 2019; Gao et al., 2021). Because these approaches have different levels of sophistication, the model uncertainties should be quantified, which can be used in reliability analyses.

The mean stress correction is recommended by fatigue design codes and depends on the still-water load and the welding-induced residual stress. The uncertainties associated with the former were introduced in Section 2.3, and the uncertainty of the welding-induced residual stress was recently investigated by Manai et al. (2020). The considerable uncertainties in the residual stress distribution and possible residual stress relaxation and re-distribution (Hensel et al., 2018) make it difficult to determine a convincing mean stress correction factor.

The effect of corrosion combined with fatigue on ship reliability has been determined by Guedes Soares and Garbatov (1998) and Zayed et al. (2013), among others. The effect of environmental factors on steel plate corrosion under marine immersion conditions has been discussed by Guedes Soares et al. (2011) and in references therein. A detailed study of the effect of corrosion on degrading material properties in small specimens with different levels of corrosion has been studied experimentally by Garbatov et al. (2014b), Garbatov et al. (2016b) and Garbatov et al. (2019), and the effect of fatigue life has also been determined (Garbatov et al., 2014a). The effect of corrosion on fatigue of complete structures has been addressed by Nguyen et al. (2013) and Parunov et al. (2013), among others. The fatigue damage prediction involves corrosion S–N curves after the failure of the corrosion protection system. When the corrosion S–N curve should be used is subjected to uncertainties, and changing the time can significantly affect the fatigue life (Nguyen et al., 2013).

The pit corrosion induced stress concentration was investigated by Shojai et al. (2022a). Three different models for evaluating the stress concetrations were developed: single-pit model, double-pit model and random fields model, among which the double-pit model shows a good agreement with the results of real corrosion surface. The double-pit model can be used in probabilistic analysis of stress concentrations, enabling risk and reliability-based fatigue analysis. The influence of pitting corrosion and the corresponding stress concentration on the fatigue life endurance of structural steel, used for offshore wind support structures, was investigated by Shojai et al. (2022b) based on 3D surface scans. Relatively high SCFs were determined by numerical analyses, and in most cases the hotspots from the numerical model coincide with the crack location detected with Digital Image Correlation. The evaluation of the remaining service life of corroded structures may be achieved based on local approaches for fatigue strength assessment.

4. Fatigue analyses based on crack propagation approaches

The S–N curve approaches are practically used for fatigue design, while they cannot incorporate the crack size information from inspection. In contrast, the crack propagation approaches can describe the gradual development of cracks and hence account for the effect of inspection and possible repair at the different stages of crack growth. The introduction and development of fracture mechanics allow detailed modelling of the fatigue process. Due to the uncertainties involved in the crack propagation analyses and those in the inspection procedure, reliability methods can be used to support the management of inspection, maintenance and repair (Moan, 2005). Some major uncertainties are introduced as follows.

4.1. Uncertainties in initial crack size

Although the fatigue life of structural components generally consists of initiation and propagation phases (Dong et al., 2018a, b; Zerbst and Hensel, 2020), the development of a probabilistic model for fatigue strength that includes both phases is complicated (Scott Martin and Wirsching, 1991). Guedes Soares and Garbatov (1996a) reviewed the time to crack initiation uncertainty models. The Weibull or lognormal distribution was used in many studies. The time to crack initiation was assumed to be proportional to the crack propagation time.

In most studies, the fatigue crack initiation life for welded joints was assumed to be negligible based on the argument of the existence of weld detects (Maddox, 1991). The initial crack size and shape are required in the crack propagation analyses of welded joints. Some studies used the weld defect size distribution (Engesvik and Moan, 1983). In an experimental study (Otegui et al., 1989), the crack initiation sites were observed to be undercuts, slag inclusions, and surface spatters at the weld toe surface. Alam et al. (2010) showed that the crack initiation location can be shifted away from the toe to the weld bead when the toe radius is large, and the surface ripples determine the main stress raiser location for cracking. It can be concluded that the initial crack size is closely related to the size of weld defects located around the weld toe. Summaries of some measured data for weld defects can be found in some studies (Engesvik and Moan, 1983; Thayamballi et al., 1984; Harris, 1995).

For ships and offshore structures, Bokalrud and Karlsen (1982) analysed the data of crack depth referring to undercuts in butt-welded plates, which were represented by an exponential distribution with a mean value of 0.11 mm and an occurrence rate of 16 cracks per m. Moan et al. (2000) analysed the database of cracks detected in tubular joints of jackets located in the North Sea. The initial crack size derived was estimated to have a mean value of 0.19 mm exponentially distributed for an individual crack. In contrast, a mean value of 0.38 mm per hot spot was found. A comprehensive review on this aspect was carried out by Amirafshari et al. (2021). Since most of the weld defect size data were obtained decades ago, some new data of defect rates and defect lengthsrepresenting modern welding technology for ship structures were also provided by Amirafshari et al. (2021). It was found that Hybrid Laser Welding has lower defect rates than other common arc welding processes, and the studied ship data has generally better welding quality compared to published data on offshore structures which could be due to increased welding quality since the 1980s.

Some limitations of the measured defects or cracks should be noticed. The measurements of weld defect sizes are generally time-consuming and laborious. The measured data in the literature may not be suitable for other welded joints because different welding processes can be used. The fatigue cracks may not originate from the measured defects. The number of measured data is limited; thus, the data may not be representative. The measurement results may deviate from the real ones, depending on the method employed.

A common approach to determining the initial crack size is calibrating crack propagation analyses to S–N data (Righiniotis and Chryssanthopoulos, 2003; Ayala-Uraga and Moan, 2007; Lotsberg et al., 2016). The initial crack size distribution is calibrated such that the probability of a fatigue failure at a given number of stress cycles is similar to that from S–N tests. The approach provides sound crack sizes because the stochastic properties of the number of stress cycles obtained in the S–N tests and those calculated by probabilistic crack growth analyses are similar. Righiniotis and Chryssanthopoulos (2003)determined S–N curves of 50 and 97.7% survival probability for four different weld details based on a probabilistic crack propagation model. The distribution of the initial crack depth and the aspect ratio (crack depth divided by crack length) were calibrated, and the two random variables were assumed to be lognormally distributed. Lotsberg et al. (2016) calibrated the initial crack depth in the probabilistic crack propagation model using S–N data. For a T-joint, the calibrated initial crack depth followed an exponential distribution with a mean value of 0.043 mm. Dong et al. (2022) calibrated the initial crack size of single-sided girth welds in offshore pipelines and risers, which is log-normally distributed with a median of 0.35 mm and COV of 0.1.

The calibrated initial crack size is denoted as “fictitious” because it can hardly be documented to correspond to real physical crack sizes (Lotsberg et al., 2016). Some limitations of the crack propagation model contribute to the deviation between the fictitious and real crack sizes. The linear elastic fracture mechanics (LEFM) was used in the calibration, while the small size of cracks may invalidate LEFM. The early fatigue crack propagation may involve the coalescence of different cracks, but the crack propagation model normally considers only one crack for simplicity (Dong et al., 2020).

4.2. Uncertainties in fatigue crack growth rate

Crack growth is a process that contains certain statistical nature. The crack growth test results show that the fatigue crack growth rate (FCGR) varies, even under well-controlled laboratory conditions (Virkler et al., 1979). The scatter in FCGR may be caused by material inhomogeneity.

For welded joints, the variability of FCGR may arise from the variability of material, residual stress, environment, stress ratio and measurements. Fatigue cracks are usually initiated from the heat-affected zone (HAZ) and spend most of their life in that area. Therefore, the FCGR data within the HAZ is more relevant. The scatter may be less than it is when the data from several materials are considered in combination (Engesvik and Moan, 1983). However, it was also observed that the data is only slightly affected by the microstructure within whole material classes such as steels (Kucharczyk et al., 2018). Therefore, the difference in the FCGR caused by different materials may be limited. The material inhomogeneity is significant for HAZ because the microstructure and material properties vary in a very small area. The FCGR data in inhomogeneous material are preferred. The residual stress can change the R-ratio, which is known to affect the FCGR. The presence of a marine environment tends to increase variability (Cheng, 1985).

Some models were proposed to deal with the stochastic fatigue crack growthproblem. To consider the growth process, a random process must be considered (Wu and Ni, 2004). However, the random variable description is simpler and more conservative, and consequently, it is more attractive in practical applications. The probabilistic model for the FCGR is usually discussed in the context of the Paris law:(2) $\frac{d a}{d N} = C {(Δ K)}^{m}$ where a is the crack size, da/dN is the crack propagation rate, ΔK is the stress intensity factor range at the crack tip, and C and m are material constants.

The problem becomes selecting reasonable distributions for the constants (C, m) and estimating the parameters of these distributions. Some studies considered them correlated (Bergner and Zouhar, 2000). The correlation is not linked to a physical property of the material but comes instead from the mathematical expression of the Paris law (Lukić and Cremona, 2001). Some others consider m a deterministic parameter and C a lognormally distributed random variable to absorb all the variability (Thayamballi et al., 1984). Deterministic values of m were assumed, and statistical descriptors of C can be derived from the data provided in BS 7910 (BS 7910, 2013).

The Paris law can only describe the FCGR in the medium range of ΔK. The crack growth threshold or crack growth near the threshold region can be considered by introducing a parameter ΔKth, below which the crack is assumed to be non-propagating or introducing a bi-linear crack growth model (Chryssanthopoulos and Righiniotis, 2006). The consideration is meaningful since most of the fatigue loading effects are low-amplitude stress cycles. The COV of ΔKth is quite high, and the mean value depends on the R-ratio (King et al., 1996). In a corrosive environment, ΔKth tends to zero. The experimental method to determine ΔKth can also introduce some uncertainties (Kucharczyk et al., 2018). The bi-linear formulation of the FCGR was included in BS 7910 (BS 7910, 2013). Both the two segments of the FCGR curve can be represented by Eq. (2), but they have different constants. The effect of the correlation condition of the logC for the two segments was investigated by Ayala-Uraga and Moan (2007).

4.3. Uncertainties in stress intensity factor

The calculation of SIF can be a source of uncertainties. The SIF for a given applied nominal stress S is given as:(3) $K = S Y (a) M_{k} (a) \sqrt{π a}$ where Y(a) is the geometry factor depending on the geometry of the cracked component and the loading condition, e.g. membrane or bending, Mk(a) is the magnification factor that quantifies the changes in the SIF caused by the presence of the surface discontinuity, e.g. the weld toe. The uncertainty of S is reviewed in Section 3.1.

Some general solutions for Y and Mk can be found in BS 7910 (BS 7910, 2013). Note that the Mk solutions are related to the weld geometry, particularly the weld toe radius and flank angle (Dong and Guedes Soares, 2019). The significant effect of the two geometric parameters on the local stress distribution and SIF solutions were investigated using the FEM (Tsang et al., 2018; Mikulski and Lassen, 2019). The uncertainty in the weld geometry, as shown in some studies (Engesvik and Moan, 1983; Pasqualini et al., 2013; Schork et al., 2018), can be the main source of the uncertainty of SIF solutions. The model uncertainty associated with the estimation of SIF depends on the method used. It was suggested to model the uncertainty as a lognormal variable with a mean of unity and COV in the range from 0.07 to 0.2 (Chryssanthopoulos and Righiniotis, 2006). A lower COV may be applied if the SIF is computed using more sophisticated methods, e.g. the FEM.

The effect of welding-induced residual stresses can be considered either in the FCGR data or the fatigue crack driving force parameter. The latter involves the calculation of the residual stress-induced SIF, Kres. The distribution of residual stresses is usually obtained from experimental measurements or numerical simulations on typical weld joints. The uncertainty of the residual stress distribution is relatively large (Wimpory et al., 2003; Hensel et al., 2018; Manai et al., 2020), resulting in the uncertainty of Kres. In some studies, the uncertainty of Kres was attributed to the uncertainty of the material's yield stress, because the residual stress distribution is defined as a conservative empirical formula involving the yield stress (Righiniotis and Chryssanthopoulos, 2003). To consider the uncertainty in the residual stress distribution, Dong et al. (2018c)used a model uncertainty factor to multiply the Kres estimated based on the average residual stress distribution.

4.4. Uncertainties in inspection and repair

The advantage of the probabilistic crack propagation approach is that inspection results may be accounted for to update the estimated failure probabilities (Garbatov and Guedes Soares, 2002; Ayala-Uraga and Moan, 2007):(4) $P_{f, u p} = P [g (t) \leq 0 | I E] = \frac{P [g (t) \leq 0 \cap I E]}{P [I E]} = Φ (- β_{u p})$ where g(t) is the limit state function at time t, βup is the updated reliability index, Φ() is the standard normal distribution function, and IE denotes the inspection event, e.g. no crack detection or crack detection.

Inspections are routinely performed for structures in service and may lead to the detection or no detection of cracks (Guedes Soares and Garbatov, 1996b). The size of a detected crack is measured by a non-destructive inspection (NDI) method. The crack is detected if a(t)>ad, where a(t) is the crack size at time t, which is estimated by probabilistic crack propagation analyses, and ad is the limit size of detection. The NDI detection limit is a statistical quantity rather than a fixed value. It can be given directly from the probability of detection(PoD) curve. The NDI method, the degree of automation, the skill of the operator concerning the test method and the component under consideration, redundancy, the accessibility of the potential defect site, and the material of the component can affect the NDI detection limit and POD curve (Zerbst and Ainsworth, 2003). A comprehensive review of the POD curves can be found in some studies (Georgiou, 2006; Zayed et al., 2007). The POD curves for some frequently used NDI methods for the ship and offshore industry were given by Lotsberg et al. (2016). A model assisted approach for estimation of POD was demonstrated by Rentala et al. (2018), and various issues related to selection of crack sizes distribution, challenges involved in censoring and regression, estimation of distribution parameters were addressed. It was shown by Koh and Meeker (2019) how to fit and compare different models to repeated-measures hit--miss data with multiple inspections with different operators for each crack and how to estimate the mean POD as well as quantiles of the POD distribution for binary (hit-miss) data. A method for estimating POD curves based on Bayesian theorem was presented by Amirafshari and Kolios (2022). If a crack is detected and measured, the measured crack size may be associated with uncertainty. It is generally random due to measurement error or uncertainties in interpreting a measured signal as a crack length. The measurement uncertainty was considered in some studies (Guedes Soares, 1997; Madsen, 1997).

The repair of detected cracks can significantly improve reliability. An initial crack size within the repaired component needs to be considered to estimate this improved reliability. It was stated by Zhao et al. (1994) that the initial crack size of the repaired component is expected to be a little larger than the original initial crack size. However, the original initial crack size was still used for the repaired component. The repair strategy significantly impacts the fatigue reliability of the repaired component (Moan, 2005). It is usually assumed that the repair is made to obtain the initial quality of the weld. Still, if additional improvement measures are introduced, e.g. grinding the shape or toe of the weld, the reliability may be further increased. A database of 204 fatigue-related steel bridge repair cases including failure causes, repair methods, service years, crack occurrence, and welding defect types was reported by Yokoyama and Miki (2017). Eight repair methods were mentioned, including crack removal, reweld, surface treatment, reweld + post-weld surface treatment, bolted splice, shape improvement, stop hole and modification of connection detail. Some repair methods were investigated in detail (Rodriguez-Sanchez et al., 2004; Wu et al., 2010; Barr et al., 2021). The uncertainties associated with those repair methods should be further investigated.

In recent years, the use of composites to repair fatigue cracks has gained attention (Grabovac and Whittaker, 2009). Some studies focus on the ultimate strength of cracked or intact structural components repaired or strengthened by composites (Fu et al., 2016; Shi et al., 2021). Sabelkin et al. (2006) investigated the fatigue crack growth behaviour in a stiffened thin 2024-T3 aluminum panel repaired with a one-sided adhesively bonded composite patch through experiments and analyses. The bonded composite patch repair decreases the stress intensity factor and fatigue crack growth rate significantly. Chen et al. (2014) analysed the effects of fiber reinforced polymer (FRP) materials on crack propagation of non-load carrying cruciform welded joints using both finite element and boundary element methods. The SIFs were reduced, and the improved fatigue lives were determined with fracture mechanics and validated with test results. The fatigue behaviour of aluminium alloy 2024T3 v-notched specimens repaired with a composite patch under block loading was analysed experimentally by Albedah et al. (2016). For decreasing blocks loading, the retardation effect was attenuated by the presence of the patch which lead to lower fatigue life for repaired specimens. Hu et al. (2022) demonstrated the good fatigue behaviour of CFRP strengthened cracked DH36 steel plates from −60 to 20 °C, and proposed a theoretical method for fatigue life predictionconsidering the effects of temperature. Li et al. (2022) conducted a numerical analysis on the external surface cracked steel pipes reinforced with Composite Repair System. It can be seen from the above studies that the use of composite to repair fatigue cracks can reduce the SIFs and change the crack propagation behaviour. The uncertainties associated with the SIFs of repaired fatigue cracks should be quantified.

4.5. Uncertainties in crack propagation models

A common scenario for crack propagation analyses is that there are different modelling options for some procedures of the analyses, leading to different outcomes. Leander and Al-Emrani (2016) evaluate the effect of different modelling options regarding the load sequence, aspect ratio, crack propagation threshold and FCGR model on the fatigue reliability of welded joints in bridges. It was found that for semi-elliptical cracks, the aspect ratio can have a significant influence on the estimated fatigue life, and should be considered adequately; the account of the crack growth threshold can increase the fatigue life, but the influence depends on the geometry of the detail; the option between a linear and a bi-linear FCGR model derived from one source of data has no significant influence on the fatigue life, but changing the statistical descriptors of the linear FCGR model obtained from another source of data can significantly change the fatigue life.

The above study only mentioned some of the procedures and options. The aspect ratio evolution of semi-elliptical cracks in welded joints can be described, based on two-directional analyses (Dong and Guedes Soares, 2019), by forcing functions (Engesvik and Moan, 1983; Moan et al., 1993; Mikulski and Lassen, 2019), or by constant values (Leander and Al-Emrani, 2016). The SIF solutions for a specific problem may be determined by various empirical formulas or by various methods, e.g. weight function method and FEM. Many FCGR models exist, e.g., models that consider the threshold and unstable stages, the models that consider the R-ratio effect, the models based on the crack closure concept etc. Some options are refined from previous ones and thus have a better performance. In some cases, it is difficult to judge which modelling option is more sophisticated and reasonable.

Many crack propagation models employ crack closure, assuming that a contact between the fracture surfaces could occur even during cyclic tensile loading. The crack closure concept is used to understand the effects of R-ratio, load interaction, etc. (Pippan and Hohenwarter, 2017). Despite the large number of studies supporting the importance of crack closure, there are some studies have doubts about this concept, especially in-plane strain conditions (Antunes et al., 2015). Some experimental results do not support the physical crack closure (Croft et al., 2005; Liljedahl et al., 2010).

Unlike the structures with relatively thin plates in some other industries, the ships and offshore structures use relatively thick plates. The surface cracks and through-thickness cracks in thick plates are more relevant in ships and offshore structures, implying that the plane strain state dominates if the crack size is relatively small (Yue et al., 2018). The models and conclusions resulting from thin plate cracked specimens may need further verification. The load sequence effects in fatigue crack growth of thick-walled welded C–Mn steel members were investigated by Maljaars et al. (2015). The crack closure-based model was able to predict some experimental results with reasonable to good accuracy.

Model uncertainty may be quantified by comparing it with experimental results to evaluate and reduce the modelling error. Besides, a calibration of the probabilistic crack propagation model based on the S–N data can be performed, as done by Lotsberg et al. (2016). Consequently, no matter what modelling options are chosen, the probabilistic crack propagation model results are always consistent with the experimental data.

Depending on the description of the fatigue loading, the fatigue crack propagation analyses can be performed in two ways. If the fatigue loading is a time-domain signal, the retardation or acceleration of crack propagation caused by overloads or underloads can be considered. Many models can consider the load sequence effects under variable amplitude loading (Huang et al., 2008; Cui et al., 2014; Sumi, 2014; Maljaars et al., 2015). Different models and different sequences in loading can result in substantial differences in predicted life. Another description of fatigue loading is the probabilistic distribution of load or stress ranges. The crack propagation analyses are performed using effective stress or a weight average crack growth rate, and the load sequence effects are ignored (Zhang et al., 2018; Li et al., 2020). The predicted results are generally conservative because of the ignorance of the load sequence effects among which the retardation effect usually dominates. The uncertainties in the predicted life are significantly reduced.