State Space Estimator for Plunger Lift

1. Introduction

The natural flowing wells are characterized by a high reservoir pressure, in which the fluids contained in their interior reach the surface freely. That is, the flow of fluids - oil, water and gas - from the reservoir to the facilities is due only to the reservoir energy, which usually occurs at the beginning of the well's productive life (Beggs, 2003). After that stage, artificial lift techniques (Brown, 1988) have to be applied to provide the additional energy required to raise reservoir fluids to the surface by using specific equipment to reduce the bottomhole flowing pressure, and consequently, increasing the inflow.

Plunger Lift (PL) is one of that artificial lifting methods for oil and gas wells in which the plunger is a piston that moves freely up and down through the tubing and depends on the wellbore pressure to make oil or gas rise. In cyclic operation of the PL the well alternates between two conditions: flow, wherein the flow control valve is open, and closed, which is the period in which the flow control valve remains closed. During shut-in, the gas flow through the line is interrupted allowing the piston to fall to the bottom. After a predetermined time, the valve opens and the pressure on the surface falls below the wellhead pressure. The differential force through the piston, due to the reduction of pressure in the tubing above the slug and the high pressure of the well below the piston, is responsible for raising the liquid slug and the piston to the surface.

Studies about models of PL system and intelligent methods for PL are discussed in this section. These theoretical elements compose the basis of the State Estimator for Plunger Lift (SEPL). Many researchers works on the development of different models for PL system. Some of their studies were chosen for the development of the state estimator for PL such as (Rosina, 1983) and (Baruzzi and Alhanati, 1995) (Rosina, 1983) presented a dynamic model for conventional PL only for the period from the opening of the production line until the moment when the piston reaches the surface with an experimental program used for the validation of the model. The model of (Rosina, 1983) supports (Baruzzi and Alhanati, 1995) work that described a method for predicting where it is possible to have liquid accumulation only in the tubing during buildup. Based on the premise that gas can accumulate only in the tubing-casing annular space, they have shown that there is a minimal Gas Liquid Ratio (GLR) to achieve that necessary condition for the model to work. In addition, the researchers developed a dynamic model for PL including an afterflow stage. They performed an afterflow time sensitivity analysis providing some recommendations for optimization of the PL system.

About the application of intelligent techniques for artificial lift, the work (Salahshoor et al., 2013) presented a solution for casingheading instability problem for a gas-lift production well, based on integration of an online interpretation dynamic model and a nonlinear model predictive control (NMPC) scheme. The essential dynamics of casingheading instability is recursively captured by adaptive growing and pruning radial basis function (GAP-RBF) neural networks (NNs) in a nonlinear model structure. Extended Kalman Filter (EKF) and Unscented Kalman Filter (UKF) are comparatively investigated to adaptively train modified GAP-RBF NNs. NMPC methodology is developed on the basis of the identified nonlinear NN model for real-time stabilization of casingheading instability in an oil reservoir equipped with a gas-lift production well. For PL operated wells (Kamari et al.), present a predictive model to yield the maximum liquid production rates based on the least-squares supported-vector machine (LSSVM) algorithm, with tubing size and well depth as the affecting parameters. The coupled simulation annealing (CSA) optimization technique is used for the parameters tuning. And finally, the leverage approach is used to detect the outlier data points present in the data set available for the development of the predictive model.

In this paper a State Estimator for Plunger Lift wells based on EKF algorithm is presented. The PL model consists of a set of discrete Differential and Algebraic Equations (DAEs) in state space. The EKF algorithm is applied to the state space model, resulting in a state estimator capable of processing the measurement signal, thus providing estimates of the state variables. In this case, slug velocity and casinghead pressure are the state variables. EKF algorithm was chosen because of its predictive capacity in models that involve measurements of stochastic nature.

The state estimator developed and presented in this article performs the estimation of the state variables velocity of slug and casinghead pressure. Through the estimation of the state variables can be monitored important variables that make up the process of PL but are not directly measured, such as accumulated slug volume during the buildup period, fallback and piston fall velocity. The monitoring of these variables allows to improve the PL operation since it is possible to predict the production of liquid per cycle and maximize the number of cycles per day. The application of the Extended Kalman Filter (EKF) makes it possible to predict those variables through the state estimation. The EKF treats the physical process as stochastic in nature, since it deals with the noises present in the physical model and in the measurements. The estimates provided by the EKF are considered acceptable because they present a small difference between the data provided by the actual plant meaning a guaranteed level of accuracy.

To present the development and the usage of state estimator in this paper the sections are organized as follows: Introduction where a review of the literature on the development of dynamic models is discussed. In section 2 the PL technique is briefly presented and the stages of the (Baruzzi and Alhanati, 1995) model are presented. Differential and Algebraic Equations systems are discussed in Section 3. In Section 4 the State Estimator for PL is presented and discussed. In Section 5, there is a discussion on computational simulation with SEPL in which data from a real well are used. Final remarks are provided in Section 6.

2. Conventional plunger lift system operation for oil wells

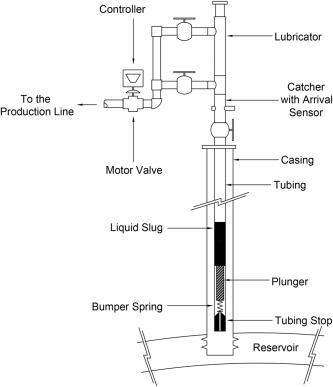
A typical PL oil wells installation shown in Fig. 1 is divided into wellhead and downhole equipment (Brown, 1988, Ras, 2016). The wellhead basically consists of motor valve, lubricator, plunger catcher, arrival sensor, and electronic controller, while downhole elementary equipments are tubing stop, bumper spring and the plunger. The PL operation begins with the piston placed in the bottomhole when the build up period occurs. At that time, the controller sends an operation signal to the motor valve, thereby reducing the pressure in the tubing and consequently creating the differential pressure required to raise liquid and piston to the surface. Produced liquid and gas pass through the production line and the controller sends a closing signal to the flow control valve, causing the piston to fall to the bottom and the cycle then restarts. The complete cycle for a PL installation is divided into three distinct parts: plunger and slug rise, slug production and build up which are explained in section 2.1.

2.1. Plunger lift operation

The stages of the model are described below for the production of oil and gas from the reservoir, being raised through the tubing, and produced in the production line until reaching the separator vessel. As remarked in Section 2, the production cycle of PL well is done in three stages: plunger and slug rise (Stage 1), gas production (Stage 2) and Buildup (Stage 3). The Stage 1 is divided into plunger and slug rise, and slug production.

2.1.1. Stage 1-a: plunger and slug rise

The valve of the production line is opened and the gas contained in the annular space expands into the tubing. Consequently, piston and liquid slug are accelerated upwards, as shown in Fig. 2.

2.1.2. Stage 1-b: slug production

As the slug reaches the wellhead, the liquid begins to flow to the production line. The velocity of the piston and slug increase rapidly in this situation. In this stage, only the dynamics for the slug between the tubing and the production line are analysed. Gas production Stage is divided into two stages: Gas production with liquid at the production line and afterflow.

2.1.3. Stage 2-a: gas production with liquid at the production line

In this stage, the dynamics of the slug is analysed within the production line, from the moment the piston reaches the wellhead until it is fully produced in the separator.

2.1.4. Stage 2-b: afterflow

After the slug is produced and the motor-valve remains open, the afterflow stage begins. In this stage the dynamics of the gas flow towards the separator is analysed. With the flow control valve open, the plunger stays on the surface due to the differential pressure caused by the rising gas flow in the tubing. In this way, the well is producing gas from the tubing to the production line.

2.1.5. Stage 3: buildup

In this stage, the reservoir only supplies fluids to the annular space and tubing since the production line remains closed by the motor valve.

3. Plunger lift model

The dynamic PL model analysed in this work is described by systems of Ordinary Differential Equations (ODEs) coupled with linear and nonlinear constraints. The differential equations were obtained from the conservation balances of conserved extensive quantities, such as mass. Algebraic equations are derived from constitutive relations. Nonlinear algebraic equations of quantities such as heights, velocities, and pressures are the constitutive relations employed in this work. The momentum conservation equation for the model under study is an algebraic equation. Therefore, the model used to describe the physical system, consisting of algebraic and differential equations, is classified as a system of Differential and Algebraic Equations (DAEs).

3.1. Differential and algebraic equations general form

Each stage of the PL Model is described by a system of nonlinear DAEs classified as semi-explicit system (Ascher and Petzold, 1998).(1.1) $\dot{x} (t) = f (x (t), z (t)) .$ (1.2) $g (x (t), z (t)) = 0$

The measurement model is given by(2) $y (t) = h (x (t), z (t))$ where $x \in ℜ^{n_{x}}$ is the vector of differential states, $z \in ℜ^{n_{z}}$ is a vector of algebraic states, $y \in ℜ^{n_{y}}$ is a vector of measured variables, $f : ℜ^{n_{x}} \times ℜ^{n_{z}} \to ℜ^{n_{x}}$ is a mapping of differential equations, $g : ℜ^{n_{x}} \times ℜ^{n_{z}} \to ℜ^{n_{z}}$ is a mapping of algebraic equations, $h : ℜ^{n_{x}} \times ℜ^{n_{z}} \to ℜ^{n_{y}}$ is a state-output mapping.

3.2. Dynamic model

(Baruzzi and Alhanati, 1995) is a dynamic model in concentrated parameters for operation of the PL applied to oil wells which is composed in total of 5 stages, as discussed in Section 2.1. The model of each stage is a DAE system of the form represented by equations (1.1), (1.2).

In this paper, the dynamic models in continuous time will be presented only for Stages 1-a and 1-b because the state estimator for PL presented in this work is limited to the phenomenon of elevation of the slug within the tubing until it is completely produced to the production line.

By sequential replacement of the downstream pressure by the upstream pressure minus the pressure loss from the annular at surface to the separator vessel, the set of equations in $f (x (t), z (t), t)$ and in $g (x (t), z (t), t)$ is reduced to only two, which represent the differential equation balance of mass of gas and the algebraic equation momentum conservation, respectively the first element of the vector $f (x (t), z (t), t)$ and the first element of the vector $g (x (t), z (t), t)$ . These two equations form the vector valued function $ϕ$ (3) of the state vector $χ (t)$ , whose elements are the differential state $v_{s lg} (t)$ and the algebraic state $P_{g c s g T} (t)$ shown in equation (4). For the Stage 1-b it is assumed that the slug velocity in the tubing $v_{s l g t}$ is the differential state slug velocity in (4).(3) $ϕ (χ (t), t) = [\begin{matrix} mass balance \\ momentum balance \end{matrix}] = [\begin{matrix} f_{1} (x (t), z (t), t) \\ g_{1} (x (t), z (t), t) \end{matrix}]$ (4) $χ (t) = [\begin{matrix} slug velocity \\ casing head pressure \end{matrix}] = [\begin{matrix} v_{s lg} (t) \\ P_{g c s g T} (t) \end{matrix}]$ Where $χ \in ℜ^{2}$ and $ϕ : ℜ^{2} \to ℜ^{2}$ .

Stages 1-a and 1-b have the same observed variable, or output variable, the Wellhead pressure (5), and h is the measurement function (6).(5) $y (t) = P_{g t b g T} (t)$ (6) $h (x (t), z (t), t) = [tubing head pressure equation]$

Next, the equations of stages 1-a and 1-b for the PL model are presented.

3.2.1. Stage 1-a: plunger and slug rise

The system of differential equations $\dot{x} (t) = f (x (t), z (t), t)$ for the Stage 1-a is shown in equation (7), in which the vector of differential states $x (t)$ is in the left hand side. The first line of the system is the mass balance for the gas that represents the conservation of mass applied to the gas contained in the control volume consisting of annular, reservoir and gas bubble below the piston. The second line is the instantaneous mass flowrate produced by the reservoir. In the third line, the rate of change of the plunger position is the slug velocity. Fourth line is the slug acceleration equation and the last line of the system is the rate of change of the level of liquid produced by the reservoir that accumulates at the bottom of the tubing.(7) $[\begin{matrix} {\dot{m}}_{g d w n} (t) \\ {\dot{m}}_{g r e s} (t) \\ {\dot{H}}_{p l g} (t) \\ {\dot{v}}_{s l g} (t) \\ {\dot{H}}_{b u p} (t) \end{matrix}] = [\begin{array}{l} {\dot{m}}_{g r e s} (t) - \frac{d}{d t} m_{g c s g} (t) \\ ρ_{g}^{s t d} \cdot G L R \cdot Q_{l r e s} \\ ρ_{g}^{s t d} \cdot G L R \cdot Q_{l r e s} \\ v_{s l g} (t) \\ a_{s l g} (t) \\ \frac{1}{A_{t b g}} \cdot Q_{l r e s} \end{array}]$

The vector of algebraic state variables $z (t)$ is shown below.(8) $z (t) = \begin{matrix} [P_{g t b g T} (t) & P_{s l g T} (t) & P_{g d w n T} (t) & P_{g d w n B} (t) & P_{g c s g B} (t) & \dots \\ P_{g c s g T} (t) & {\bar{v}}_{g u p} (t) & {\bar{v}}_{g d w n} (t) & {\bar{v}}_{g p r o} (t) & m_{g u p} (t) & \dots \\ m_{g c s g} (t) & ρ_{g u p T} (t) & ρ_{g d w n B} (t) & Q_{l r e s} {(t)]}^{T} \end{matrix}$

In this stage, due to the ascending movement of the piston, besides static gas column of the annular space there are also two gas columns in the tubing as can be seen in Fig. 2. The lower column is delimited by the liquid that accumulates at the botton of the tubing and the botton of piston. So the height of the column depends on the height of the piston at time t and the height of the column of liquid accumulating at the base of the tubing from the reservoir. The upper column is delimited by the height of the slug at time t and by the height of the tubing. Both columns have their respective top pressures calculated by the pressure equation of a gas column taking into account gravity and friction. Another similarity between the two columns is their base pressures. Both are calculated by the pressure drop due to the upstream liquid column. For the lower gas column, the pressure in the base is the pressure at the base of the annular space discounted the loss of pressure in the liquid. For the upper column, the pressure at the base is the pressure at the top of the lower column, discounted the pressure losses in the piston and the slug.

The pressure in the separator vessel is a boundary condition and must be equal to the pressure calculated by the equation of a downstream gas line, wherein the upstream pressure is the pressure at the top of the upper gas column.

In the vector $g (x (t), z (t), t)$ shown in (9), the elements from 1 to 6 are equations of downstream pressures, each of them calculated from their respective upstream pressure. The elements 7 and 8 are the velocities of gas in the top of the upper and in the bottom of the lower columns respectively, calculated by the conservation of mass equation. Element 9 is the gas velocity equation in the production line and is related to its upstream velocity by the continuity equation. The equations for the mass of gas contained in the upper column and in the annular space, elements 10 and 11 respectively, are obtained from the equation of state of the real gases. Elements 12 and 13 are the equations of densities for mass conservation in the top of the upper and in the bottom of the lower columns respectively. Element 14 is the reservoir liquid flow equation considering for IPR the Vogel correlation. The friction factors fand the compressibility factors Z presented in the equations of the model, for Stage 1-a and Stage 1-b need to be discussed. For calculating turbulent friction factor, the Colebrook equation (Colebrook and White, 1937) is used that is a function of the absolute rugosity of the pipe and the Reynolds number $(R e)$ . When the flow is laminar, i.e. Reynolds number is less than 2,100, the friction factor is calculated as $64 / R e$ . The method for compressibility factor Z is calculated using the Dranchuck, Purvis and Robinson method (Ikoku, 1984).(9)

The Measurement equation, function $h (x (t), t)$ , as discussed before, is the definition equation for the measured variable $P_{t b g_{T}}$ . For the stage 1-a, it is the pressure above the gas column between the top of the slug and the heading (11).(1

(13) $z (t) = \begin{matrix} [P_{g p r o B} (t) & P_{g t b g T} (t) & P_{g d w n T} (t) & P_{g d w n B} (t) & P_{g c s g B} (t) & \dots \\ P_{g c s g T} (t) & v_{s l g p} (t) & {\bar{v}}_{g d w n} (t) & ρ_{g d w n B} (t) & m_{g c s g} (t) & \dots \\ Q_{l r e s} (t) & L_{s l g t} (t) & L_{s l g p} {(t)]}^{T} \end{matrix}$

In stage 1-b, the slug reaches the surface and is being produced to the production line, so it is necessary to take into account the loss of load caused by the passage of the slug from the tubing to the line. In addition to the gas column of the annular space, there is a single gas column, delimited by the liquid in the bottom and the piston.

In the vector $g (x (t), z (t), t)$ shown in (14), the elements 1 and 2 are equations of pressures in the production line. For the equation of the element 1, the pressure in the gas bubble downstream the slug front is calculated. For the second element, the pressure downstream the slug is the pressure in the top of the tubing minus the pressure losses due to the curves, friction and slug acceleration. Element 3 is the equation for the pressure in the production line at surface. This pressure takes into account the pressure losses due to gravity, slug friction and acceleration of the piston and slug. The elements from 4 to 6 are the same from the vector $g (x (t), z (t), t)$ shown in (9) of Stage 1-a. Element 7 is the slug velocity equation in the production line and is related to its upstream velocity by the continuity equation. Element 8 is the average velocities of gas in lower column calculated by the conservation of mass equation. The average density for mass conservation in the lower column is approximated by the density at bottom as shown in element 9. The equation for mass of gas contained in the annular space, element 10 is obtained from the equation of state of the real gases. Element 11 is the reservoir liquid flow equation considering for IPR the Vogel correlation. Element 12 is the equation for slug length in the tubing, and element 13 is the equation for slug length in the production line.(14) $[\begin{array}{l} P_{s e p} (t) - P_{g p d B} (t) \cdot e^{[- \frac{P M}{R} \cdot \frac{L_{p d} - L_{s l g p}}{{(\bar{Z} \bar{T})}_{s u p}} (\frac{f_{g p d} v_{s l g p} (t) | v_{s l g p} (t) |}{2 D_{p d}})]} \\ P_{g p d B} (t) - P_{t b g T} (t) + \frac{3}{2} ρ_{l} v_{s l g t} (t) | v_{s l g t} (t) | + \\ ρ_{l} \frac{f_{s l g p} L_{s l g p} v_{s l g p} (t) | v_{s l g p} (t) |}{2 \cdot D_{p d}} - ρ_{l} L_{s l g p} a_{s l g p} (t) \\ P_{g t b g T} (t) - P_{g d w n T} (t) + ρ_{l} \frac{f_{s l g} L_{s l g t} v_{s l g t}^{2} (t)}{2 \cdot D_{t b g}} + \\ (\frac{m_{p l g}}{A_{t b g}} + ρ_{l} \cdot L_{s l g t}) \cdot (g + a_{s l g} (t)) \\ P_{g d w n T} (t) - P_{g d w n B} (t) \cdot \\ e^{[- \frac{P M}{R} \cdot \frac{H_{p l g} (t) - H_{b u p} (t)}{{(\bar{Z} \bar{T})}_{d w n}} (g + \frac{f_{g d w n} v_{g d w n B} | v_{g d w n B} |}{2 D_{t b g}})]} \\ P_{g d w n B} (t) - P_{g c s g B} (t) + ρ_{l} \cdot g \cdot H_{b u p} (t) \\ P_{g c s g B} (t) - P_{g c s g T} (t) \cdot e^{(\frac{P M}{R} \cdot \frac{L_{t} b g}{{(\bar{Z} \bar{T})}_{g c s g}})} \\ v_{s l g p} (t) - v_{s l g t} (t) \cdot \frac{A_{t b g}}{A_{p d}} \\ v_{g d w n B} (t) - \frac{d}{d t} m_{g d w n} (t) \cdot \frac{1}{ρ_{g d w n B} (t) \cdot A_{t b g}} \\ ρ_{g d w n B} (t) - \frac{P M}{R} \cdot \frac{P_{g d w n B} (t)}{{(Z T)}_{g d w n B}} \\ m_{g c s g} (t) - {\bar{P}}_{g c s g} (t) \cdot \frac{P M}{R} \cdot \frac{L_{t b g}}{{(\bar{Z} \bar{T})}_{g c s g}} \cdot A_{t c s g} \\ Q_{l r e s} - Q_{m a x} \cdot (1 - \frac{0,2}{P_{R}} P_{g c s g B} (t) - \frac{0,8}{P_{R}^{2}} P_{g c s g B}^{2} (t)) \\ L_{s l g t} - L_{t b g} + H_{p lg} (t) + L_{p lg} \\ L_{s l g p} - (L_{s lg} - L_{s l g t}) \cdot \frac{A_{t b g}}{A_{p d}} \end{array}] = 0$

The gas mass conservation equation in this stage is the same as in stage 1-a. The momentum equation takes into account the presence of liquid in the line, which causes variation in