A new relative permeability model for chemical flooding simulators

1. Introduction and background

Two and three-phase relative permeability measurements at low interfacial tension (IFT) have been published by Delshad et al. (1985), Fulcher et al. 1985,Delshad et al., 1986, Delshad et al. 1987, Skauge et al. 1988, Delshad 1990, Foulser et al. 1992 and Cinar and Orr, 2005. Microemulsion relative permeability models have been proposed by Hirasaki et al. (1983), Camilleri et al. 1987, Delshad et al., 1996, Khan et al., 1996, Bo et al., 2003, Gullapalli and Chih-Hung 2011, Najafabadi et al. 2012, Patacchini et al. 2014, and Shi et al. 2017. Despite all these attempts over the past 34 years, none of these relative permeability models can model the microemulsion phase across different phase behavior environments from oil in water, to middle phase to water in oil microemulsion without discontinuities. For example, the relative permeability at the boundary between a Type I microemulsion and a Type III microemulsion should be the same i.e. continuous. Even this elementary requirement is difficult to achieve using traditional approaches. Other desirable features should include agreement with two and three-phase microemulsion relative permeability and oil recovery data, and relative simplicity for use in reservoir simulators with a minimum number of model parameters that can be estimated from experimental data in a straight forward way. Satisfying these requirements has turned out to be an extremely challenging task.

The objective of this study was to develop a simple two and three-phase microemulsion relative permeability model with relatively few parameters and without non-physical discontinuities that is practical for use in chemical flooding simulators (Lashgari, 2014; Patacchini et al. 2014; Lashgari et al. 2015; Tagavifar et al. 2016; Han et al. 2017). Discontinuities in relative permeability cause numerical problems such as oscillations that can cause severe reductions in the size of the time steps. Non-physical discontinuities also cause errors in the model predictions of important phenomena such as phase trapping and surfactant retention. Thus, there was a need to develop a new model without non-physical discontinuities. The need for a model that was continuous above the CMC has been known for a long time (Khan et al., 1996; Gullapalli and Chih-Hung, 2011), but it was a very challenging task to develop such a model because of the complexity of three-phase microemulsion phase behavior.

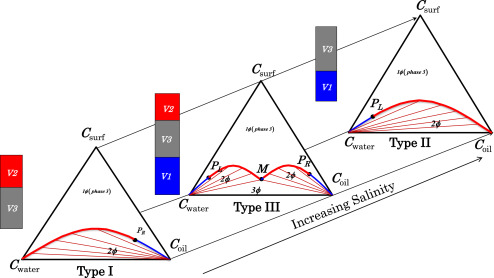
The change in microemulsion phase behavior types as a function of salinity is depicted in Fig. 1.

The microemulsion phase varies gradually and continuously as the salinity increases. Other variables such as temperature and pressure also cause the microemulsion to gradually change properties. When the surfactant concentration is below the critical micelle concentration (CMC), no micelles form and no oil is solubilized to form a microemulsion. For surfactant concentrations below the CMC, interfacial tension is high and the surfactant is soluble in water at low salinity and in oil at high salinity. For high performance surfactants, the CMC is typically less than 0.1 wt%, thus the surfactant concentration in the water or oil is very low below the CMC. Such low concentrations are not very significant with respect to surfactant transport and utilization. However, as illustrated in Fig. 2, a discontinuity in the relative permeability occurs when the surfactant concentration either increases to values greater than the CMC or decreases to values below the CMC. Both of these changes occur when a surfactant slug is injected and then displaced by either water or polymer drive. The discontinuity at the CMC causes at most minor numerical problems because the IFT is not ultra-low as the surfactant concentration approaches the CMC for Type I or Type II phase behavior. However, the discontinuity at the CMC is significant for Type III phase behavior. This does not cause problems for typical numerical simulations because the chemical flooding process is designed so that the surfactant concentration is higher than the CMC near optimum salinity in the surfactant slug since otherwise the process fails completely.

2. New relative permeability model description

The relative permeability is modeled using Corey-type functions (Brooks and Corey, 1966) assuming the relative permeability of each phase is a function of its own saturation:(1) $k_{r l} = k_{r l}^{o} {(S_{n l})}^{n_{l}} f o r l = 1,2,3$ Where $k_{r l}^{o}$ is the endpoint relative permeability of phase $l$ , $n_{l}$ is the Corey exponent for phase $l$ and $S_{n l}$ is the normalized saturation for phase $l$ defined as:(2) $S_{n l} = \frac{S_{l} - S_{r l}}{1 - \sum_{1}^{n_{p} = 3} S_{r l}} f o r l = 1,2,3$ where $S_{l}$ is the saturation of phase l and $S_{r l}$ is the residual saturation of phase l. The most fundamental parameters in the model are the residual saturations. Residual saturations typically approach zero at high trapping numbers. However, non-zero values can be input in the model to allow for exceptional cases when one or more of the residual saturations approaches a small but nonzero value at high trapping number. The trapping number (NTl) for phase l is defined as (Delshad et al., 1996):(3) $N_{T l} = \frac{| \vec{\vec{k}} . (\vec{\nabla} p_{l'} - g ρ_{l} \vec{\nabla} D) |}{σ_{l l'}} f o r l = 1,2,3$ where $\vec{\nabla} p_{l'}$ is the pressure gradient for the displacing phase l', g is the gravitational acceleration constant, $\vec{\vec{k}}$ is the permeability tensor, D is depth, $ρ_{l} a n d ρ_{l'}$ are fluid densities and $σ_{l l'}$ is the interfacial tension between phases land l’. Below the CMC, the IFT between water and oil is used in Eq. (3). Then, the residual saturations are computed from the trapping number (Delshad et al., 1996) from Eq. (4):(4) $S_{r l} = \min [S_{l}, (S_{r l}^{h i g h} + \frac{S_{r l}^{l o w} - S_{r l}^{h i g h}}{1 + T_{l} N_{T l}})] f o r l = 1,2,3$ where $S_{r l}^{l o w}$ and $S_{r l}^{h i g h}$ are residual saturations of phase l at low and high trapping numbers. Tl is the trapping parameter for phase l.

Above the CMC, the interfacial tension between the water (l = 1) and microemulsion (l = 3) and between the oil (l = 2) and microemulsion (l = 3) are calculated from the Huh equation (1979) using solubilization ratios. These IFT values are used to calculate the water and oil trapping numbers using Eq. (4) for types I, II, and III microemulsions. When three phases are present, there are two IFT values. The microemulsion trapping number is calculated using $σ_{23}$ if $C_{23}$ <0.5 and $σ_{13}$ if $C_{23}$ >0.5. The procedure can be summarized as follows:(5) ${\begin{cases} I f C_{s u r f} < C M C \Rightarrow {\begin{cases} l = 1 t h e n σ_{l l'} = σ_{12} \\ l = 2 t h e n σ_{l l'} = σ_{12} \end{cases} \\ o r \\ I f C_{s u r f} > C M C \Rightarrow {\begin{cases} l = 1 t h e n σ_{l l'} = σ_{13}; (l' = 3) \\ l = 2 t h e n σ_{l l'} = σ_{23}; (l' = 3) \\ l = 3 t h e n σ_{l l'} = \max (σ_{23}, σ_{13}); (l' = 2 o r 1 d e p e n d i n g o n C_{23}) \end{cases} \end{cases}$

In the new model, the microemulsion parameters are calculated by interpolating between the water and oil parameters using the volume fractionof oil in the microemulsion ( $C_{23}$ ) as shown in Eqs. (6)–(8). The microemulsion parameters approach water values as the oil concentration in the microemulsion approaches zero, and they approach oil values as the water concentration approaches zero. This approach ensures the relative permeability will be continuous above the CMC whereas discontinuities could occur in the old model.(6) $S_{r 3}^{Ω} = S_{r 1}^{Ω} + C_{23} (S_{r 2}^{Ω} - S_{r 1}^{Ω}) Ω = h i g h o r l o w t r a p p i n g n u m b e r$ (7) $k_{r 3}^{o, Ω} = k_{r 1}^{o, Ω} + C_{23} (k_{r 2}^{o, Ω} - k_{r 1}^{o, Ω}) Ω = h i g h o r l o w t r a p p i n g n u m b e r$ (8) $n_{3}^{Ω} = n_{1}^{Ω} + C_{23} (n_{2}^{Ω} - n_{1}^{Ω}) Ω = h i g h o r l o w t r a p p i n g n u m b e r$

The concept captured in equation (6), (7), (8) is that the microemulsion relative permeability varies continuously between a water-rich microemulsion (low $C_{23}$ ) similar to the aqueous phase at low IFT and an oil-rich microemulsion (high $C_{23}$ ) similar to the oil phase at low IFT, but there is no derivation involved. We will observe an excellent fit of the experimental coreflood data using this model in the numerical simulation section. The microemulsion phase trapping parameter is also interpolated between water and oil parameters using $C_{23}$ :(9) $\ln T_{3} = \ln T_{1} + C_{23} (\ln T_{2} - \ln T_{1})$

The endpoint relative permeabilities are interpolated using the residual saturations:(10) $k_{r l}^{o} = k_{r l}^{o, l o w} + (\frac{S_{r l'}^{l o w} - S_{r l'}}{S_{r l'}^{l o w} - S_{r l'}^{h i g h}}) (k_{r l}^{o, h i g h} - k_{r l}^{o, l o w}) f o r l = 1,2,3$

Similarly for the Corey exponents:(11) $n_{l} = n_{l}^{l o w} + (\frac{S_{r l'}^{l o w} - S_{r l'}}{S_{r l'}^{l o w} - S_{r l'}^{h i g h}}) (n_{l}^{h i g h} - n_{l}^{l o w}) f o r l = 1,2,3$

Fig. 3 shows the step-by-step procedure for calculating the two and three-phase relative permeability values in the simulator. The smooth behavior of the relative permeability as water or polymer drive displace a microemulsion and the surfactant concentration eventually decreases to below the CMC can be explained in part as follows. As the surfactant concentration decreases from above the CMC, the oil solubilized in a Type I microemulsion decreases faster than the surfactant concentration, the oil solubilization ratio decreases, the IFT calculated from the Huh equation increases and the trapping number approaches a low value corresponding to the waterflood value. Thus the calculated relative permeability approaches the low trapping number value for water.

In the old model, the residual microemulsion saturation, microemulsion endpoint relative permeability and microemulsion Corey exponent were calculated from Equations (3), (10), (11) using microemulsion parameters at low and high trapping numbers. This required the user to input values for microemulsion parameters at both low and high trapping number for a total of six parameters that are not needed in the new model since the values are now calculated from Equation (8), (9). Experimental data show that at very high trapping number the microemulsion residual saturation approaches zero and the microemulsion relative permeability endpoint and Corey exponent are both approximately 1, so these values are typically used as defaults in simulation studies. The same approach is adopted here, and this further reduces the number of model parameters to 8.

Coreflood experiments to test chemical solutions are typically done using the following flooding sequence: (1) the core is flooded with brine (2) oil is injected at low trapping number to steady state and the oil endpoint relative permeability measured at residual water saturation (3) brine is injected at low trapping number to steady state and the water endpoint relative permeability measured at residual oil saturation (4) chemical solutions are then injected. The second and third floods provide four parameters at low trapping number (high interfacial tension). The unsteady state pressure data measured during the water-flood can be used to estimate the water and oil exponents at low trapping number by history matching the results. The only remaining parameters are then the oil and water trapping parameters, which are often known from previous capillary desaturation experiments, but otherwise must be measured in a separate experiment on the same or similar core. Thus, relative permeability experiments using microemulsion/oil, microemulsion/water or microemulsion/oil/water phases are not required to estimate any of the parameters in the new model. It is still desirable to have such data, but since they are rarely measured, it is a huge advantage to have a model that does not require them. Fortunately, the simulation results are not sensitive to the microemulsion relative permeability since it is nearly always close to a straight line due to the high trapping number. The model parameters can also be verified by comparisons between oil recovery data and numerical simulations of those experiments as shown in Fig. 3.

3. Numerical simulation results

The five simulation cases listed in Table 1 were used as test cases.

Table 1. Summary of simulation Cases.

Case	Description	Phases
Case-1	Constant salinity below optimum salinity range	Oil/Type I microemulsion
Case-2	Constant salinity above optimum salinity range	Water/Type II microemulsion
Case-3	Reverse salinity gradient	Oil/water/Type I and Type III
Case-4	Normal salinity gradient	Oil/water/type I, Type II, and Type III
Case-5	Validation of new model against ASP coreflood data

For the first four cases, a vertical coreflood was simulated using a 1 × 1 × 100 grid. The gridblock sizes are 0.109 ft × 0.109 ft × 0.00984 ft in the x, y, and z directions, respectively. The most important input parameters are presented in Table 2, Table 3. The porosity is 0.25 and the permeability is 200 mD. The initial oil saturation is 0.4, which is equal to the residual oil saturation at low trapping number.

Table 2. Phase behavior input data for surfactant properties.

CMC	0.0001 [vol/vol]
Lower Type III salinity	0.970 [meq/ml]
Upper Type III salinity	1.200 [meq/ml]
Height of binodal curve at 0, 1 and 2 times optimal salinity	0.1, 0.03, 0.1

Table 3. Relative permeability parameters at low and high trapping numbers.

Properties	Old Model	New Model
$S_{r w}^{l o w} / k_{r w}^{l o w} / n_{w}^{l o w}$	0.3/0.045/3.0	0.3/0.045/3.0
$S_{r o w}^{l o w} / k_{r o}^{o, l o w} / n_{o}^{l o w}$	0.40/0.90/1.5	0.40/0.90/2.5
$S_{r M E}^{l o w} / k_{r M E}^{o, l o w} / n_{M E}^{l o w}$	0.35/0.4/2.25	Not used

$S_{r w}^{h i g h} / k_{r w}^{o, h i g h} / n_{w}^{h i g h}$	0.0/1.0/1.0	0.0/1.0/1.0
$S_{r o w}^{h i g h} / k_{r o}^{o, h i g h} / n_{o}^{h i g h}$	0.0/1.0/1.0	0.0/1.0/1.0
$S_{r M E}^{h i g h} / k_{r M E}^{o, h i g h} / n_{M E}^{h i g h}$	0.0/1.0/1.0	Not used

$T_{w} / T_{o} / T_{m e}$	2500/5000/3500	2500/5000/Not used

Oil and water relative permeability parameters at high and low trapping numbers are given in Table 3. For all four cases, a 0.2 PV SP slug with a surfactant concentration of 0.5 v% and a polymer concentration of 0.35 wt% was injected at 0.0015 ft3/day followed by a polymer drive at the same flow rate.

Case-1: Simulation of Type I Microemulsion: For Case 1, the initial, slug and polymer drive salinities were all equal to 0.9 meq/ml, which is below the lower Type III salinity of 0.97 meq/ml. Therefore, the microemulsion is always Type I. Fig. 4 compares the saturation and relative permeability profiles at 0.5 PV. The old model resulted in discontinuities in the simulated relative permeability whereas the new model is continuous. For the old model, the oil relative permeability decreases discontinuously at a distance of 0.2 ft from the outlet whereas it increases smoothly when the new model was used for the simulation. Also, the simulated microemulsion relative permeability is continuous with the water relative permeability at the CMC when the new model is used. The microemulsion relative permeability is continuous with the water relative permeability depicted by the blue curve in Fig. 4.

Fig. 5 compares the pressure and the oil trapping number profiles at 0.5 PV. The trapping number shows a discontinuity using the old model, but the new model is continuous. Fig. 6 compares the average pressure and oil cuts. The difference in the oil cut is significant indicating the discontinuity in the old model can make a significant difference in the oil recovery results in addition to causing numerical problems.

Case-2: Simulation of Type II Microemulsion: For Case 2, the initial, slug and polymer drive salinities were all equal to 1.33 meq/ml, which is greater the upper Type III salinity of 1.2 meq/ml. Therefore, the microemulsion is always Type II. Fig. 7 compares the relative permeability profiles at 0.5 PV. The old model shows a discontinuity although it is less than for Case 1. The new model is continuous at the CMC where the microemulsion and oil relative permeability are the same.