Reactive power control of three-phase low voltage system based on voltage to increase PV penetration levels

1. Introduction

The world continues to demand electric energy, and on the other hand the traditional energy, introduces pollution as carbon taxes. The green energy provides promotion [1].

It is expectant that future LV networks will help for high penetration levels of small-scale PV. The high penetration of PV Power may cause several problems, such as voltage fluctuations, encumbering of grid appliances, harmonics currentradiations grid thinking, flicker, direct current injection…, etc. [2], [3].

This study focuses on the grid voltage to keep it inadmissible limitations, especially in the case of reduction in the power demands with high active power injections by PV inverters.

In Egypt, the traditional electricity demand is growing rapidly, especially the residential loads (42.7%) and the industrial loads (27%) of the total energy [4]. So, the Egyptian government forwards its efforts direct to integrate dispersed generators, especially for residential power demand of small-scale PV up to 10 kW. In addition, Egypt has the best locations with high intensity of direct solar radiation, the range was between 2000 and 3200 kW h/m2/year from north to south, and the sun shines duration was between 9 and 11 h/day [5]. So the Egyptian government, has approved the fed-in tariff and subsidized the customers and investors to promote the PV penetration levels.

The main purpose of this paper was to increase the penetration attribution of PV power producing in three-phase LV network-connected in Egyptian networks, by controlling of reactive power capability, which is generated from the solar inverter and P.F- P. in this paper the control of PV inverter is implemented using proportional plus integral (PI) controller to maintain the voltage at the PV bus.

2. Reactive power supply capability of basic concepts in analysis of distributed generators

To increase the higher penetration levels to the power distribution systems, it may require a lot of efforts, to integrate dispersed generators. The optimum benefits from solar inverters installed on grid were to promote penetration levels more. The semiconductor switches are control of the Q quantity of inverter. When the active power injection is less than the inverter rated apparent power, the remaining capacity can be used for supplying reactive power. New generation of solar inverters power factor (PF) is set at 0.9 PF, which keeps them at rated active power injection for network ancillary services. Reactive power can control the grid – connected inverters on LV distribution networks [6]. As a toss network cryptogram, the minimums P.F value is set at 0.9 by the control of the loll encyclopedia in the sequence that could be acclimated in the Egyptian grid code. In addition to this, if the solar irradiationdecreases from 100% to 10%, the inverter can use the remaining capacity to provide the reactive power supply to compensate the voltage drop [7].

Further, the grid voltage levels must be defined clearly as the power injections from the distributed generators, cause rise in the total voltage on the LV and MV grids which should be finite at ±10% and ±5% of the nominative grid voltage, consecutively. Thus, at apiece bond speck, it is required to measure these voltage changes that are triggered by the generators, where maximally permissible power injecting is specifiable. Thus, the following conditions can be realized:

1.
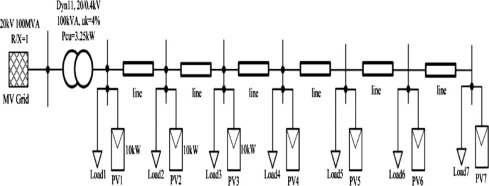
Unlimited number of inverters can be connected to the same transformer, with considering the full loading that is 100%. Fig. 1 shows the structure of network and installed inverters location, depending on adaptive Q and V method [8]. To control higher voltage drop at the end of the feeder, this method is based on the voltage sensitivity analysis measurements.
1. Download : Download high-res image (72KB)
2. Download : Download full-size image
Fig. 1. Network feeder for the voltage gradient.
2.
The inverters should have coordination among each other and with the equal distance (100 m), to work in the acceptable network voltage without a communication medium.
3.
All the PVS installation capacity is 10 kW at the same time.

3. Inverter controller

Fig. 2 shows that, at the network-side inverter, a back-to-back remitted, the phase angle of the current to the primate grid is defined. In the DC - DC converter is used for maximum power point tracking. Moreover, the grid side inverter is used to control both of the DC link voltage and the voltage at the point of common coupling (PCC). The three-phase voltage at the PCC is sensed and follows a phase locked loop (PLL) circuit to generate the transformation angle. The actual three- phase currents at the PCC are converted from the abc to dq0 frames. The proportional plus integral (PI) controllers are used for this control action and produce the firing angles to the power electronic switches of the inverter.

The output voltage of inverter can also be adapted by applying a controller itself in the inverter. Most commonly used method for the inverter is the sinusoidal pulse width modulation (PWM) technique. By implementing this method, a constant DC input voltage is disposed into the inverter. Also an unflappable AC output voltage is accessed by regulating the on/off duration of the inverter units, PWM techniques [9].

The phase shift of the current vector can be arbitrarily controlled as long as the absolute value of the current. Appendix A shows that the relation between phase shift and voltage (θ ° limits 17.44–30.34 with active and reactive power can be considered). The power commute Pact (within its boundary Pmin and Pmax) during the inverter is in general dealt by the executive control of the PV system with first imperative so that its boundary is the maximum possible reactive power preparation |Q|max in Eq. (1).(1) $| Q |_{max} (t) = \sqrt{s_{\max}^{2} - p_{act}^{2} (t)}$ The current faces accessorial boundary Qmin and Qrnax essentiality due to causes of stability and availability. The executive purview (uploaded receptivity) of an inverter is shown in Fig. 3. Within these limitations, the reactive power of the inverter can be controlled with response to these limits as shown in Appendix B(Pmin = 2.5 and Pmax = 10 KW), (Qmin = 0 and Qmax = 10 KVAR).

4. Simulation results

The inverter is simulated by MATLAB Simulink [10]. Results are shown. It is developed by voltage VL-L of 380 V rms.

The Simulation of power control of the PV system under environmental condition changes is shown Fig. 4.

The PCC Voltage (0.38/11 kV) is load (10 kW, 4.5 Kvar), and the PV system is compound of solar arrays.

The PV system configuration with 8 parallel connections and 5 series connections accomplishes the aspired DC power and DC voltage input for an inverter system, the PV type is monocryt line and 17.2% efficiency, and the data of the PV module are indicated in [11]. Table 5 illustrates the PV module parameters.

The maximum power of the PV arrays is around 10 kW. Simulation is done with Matlab/Simulink program.

The parameters of solar module at 25 °C which used in the simulations are listed in Table 1.

Table 1. The solar module's, parameters at 25 °C.

Imp (current at MPP)	7.7098 A
Vmp (voltage at MPP)	35 V
Pmax (maximum electrical power)	270 w
VOC (open circuit voltage)	44.4999 v
Is.c (short circuit current)	8.1998 A

The results of simulation for the proposed PV unit based on I-V and P-V clc's are shown in Fig. 5a, Fig. 5b.

The results of PV module based on P-V and I-V clc's at different values of cell temperatures and irradiations are shown in Fig. 6a, Fig. 6b.

Voltage analyzed can rim the supernumerary influential locations and require quantities, to serve reactive power for the grid voltage support from the distributed solar inverters. Assume that the 8- bus radial pretest feeder has three – phase balancing power stream as shown in Fig. 1.

The 8- bus radially test feeder is utilized measurements of the different values of the parameters for load flow calculations. It shows the values of voltage regulation for the grid voltage (Vg) and the load voltage (VL) for each PV location of the grid. These data depend on the connection points of the inverters, that are closest and faraway of the transformer, while neglects the power demand from the consumers.

Fig. 7, shows the voltage values before PVs installation.

Table 2 shows the values of voltage regulation (ε) for Vg and VL at each PV location of the grid. Eq. (2) estimates the voltage regulation (ε) values for each location.(2) $ε = \frac{V_{g - V_{L}}}{V_{g}}$ Fig. 8 shows the voltage values after installation of PVs, and the variation of ε values was based on measurements of voltages before PVs installation.

Table 2. Voltage values before installation of PV for v1–v7.

V1	V2	V3	V4	V5	V6	V7
0.0%	2.7%	4.1%	5.6%	8.6%	10.89%	15.7%

Table 3 shows the enhancement of measurements for the voltage values after the installation of PVs without control of reactive power with the distance between the inverter and transformer

Table 3. Voltage regulation values after installation of PV for V1–V7 Before control of Q (u).

V1	V2	V3	V4	V5	V6	V7
0%	1.3%	2.7%	4.1%	5.6%	7%	8.6%

Fig. 9, shows the voltage values after control by reactive power to compensate VD.

Table 4 shows the voltage rise due to the converted part of the real power (mi), produced from V1 to V7 to reactive power, to compensate the voltage drop that increases with the distance from the transformer. With the set valuable of PF, this finitely reactive power spotting can still profoundly furnish supplemental voltage drops on the transformer and the outlines. From the voltage analysis the lower PF values could be appropriated to the inverters, which are connected to the transformer, to obtain the optimum voltage values in admissible rate imposed by certain grid codes as shown in Table 5. The required PF can be determined for each inverter as shown in Eqs. (3), (4).(3) $Δ U = S_{UP} . Δ P + S_{UQ} . Δ Q = 0$ (4) ${PF}_{i} = \frac{1}{\sqrt{1 + m_{i}^{2}}}, m_{i} = \frac{S_{UP} (j, i)}{S_{UQ} (j, i)}$ where SUP, SUQ, PFi and mi respectively, are the voltage sensitivity to active power, the voltage sensitivity reactive power, PF and mi required at i th bus. In addition to this ίth corresponds to the bus code at the PVs coupling point in this case, as shown in Fig. 6a, Fig. 6b 10 kW of constant active power injection (P = 10 kW) appropriated to all inverters instatauts time, and the required PFs to keep the voltage level until bus 7 inadmissible limitation [12].

Table 4. The reactive power and the PF values set for each inverter.

mi	0.1	0.2	0.25	0.3	0.35	0.4	0.46
PF PVI	0.99	0.98	0.97	0.95	0.94	0.92	0.9
Q KVAR	1	2	2.5	3	3.5	4	4.6

Table 5. Voltage regulation values after control of Q (u) & cos φ (P) to PV1 – PV7.

V1	V2	V3	V4	εV5	V6	V7
0.0%	0.0%	0.53%	0.8%	1.1%	1.3%	2.7%

Fig. 10 illustrates the simulation results of the system in the case of without V1, with V7, and with PV and Q control.

Fig. 11, shows the voltage drop of the system for three cases :-

1.
without P.V
2.
with P.V and without Q controlled
3.
with P.V and Q controlled