1. Introduction
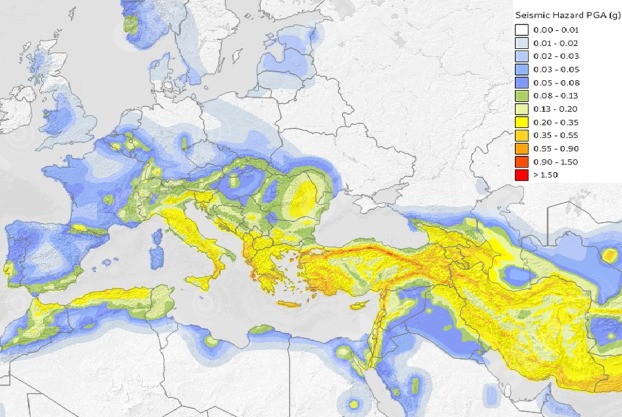
In the past few decades, natural catastrophes, including earthquakes, have led to a dramatic increase in human and economic losses. A loss model for earthquake risk is required to predict the economic impact of future risks as well as to define risk mitigation plans by national authorities [1], [2]. Seismic vulnerability assessment, which describes the susceptibility of a structure to damage due to ground shaking, is a pivotal part of a loss model [3], [4]. Masonry buildings can be considered as the oldest construction type and represent a large part of the building portfolio in high seismicity zones. Fig. 1 presents a hazard map of the high seismicity zones in Europe and the Middle East based on the peak ground acceleration (PGA) of the area. Fig. 2 illustrates the ratio of the number of unreinforced masonry (URM) buildings compared to other types of structural systems in European countries, as well as the number of all buildings in each country [5]. URM is considered as a prevalent structural system in high seismicity zones, i.e., Italy, Greece, Bulgaria, Turkey, as depicted in Fig. 2, and Iran based on [6].
 Fig. 1
Fig. 1 Fig. 2
Fig. 2Fig. 3 (a) shows a hazard map of South America, and as illustrated in Fig. 3 (b), the prevalent construction type is URM. Fig. 3 (b) also shows the distribution of URM buildings, the number of all buildings (in millions), and the replacement cost for each country. The replacement cost is the value of replacing a constructed building based on the latest seismic code in a country [8].
 Fig. 3
Fig. 3URM buildings are characterized by a high seismic vulnerability; in fact, both the mortar and the masonry unit are known to be “quasi-brittle materials” whose mechanical performance could be deteriorated under seismic loadings. Due to the absence of a robust connection between structural components and insufficient stiffness of horizontal floors, URM buildings are highly susceptible to lateral cyclic loads that involve the out-of-plane bending behavior of walls and combined in-plane and out-of-plane collapse mechanisms [10], [11], [12].
Fig. 4 shows a seismic risk map of two susceptible zones where URMs are prevalent construction buildings. The reported average annual loss (AAL) in some parts of the high seismicity zones with high PGA is more than 5,000 USD per m2, representing a severe economic loss for governments [13].
 Fig. 4
Fig. 4Based on the statistics from several earthquakes (1886–2003) in the United States, 20% of 4,457 URM buildings were either partially damaged or completely collapsed, and the reason for collapse for 83% of the damaged buildings was the brickwork fell [15]. As shown in Fig. 5, due to the vulnerability of this structural system, the construction of the new buildings made of URM is not permitted in some states of the United States [15].
 Fig. 5
Fig. 5In order to decrease human and economic losses, seismic vulnerability assessment of URM buildings is needed by national authorities at different scales. Different historical URM structures with complex architecture need to be preserved, as do existing vernacular URM buildings. In recent decades the resiliency of structures and infrastructures has attracted wide attention, and in order to facilitate a resiliency framework, a robust vulnerability assessment methodology is required to be applied at a large scale [16]. The methods should be user-friendly due to the high number of archetypes as well as be fast in computation [16], [17]. Therefore, as illustrated in Fig. 6, the scale of vulnerability assessment procedures can be classified into three groups ranging from building scale to large scale [18].
 Fig. 6
Fig. 6Different seismic vulnerability assessment methods have been proposed in the literature and can be divided into three main groups: (1) empirical methods (EM), (2) analytical methods, and (3) hybrid methods (HM) (see Fig. 7). The most common methods for the seismic vulnerability assessment of building typologies at different scales aim to define a damage probability matrix [19] or fragility curves [20].
 Fig. 7
Fig. 7EMs are based on visual inspection of buildings in the post-emergency phase and damage data obtained from observed past earthquakes [21], [22], [23], [24], [25]. They refer to typological building classes or vulnerability indexes and can be correlated with construction techniques, types of materials, and different building features [26], [27], [28], [29], [30], [31]. A limitation of these methods is their validity that can be limited to specific geographical and seismic regions [32].
Analytical methods require detailed vulnerability assessment algorithms to consider the physical and mechanical properties of buildings that can be calibrated to various characteristics of building stocks and hazards [33]. However, deriving analytical vulnerability curves is time-consuming and needs high computational effort. Consequently, basic users cannot easily develop curves for different areas or countries with diverse construction characteristics [3].
HMs are a combination of EMs and analytical methods whereby post-earthquake loss data is combined with results from analytical methods of a building typology [34], [35]. Visual inspection data reduces computational efforts of analytical methods. Furthermore, HMs and EMs are utilized for calibrating the analytical methods [3].
Analytical methods can be divided into two sub-groups: detailed analytical methods (DAMs) and simplified analytical methods (SAMs). DAMs for the seismic vulnerability assessment of URM buildings comprise a sophisticated, detailed numerical simulation by conducting nonlinear analyses [36]. Different methods have been presented for nonlinear analysis of URM buildings in order to show their actual behavior when subjected to seismic loads. Nonlinear static (pushover) analysis (NSA) is the most popular method, where the lateral static load is applied to the model and is increased until a displacement target is reached [37]. Incremental dynamic analysis (IDA) is the most advanced type of detailed analysis, in which accelerograms are applied to the building model, and their intensity increased until the collapse occurs [10], [38].
In order to reduce time consumption and computational effort, different simplified analytical methods (SAMs) for the seismic vulnerability assessment of URM buildings have been developed. Collapse mechanism-based (CMB) methods are based on the kinematic chain in order to derive the collapse multipliers for different probable collapse mechanisms of URM buildings subjected to a given intensity of a seismic record. Capacity curves are the result of the NSA. In capacity spectrum-based (CSB) methods, a predetermined capacity curve is computed for each building typology. The capacity curve is then intersected with the seismic demand to derive the performance points in different damage thresholds. In fully displacement-based (FDB) methods, an equivalent single-degree-of-freedom (ESDOF) model of a building is derived, and the displacement capacity for each damage threshold is compared to the displacement demand in each corresponding period of vibration in order to derive the possibility of crossing the damage thresholds [3], [17], [32].
When dealing with a single-building assessment, uncertainties are mainly due to the lack of expert knowledge of the structural features, which can be reduced by an on-site survey [39]. However, when dealing with vulnerability assessment at a large scale using the SAMs, a broad range of variables and a great deal of uncertainty are involved in both the modeling process and parameters [40], [41]. Generally, uncertainty on capacity, demand, and damage thresholds are the sources that are identified by most of the available seismic vulnerability assessment methods [42].
Fig. 8 presents a schematic overview of the scale of assessment and the complexity level of the analysis methodologies. As shown, the complexity and time consumption level increase from the green area to the red area, where the highest level is related to the IDA of detailed nonlinear models of all the buildings at a large scale, which is uncommon nowadays. Moreover, EMs requiring the lowest computational effort are not suitable for the seismic vulnerability assessment of single-building but only for the building stock scale and large scale. The yellow area shows the methods that nowadays are most commonly applied to a specific case study scale.
 Fig. 8
Fig. 8The aim of this paper is to provide a state-of-the-art review of the developments of the SAMs, which are categorized and illustrated in a black box in Fig. 8. The complexity and corresponding computational efforts of each method are investigated by emphasizing their mechanics basis, drawbacks, and advantages. Note that the main focus of this paper is on unreinforced brick masonry buildings; however, case studies about stone and adobe masonry have been addressed to present the operational scope of each method. Moreover, particular attention is given to different software packages that were developed to facilitate the application of the SAMs for the seismic vulnerability assessment of URM buildings by investigating their strengths and weaknesses.
2. Collapse mechanism-based methods
The main concept of CMB methods is to assess the vulnerability of URM buildings by defining predefined collapse mechanisms or decomposing them into rigid macroblocks. In CMB methods, first, collapse multipliers are computed, and the minimum value is defined. Then, the corresponding collapse mechanism is considered as the most critical mechanism.
VULNUS is one of the CMB methods proposed by Bernardini et al. [43] based on in-plane and out-of-plane collapse mechanisms of URM buildings. In this method, the collapse multipliers are derived from the ratio of shear strength and flexural of walls for in-plane and out-of-plane collapse mechanisms of URM walls by applying the virtual work principle according to the static theorem of limit analysis [44]. A comparative seismic assessment has been done for URM building aggregates within the historical center of Arsita damaged by the L’Aquila earthquake (2009, April 6th) in Italy [45]. A macroseismic EM was utilized to derive the vulnerability indexes and the corresponding fragility curves. Furthermore, the VULNUS method was used to derive the fragility curves. Within the VULNUS method, the terms I1 and I2 take into account the probable in-plane and out-of-plane mechanisms. Moreover, DAM was done by means of an equivalent frame method embedded in 3Muri software [46]. Detailed three-dimensional (3D) models were provided, NSA was done, which is described in detail in [47], and by means of the CSB method, the corresponding fragility curves have been derived. This study shows that the fragility curves derived from the VULNUS method are placed in the middle range between the upper limit (conservative) DAM and the lower limit ones derived from the EM of the fragility domain [45].
Performance-based assessment and the seismic risk mitigation of cultural heritage assets were incorporated into the Italian guidelines (PCM) [48] outlined by the Italian building code [49]. For this purpose, a CMB method was added to and recommended by the Italian guidelines [36]. Some of the predefined collapse mechanisms in the PCM are illustrated in Fig. 9 [50], [51].
 Fig. 9
Fig. 9Using SAMs associated with an ESDOF modeling of buildings is not reliable enough for global evaluation of URM cultural heritage sites with complex architecture. Therefore, investigating the local mechanisms using the CMB methods is needed to be done. Not only the predefined collapse mechanisms but also the lack of connections with the orthogonal walls, infinite compression resistance (rigid blocks), and zero tensile resistance strength are the simplified hypotheses considered in this type of analysis [52].
A damage assessment was done for the churches after the L’Aquila earthquake (2009) using the PCM method, see [53]. Totally 28 predefined collapse mechanisms were considered to cover all the collapses that may occur for the macroelements of the churches such as façade, nave, transept, triumphal arch, dome, apse, roof covering, chapel, and bell tower. According to this study, seismic behavior evaluation of the URM churches using the PCM method has been proven as a rapid and reliable method. Moreover, it was concluded that the substitution of timber roofs with reinforced concrete (RC) slabs cause an increase in mass and stiffness, which produced negative effects on the behavior of the churches that should be avoided as a restoration method in the future [53].
The mentioned CMB methods were then developed by importing the actual 3D geometry by considering the irregularities of the masonry towers to assess the susceptibility of them subjected to different distributions of horizontal loads [54]. Five predefined collapse mechanisms, including rocking, Heyman’s diagonal cracking, and base shear sliding, were hypothesized for the kinematic limit analysis (KLA) of the towers in [55], and an optimization algorithm was embedded to minimize the failure multiplier of each mechanism.
The 3D KLA-based method was applied to two URM towers, and the results were compared with the results of nonlinear static and dynamic analyses of the detailed finite element models (FEMs). The method is believed to be considered a reliable tool for most cases; however, increasing the number of failure mechanisms such as rocking on the upper corners or the collapse of the belfry can increase the method's accuracy [54].
The possibility of importing the actual 3D geometry of the case study and applying different distributions of horizontal loads are considered as the two main advantages of the 3D KLA-based method for the URM towers that can be expanded to be used for the assessment of URM building aggregates. Nevertheless, computing the collapse multipliers for the predefined collapse mechanisms is a limitation in the proposed KLA methods. To address this limitation and decrease the level of uncertainties related to modeling and capacity, mentioned CMB methods were developed by modeling the structures with rigid macroblocks considering indefinite collapse mechanisms [36].
The application of the CMB method for predicting the masonry domes' failure behavior subjected to static horizontal loads has been investigated in [56]. The dome was modeled by means of a few rigid non-uniform rational basis spline (NURBS) elements, with the hinges at the element edges forming the failure mechanism. KLA was performed on a NURBS model and compared with the results of the NSA of a detailed FEM, and the ultimate load factors were the same, which shows the reliability of this method [56].
The NURBS-based KLA method was then developed [57] to find the minimum collapse multiplier of historical URM building aggregates. In order to estimate the minimum collapse multiplier and investigate the exact position of the fracture lines, a genetic algorithm-based mesh adaptation was applied to a 3D model of the whole aggregate, modeled with NURBS surfaces.
Seismic vulnerability of one of the URM aggregates, named I1 Torrione in Arista, Italy, was assessed using different types of modeling approaches [58]. Four different structural units were chosen from the whole building and modeled using the NURBS-based KLA method to identify the local failure mechanism multipliers. Moreover, both local and global mechanisms were evaluated by performing the NSA on an equivalent frame model of the building in the 3Muri software package [46], [59]. Furthermore, the FEM of the aggregate has been provided, and the results from the NSA were compared to other methods’ results.
The evaluation of a safety factor, which is the ratio between the spectral acceleration and the maximum acceptable value has been performed for all the methods. Comparing the safety factors obtained from the analyses results of the four mentioned methods illustrates that the analyses using the equivalent frame method in 3Muri software have the largest safety factor value for the building since out-of-plane failure modes have been neglected. NSA was done on the FEM of the building with more computational effort compared to the analysis in the 3Muri software package. However, the safety factor derived from the finite element analysis is lower than the result from 3Muri since the out-of-plane collapse mechanism has been considered. Local mechanism analysis using the 3Muri software package is in the third rank with a fast and enough accurate methodology. Nevertheless, predefined collapse mechanisms have been considered. Finally, the lowest safety factor refers to the local analyses using the NURBS-based KLA method with low computational efforts and automatic mesh adaptation [58].
For the seismic vulnerability assessment of heritage URM buildings with complex architecture, that the global behavior of the structure is not guaranteed, CMB methods are recommended as a very fast and accurate enough method. Since in-situ destructive tests are rarely allowed for the heritage buildings and corresponding high level of uncertainties about structural details, several models need to be analyzed. Therefore, the FEM approach with high computational effort is not recommended.
Detail about each reviewed CMB method is summarized in Table 1, which can facilitate comparing the methods. Moreover, relevant references for some applications have been provided. Although it can be seen that for some of CMB methods (i.e., VULNUS, PCM) the in-plane collapse mechanisms have also been evaluated, the main focus of the CMB methods is to evaluate the local mechanisms occurring due to the presence of flexible diaphragms with a poor connection to the URM walls which can be observed in old buildings.
Table 1. Details about each CMB method and the relevant references for the applications.
| Method | Collapse mechanism | Data collection | Output | Brief description | References |
|---|---|---|---|---|---|
| VULNUS | 1 predefined in-plane and 1 predefined out-of-plane collapse mechanisms | On-site survey | Collapse mechanisms’ acceleration and the most probable collapse mechanisms | Computation of collapse multipliers applicable for URM small building stocks. | [44], [45], [60], [61], [62], [63] |
| PCM | 28 predefined in-plane and out-of-plane collapse mechanisms | On-site survey | Collapse mechanisms’ acceleration and the most probable collapse mechanisms | Computation of collapse multipliers applicable for URM churches or towers (at building scale). | [51], [52], [53], [64], [65], [66] |
| 3D KLA-based (Towers) | 5 predefined collapse mechanisms | On-site and 3D geometrical survey | Collapse mechanisms’ acceleration and the most probable collapse mechanisms | Deriving the most probable collapse mechanism of a 3D model applicable for URM towers (at building scale) using optimization algorithms. | [54] |
| NURBS-based KLA | Indefinite local mechanisms | On-site and 3D geometrical survey | Collapse acceleration and possible fracture lines | Deriving the most probable collapse mechanism of URM buildings’ structural components modeled with rigid NURBS elements (at building scale). | [56], [57], [58] |
2.1. Software packages
c-Sisma is a KLA-based software designed to investigate the predetermined collapse mechanism multipliers in which the material properties, wall geometry, and seismic loads are considered as inputs for the software; where the multipliers for each collapse are the outputs [67]. c-Sisma is based on predetermined collapse mechanisms specially designed for typical residential URM buildings, but some software packages were developed to investigate all collapse mechanisms and different types of structures, including arches, domes, and vaults. Brickwork is one of the CMB method software packages that includes these developments in two-dimensional (2D) environments [68] to be developed and verified by comparing to finite element analysis results [69].
A macro-block software [70] was developed for the assessment of out-of-plane behavior of URM walls based on the details elaborated by Lagomarsino [71] in the context of the PERPETUATE project [72] aimed for the performance-based assessment of cultural heritage assets. The interface software is developed and added to the 3Muri software as a module for local collapse mechanism assessment of URM walls based on the predefined collapse mechanisms that are prescribed by the user. A 3D model of a building can be defined, and the collapse mechanisms and the constraints for each component should be specified, and the corresponding collapse multipliers will be calculated based on the kinematic analysis rules [59].
UB-ALMANAC uses an adaptive NURBS-based KLA approach, which is another fast and user-friendly software for upper-bound limit analysis of URM buildings [56], [73]. The UB-ALMANAC is used for the seismic vulnerability assessment of churches by 3D modeling of the structure with rigid macro blocks joined by elastoplastic interfaces to derive the collapse multiplier and the most probable collapse mechanism. It can consider the directions of seismic loads, different mesh sizes and types, and interconnection of the walls [74]. LiABlock_3D is a MATLAB-based tool with a graphical user interface into which computer aided design (CAD) files can be easily imported, allowing high flexibility in structural configuration [75].
3. Capacity spectrum-based methods
The Capacity Spectrum-Based (CSB) Method has spread considerably in the last three decades because it can be considered a valid alternative to nonlinear time-history analysis. It was introduced in ATC-40 [76] and implemented in HAZUS methodology for earthquake loss estimation [77]. Other alternative versions of CSB methods are available in FEMA 273 [78] and the N2 method [79], [80] that is introduced nowadays in Eurocode 8-part 3 [81]. The N2 method was formulated in the acceleration – displacement format by Fajfar [80], although the original idea of this method dates back to the mid-1980s [82].
The general procedure of the CSB methods is synthesized in Fig. 10. The capacity curve of a building is derived from NSA, and then it is transformed from a multi-degree-of-freedom (MDOF) system into an ESDOF system, as shown in Fig. 10 step 1. It is recommended that capacity curves for URM buildings be fitted via a bilinear elastoplastic capacity curve as illustrated in step 2 [38]. The idealized capacity curve will be intersected with seismic demand in order to compute the performance point of the structure. The seismic demand can be evaluated by selecting the ground motion record and deriving the inelastic response spectrum that allows identifying the performance point that defines the inelastic displacement demand for a specific ground motion, as shown in Fig. 10 step 3. A set of ground motion records can be selected, and the procedure above described can be repeated for increasing ground motion intensities (e.g., Fig. 10 step 3a) up to all limit states are reached so that the earthquake demand parameters can be evaluated for each damage state and the fragility curves that represent the probability of occurrence of a specific damage state for a given seismic demand can be derived [38], [72], [80]. Alternatively, the smoothed elastic code-based spectrum can be used as shown in Fig. 10 step 3-b. However, the last alternative cannot reflect record-to-record variability; consequently, it is not recommended to develop fragility curves because it does not account for uncertainties due to ground motions.
 Fig. 10
Fig. 10Different simplified CSB methods have been proposed in literature in a way that the pushover curves are derived for a simplified model [83]. Among them, the failure mechanism identification and vulnerability evaluation (FaMIVE) method is one of the most noteworthy. It was first introduced as a CMB method by D'Ayala [84] to assess the vulnerability of historic URM buildings in town centers.
The collapse multipliers were calculated for probable collapse mechanisms by considering both in-plane and out-of-plane failures through an equivalent static procedure. Twelve probable mechanisms are identified, as shown in Fig. 11, and the most probable mechanism is associated with the lowest base shear capacity [84].
 Fig. 11
Fig. 11The specific feature of FaMIVE is strictly related to how the data collection is organized by on-site inspection, concentrating on those parameters that can directly qualify the seismic performance of URM buildings and can mostly be surveyed from a rapid visual screening.
The buildings are classified with approximately the same typological layouts, masonry fabrics, and quality of materials. Data collection by performing the on-site inspection is the preliminary step of the FaMIVE method to collect specific information for each building, such as height, length, the thickness of each accessible façade, number of stories, strengthening devices, etc. It is possible to input on-site survey data electronically, which is automatically stored in the database sheet to calculate the failure load factors.
Based on the information collected, the ultimate load factor of each external wall for each collapse mechanism is calculated. The collapse mechanism for a given façade depends on the type of connections to the rest of the structure, mainly due to the type of horizontal structures, because if the floor is not rigid in its plane, like vaults or wood floors, it affects the redistribution due to a seismic action that depends from the connections with internal walls and position of the timber beams or vaults. The lower mechanism in terms of collapse acceleration is the most probable one, selected to calculate the fragility curves [85] that can directly be obtained from the collapse accelerations, as illustrated in Fig. 12 with the first alternative.
 Fig. 12
Fig. 12Then this method was extended from a purely CMB method into a CSB method [32], [86]. For each failure mechanism, a specific capacity curve is defined with the aim to define fragility curves. The reliability of the procedure is strictly connected to the idealized capacity curves of the ESDOF model and to the selected limit states. In particular, the authors use the NSA by means of the N2 method, as proposed in Eurocode part 3 [81], where the performance point is evaluated using a degrading pushover curve. This procedure is illustrated in a simplified way in Fig. 12, alternative 2. The capacity curve can be computed and intersected to the acceleration-displacement seismic demand spectra to define performance points. Fragility curves are then developed from performance points for each building typology [87], [88], [89].
Four limit states have been considered for the FaMIVE method based on the pushover curve. Damage limitation (DL) corresponds to the ultimate elastic capacity, significant damage (SD) corresponds to the first peak capacity point, near collapse (NC) limit state corresponds to the maximum displacement without shear resistance degradation, and the collapse (C) limit state corresponds to the ultimate capacity point. The corresponding computed inter-story drifts ratio (IDR) of the mentioned limit states have been summarized in Table 2.
The FaMIVE procedure allows the retention of a high level of detail of the geometry and kinematics of the problem. Simultaneously, since it computes only the ultimate condition, it does not require the computation or time demands of a typical NSA [38].
Uncertainties related to damage thresholds, capacity, and demand have been considered in the FaMIVE method, which are effective on fragility curves. Furthermore, epistemic uncertainties concerning the reliability of input data from the on-site survey form have been contemplated [32].
The FaMIVE method has been utilized for the seismic vulnerability assessment at a large scale for Casbah of Algiers in Algeria [90] in the context of Perpetuate project [72]. First of all, significant building typologies have been identified evaluating the seismic performance of these selected buildings in terms of lateral capacity and collapse mechanisms. Different intervention recommendations were proposed to enhance the Algerian construction quality [90].
The European Commission launched the RISK-UE project [91] in seismic risk analysis, concentrating on the distinctive features of European cities regarding modern and historical buildings [92]. For this purpose, Lagomarsino [93] presented a mechanical procedure for the seismic risk assessment of both URM and RC frames, which was proposed in the framework of the RISK-UE project.
This method uses simplified bilinear capacity spectra, derived depending on the building typology's geometrical and characteristics, including the number of floors, material properties, drift capacity, and timespan of construction. Moreover, for URM buildings designed without any seismic criteria, a prevailing collapse mode is defined based on the method presented in [94]. The uniform collapse mode or the soft-story collapse mode due to rocking or shear failures has been considered, while the out-of-plane mechanisms have been neglected.
By assuming a bilinear representation, the capacity curve is identified in terms of yield spectral displacement and acceleration (dy and ay respectively) and ultimate spectral displacement and acceleration (du and au, respectively) points. In the further hypothesis to neglect hardening behavior, capacity curves can be defined by three parameters: the yield acceleration ay, the fundamental period of the building T, and the structural ductility capacity μ.
The authors proposed a set of European building typology classifications for masonry and RC buildings. In particular, for URM buildings, they introduced six typologies for URM and one typology for reinforced masonry buildings. For each of them, different types of horizontal structures have been considered: wood slabs, masonry vaults, composite steel and masonry slabs, and reinforced concrete. Moreover, three possible intervals have been considered for the number of stories: low-rise with 1–2 stories, mid-rise with 3–5 stories, high- rise with more than six stories. For each building typology, the parameters that define the capacity curves are presented in a table, with the great advantage that the user can directly consider the capacity curve proposed by the authors, and it is not required to model the building. In this approach, once capacity spectra are derived for the building classes, the next step is to use the CSB method. The performance point of each building class is obtained by intersecting the capacity spectrum with the inelastic acceleration-displacement response spectrum, which is produced by using codified spectral shapes calibrated to the PGA obtained from the hazard analysis. Four damage states were considered in order to investigate the level of damage, which can be derived from predefined equations based on the yielding dy and ultimate du displacements [93].
In the context of the RISK-UE project, the seismic risk evaluation of about 60,000 residential buildings in the city of Barcelona in Spain was done using the simplified mechanical method [93]. In particular, six-building classes were considered to develop two damage scenarios realized for deterministic and probabilistic seismic hazard. It was concluded that URM buildings show higher vulnerability compared to RC building typologies. Moreover, maximum damage values were expected for high-rise URM buildings located on soft soils [95].
Pagnini et al.[96] proposed an analytical method to assess the vulnerability of masonry buildings based on a few mechanical and geometrical characteristics of the buildings that are used to derive the bilinear capacity spectrum of the ESDOF model [96], [97]. The capacity spectrum method has been applied considering the formulation of the N2 procedure. This method focuses on the effects of the uncertainties related to the mechanical properties and limit states, showing the role of each uncertainty on the results. In order to derive the capacity curve, a URM building of height H is schematized with a stick model based on [98] where each floor is represented with a lamped mass. The capacity curves have been extracted considering the effects of uncertainties related to the specific weight of masonry, shear modulus, shear strength, resistant wall areas, floor loading, inter-story height, and the non-uniform response of the masonry panels [97]. In particular, the authors use Taylor’s series around the mean value to account for the uncertainties of the parameter. The propagation of uncertainties has been studied considering the influence of each parameter at a time on the capacity curve. The results show that the most relevant parameters are the resistant wall area in the considered direction and the shear strength. Four random limit states that lie on the mean point have been analyzed as a function of buildings parameters. Then, the fragility curves are derived, including all uncertainties’ effects.
The damage thresholds’ types and the corresponding values for each presented CSB method have been shown in Table 2 and compared with the limit states proposed in HAZUS [99], Eurocode 8-part 3 [81], and FEMA 356 [100]. The damage thresholds can significantly influence the fragility curve shape, but the values proposed by various authors and codes can be very different, as shown in Table 2, where the damage thresholds are defined as a function of the inter-story drift ratio IDR, the roof displacement, and the spectral displacement.
Table 2. Damage thresholds definition with corresponding values of the codes and the mentioned CSB methods.
| Method name | Method type | Damage threshold type | Limit states and their values | |||
|---|---|---|---|---|---|---|
| HAZUS (pre-code) | Code | IDR (%) | Slight damage | Moderate damage | Extensive damage | Complete damage |
| 0.2 | 0.5 | 1.2 | 2.8 | |||
| HAZUS (low-code) | 0.3 | 0.6 | 1.5 | 3.5 | ||
| Eurocode 8-Part 3 | Code | Roof (top) displacement | Limited damage | Significant damage | Near collapse | |
| Yielding point of the idealized bilinear capacity curve | 75% of the top displacement capacity corresponding the total base shear | Corresponding displacement of 80% of peak base shear | ||||
| FEMA 356 | Code | IDR (%) | Immediate occupancy | Life safety | Collapse prevention | |
| 0.3 | 0.6 | 1 | ||||
| FaMIVE (in-plane) | CSB | IDR (%) | Damage limitation | Significant damage | Near collapse | collapse |
| 0.18–0.23 | 0.65–0.9 | 1.23–1.92 | 1–2.8 | |||
| FaMIVE (out-of-plane) | 0.33 | 0.88 | 2.3 | 4.8 | ||
| Mechanical method (RISK-UE project) | CSB | Spectral top displacement | Slight damage | Moderate damage | Extensive damage | Complete damage |
| 0.7 dy | dy | dy + 0.25(du – dy) | du | |||
| Pagini et al. | CSB | Spectral top displacement | 0.7 dy | 1.5 dy | 0. 5 (du + dy) | du |
Table 3. Details about each CSB method and the relevant references for the applications.
| Method | Data collection | Collapse type | Output | Brief description | References |
|---|---|---|---|---|---|
| FaMIVE | On-site survey | In-plane and out-of-plane | Collapse acceleration, the most probable collapse mechanism capacity curve, performance point, fragility curve | Collapse multipliers have been calculated for nine predefined collapse mechanisms, and the most probable mechanism has been derived. Fragility curves can be derived directly from the collapse multipliers or using the CSB procedure. | [32], [90], [102], [103], [104] |
| Mechanical method (RISK-UE Project) | Exposure Database and on-site survey | In-plane | Capacity curve, performance points, fragility curve | Derivation of bilinear capacity curves for building typologies based on structural description and using CSB procedure to derive the performance points. | [95], [1], [105], [106] |
| Pagini et al. | Exposure Database and on-site survey | In-plane | Capacity curve, performance points, fragility curve | Derivation of bilinear capacity curves considering uncertainty effects based on the structural description and using CSB procedure to derive the performance point. | [96], [107] |
CSB methods cannot precisely reflect certain dynamic phenomena such as near-field velocity pulses that can considerably influence the structural responses [101]. Table 3 summarizes each aforementioned CSB methods' main feature comparing the type of data collection required to define the input data, the collapse mechanisms considered in the methods, and the relevant references for some case studies. Note that the input demand data is considered nonlinear response spectra with different return periods. The data collection type can be done by performing on-site surveys to record the structural and geometrical detail of the building samples or exposure database provided by the authorities to define the general data about the building typologies at a large scale. All methods are proposed for URM buildings with different horizontal structures, including the flexible, the semi-rigid, and the rigid floor. Among the analyzed methods, only the FaMIVE procedure [32] considers the out-of-plane collapse mechanism and the collapse multipliers that can be evaluated from the structural analysis. The simplified mechanical method (RISK-UE project) [93] considers only the global mechanism but propose a set of European typological masonry structures and, for each of them, the authors evaluated the capacity curves parameters that are presented in a table so that the user doesn’t need to define a structural model for a large scale vulnerability assessment. The uncertainties have been considered both in FaMIVE and Pagini et al. [96] methods; in particular, the last method proposed a sensitivity analysis of the results as a function of each parameter. All the CSB methods are suitable to consider the record-to-record variability in terms of using seismic records as demands.
3.1. Software packages
The main concept of these methods is the intersection of the capacity curves and the seismic demands to derive the performance points in different damage thresholds [16], [108]. Some software packages are related to a specific region, and the capacity curves are related to a typical structural system and configuration in that specific area. Moreover, their exposure can be at urban or multi-level scale, meaning country scale. Geographical Information Systems (GISs) and remote sensing technologies have helped create comprehensive databases and systems for data exposure, analysis, and damage evaluation [109]. All the information about the CSB software packages can be found in Table 4, including relevant references for more information.