High-fidelity simulations in complex geometries: Towards better flow understanding and development of turbulence models

1. Numerical simulations of turbulent flows

Simulations of turbulent flows constitute an excellent complement to wind-tunnel testing. Whereas the latter enables flexibility in terms of operating conditions and Reynolds number, the former provides highly detailed characterizations of the flow case under study. Moreover, simulations allow to artificially manipulate the flow conditions in order to test hypotheses and isolate certain phenomena of interest. Some examples of these numerical experiments are the concept of minimal flow unit [1] (which allows to isolate the near-wall cycle of turbulence in narrow computational boxes), the assessment of the role of the wall by studying homogeneous shear turbulence [2] and the analysis of optimal fluxes of Reynolds stresses [3]. In any case, a complementary and synergistic approach to study wall-bounded turbulence [[4], [5], [6]], including both simulations and experiments, enables to benefit from the advantages of the various techniques.

One of the first reported simulations are the weather predictions by Richardson [7] in 1922, where he proposed a method based on using thousands of “human computers”; note that his approach required weeks to complete few hours of weather prediction. Some other early simulations are the ones of low-Reynolds-number flow around a cylinder by Thom [8] and Kawaguti [9], as well as the vortex street after a plate by Fromm and Harlow [10]. In 1947, Kopal [11] compiled a number of tables defining the hypersonic flow around yawing cones, where the results were obtained numerically at the Massachusetts Institute of Technology (MIT). Two decades later, in 1968, Chorin [12] proposed his pressure-projection method for the solution of the Navier–Stokes equations. The first large-eddy simulation (LES), in which the largest scales are resolved and only the smallest ones are modeled, was conducted for a turbulent channel flow by Deardorff [13] in 1970, using a total of 6, 720 grid points and the Smagorinsky model [14]. In 1987, Kim et al. [15] performed a direct numerical simulation (DNS) of a turbulent channel at a friction Reynolds number Reτ = huτ/ν = 180 (where h is the channel half-height, uτ the friction velocity and ν the fluid kinematic viscosity). In DNS all the relevant flow scales are resolved, and the study by Kim et al. [15] employed around 4 million grid points to discretize the domain. This seminal study is considered the starting point of the numerical simulation research in wall-bounded turbulence. The difficulties of the most commonly used modelling approaches to capture essential aspects of turbulent flows, as discussed in §3.1, motivate the use of high-fidelity simulation approaches such as DNS in order to shed light into their physics.

After the first channel-flow simulation by Kim et al. [15], Moser et al. [16] increased the Re range by performing channel DNSs at Reτ = 395 and 590; later, del Álamo et al. [17] simulated channel flows at Reτ = 950 and 1, 900 (although the latter was in a small computational box). A DNS of turbulent channel flow at Reτ = 2, 003 in a large computational box was then carried out by Hoyas and Jiménez [18], who replaced the original wall-normal discretization based on Chebyshev polynomials in Kim et al. [15] by a more efficient compact-finite-difference discretization [19]. Recent channel-flow simulations at higher Re include the DNS at Reτ = 4, 200 by Lozano-Durán and Jiménez [20], at Reτ = 5, 200 by Lee and Moser [21] and at Reτ = 8, 000 by Yamamoto and Tsuji [22].

While the turbulent channel flow is pressure driven, there is another simple flow relevant to the study of wall-bounded turbulence, i.e. the Couette flow, where the shear is introduced through wall velocity. Some relevant simulations of this flow case are those by Avsarkisov et al. [23], Pirozzoli et al. [24] and Lee and Moser [25]. The turbulent channel and Couette flows are the simplest wall-bounded turbulent flows when it comes to geometry, since the flow is statistically two-dimensional and fully-developed. This geometrical simplicity allows to very efficiently simulate the flow, but the cases of industrial relevance are significantly more complex. One step in the direction of increased geometrical complexity is to consider a spatially-developing turbulent boundary layer (TBL), in which the flow is non-homogeneous in the streamwise and wall-normal directions x and y. The slow spatial development in zero-pressure-gradient (ZPG) TBLs was accounted for in different ways in various studies in the literature: Spalart [26] considered a periodic flow in x, and used a multiple-scale approach to model the TBL growth. Following this method, he performed DNS at a Reynolds number based on momentum thickness Reθ = 1, 410. Schlatter and Örlü [27] also considered a periodic flow in x, and introduced a fringe region to ensure that the outflow would match the laminar inflow conditions, given by a Blasius profile (which is then tripped to produce the transition to turbulence [28]). They performed DNS up to Reθ = 4, 300 and well-resolved LESs up to Reθ = 8, 300 [29]. An alternative approach was considered by Sillero et al. [30], who used an auxiliary simulation to produce the inflow conditions, and a convective boundary condition at the outflow. Doing so, they performed DNS of ZPG TBL up to Reθ = 6, 600.

As mentioned above, flows of industrial relevance involve more complex geometries. In the present chapter we discuss cases in slightly more complex scenarios, which are still far from those present in industrial flows, but exhibit additional features beyond those of canonical wall-bounded turbulence. The discussed simulations are based on the spectral-element method implemented in the code Nek5000 [31], as discussed in §2. The cases under consideration are presented in §3: we discuss turbulent flows through ducts, see §3.1; in §3.2 we discuss the flow around a wall-mounted obstacle; pressure-gradient TBLs around wing sections are discussed in §3.3; and turbulent flows through straight and bent pipes are presented in §3.4. Finally, a summary of this review can be found in §4.

2. The spectral-element method

The simulations discussed in §3 were carried out with the spectral-element code Nek5000 [31]. The spectral-element method (SEM) was initially proposed by Patera [32], and in this method the Navier–Stokes equations are cast into weak form, with the Galerkin approximation being used for spatial discretization. In the cases under consideration here, we use the $P_{N} - P_{N - 2}$ formulation by Maday and Patera [33], which implies that the pressure space is of two orders lower than that of the velocity (therefore one has N − 2 points per element for the pressure). The SEM implementation in Nek5000 [34] involves hexahedral spectral elements, where C0 is imposed across element boundaries, and the spatial discretization is based on Lagrange interpolations of Legendre polynomials. Note that the quadrature points inside spectral elements follow the Gauss–Loboatto–Legendre (GLL) distribution, and that as discussed by Fischer [35] very efficient matrix-matrix multiplications are possible due to the tensor-product structure. Regarding the time integration, an explicit treatment through third-order extrapolation (EXT3) is considered for the convective terms, and the viscous terms are solved implicitly through third-order backward differentiation (BDF3). The resulting system is solved by a pressure-correction method (see Offermans et al. [36] for additional details), where the velocity is solved by means of conjugate gradients using Jacobi preconditioning, and the pressure is solved through the generalized minimal residual method (GMRES). The pressure is first projected on a subspace of previous solutions [37], an operation that significantly reduces the required pressure iterations for convergence. Then, a pressure preconditioner is constructed based on the additive overlapping Schwarz method [35], which requires efficient coarse-grid solvers. The coarse-grid solve, which is difficult to parallelize, can be performed in two different ways: through a Cholesky matrix factorization, i.e. the so-called XXT method [38]; and through a V-cycle algebraic multi-grid (AMG) solver [39]. In general, the former exhibits better performance in smaller problems, whereas the latter is preferred in very large simulations. Nek5000 is written in Fortran77/C, and a message-passing interface (MPI) is used for the parallelization.

More challenging simulations are progressively being enabled in Nek5000 through more advanced automatic-meshing techniques. In particular, we consider adaptive mesh refinement (AMR), which relies on an error indicator to refine the mesh dynamically using non-conformal elements [40]. In Fig. 1 we illustrate an example of mesh obtained with AMR for the flow around a NACA4412 wing section [41], where the refinement is automatic and uniquely based on an error threshold [42]. This advanced meshing and simulation approach will allow to accurately simulate progressively more complex geometries at higher Reynolds numbers.

3. Direct numerical and large-eddy simulations in complex geometries

3.1. Turbulent flow through ducts

The turbulent flow through a square/rectangular duct is slightly more complex than that in plane channel flows due to the presence of the side walls, as shown in Fig. 2. In the particular case of straight, fully-developed ducts, the interactions among bursting events on the horizontal and vertical walls, close to the corners, produce the so-called secondary flow of Prandtl's second kind [43]. The secondary flow lies on the cross-stream yz plane, and consists of four pairs of counter-rotating vortices with the flow directed towards the corner as shown in Fig. 3. Note that this type of secondary flow is entirely due to turbulence, and it is therefore absent in laminar ducts. It is however possible to introduce secondary flows in laminar flows by manipulating the streamwise vorticity field, for instance through wall oscillations, as in the study by Straub et al. [44]. Moreover, there is another type of secondary flow which is present in curved or developing flows. This is the so-called Prandtl's secondary flow of first kind [43], and it is present for instance in bent pipes [45,46]. The secondary flow of Prandtl's first kind is also present in laminar flows.

Although the secondary flow of Prandtl's second kind only amounts to around 2–3 % of the bulk velocity [48], it may significantly change the flow topology and integral quantities, especially in ducts with low aspect ratio AR (which is defined as the ratio between the duct total width Wd and its total height H). The turbulent flow through a square duct was first studied through DNS by Gavrilakis [49] and by Huser and Biringen [48], both in the early 1990s. The study by Gavrilakis [49], at an average friction Reynolds number of ${\bar{R e}}_{τ} = 150$ (based on the friction velocity averaged over the whole perimeter), revealed that each of the streamwise vortices is associated to two mean streamwise vorticity cells of opposite signs. The DNS by Huser and Biringen [48] at ${\bar{R e}}_{τ} = 300$ showed that the secondary flow was essentially due to the non-homogeneous interactions of near-wall events on horizontal and vertical walls, and the corresponding transfer of momentum between the cross-stream velocity components. This notion has been recently explored in square ducts by Vidal et al. [50], who analyzed cases with straight and rounded corners, and used the concept of local preferential direction (LPD) of the bursting events to quantify the local tilting of the flow, an analysis in agreement with the conclusions by Huser and Biringen [48]. This was further supported by analyzing rectangular ducts with straight and curved corners [51], and the use of quadrant analysis [52] identified the role of the various Q events near the wall in the formation of the secondary flow. External corners [53] and wavy walls [54] also produce non-homogeneous interactions of the near-wall events, and therefore lead to the formation of secondary flows as well.

Vinuesa et al. [55] used the spectral-element code Nek5000 [31] to perform DNSs of the turbulent flow through ducts with AR varying from 1 to 7 at Reτ,c ≃ 180 (which is the friction Reynolds number based on centerplane friction velocity), and with AR = 1 at Reτ,c ≃ 330. An instantaneous visualization of the flow field in one of the cases is shown in Fig. 4, where the interactions among bursting events close to the corners are noticeable. In addition to the role of Prandtl's secondary flow of second kind, Vinuesa et al. [55] reported the contribution of another in-plane effect, namely the growth of the side-wall boundary layers. Whereas the secondary flow lifts the near-wall flow at the duct centerplane, the side-wall boundary layers accelerate the duct core; therefore the former reduces the centerplane wall-shear stress and the latter increases it, as illustrated in Fig. 2. This results in a non-monotonic trend with AR of the inner-scaled centerline velocity $U_{c}^{+} = U_{c} / u_{τ}$ , which decreases going from AR = 1 to 3, and increases again starting at AR = 5. This is due to the fact that, for AR = 3, the effect of the side-wall boundary layers, i.e. increase of centerplane friction, dominates over that of the secondary flow. For wider ducts the former effect is reduced, and the centerplane wall-shear stress is reduced due to the vertical convection of near-wall flow induced by the secondary vortices.

DNS of turbulent square ducts was also conducted by Pinelli et al. [56] up to ${\bar{R e}}_{τ} = 300$ . They emphasized the connection of the near-wall streaks with the spanwise wall-shear stress curve, and how its local extrema are associated with preferential locations of high- and low-speed streaks. As opposed to spanwise-periodic channels [57], turbulent ducts exhibit a non-uniform wall-shear stress curve τw(z), a fact that indicates that the duct geometry influences the location of the streaks, at least close to the corner. In square ducts the first streak in the spanwise direction is preferentially located at a distance $z_{c}^{+} ≃ 50$ [56], where zc is the spanwise distance measured from the corner, and the superscript ‘+’ denotes scaling with the viscous length ℓ* = ν/uτ,c, where uτ,c is the centerplane friction velocity. This distance is reduced to $z_{c}^{+} ≃ 38$ in the hexagonal ducts [58] due to their larger vertex angle, which modifies the interactions of near-wall events from the horizontal and inclined walls. An additional important aspect of turbulent ducts is the fact that the limited spanwise width determines the number of near-wall streaks that can exist on the wall, keeping in mind that the spanwise distance between two streaks of opposite signs is approximately 50 viscous units [59,60]. Based on this, Uhlmann et al. [61] defined the concept of marginal turbulence, a state just above the minimum Reynolds number for sustained turbulence. When the friction Reynolds number is below ${\bar{R e}}_{τ} ≃ 80$ , the inner-scaled width in a square duct is below 160 viscous units, which is the width required to fit three near-wall streaks. In this marginally-turbulent state, the secondary flow consists of four vortices, and only after performing very long time averages the eight-vortex pattern is recovered. Another important aspect of the τw(z) curve is its behavior at very high Reynolds numbers: in principle, except very close to the corners, for large enough values of $W_{d}^{+}$ the wall-shear stress curve should be essentially flat due to the uniform distribution of near-wall streaks in z. This has been reported to be the case when the overlap region is represented by a logarithmic law [62].

Four additional DNSs have been recently performed by Vinuesa et al. [47], with AR = 10 and 14.4 at Reτ,c ≃ 180, and with AR = 1 and 3 at Reτ,c ≃ 360. In order to characterize the secondary flow, they used the in-plane mean kinetic energy $K = 1 / 2 (V^{2} + W^{2})$ , where V and W are the mean wall-normal and spanwise velocities. Their conclusions reflect the need of aspect ratios of at least 10 in order to obtain conditions at the duct core similar to those in spanwise-periodic channels. This has important implications in experimental studies [63], and a similar minimum value of AR was reported in the experiment by Rhodes and Knight [64]. Some additional difficulties are present in channel-flow experiments, mainly involving flow development and inflow conditions [[65], [66], [67], [68]].

The difficulties of predicting the secondary flow of Prandtl's second kind using Reynolds-averaged Navier–Stokes (RANS) simulations, in particular based on a linear constitutive relation between the Reynolds stresses and the mean flow, were discussed by Spalart [69]. For instance, differences even in the mean velocity profile were observed between the RANS of turbulent hexagonal ducts by Turgut and Sari [70] and the DNS by Marin et al. [58]. In this context, the use of high-quality databases from DNS to develop improved RANS models, based on evolutionary algorithms, has been documented by Weatheritt and Sandberg [71]. An important indicator of the quality of the data is the convergence of turbulence statistics, as thoroughly studied by Vinuesa et al. [72], both in channel and in duct flows. Further insight into the mechanisms producing the secondary flow can be obtained by analyzing three-dimensional coherent structures, as in the work by Atzori et al. [73]. Note that although these structures share some similarities with the streamwise vortices found in Couette flows [23], they are fundamentally different. Other interesting databases of turbulent duct flow available in the literature are the DNS by Zhu et al. [74] at a friction Reynolds number of 300, the numerical simulations up to ${\bar{R e}}_{τ} = 600$ by Zhang et al. [75] and Raisei et al. [76] and the DNS up to a numerically high ${\bar{R e}}_{τ}$ of 1000 by Pirozzoli et al. [77]. Finally, Samanta et al. [78] performed a DNS of the turbulent flow through a square duct over a porous bed. In their study, the porous bed is modeled through the volume-averaged Navier–Stokes (VANS) equations [79,80]. Samanta et al. [78] reported an increase in the magnitude of the secondary flow of a factor of 4 compared with the case with solid walls, a fact that highlights the relevance of the near-wall structures in the formation of the secondary flow. An instantaneous visualization of the flow through the porous duct is shown in Fig. 5 (top). This connection was also reported by Pinelli et al. [56] and Vinuesa et al. [72] in the context of square and rectangular ducts, since the probability density function (pdf) of the position of the near-wall streaks is in very good agreement with the streamwise vorticity field. This is illustrated in Fig. 5 (bottom).

3.2. Wall-mounted obstacles

A geometrically more complex case is the flow around a wall-mounted obstacle, due to the inherent three-dimensionality of the mean flow and the complex multi-scale character of the wake. In 2012, the CFD Society of Canada organized a Challenge, where different researchers worldwide would use various numerical approaches to simulate the flow around a wall-mounted square cylinder of aspect ratio 4, placed on a ZPG TBL. The reference data was extracted from the particle-image velocimetry (PIV) measurements by Bourgeois et al. [81], where the Reynolds number based on cylinder side d and freestream velocity U∞ was Red = 11, 000. In these conditions, the ZPG TBL had a 99 % boundary-layer thickness δ99 = 0.72d at the obstacle location, and the Reynolds number based on momentum thickness was Reθ ≃ 1, 000. Some of the most relevant studies presented during the Challenge were the LESs by Shademan et al. [82] and Chen et al. [83], and the DNS by Saeedi et al. [84]. Due to the complexity of the flow case, an accurate simulation strategy will require the geometrical flexibility of the spectral-element method. On the other hand, since the obstacle is placed on a canonical ZPG TBL at Reθ ≃ 1, 000, it is possible to use an auxiliary simulation to more efficiently produce the ZPG inflow conditions, and use those to drive the main wall-mounted obstacle simulation. This approach was adopted by Vinuesa et al. [6], who used the Fourier–Chebyshev code SIMSON [85] to efficiently simulate the simple ZPG case, and Nek5000 [31] to perform a DNS of the flow around the wall-mounted square cylinder, using the ZPG as inflow conditions. The coupling of the two codes is discussed in detail in Ref. [6].

The complexity of the flow field in the simulation by Vinuesa et al. [6] can be observed in Fig. 6. Some of the most prominent elements in the field are the separated region upstream of the obstacle, the turbulent flow around the sides of the wall-mounted cylinder, and the massively separated wake. Note that in this case the separation is induced by the geometry, due to the sharp edges on the sides of the square section. A very important aspect of this flow is the effect of the inflow conditions, i.e., whether the state of the incoming boundary layer affects the characteristics of the wake. Interestingly, in the 2012 Challenge a majority of the research groups reported the correct wake Strouhal number of St = 0.1 ± 0.03 measured by Bourgeois et al. [81]. However, the flow statistics differed significantly among groups, a fact that indicates that the geometry plays a major role in the separation (and therefore in the structure of the wake). This motivated an additional simulation with a laminar inflow, adjusted such that the value of Reθ would also be 1, 000 at the obstacle location [6]. This simulation also produced a value of St ≃ 0.1, and the features of the wake right downstream of the cylinder did not significantly differ from those in the turbulent-inflow case. The separation is induced by the geometry, as well as the wake shedding frequency. Therefore, it is not necessary to perform a high-fidelity simulation in order to obtain a good estimation of St. On the other hand, the wakes in the turbulent- and laminar-inflow cases differ farther downstream. The work by Vinuesa et al. [6] shows that the mean velocity in the wake of the experimental measurements is in better agreement with that of the laminar-inflow simulation. This suggests that perhaps the tripping and/or the development length in the experiment might have been insufficient [81] for a fully-turbulent ZPG TBL to develop at the obstacle location.

Another interesting phenomenon present in this flow is the interaction between the incoming flow and the vortex around the obstacle. This interaction has been studied numerically by Diaz-Daniel et al. [88] in a cubic obstacle, and experimentally by Monnier et al. [89,90] and Nagib and Corke [91] in arrays of obstacles emulating urban environments. The numerical results by Vinuesa et al. [6] show that the laminar-inflow case exhibits a prominent vortex around the obstacle, visible even in the instantaneous field. This is however not observed in the turbulent-inflow instantaneous field, and only becomes visible when performing the time average. This is connected to the fact that the incoming turbulence in this case is modulated by the recirculation induced by the obstacle, therefore producing a fluctuating behavior in the vortex. The vortex in the time-averaged field from the turbulent-inflow simulation is smaller than that in the laminar case, a fact connected to the respective sizes of the recirculation regions. The complex flow around wall-mounted obstacles has important implications in the context of climate simulations [87], and also urban environments [92,93], as shown in Fig. 7. This figure shows a high-fidelity simulation of the turbulent flow in a simplified urban environment, similar to those considered for instance in the experiments by Monnier et al. [89,90].

3.3. Turbulent boundary layers around wing sections

Despite the relevance of analyzing turbulent flows in simple geometries, such as the ZPG TBL [4,27,30,94], in practical applications the boundary layer is subjected to streamwise pressure gradients. If the TBL is subjected to an adverse pressure gradient (APG) then it is decelerated, and if it is exposed to a favorable pressure gradient (FPG) it is accelerated [95,96]. These effects have important implications when it comes to the flow structure [97,98] and the impact of the streamwise flow history on the local features of turbulence [99,100]. A widely used parameter to characterize the PG magnitude is the so-called Clauser pressure-gradient parameter [101,102], which is defined as β = δ*/τwdPe/dx (where δ* is the displacement thickness and dPe/dx is the streamwise pressure gradient). One way in which a streamwise PG can be induced on a TBL is through surface curvature: the geometry of an airfoil is such that an APG is produced on its suction side, and a mild FPG on its pressure side. Therefore, it is important to understand the effect of the pressure-gradient magnitude, and in particular of the β(x) evolution, on the features of TBLs.

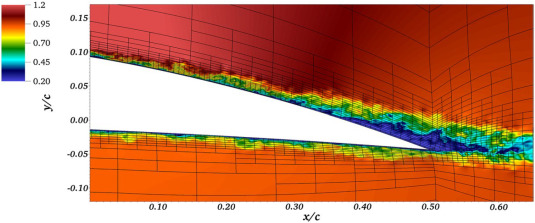
One of the first structure-resolving simulations of the flow around wings was performed in 1996 by Jansen [103], who carried out an LES of the flow around a NACA4412 wing section at Rec = 1.64 × 106 (where Rec is based on U∞ and the chord length c). In addition to the problems associated to the limited computational resources available at the time, Jansen [103] reported that a large source of error in the simulations was due to the use of low-order numerical methods and recommended the use of a high-order method for accurate simulations of turbulence. He used several experimental databases as a reference [[104], [105], [106]], and the mentioned limitations did not allow him to obtain very good agreement between numerical and experimental results. Highly resolved direct numerical simulations have been recently conducted by Hosseini et al. [107] and Vinuesa et al. [108], who simulated the turbulent flow around a NACA4412 wing section at Rec = 400, 000 and angle of attack of 5°. The finely resolved features in the flow can be observed in Fig. 8. DNS has also been employed by Hoarau et al. [109] and by Rodríguez et al. [110] to simulate the symmetric NACA0012 airfoil, which exhibits less intense APG conditions. Note that the importance of using high-fidelity simulations to accurately characterize complex cases, including strongly decelerated and separated regions [111], was highlighted in a recent report by NASA [112].

Vinuesa et al. [113] have recently performed four well-resolved large-eddy simulations of the TBLs around a NACA4412 section at Rec values ranging from 100, 000 to 1, 000, 000. The flow fields in these cases are shown in Fig. 9, where the increasing scale separation with Re can be observed. A very important conclusions of their work is the following: despite the fact that both β and Re increase the energy of the large-scale motions in the outer region of TBLs, their respective mechanisms are different. In particular, the effect of APGs is stronger at lower Reynolds numbers [114], a fact that is reflected in the wall-normal mean velocity distribution [115]. This is due to the fact that the large-scale motions associated to APGs, induced by an enhanced wall-normal convection, are larger in y and are more inclined with respect to the horizontal direction [97] than typical large-scale motions in ZPGs. Therefore, an adequate knowledge of the energizing mechanisms of the large scales, and the contributions from increase in Reynolds number and from higher APGs, may help to reproduce some of the most relevant features in turbulent wings. The same approach was adopted by Tanarro et al. [116] to simulate the turbulent flow around a NACA0012 wing section at Rec = 400, 000. They further characterized the differences in large-scale motions produced by increase in Reynolds number and in APG magnitude. Note that several other recent studies have used LES to characterize the flow around symmetric airfoils [[117], [118], [119], [120]]. The author is currently working on simulating more complex geometries, such as the flow around finite wings, to assess the impact of the wing-tip vortices on the aerodynamic performance of the wing. An example of this type of simulation is shown in Fig. 10, where a finite wing with a blunt wing tip at a low Rec = 1, 000 is shown. Note that the region of negative streamwise vorticity observed here is associated to the roll-up from the pressure to the suction sides of the wing, i.e. from high to low pressure.

Finally, another interesting application of the effect of β(x) on TBLs lies in the possibility of predicting the skin-friction curve of a certain APG TBL. Note that the widely studied ZPG TBL is a case subjected to a constant value of β = 0 (see e.g. the numerical work by Simens et al. [121]), and that as reported by Bobke et al. [99] it is possible to define constant-β APG cases which essentially constitute well-behaved [122] representations of a certain APG TBL of some β magnitude. These notions were extended experimentally by Sanmiguel Vila et al. [123,124]. By analyzing APG TBLs with various β(x) curves, it can be observed [125] that the APG skin-friction curve Cf,APG can be obtained empirically in terms of the ZPG skin-friction coefficient Cf,ZPG and shape factor HZPG (note that the shape factor is the ratio of the displacement and momentum thicknesses, H = δ*/θ) as follows: $C_{f, A P G} = \frac{C_{f, Z P G}}{H_{Z P G}^{\bar{β} / 2}} .$ Since there a number of empirical correlations for Cf and H in ZPG TBLs (see for instance Refs. [126,127]), it is in principle possible to obtain the skin-friction curve of any APG TBL using equation (1), given its β(x) curve. The averaged APG magnitude $\bar{β}$ is defined as: $\bar{β} (R e_{θ}) = \frac{1}{R e_{θ} - R e_{θ, 0}} \int_{R e_{θ, 0}}^{R e_{θ}} β (R e_{θ}) d R e_{θ},$ where Reθ,0 is the Reynolds number based on momentum thickness where averaging is started, which in the work by Vinuesa et al. [125] is around 1, 000. An excellent agreement between the predictions of Cf obtained from equation (1) and reference data can be observed in Fig. 11.

3.4. Turbulent flow through straight and bent pipes

The fully-developed turbulent flow through a straight pipe is an excellent test case to study canonical high-Reynolds-number wall-bounded turbulence, due to the azimuthal symmetry of the pipe, and the lack of secondary flows that may affect the local properties of turbulence [5,67]. Turbulent pipe flow measurements carried out by the Princeton Superpipe group [128,129], using pressurized air to manipulate the fluid viscosity, have reached unprecedented values of Reτ up to around 500, 000. However, possible inaccuracies in the near-wall measurements due to the extreme reduction of the viscous length ℓ* [130,131] have motivated the development of a new high-Re pipe flow facility, the so-called CICLoPE [132], where the maximum Reτ is around 60, 000 but the range of ℓ* allows accurate near-wall measurements [133]. Despite its relative geometrical simplicity, turbulent pipe flows have not been as extensively simulated as channel flows among other reasons due to the problems arising from the singularity present at the pipe center when using cylindrical coordinates (as discussed for instance in Ref. [134]). The first sufficiently resolved DNS of turbulent pipe flow was performed by Eggels et al. [135] at Reτ = 180, using a streamwise length of 10R (where R is the pipe radius), which might be insufficient to capture the contributions of the most energetic turbulent structures (a minimum pipe length of 25R was reported by Chin et al. [136]). More recently, Wu and Moin [137] performed a DNS of pipe flow at Reτ = 1, 142 using a second-order finite-difference code. The spectral-element code Nek5000 [31] was used by El Khoury et al. [138] to conduct DNSs of pipe flow from Reτ = 180 up to 1, 000, with a streamwise length of 25R. Their study focused on the Reynolds-number effects on turbulence statistics, and they reported differences in the pressure fluctuations among pipes, channels and ZPG TBLs. Other recent pipe DNSs include the studies by Boersma [139], Wu et al. [140] and Ahn et al. [141], the latter at Reτ = 3, 008. Wall modelling in turbulent pipe flows was discussed by Ferrer et al. [142] in the context of spectral elements. Furthermore, a DNS of the flow through a complex pipe, denoted as the Food and Drug Administration (FDA) nozzle (which has important implications in biomedical applications) was simulated by Sánchez Abad et al. [143] using Nek5000, and the flow can be observed in Fig. 12. These results exhibit the high sensitivity of this flow case, and the need for high-order numerical simulations in biomedical applications.