A review of meta-heuristic algorithms for reactive power planning problem

1. Introduction

Nowadays, reactive power planning (RPP) problem has become one of the most challenging problems in power systems. It has been an important stage of transmission expansion planning (TEP) problem in recent years [1], [2], [3]. In addition, reactive power control/dispatch is an important function in the planning process for the future of power systems. It aims to utilize all the reactive power sources efficiently, which are suitably located and sized in the planning process [4], [5], [6], [7], [8], [9], [10].

Generally, the various RPP solutions are divided into three groups which are analytical approaches [11], [12], [13], arithmetic programming approaches [3], [4], [11], [12], [13], [14], [15], [16], [17], [18], [19], [20], [21], [22], [23], and meta-heuristic optimization techniques. Various Meta-heuristic Optimization Algorithms (MOA) have been applied to the RPP problem such as Genetic Algorithms (GA) [5], [24], [25], [26], [27], [28], [29], [30], [31], [32], [33], Differential Evolution (DE) [6], [17], [24], [34], [35], [36], [37], [38], [39], [40], [41], [42], Harmony Search (HS) [43], [44], [45], Seeker Optimization Algorithm (SOA) [46], [47], [48], Evolutionary Programming (EP) [49], [50], [51], [52], [53], [54], Ant Colony Optimization (ACO) [7], [55], Immune Algorithm (IA) [8], Particle Swarm Optimization (PSO) [2], [9], [16], [56], [57], [58], Artificial Bee Colony (ABC) [59], Gravitational Search Algorithm (GSA) [60], [61], Firefly Algorithm (FA) [62], Teaching Learning Algorithm (TLA) [63], Chemical Reaction Optimization (CRO) [64], Water Cycle Algorithm (WCA) [65], and Differential Search Algorithm (DSA) [66]. Hybrid techniques have been suggested in some researches that make use of advantages of different algorithms simultaneously to improve the quality of solution [5], [10], [16], [53], [55], [67], [68], [69], [70], [71], [72], [73], [74], [75].

Also, multi-objective formulation of optimization problems for reactive power planning and operation has been treated using the mathematical sum approach [1], [11], [24], [25], [28], [35], [36], [37], [38], [50], [51], [53], [56], [68], weighting functions [27], [29], [40], [43], [44], [47], [69], ε-constraint approach [6], [18], [20], [43], [76], [77], fuzzy goal programming techniques [28], [58], and Pareto concept [4], [8], [16], [17], [26], [31], [32], [33], [34], [57].

Various conventional methods have been presented to solve the RPP problem and assured their incompetence in handling multi-objective nonlinear problems and they may converge to a local optimum. MOAs that mimic the nature opened a new era in computation. For the past decades, numerous research applications of MOAs have been concentrated for solving the RPP problem. In this particular area, the research is still young which broadens the scope and viability of MOAs exploring new modifications and developments in solving the RPP problem. This paper presents a broad overview of solution methods for solving the RPP problem which are analytical approaches, arithmetic programming approaches, and meta-heuristic optimization techniques. Also, the different applications of meta-heuristic algorithms for solving the RPP problem are extensively reviewed and thoroughly discussed. Furthermore, the multi-objective formulations of reactive power planning and operations are studied to clarify their merits and demerits. This paper is organized as follows. The formulation of the RPP problem is presented in Section 2. Section 3 discusses the different methods applied to solve the RPP problem. The multi-objective formulations of the RPP problem are discussed in Section 4. The concluding remarks are highlighted in Section 5.

2. General formulation of the RPP problem

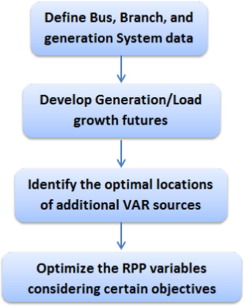
The purpose of the RPP problem is to determine “where” and “how many” new VAR compensators must be added to a network for a predefined horizon of planning at minimum cost while satisfying an adequate voltage profile during normal conditions and contingencies. Fig. 1 illustrates the flowchart of the RPP problem.

After defining the system data, the generation/load patterns are developed for a predefined horizon of planning. Then, the optimal locations of new reactive power sources are identified. They may be selected according to certain indices or all load buses may be considered as candidate buses [14], [15].

After that, the control variables (RPP variables) are optimized to achieve certain objective functions subject to set of equality and inequality constraints. Control variables include generator bus terminal voltages, reactive power generation of existing and new VAR sources and transformer tap ratio. The generator bus voltages are continuous in nature, while both reactive power generation of existing and new VAR sources and transformer tap ratio are discrete. The dependent variables include load bus voltage magnitude, active power generation at slack bus, the power flows through the transmission lines, and reactive power outputs of the generators.

There are various objective functions that have been utilized in the RPP problem such as minimization of VAR investment cost and system operational cost of real power losses, improvement of voltage profile, and enhancement of voltage stability. However, the modeling of each objective has different shapes. Conventionally, the classical objective of the RPP problem is to achieve the minimum investment cost of additional reactive power supplies and minimize the system operational cost of power losses [1], [11], [24], [25], [28], [35], [36], [37], [38], [50], [51], [53], [56], [68] as follows:(1) $Min F = Min (I_{C} + O_{C})$ where IC is the investment cost of new reactive power supplies and OC is the operational cost of power losses. The investment costs of VAR sources can be generally modeled with two components, a fixed installation cost at bus i (ei) and a variable purchase cost of capacitive or inductive source at bus i (Cci|Qci|), [16], [24], [25], [26], [28], [31], [34], [35], [37], [38], [50], [51], [53], [56], [68] as follows:(2) $I_{C} = \sum_{i = 1}^{N_{c}} (e_{i} + C_{c_{i}} | Q_{c_{i}} |)$ where Nc is the reactive compensator buses. This model requires considering the reactive power devices to be already installed before the optimization for its size. On the other hand, another general model of IC has been used as [1], [2], [3], [27], [43]:(3) $I_{C} = \sum_{i = 1}^{N_{b}} (e_{i} + C_{c_{i}} | Q_{c_{i}} |) β_{C}$ where Nb is the total number of busses, and βC is the binary decision variables for installing capacitive source. Although the complexity of using binary variables to indicate whether the VAR source will be installed, this model will give a chance to consider all load buses to be candidates to install new reactive power sources. Traditionally, the annual cost of energy losses has been used as a direct measure to the operational costs (OC) [1], [16], [24], [25], [28], [31], [34], [35], [36], [37], [38], [51], [53], [56], [68] as follows:(4) $O_{C} = h \sum_{i = 1}^{N_{L}} d_{L} P_{loss}^{L}$ where h is the per unit energy cost, dL is the duration of load level (h), NL is the number of load level duration, and $P_{loss}^{L}$ s the real power loss during the period of load level L. On the other side, the minimization of network transmission power losses (Ploss) has been sometimes used directly instead of converting it to operational costs in the reactive power operation [4], [29], [32], [39], [40], [41], [46], [47] and planning [20], [43], [44], [52]. Also, the power system has to satisfy equality and inequality constraints corresponding to the load flow model and operational variables as follows:(5) $Q_{g_{i}} - Q_{L_{i}} + Q_{C_{i}}^{n} + Q_{C_{i}} - V_{i} \sum_{j = 1}^{N_{b}} V_{j} (G_{i} \sin θ_{ij} - B_{ij} \cos θ_{ij}) = 0, i = 1, 2, \dots N_{b}$ (6) $P_{g_{i}} - P_{L_{i}} - V_{i} \sum_{j = 1}^{N_{b}} V_{j} (G_{ij} \cos θ_{ij} + B_{ij} \sin θ_{ij}) = 0, i = 1, 2, \dots \dots . N_{b}$ (7) $Q_{g i}^{min} ⩽ Q_{g i} ⩽ Q_{g i}^{max}, i = 1, 2, \dots \dots N_{pv}$ (8) $V_{i}^{min} ⩽ V_{i} ⩽ V_{i}^{max}, i = 1, 2, \dots \dots N_{b}$ (9) $T_{k}^{min} ⩽ T_{k} ⩽ T_{k}^{max}, k = 1, 2, \dots \dots N_{t}$ (10) $|S_{L}^{flow}| ⩽ S_{L}^{max}, L = 1, 2, \dots \dots N_{L}$ (11) $0 ⩽ Q_{C e} ⩽ Q_{C e}^{max}, e = 1, 2, \dots \dots N_{C}$ (12) $0 ⩽ Q_{C j}^{n} ⩽ Q_{C j}^{max (n)} \cdot β_{C j}, j \in candidate buses$ (13) $P_{s}^{min} ⩽ P_{s} ⩽ P_{s}^{max}$ where Vi and Vj are voltages at buses i and j, respectively; θij is phase angle between buses i and j; Gij and Bij are mutual conductance and susceptancebetween buses i and j, respectively; (Pgi − PLi) and (Qgi − QLi) are the net real power injection at bus i, and the net reactive power injection at bus i, respectively; QCi is the capacitive or inductive power of existing VAR source installed at bus i. QCin refers to the capacitive or inductive power of new VAR source installed at bus i. Qgi is the reactive power output of a generator i, and Npv refers to the total number of voltage-controlled buses. Vi is the voltage magnitude of bus i. Tk is the tapping change of a transformer k, and Nt refers to the total number of on-load tap changing transformers. Sflow refers to the apparent power flow, Smax is the maximum MVA rating of the transmission lines and transformers, and NL refers to all transmission lines in the system. QCeis the reactive power output of existing VAR source at bus e, $Q_{C}^{max}$ s its maximum capacity, and NC refers to the total number of existing VAR sources. nrefers to the new installed VAR sources, and βC is always equal 1 for the investment cost of VAR sources modeled in Eq. (3). Ps is the active power generation at the slack bus.

3. Solution methods for the RPP problem

RPP is a nonlinear multi-objective constrained combinatorial optimization problem for large power systems with a lot of uncertainties. Generally, the RPP problem has been solved by analytical approaches, arithmetic programming approaches, and meta-heuristic optimization techniques. Fig. 2 depicts the family and subcategories of the solution algorithms for the RPP problem. As shown, the several applications of meta-heuristic algorithms are subcategorized into evolution based, and swarm intelligence [78]. Added to that, hybridization between different algorithms is taken into consideration to improve the solution quality.

3.1. Analytical approaches

Analytical approaches are very important to understand the different effects and benefits of the location and size of reactive power sources [11], [12], [13]. The issues of RPP have been analyzed with reactive power pricing in [11] where a trade-off between the transmission loss and installation cost of new capacitors has been executed incorporating detailed hourly loading conditions. In [12], three economic benefits with assumption of a constant VAR injection and a fixed location have been analyzed. These benefits include reducing losses, shifting reactive power flow to real power flow, and increasing the transfer capability. The economic benefits have been updated by executing a set of optimal power flow (OPF) runs. Also, the reactive market-based of economic dispatch has been addressed in [13]. However, the benefits to the utilities from the allocation, installation, and operation of VAR compensators have not been discussed. Analytical approaches lend a lot of information and clear vision about the economic and technical benefits under different scenarios. They are quite helpful to design future framework of reactive power management and pricing for different players in the deregulated environment. On the other hand, they are time-consuming and may not be suitable for medium and large-scale power systems. Analytical approaches are as accurate as the model developed. They are based on its corresponding OPF which has been usually solved using nonlinear algorithms such as Modular Incore Nonlinear Optimization System (MINOS) [11], [12], [13] using General Algebraic Modeling Systems (GAMS) procedures [79].

3.2. Arithmetic programming approaches

Arithmetic programming approaches are also called Conventional Optimization Algorithms (COAs). A variety of conventional methods have been widely used to solve the reactive power operation and planning for years [14], [15], [16], [17]. COAs have been developed and implemented to solve the RPP problem. Table 1shows a comparison between various COAs that have been applied to the RPP problem.

Table 1. Comparison among COAs implemented to solve the RPP problem.

Category	Ref.	Remarks	Merits	Demerits
NonLinear Programming (NLP) method Modular Incore Nonlinear Optimization System (MINOS) solver⁎	[11], [12], [13]	• MINOS employs a project Lagrangian algorithm with a linear approximation to the nonlinear constraints. It then uses the reduced-gradient algorithm for solving a linearly constrained sub-problem with a sequence of iterations	• Fast computation performance. It solves quickly a large number of single optimizations which corresponds to different loading and contingency conditions	• It is based on simplifications of sequential linearization • It is highly dependent on choosing the starting point • It finds locally optimal solutions
Mixed Integer NonLinear Programming (MINLP) solver (KNITRO 8 solver)	[19]	• The load uncertainty and different contingencies have been considered in multi-scenarios extracted using a scenario tree reduction methodology. KNITRO implements the interior method where, the nonlinear programming problem is replaced by a series of barrier sub-problems	• Fast computational performance. • Very suitable to handle with both continuous and discrete variables • No need for calculating 1st or 2nd derivatives of the nonlinear objectives or constraints • Iterative approach for computing steps	• It could be trapped in a local optimum and there is no guarantee to find the global optimum even if you run the algorithms for infinite long because the diversity of the solutions is limited • The multi-objective functions have been treated mathematically sum for each scenario in [19] • Neglecting the effect of transformer tap changing on the RPP problem in [3]
Interior Point (IP) method	[3]	• RPP problem has been formulated as a stage of TEP problem • The candidate buses to install VAR sources have been selected based on L-index as a voltage stability index
DIscrete and Continuous OPTimizer (DICOPT) solver⁎	[4], [18]	• DICOPT solves a series of NLP and Mixed Integer Programming (MIP) sub-problems. It is based on outer approximation of the objective function, equality relaxation, and augmented penalty of the inequality constraints and the objective function.	• Suitable for solving the RPP problem as a MINLP problem that involves integer variables and continuous variables • Fast computation performance	• It does not necessarily obtain the global optimum • It is based on linear approximations of nonlinear functions at each iterations and accumulating them due to outer-approximations
Penalty Successive Conic Programming (PSCP) method	[22]	• PSCP method is generally a linear program with an additional nonlinear conic constraints corresponding to multiple state constraints as a penalty function • The PSCP algorithm has been solved by polynomial time primal–dual IP methods to find a common value of the decision variables in each state in a successive manner	• Very fast computational method • This method handled with outage scenarios and different load levels under voltage profile and stability constraints	• The solution of each conic program employs a linearization of the power flow equations at the current operating point • High computational burden due to multiple states VAR planning includes outage scenarios and different load levels
Dual Projected Pseudo Quasi-Newton (DPPQN) method	[20]	• This method considered only power losses as a single objective RPP problem • The investment cost for reactive power sources has been handled as budget constraint	• Fast computational technique • Efficient for solving RPP problems	• It becomes too slow if number of variables is large • It ignored the effect of generator voltages and tap changing transformers considering only the VAR patterns as control variables • Complex and high computational burden due to many levels and load cases
Branch and Bound (B&B) method	[21], [23]	• This method employed a sequence of MIP method where, sensitivities of voltage stability margin and voltage magnitude have been used in this RPP formulation • In B&B, the search continues by creating two new sub-problems, each one is then solved by the same procedure, resulting in a search-tree of sub-problems	• No need for restarting the tree search and only a single tree is required • It is fast • It provides good solutions for large-scale power systems	• The formulation has been approximated to be linear using voltage stability margin sensitivities and voltage magnitude sensitivities • It finds locally optimal solutions

⁎: MINOS solver [11], [12], [13], and DICOPT solver [4], [18] have been formulated in GAMS software [79].

3.3. Meta-heuristic optimization algorithms

Meta-heuristic Optimization Algorithms (MOAs) are extensively used in solving multi-objective optimization problems since they can find multiple optimal solutions in a single run. Different MOAs are applied efficiently to solve the RPP problem. Table 2 shows a comparison between various MOAs that have been applied to the RPP problem.

Table 2. Comparison among MOAs implemented to solve the RPP problem.