Dynamics of large-scale fMRI networks: Deconstruct brain activity to build better models of brain function

Introduction

More than two decades ago, the discovery of functional magnetic resonance imaging (fMRI) initiated a rich field of non-invasive human neuroimaging that contributed significantly to our understanding of the brain in health and disorder [1]. Technological advances in MRI scanning have enabled modern fMRI to reach whole-brain coverage at millimeter spatial resolution and sub-second temporal resolution. In addition, fMRI data analysis has always been an active and multidisciplinary research topic which has allowed new paradigms.

In conventional task fMRI, the subject is exposed to a stimulus or is performing a task while the blood oxygenation level dependent (BOLD) signal—a proxy for brain activity—is recorded. Given the experimental timing, a regression model can be built to be fitted to the fMRI timecourses and lead to a statistical parametric map showing where in the brain sufficient evidence for evoked activity is present. While these studies benefit from the spatial coverage and resolution of fMRI, the slowness of the BOLD response is a limiting factor to determine temporal characteristics of brain responses. Mental chronometryusing fast advanced event-related designs has been developed to measure small differences in onsets of activity in different regions, but the technique remains limited by the nature of the BOLD signal itself in terms of variability of the signal between brain regions and between subjects [2].

Increasing evidence that spontaneous activity provides information about how distributed brain regions integrate into large-scale functional networks [3], has led to a large interest from the community into “resting-state” studies where subjects can freely engage into a process of mind-wandering [4]. The analysis of these paradigm-free datasets has relied on functional connectivity that is a measure of statistical dependency between a pair of fMRI activity timecourses [5], exploratory multivariate methods such as independent component analysis, as well as graph modeling approaches.

Conventional approaches for resting-state fMRI analysis are driven by average behavior over a whole fMRI run of several minutes leading to dissociated functional networks and, therefore, they will miss important features of dynamics of network interactions [6]. Recent findings reveal that these ongoing interactions, for instance, between high-level networks during mind wandering [7], can be characterized using time-resolved analysis ∗8, 9 based on a different toolset than those of mental chronometry as any timing information is typically ignored (or absent) and network-level interactions are targeted. In this review, we discuss the state-of-the-art in time-resolved fMRI data analysis since the first reports of moment-to-moment fluctuations in functional connectivity 10, 11. While originally designed for exploratory analysis of resting-state fMRI, it is worth mentioning that these methods can be readily applied to task-based fMRI as well; e.g., see Ref. [12] for a more specific overview.

We first briefly discuss different methods to extract dynamic information from fMRI data and then specifically focus on recent methods that encode this dynamic information either through direct observational measures or by establishing brain states that can then be fed into temporal models. We demonstrate how these developments allow managing and summarizing large amounts of information contained by the dynamic characterization of brain activity. Temporal modeling of brain dynamics opens avenues towards more mechanistic models of network interactions, and how they underpin brain function and dysfunction.

Elements of temporal dynamics

From sliding-window correlations to instantaneous activity patterns

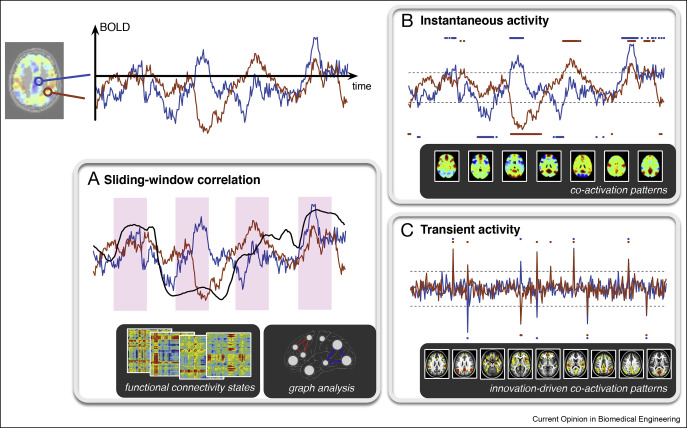
The first evidence of functional network organization from resting-state fMRI data was based on functional connectivity as measured by Pearson correlation coefficients between pairs of fMRI timeseries. Computing second-order statistics for the whole brain, considering $N_{S}$ spatial locations or regions from an atlas, leads to a symmetric connectivity matrix of size $N_{S} \times N_{S}$ , which was termed as the functional connectome. As the correlational measures reflect the average behavior during the complete fMRI run, we miss moment-to-moment fluctuations in functional connectivity that might be informative about dynamic brain processes. Therefore, functional connectivity was computed over shorter periods of time using sliding-window correlations (SWC) or time-frequency measures [10], as illustrated in Figure 1A. Windowed correlations suffer from a number of methodological issues such as limited statistical power [13] and potential spurious fluctuations induced by aliasing of low frequency components [14]. Together with 0.01–0.10 Hz bandpass filtering commonly applied in connectivity studies, faster dynamics become increasingly difficult to be captured and need to rely on carefully designed null data for statistical testing 15, 16, 17.

Instead of measuring changes in connectivity, fluctuating brain activity can also be captured using first-order statistics, that is, with time-resolved analysis of instantaneous activity patterns. Such an alternative approach mainly relies on thresholding; for instance, using the hierarchical exponentially weighted moving average method [18] to detect state changes, or the point process analysis (PPA) 19, 20 to mark timepoints whenever activity exceeds a certain level, as illustrated in Figure 1B. Detection of timepoints can also be informed about the hemodynamic response, such as in the paradigm-free mapping approach [21] where a redundant general linear model is used to recover responses to short activation events without any knowledge about the timing. The selected fMRI frames contain sufficient information to recover well-known resting-state networks similar to those obtained by independent component analysis ∗22, 23, or when applied to a seed region, the average of the selected frames is a proxy of the seed-connectivity map [24]. It is also possible to apply thresholding to other representations of the activity timeseries. Notably, using a regularized deconvolution method that incorporates knowledge about the hemodynamic system, not only the deconvolved activity-inducing signal, but also its derivative—so-called innovation signal—can be obtained [25]. The latter encodes transients in terms of positive and negative spikes for increases and decreases in activity, respectively, as illustrated in Figure 1C.

Defining brain states

Time-resolved measures do not summarize the data well. Second-order methods such as SWC even lead to data inflation as the number of measures easily exceeds the size of the original data. However, mathematically, there is no increase in information content—the matrices obtained from SWC will have a maximal rank of the number of timepoints inside the window. Therefore, there is a clear need to represent the time-resolved measures in a more compact way. One such effort is through dynamic connectivity regression to detect change points in dynamic FC [26]. Moreover, in Ref. [27], temporal clustering was applied to define FC states of which transition behavior could then be studied. As an alternative to mutually exclusive states [28], derived the eigenmodes of SWC measures that can superpose to explain the dynamic connectivity measures. It is also possible to use dictionary learning 29, 30, which allow to control the number of overlapping states. A different avenue is to extract graph topological properties from the SWC measures and then analyze brain organization in terms of information transfer, efficiency, and structure. Such an approach was applied to study the impact of learning at different timescales from hours to minutes [31]. At a faster timescale [32], observed brief intervals of high global network efficiency. In a similar method [15], found periods of high and low modularity that can be tracked over time [33]. It is worth mentioning the recent debate about whether dynamic changes or switchings of brain states produced by SWC are ascribed to small sample size and non-linearity rather than weak non-stationarity in the statistical sense per se ∗13, 16, 34. In any case, the application of these approaches has revealed alterations in fluctuations of brain activity in several disorders, such as multiple sclerosis [28], autism spectrum disorder [35], schizophrenia and bipolar disorders 36, 37, see Ref. [38]for an extensive review including issues related to spatial atlasing and [39] for another review focusing on potential contribution and interpretation of patterns recovered by time-resolved analysis.

Also first-order methods require an additional step to summarize information as the number of timepoints retained by the thresholding step—either on the original timeseries as in PPA or on innovation signals (see Section 2.1)—can be relatively high and spatial patterns at individual time frames can be very noisy. The predominant approach here is to apply temporal clustering. For instance, co-activation patterns (CAPs) are the spatial representatives of temporal clustering applied to the marked timepoints [24]. This technique was originally applied to a seed region such as the posterior cingulate cortex, but it was also further extended to whole-brain analysis [40]. As the CAPs can be obtained per run or subject, one can then apply spatial analysis; e.g., Ref. [41] studied different states of consciousness. However, more relevant to reveal differences in dynamics, CAPs-derived temporal measures such as occurrence percentage, duration, or state switching frequency can be obtained; e.g., to show differences during a working-memory task [42]. Temporal clustering of innovation signals as introduced before allows identifying reoccurring patterns of transient activity, termed innovation-driven co-activation patterns (iCAPs) [8]. The main advantages of working on transient representation of the fMRI data are twofolds: (1) networks with temporally overlapping activity, but different transients, will be disentangled and (2) spatial patterns representing each transient will be less noisy thanks to the previously applied regularization step. Once the repertoire of iCAPs established, spatiotemporal regression on the activity-inducing signals then recovers the networks' timeseries that are free from hemodynamic blur.

Another attempt to define spatially overlapping but temporally distinct activity patterns, referred to as temporal functional modes (TFMs), was proposed by Ref. [43] through successive application of spatial ICA and temporal ICA (tICA) to a rich fast-fMRI dataset. However, this framework generated temporally isolated networks, potentially regarded as neuroscientifically implausible, due to tICA's inherent independence assumption. The TFMs were later greatly refined by using a generative probabilistic model, accounting for between-subject variability and hemodynamic response function, to produce spatially and temporally overlapping networks, termed probabilistic functional modes (PFMs) [44].

Towards models of large-scale brain dynamics

Brain states summarize the large amount of time-resolved measures—either from first, or from second order statistics—in an effective way, and can then be used to track network dynamics in terms of occurrence, frequency, duration, switching statistics, or other related metrics ∗8, 27, 45. These features are driven by fast changes of activity that underlie brain function, and thus provide an important new avenue to observe large-scale network dynamics and initiate new, biologically more plausible, hypotheses about brain processes. However, testing more complicated notions of network coupling and interactions, as well as their alterations, requires generative and computational temporal models to systematically examine the richness of the brain dynamics.

Several related lines of research have been followed without the explicit use of time-resolved measures. For instance, dynamic causal modeling is attempting to capture interactions between multiple brain regions by fitting state-space models with biophysically informed observation and state equations [46]. Another important effort is to use structural brain connectivity from diffusion-weighted MRI to inform large-scale neural models 47, 48, 49 that can then be used to simulate functional data and derived measures. This way, structure–function relationships can be investigated and validated. Recent work has also proposed control-theoretical analysis of structural networks to establish control nodes and study functional networks and transitions between them in terms of reachability [50].

The work that we would like to highlight particularly in this review is incorporating brain states to understand dynamic processes such as the transitory roles of large-scale networks [51]. For instance, task-positive networks that are associated with basic cognitive tasks and -negative networks are anti-correlated based on several minutes of resting state [52]; however, the dynamic behavior of these networks is much more intricate than a naive interpretation of such correlation would suggest. Indeed, iCAPs analysis showed that the default-mode network—i.e., the most prominent resting-state network related to self-referential processes—and fronto-parietal networks, which are related with attentional processes, actually co-activate together, while sub-networks support the appearance of the anti-correlation signature [8]. Revealing complex dynamic interactions is the first step towards more accurate representations of behavior.

A systematic assessment of temporal sequences and interactions of large-scale networks can be pursued using temporal models such as hidden Markov models (HMMs) depicted in Figure 2A. In particular, the HMM framework has been applied for covariance states in terms of a sparse basis of co-activation patterns [53]. Similarly, SWC measures have been fed to HMMs to study the temporal characterization of network topology in temporal-lobe epilepsy [54]and post traumatic stress disorder [55]. In Ref. [56], network states of a HMM were used to study brain maturation in terms of dynamic community structure. Temporal models can also be applied to fMRI activation frames directly. HMMs have been used to model sequences of activity 57, 58, including validation on large numbers of subjects [59]. The activation patterns characterizing the HMM states are typically mixtures of intrinsic functional networks due to temporally overlapping activity. Therefore, an alternative approach inspired by bioinformatics [60] has been to use transient activity from the iCAPs framework as the input to a set of parallel but sparsely coupled HMMs [61], which then allows to explicitly capture modulatory influences instead of picking them up as mixture activity (Figure 2B). It should be noted that although fitting HMMs using expectation maximization is capable to estimate brain states without temporal clustering, in many approaches, the brain states are either kept fixed, or initialized by a clustering step. Finally, we also mention a recent approach from statistical mechanisms, where local minima in an energy landscape driven by entropy form attractor states [62], as illustrated in Figure 2C.

Dynamic viewpoint to advance insights into brain organization

Whole-brain coverage of fMRI has enabled a systems-level approach to brain function, where the recent advances to characterize dynamic behavior added new compelling prospects. These developments not only serve for resting-state fMRI, but also for task fMRI, especially during more ecological paradigms such as movie watching or self-controlled tasks. An essential point, as illustrated in Figure 3, is to link the computational models with relevant neuroscientific questions, where the measures and model should be at the corresponding level of abstraction. The availability of additional behavioral, neuropsychological, or clinical data should further refine and guide these model designs.

One fundamental question that can be reframed in terms of dynamic network interactions is how the brain supports coordinated cognition by linking perception, attention, goal-directed thought, as well as learning [31]. Another one is how adaptation to an ever changing environment can be understood by flexible network organization. The triple-network model states that a particular balance between salience, executive control, and default-mode networks is required [63], and that disbalances can be linked to cognitive deficits in several disorders. Recently, Ref. [7] suggested a dynamic perspective for spontaneous thoughts in terms of continuously interacting networks, a viewpoint that has been studied quantitatively from childhood to adulthood [56], and with respect to attention to pain [64] and major depression [65].

The fMRI BOLD signal is an indirect and slow hemodynamic surrogate of neuronal signal, and thus progress in the biophysics of the spatiotemporal hemodynamic response and separating various factors contributing to BOLD remain essential for future fMRI data analyses 66, 67. At this point, both more advanced fMRI acquisition schemes as well as complementing with other neural signals such as electroencephalography (EEG) or intracortical recordings, where the question remains which of their features—e.g., oscillatory 68, 69, 70or scale-free behavior 20, 71—are most meaningful to complement time-resolved fMRI measures. Even molecular mechanisms such as gene transcription patterns ∗∗72, 73 or cerebral Aβ measured by positron emission tomography [74] can be incorporated as data becomes available. Ultimately, we expect such research to contribute to better integrate information at various scales and to close the gap with models of large-scale cortical systems from computational neuroscience ∗∗72, ∗75, ∗∗76 (Box 1).

Box 1

Critical questions about the importance of modeling brain dynamics.

•
What are the best time-resolved measures to characterize ongoing fluctuations of brain activity?
•
How do network interactions support essential features of brain function such as coordinated cognition, learning, or stability in a changing environment?
•
How are network interactions altered in neurological disease and disorder, and can these be used for diagnosis and prognosis?
•
How do dynamics measured using fMRI BOLD relate to other non-hemodynamic neural signals such as EEG and their fast temporal features such as oscillatory behavior?

Perspectives

We have highlighted the development of new measures and models of brain function that will benefit from the dynamic viewpoint. Next to providing new insights into network organization, several other perspectives are worth mentioning. First of all, dynamic network models can be used to improve strategies of neurostimulation or neurofeedback [77]; for instance, real-time fMRI is typically used to feed back the activity level of a single brain region [78], while network measures could target more relevant large-scale interactions [79]. Second, resting-state fMRI has raised hopes of defining imaging-based biomarkers for early diagnosis and prognosis of neurodenegerative and neurodevelopmental conditions ∗∗80, 81, 82. Combined with massive MRI data acquisition & sharing initiatives [83], better models capturing accurately dynamic processes can become the cornerstone to reach this ambitious aim.

Conflicts of interest

None declared.

Acknowledgments

This work was supported in part by the Swiss National Science Foundation(grant #205321_163376) and in part by the Bertarelli Foundation.