A new concept of edge shrinkage, case deduced from the treatment of Pet-Al residues of post-consumed food cartons with an alkaline solution

1. Introduction

Aseptic composite packaging materials are mainly composed of paper, aluminum and low density polyethylene plastics (LDPE). Food brick-type packaging generally contains 75% fiber, 20% LDPE, 5% aluminum (Robertson, 2021). The aluminum-plastic laminates of the packaging structure are formed by a high frequency and hot pressing process, which tightly bonds layers of aluminum and plastic (Dahai et al., 2015). After being consumed, the aluminum-plastic composite is difficult to be separated or broken down effectively into elementary components. The fibers can be extracted from these post-consumed aseptic packaging by hydraulic dissociation. Reinforced aluminum-plastic laminates can be separated by various recycling approaches such as acid or basic treatment as demonstrated (Zhang et al., 2014). However, treatment in a basic medium requires monitoring the behavior of the OH− anion in the solution concerned, thus giving rise to different forms of possible aluminum hydroxide; in our case the study is focused on the OH− coming from sodium hydroxide compared to that of potassium hydroxide. Based on previous studies (Liddell, 2005), the shrinking core model is considered as the most suitable to describe the kinetics model for the shrinking process of metal ions (Safari et al., 2009). The shrinking core process is a heterogeneous process that involves several fundamental steps (Wesenauer et al., 2020) that are simultaneously involved and affect each other. Those steps are the diffusion step through the liquid film layer, the diffusion step in solid, and a chemical reaction step. As evidence and consideration, other results indicate that the shrinking core model was not suitable for using an organic solvent in the leaching process (Wanta et al., 2018) and to illustrate his real phenomenon (Wanta et al., 2020). The study made by Wen (1968), which is based on Shrinking-Core model for the slab model, shows that a symmetrical diffusion of the reagent occurs through the two sides of large bare surfaces. The extension made by Levenspiel (1998) (for the flat shape cannot be used in our case (aluminum stacked between two sheets of polyethylene) since polyethylene (plastic) has a different behavior towards reagents reacting with aluminum. For that, the basic treatment suggests another mode of attack which takes into account the impermeability of the polyethylene layer to OH− hydroxide. In this study, we investigated for a new model which obeys this particular case, we devised a mathematical equation that is able to illustrate the real physical phenomena of the shrinking process. This mathematical model is derived from the modification of the shrinking core model.

2. Experimental study

2.1. Materials and products

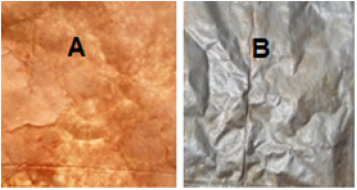
The Pet-Al residue was separated from the cardboard by simple pulping with distilled water at room temperature Fig. 1(A). In reality the adhesive used during the manufacture of food bricks such as polyethylene-co-methacrylic acid (EMAA) causes an increase in viscosity on the one hand and ensures the attachment of the layers on the other hand (Lopes and Felisberti, 2006), therefore we need to gently scrape the Pet-Al residue to remove the thin cardboard still attached to one of the two sides Fig. 1(B), it was washed, then dried and cuted according to the size of a square of 1 cm/1 cm with mass M = 6.5 mg and according to the dimension of a square of 5 cm/5 cm with a mass M = 162.5 mg using a Kern type precision balance (0.001 g). We prepared six reagents of NaOH (Novachim) and KOH (Panreac) with concentration of 1M, 2M, 4M, 6M, 8M and 10M; the titrating solution was hydrochloric acid HCl 1M (SIGMA-ALDRICH 37%). The temperature was measured using a digital thermometer, the heating is done in a thermostatically controlled water bath model Stuart RE300B. By using a Metrohm 744 pH- meter the pH was saved. The microscopic structure of Rsd (Pet-Al), was determined using an ultra high resolution SEM field Thermo scientific Q250 scanning electron microscope.

2.2. Operating mode

The Rsd(Pet-Al) was introduced into test tubes with the reagents in question at different concentrations ranging from 1 M to 10 M and at temperature 20 °C, 40 °C, 60 °C and 80 °C. A volume of 50 mL of 1 M basic reference solution and the same for the residual solution (which has reacted with Rsd(Pet-Al)) was dosed by taking a volume V = 2 mL of 1 M hydrochloric acid each minute and under magnetic stirring at room temperature. The separation results were presented in terms of separation time. The separation time is the time when the layers of polyethylene and aluminum are completely separated. Each test was repeated three times.

3. Results and discussion

3.1. Separation mode

Fig. 2 shows a degradation of the aluminum layer stacked between two polyethylene layers going from the sides towards the center (centripetal degradation) resulting by action of NaOH or KOH. Therefore, we can confirm that on basic medium the attack process of aluminum compiled between two layers of polyethylene was totally different to that in acid medium. In fact, Yan et al. (2015) have recently shown that H+ ions of the methanoic acid used cause cracks on the surface of the plastic and penetrate there through (very small cation) to oxidize the aluminum.

To ensure the attack model, we analyze the surface of a sample of Rsd(Pet-Al) by SEM. Fig. 3 present pictures taken at an intermediate instant before the total separation of plastic from the aluminum. The cracks observed in an acid medium on the polyethylene layer doesn't exist proving, in our case, that the OH− anion is unable to penetrate through the polyethylene remaining the Al2O3 layer intact; the attack is done by the edges and his speed improves as we minimize the sample size.

3.2. Temperature and concentration factors

In order to see the favorable conditions of separation, we study the concentration and temperature effects on the kinetics of the reaction; we keep the same liquid/solid ratio for each test (10 mL/1pcs of 1 cm2 Rsd(Pet-Al)). The end of the reaction is marked by the total dissolution of the aluminum until separation of the plastic, the results are grouped in Fig. 4.

For the two separation reagents, two different behaviors are observed depending on whether the temperature is below or above 40 °C; indeed if the temperature is lower than 40 °C one expects a too long separation time while the duration recorded for the temperatures higher than 40 °C is much shorter. Except that, there is an anomaly for the 10M concentration of the NaOH reagent characterized by a slower speed than that of 1M. This anomaly can be due to a blockage in the dynamics of the chemical reaction caused by complexations of aluminum for the concentration values which exceed 8M in NaOH, also the consumption of the OH− ions and their generations must be taken into account consideration according to Guillaume and François (1997). We can conclude that the temperature 60 °C and the concentration 4M are the most suitable kinetic parameters for the separation, except that, for the reagent NaOH the separation time is slightly less than that of KOH. The dissolution of aluminum is not done in a single step, the corrosion kinetics of aluminum involves two processes of transfer of conjugated electrons the first between Al and Al3+ the second between H2O and H2. According to Chu and Savinell (1991) the chemical reaction at a basic pH ≥ 12 takes place as follows.2Al + 6H2O + 2OH− → 2Al(OH)−4 + 3H2

As a result, the level of dissolved aluminum will depend on several factors, including the concentration of the solution in OH− ion also the presence of [Al(OH)4]- without forgetting the temperature factor.

3.3. The OH− hydroxyl behavior

Since it is a dosage of a strong base with a strong acid, the concentration calculation suggests the application of the formula pH = 14 + log [OH−]. Fig. 5 illustrate the dosage of the residue solution obtained after total dissolution of the aluminum respectively in the basic solution NaOH and KOH, compared to a basic reference solution of NaOH and KOH.

The consumption of OH− ions is clearly observed for the two reagents, except that, the reaction time for the NaOH based solution is almost double compared to KOH. This dosage is marked by the appearance of a white precipitate as soon as we reach the 9th minute for NaOH and the 3rd minute for KOH which disappears subsequently during the dosage until waiting for the 26th minute for NaOH and 8th minute for KOH, to see the persistence of this white precipitate. Towards the last minutes of the dosage, characterized by a strongly acid pH, there is the disappearance of the precipitate and the solution again becomes clear, which proves the evolution of aluminum hydroxide to Al3+. The study of the variation of the hydroxyl concentration [OH−] by difference between the curve [OH−] = f (time) coming from the reference solution used and the solution rich in aluminate [Al(OH)4]- allows to consider reaction mechanisms explaining the passage of the aluminate solvate [Al(OH)4]- to the solid aluminate Al(OH)3. Fig. 6 represent, as a function of the dosage time, the variation of [OH−] in solution rich in aluminate [Al(OH)4]- respectively for the reagents NaOH and KOH from which the variation in [OH−] of the reference solution cited just before. This allows us to visualize the concentration evolution of free hydroxyls in solution coming only from reactions of the aluminate species in solution. According to the curves [OH−] = f (time) there are two stages, sometimes consumption, sometimes release. In the first step, the curve shows a significant decrease in [OH−], which implies the consumption of hydroxyl ions due to the formation of a charged polymer. This would therefore indicate that when a neutral monomer already existing before the dosage reaches an adequate pH value, it becomes its charged counterpart. At the 26th and 9th minute respectively for NaOH and KOH, there is an abrupt rise in [OH−] due to the release of the hydroxyl form again leads to neutralize a certain precursor of the solid hydroxide obtained.

3.4. SEM analysis

At neutral pH two phases are formed, a white phase and a second transparent phase above the first. Heating is carried out at a temperature above 100 °C. In order to get rid of the water, the white precipitate recovered was dried in an oven and then treated with SEM, see Fig. 7.

The analysis of SEM spectra in Fig. 8 and Fig. 9 shows that salts in the form of NaCl and KCl which appear accompanied by two peaks of aluminum and oxygen due to the presence of aluminum hydroxide in its possible forms from Bayerite or Gibbsite.

Indeed, the atomic percentage calculation given by SEM (Table 1 and Table 2.) of aluminum and oxygen for a compound of crude formula AlxOy gives y = 5x to that for the precipitate (a) and y = 6x for (b).

Table 1. Quantitative result of the compounds present in the precipitate (a).

Element	Net Counts	Weight %	Atom %	Formula	Compnd %
C	319	3.68	7.16	C	3.68
O	3936	23.20	33.89	O	23.20
Na	15984	25.57	25.99	Na	25.57
Al	5336	7.80	6.76	Al	7.80
Cl	24359	39.75	26.21	Cl	39.75
Total		100.00	100.00		100.00

Table 2. Quantitative result of the compounds present in the precipitate (b).

Element	Net Counts	Weight %	Atom %	Formula	Compnd %
C	491	2.97	5.56	C	2.97
O	6730	41.31	58.07	O	41.31
Na	29	0.05	0.05	Na	0.05
Al	10183	11.71	9.76	Al	11.71
Cl	15327	21.49	13.64	Cl	21.49
K	12016	22.47	12.93	K	22.47
Total		100.00	100.00		100.00

In the initial solution, the predominant aluminate species is undoubtedly the tetrahedral monomeric anion Al(OH)4-. In the final solid compound Al(OH)3, the aluminum atoms are in octahedral coordination. This change in coordination can take place either at the solid-liquid interface such Akitt and Gessner (1894) investigated, or in solution as (Moolenaar et al., 2002) studied by means of polymerized species (Myund et al., 1995) which are considered to be the precursors of the final solid form according to Renaudin and François (2006) and more detailed by Robertson (1975) Indeed, modeling by semi-empirical molecular quantum mechanical calculations on the formation heats was carried out on all possible aluminate species ranging from monomers to tetramers (Gerson et al., 1996). These calculations make it possible to highlight species liable to form in alkaline solutions of aluminates. Their model confirms Al(OH)4- as largely predominant in strongly basic solution.

3.5. Edge shrinkage concept

3.5.1. Limit of the flat shrinking-core model

The slab geometry shown in Fig. 10, generally used for the modeling of a shrinking-core, in the case of heterogeneous non-catalytic reactions described by C Y Wen. The reagent is distributed across the surface on both sides (symmetrical diffusion).

The extension of the calculations made by Octave Levenspiel especially for the flat plate gives:

The chemical conversion expression is(1)with L the half thickness gives(2)the result is:(3)(4)(5)

The case of the aluminum-plastic laminate of post-consumed food bricks represented by Fig. 11 appears as a special case of the flat model, in fact the situation seems reversed since the attack of the reagent is done only by the edges.

For this, the design of a new model that can solve this particular case is necessary, using a mathematical approach and while drawing inspiration from existing models.

3.5.2. The ʺAymen Edge Modelʺ new model

Inspired by the principle of the schrinking-core model of spherical particles with unchanged size already developed by Yagi and Kunii (1961) and which considers the fluid surrounding the solid in question as being a gas, we have launched a new model represented in Fig. 12 which applies to the particular case of the Rsd(Pet-Al) of food bricks where the aluminum plate is stacked between two plastic layers (polyethylene) called ʺAymen Edge Modelʺ.

Our mathematical approach is to transform the variable thickness for the flat shape denoted L described by CY Wen, into a constant value called thickness "e"; consequently to vary only the distance x traveled by the reagent according to a single dimension L as shown in Fig. 12.

Also, this new model visualizes the same five steps described by Yagi and Kunii which occur in successions during the reaction when a gas or liquid comes into contact with a solid, reacts with it and transforms it into a product. Such a reaction can be represented by:A(liq or gaz) + b B(solid) → products

In our case the reagent A is a solution of NaOH or KOH, the solid B is the aluminum sheet stacked between two layers of polyethylene (Pet-Al-Pet).

3.5.3. Diffusion through gas film controls

The gas film resistance check, the concentration profile for the gaseous reagent A will be shown as in Fig. 13.

According to this figure, no reagent is present on the surface of the particles, therefore the concentration of the driving force CAg - CAs becomes CAg and remains constant at all times during the reaction of the particle. Now that it is convenient to derive the kinetic equations based on the available surface, our attention is directed to the external surface Sex stable and having a thickness e assumed constant (e = cst) and of side L.

Based on the equation (6) stoichiometry we note(7)

NA number of moles of reagent A, NB number of moles of product B, or we have(8)we obtain(9)(10)

Let ρB be the molar density of solid B and V the volume of the particle, the quantity of B present in the particle is(11)

The reduction in volume accompanying the disappearance of dNB moles from the reacted solid is given by the relation(12)

We replace (11) in (12)(13)or it give(14)

The replacement of equation (14) in (10) gives the rate of the reaction in terms of shrinking distance of the unreacted core gives(15)where kg is the mass transfer coefficient between the fluid and the particle, by reorganizing and integrating we discover the way in which the unreacted core shrinks over time(16)(17)

L et τ be the complete conversion time of the particle taking x = 0 in equation (17)(18)

By combining equations (17), (18) we obtain the fractional time t for a complete conversion τ as a function of the distance x which has not reacted(19)

This can be written in terms of fractional conversion, noting that(20)(21)

Therefore equations (19), (21) gives(22)

We thus obtain the relation which links time with distance and conversion.

3.5.4. Diffusion control through the ash layer

Fig. 14 illustrates the situation in which the speed of the reaction is controlled by resistance to diffusion through the ash.

To develop an expression that links time and distance such as equation (17), we need a two-step analysis:

First examine a typical particle that has partially reacted and write the flow relations for this condition, then apply it to all the values of xc, in other words integrate xc between L and 0.

Consider a partially reacted particle as shown in Fig. 14. Reagent A and the unreacted core boundary move inward to the center of the particle. But for gas/solid systems the shrinking of the unreacted core is slower than the flow of A towards this core by a factor of about 1000, which is roughly the same ratio of the densities of the solid compared to gas. For this reason it is assumed, considering that the concentration gradient of A in the ash layer is at all times, that the unreacted nucleus is stationary.

For liquid/solid systems the ratio is closer to unity than 1000 according to Octave Levenspiel. Yoshida et al. (1975) consider a relaxation of the above hypothesis. For the Solid/gas systems the use of the stationary state hypothesis allows a great mathematical simplification in what follows, thus the speed of the reaction of A at all times is given by its speed of diffusion on the surface of the reaction, gold, or(23)(24)(25)

For convenience, the flow of A in the ash layer is allowed to be expressed by Fick's law for equimolar counterdiffusion, though other forms of this diffusion equation give the same result. Then noting that QA and dCA/dx are positive, so we have(26)where De is the effective diffusion coefficient of the gaseous reactant in the ash layer.

Often it is difficult to assign a value in advance to this quantity because the property of the ashes (its sintering qualities for example) can be very sensitive to small quantities of impurities in the solid and to small variations in the environment of particles.

Combine equations (23), (26) to obtain for all x(27)

Integration through the ash layer from L to x givesor(28)

This expression represents the conditions of a governing particle at all times. In the second part of the analysis, we will assume that the size of the unreacted core will change over time. For a given size of the core that has not reacted, the term dNA/dt is constant. However, as the core shrinks, the ash layer becomes thicker which reduces the rate of diffusion of A. However, as the core shrinks, the ash layer becomes thicker which reduces the rate of diffusion of A. Therefore integrating equation (28) with time and other variables should give the required relationship. But we note that this equation contains three variables t, NA, rc, one of which must be eliminated or written according to the other variables, before integration can be carried out. As with the diffusion film we are going to eliminate NA by writing it in terms of rc, this equation is given by equation (14) therefore replace it in equation (28). By separating the variables and integrating we get.(29)

For the complete conversion of a particle, rc = 0, the required time is(30)

The progress of the reaction as a function of the time necessary for a complete conversion is obtained by dividing equation (29) by equation (30)(31)which in terms of fractional conversion, as indicated in equation (15) becomes(32)

3.5.5. Chemical reaction control

Fig. 15 illustrates the concentration gradients in a particle as regards the control of the