1. Introduction
Road safety has been a key concern of the traveling public and the road transportation professionals alike from the day when roads were constructed for high-speed long distance travel. Besides roadway geometric design, pavement skid resistance is another highway element that has a direct impact on driving safety. Road crash investigations and historical statistical data by researchers in different parts of the world have indicated that the number of wet-weather crashes increased as pavement skid resistance decreased (Cairney, 1997; Ivan et al., 2010; Lindenmann, 2006; Merritt et al., 2015; Rizenbergs et al., 1977). The determination and prediction of pavement skid resistance has been recognized as an important requirement in the friction management of a highway network to reduce wet-weather crash risks (Crisman and Roberti, 2012; Merritt et al., 2015).
Unfortunately, owing to the relatively large number of variables involved and the difficulty in analyzing the complex relationships among the variables, attempts to solve the pavement skid resistance problem as a function of vehicle speed and water-film thickness only began to become partially successful in the beginning of 2000s (Ong et al., 2005; Ong and Fwa, 2007a; Peng et al., 2021a). Currently in highway engineering, practically in all the road safety-related formulas and analyses involving pavement skid resistance, either empirical relationships or assumed fixed values of pavement skid resistance is adopted. The uncertainties and unknown errors involved in the empirical relationships between the measured skid resistance and the influencing variables lead to unreliable skid resistance predictions. The computational tools and theoretical solutions available today are able to help address many of the problems currently encountered in pavement skid resistance determination and prediction. Compared to the existing practices, the improved skid resistance prediction analytical capability offers high potential benefits in reducing the risks of road crashes.
This paper first presents the historical background of the research and development of pavement skid resistance since the beginning of the automobile era more than a century ago. It also explains the theoretical basis and capability of the computer simulation models of pavement skid resistance developed within the last 15 years. Finally, the rationales and procedures of the application of the new computational tool in revising or improving the current pavement skid resistance-related practices are presented.
2. Historical background–pavement skid resistance research and development
The birth of the mass production automobile industry in the 1910s triggered the post-World War I surge of commercial and passenger vehicle volumes in North America and Europe, and the demand for smoother and more durable paved roads to support higher-speed travels (FHWA, 1977; Peterson, 2020; Weingroff, 2018). As more and more roads were built, the transportation professionals learned very soon that highway safety was a critical issue they could not ignore. In 1920, the National Advisory Board on Highway Research of the US National Research Council was formed, and one the “fundamental questions in highway transport” identified was “How shall safety be ensured on the roads?” (FHWA, 1977). The first National Conference on Street and Highway Safety was held in Washington DC in 1924 (Hoover, 1924). In Europe, the First International Road Congress organized by PIARC was held in Paris in 1908 (PIARC, 2021). Road safety has been a subject of major research and operational focus since then. Drivers, vehicles and highway were identified as the three key risk factors.
It took several decades for countries to gradually understand the road safety problem, and formulate strategies to improve the ability to manage the impacts of the three risk factors. In the early 1920s, the focus was on understanding, education and changing of driver behavior (Hoover, 1924). By the late 1920s, automobile manufacturers began to introduce technological improvements to enhance driving safety (FHWA, 2017). On highway design and construction, as both USA and Europe continued to expand their road networks before World War II, more and more safety improvements were incorporated, such as balanced geometric design (FHWA, 2017) and safe stopping sight distance (AASHTO, 1940).
Besides roadway geometric design, pavement skid resistance is another highway element that has a direct effect on road safety (TRB, 2011; Wambold and Henry, 1986). Providing adequate wet-pavement skid resistance has been recognized as an important measure in reducing vehicle skidding risks (Davies et al., 2005; Von Quintus and Mergenmeier, 2015). Studies have shown that improving wet-pavement skid resistance could reduce vehicle crashes by up to 30% (Cook et al., 2011; McCarthy et al., 2016). The development of pavement skid resistance test devices began as early as the late 1920s. In UK, the National Physical Laboratory has conducted research into road surface testing and the effect of skidding from 1911 until 1933 (NPL, 2021). A motor cycle and a specially designed sidecar equipped with a test wheel inclined at an angle to the direction of travel, was employed to measure sideway-force coefficient on wet experimental pavements at test speeds up to 50 km/h. The Laboratory also built a vehicle towed braking-force trailer to determine forward skid resistance by measuring the braking torque of the locked trailer wheel (Salt, 1977). The two principles of measuring skid resistance are still being adopted today by modern skid resistance test devices.
The public outcry in the 1950s and 1960s over the rising number of road casualties in both USA and Europe, led to the next period of active research into skid resistance mechanisms and the relationships between pavement materials and skid resistance. The British pendulum tester, which is currently employed worldwide for spot measurements of low-speed skid resistance of in-service pavements and laboratory fabricated specimens, was first standardized and popularized in the UK in early 1960s (Giles et al., 1962). The apparatus and test procedure was adapted from an earlier floor slip resistance tester developed in 1940s in the USA (Sigler, 1943; Sigler et al., 1948). A significant development in skid resistance studies was the extensive full-scale experimental tests carried out in USA in the 1960s by the National Aeronautics and Space Administration (NASA) and the Federal Aviation Administration (FAA) (Horne et al., 1969; Horne and Dreher, 1963; Horne and Joyner, 1965; Horne and Leland, 1962; Horne and Tanner, 1969). Major insights into the mechanisms of vehicle skidding and hydroplaning were gained through experimental measurements involving different tires, water film thicknesses, and pavement types. The effects of tire properties, pavement surface characteristics, and water-film thickness were recognized. By the early 1970s, the following characteristics of pavement skid resistance behavior under the impacts of the three main key parameters, namely tire, pavement and surface runoff, have been noted (Giles and Sabey, 1959; Horne and Joyner, 1965; Horne and Tanner, 1969; Meyer and Kummer, 1969; Moore and Geyer, 1972, 1974; Sabey, 1966).
-
(i)
Effect of water
-
•
The skid resistance of a pavement when wet is significantly lower than when dry. Routine skid resistance measurements should be made on wet pavements.
-
•
The skid resistance of a pavement measured at a given speed decreases as the water-film thickness on the pavement surface increases.
-
•
-
(ii)
Effect of vehicle speed
-
•
The skid resistance of a pavement measured at a given water-film thickness falls as the test speed on the pavement surface increases. As the test speed continues to increase, hydroplaning eventually occurs when the skid resistance becomes negligibly small.
-
•
-
(iii)
Effect of pavement
-
•
The skid resistance of a pavement is affected by the combined effects of pavement surface microtexture and macrotexture.
-
•
Owing to deteriorations in pavement microtexture and macrotexture caused by traffic polishing, the skid resistance of in-service pavements would decrease with age.
-
•
-
(iv)
Effect of tire
-
•
The skid resistance of a pavement measured at a given water-film thickness varies with the type of tire structure, tire geometric dimensions, tread pattern, magnitude of wheel load and inflation pressure, as well as the viscoelastic properties of tire rubber.
-
•
The tire-pavement skid resistance varies nonlinearly with the slip ratio and slip angle of a rolling tire.
-
•
-
(v)
Effect of environmental conditions
-
•
The viscoelastic properties of a rubber tire are temperature dependent. In general, tire-pavement skid resistance is higher when the rubber temperature is lower.
-
•
The presence of contaminants on pavement surface, such as dust, debris, lubricants, and water, etc., has a significant effect on skid resistance.
-
•
Owing to changes in environmental factors such as temperature, rainfall and other weather conditions, there are short-term (e.g., hourly, daily and weekly) and long-term variations in pavement skid resistance. For example, in temperate countries, pavement skid resistance is generally higher in winter than in summer.
-
•
The above-mentioned understanding of the characteristics of pavement skid resistance behavior were essentially derived from experimental studies and field measurements. Owing to the lack of theoretical and computational tools to solve the dynamic tire-fluid-pavement interaction, the research and studies conducted up to the beginning of 2000s have been largely confined to laboratory and field experimental works. The measured and test evidence led to the observed pavement skid resistance characteristics listed above. Numerous empirical relationships have been derived in practice based on the experimental data. Unfortunately, the inherent inadequacy of empirical relationships have to a large extent limited the pavement engineering community's ability to predict pavement skid resistance under different vehicle operating conditions.
The above-mentioned limitations could be largely addressed by solving the pavement skid resistance problem mechanistically. This became possible in the early 2000s with the emergence of high-speed high-capacity computing facilities and the availability of efficient numerical computational software for solving the coupled solid mechanic and hydrodynamic problem of pavement skid resistance. Today, a number of finite element computer simulation models have been developed by different research groups, with the capability to evaluate and predict pavement skid resistance under different vehicular operating conditions, water film thickness and pavement surface characteristics; and also to predict hydroplaning speed of a given pavement under a wet condition (i.e., thickness of water film thickness). Hydroplaning speed is the vehicle speed at which the hydrodynamic uplift becomes equal to the wheel load, and the skid resistance diminishes. Studies have demonstrated that computer simulation models were able to correctly calculate pavement skid resistance and hydroplaning speeds with good agreement with measured values (Fwa and Ong, 2008; Ong and Fwa, 2007a, b), and closely reproduce measured pavement skid resistance performance, such as variations of skid resistance with vehicle speed (Fwa and Ong, 2008; Srirangam et al., 2014), water-film thickness (Fwa et al., 2012; Ong and Fwa, 2010a, b), pavement type (Ju et al., 2013; Srirangam et al., 2014; Zhang et al., 2013a, b), vehicle or tire type (Fwa et al., 2009, 2010; Ong and Fwa, 2008), slip ratio, and slip angle (Anupam et al., 2014; Peng et al., 2021b), and temperature (Anupam et al., 2013; Tang et al., 2018).
3. Mechanisms of pavement skid resistance generation
One of the main sources of complexity of the mechanisms of friction generation at a rubber-solid contact is the viscoelastic properties of rubber. Based on past studies by researchers in the domain of rubber friction (Grosch, 1963; Kummer, 1966; Lorenz et al., 2011; Moore and Geyer, 1972, 1974; Persson, 2001), the following four mechanisms have been identified by researchers to be involved in the generation of rubber friction: (a) adhesion losses, (b) hysteresis losses, (c) cohesion losses, and (d) wear losses. Adhesion losses are the results of the energy associated with overcoming the shear resistance at a tire-pavement contact area, and the energy dissipation arising from rubber excitation caused by breaking of molecular bonds and stretching and relaxing of the rubber polymer structure. Hysteresis losses are the consequence of energy consumed in absorbing the periodic agitation of the rubber polymer structure as the rubber slides on the geometric roughness of the pavement surface. Cohesion losses occur owing to the presence of contaminants at the tire-pavement contact interface. They are the work required to break the contaminant film. Wear losses are resulted from traffic abrasive actions that rupture and remove particles from the contact surfaces of pavement and tire.
In pavement engineering, the skid resistance of a pavement is defined as the ratio of the overall resistance force Fx in the direction of vehicle movement and the normal wheel load Fy. Fx is the maximum force generated from the interaction between a moving tire and the pavement, that resist the sliding movement at the tire-pavement contact surface. Accordingly, when a vehicle is traveling at a velocity V, the skid resistance SNV generated can be calculated from the following equation.where SNV is the skid number, Fy is the wheel load normal to the pavement surface, and the total resistance force Fx in the direction of tire movement is comprised of resistance contributed from rubber adhesion force Fa, cohesion force Fc needed to break the interface contaminant bond, rubber hysteresis force Fh caused by tire deformation, and air and fluid drag force Fd.
It is noted that not all components of skid resistance force components in Eq. (1) are proportional to the applied normal load. Relating the total skid resistance forces to the applied load is not strictly meaningful or correct. In fact, it could be misleading at times in the interpretation of measured skid resistance. However, the definition of skid resistance given by Eq. (1) offers a convenient form for the studies of road vehicle driving safety in wet weather, and practical applications in the skid resistance design and testing of pavement materials.
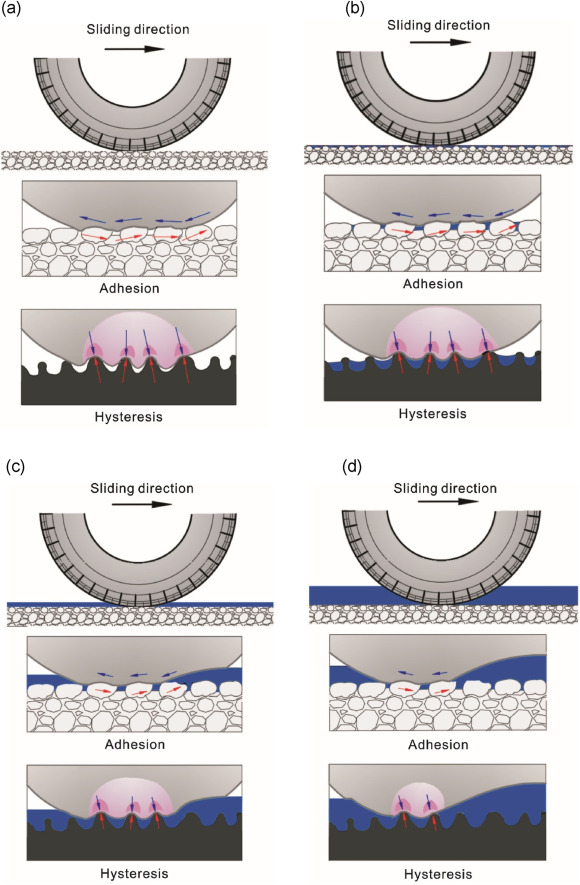
Eq. (1) is a general expression applicable for calculating the skid resistance of pavements in different condition states: dry, wetted, wet or flooded. A wetted pavement refers to a moist pavement which has been wetted, but there does not exist a continuous film of water on the pavement surface. On a wet or flooded pavement, there is a continuous layer of free water on the pavement surface. There are some important differences in the skid resistance generation mechanisms of a pavement in different states. As illustrated in Fig. 1, on a dry pavement free of contaminant, Fc and Fd are absent. Its skid resistance is derived from rubber adhesion and hysteresis (i.e., Fa and Fh). The same are true on a wetted pavement, except that the presence of moisture on the surface and water in the surface voids act to weaken the rubber adhesion force Fa and the hysteresis force Fh. This explains the abrupt reduction of skid resistance when a dry pavement is wetted.
 Fig. 1
Fig. 1On a wet or flooded pavement where there is a layer of water on the pavement surface, the presence of free water not only changes the tire-pavement contact mechanism, but also introduces an additional hydrodynamic-induced mechanism that causes tire deformations and interferes with the skid resistance generation mechanisms of Fa and Fh (Fig. 1(c) and (d)). The magnitude of interference increases as the vehicle speed is raised. Interaction between a moving tire and the surface water has the effect of developing hydrodynamic pressures that deform the tire wall and reduce the tire-pavement contact area, which in turn reduces the magnitudes of Fa and Fh. The higher the vehicle speed, the smaller the contact area becomes. The tire will eventually hydroplane when the values of Fa and Fh diminish, and the terminal SNV at the hydroplaning speed is given by the ratio of drag force Fd and wheel load Fy. When a vehicle hydroplanes, it loses both steering and braking ability.
Pavement flooded with a thick layer of water is another possible condition encountered on highways. When a vehicle travels on a pavement flooded with a thick layer of water, say having a thickness of 15 mm or thicker, the effect of fluid drag force Fd will tend to become important and the vehicle hydroplaning speed will be reduced accordingly. Under this condition, vehicles would be moving at speeds much lower than the design speed, and normal traffic operation is not possible. This condition of flooded pavement with water thickness of 15 mm or more is not normally considered in the study of skid resistance, and hence is not included within the scope of this paper.
4. Determination of pavement skid resistance
There exists a large number of empirical and statistically derived equations or models that relate various pavement characteristics (including pavement texture indices) to skid resistance (Do et al., 2013; Dunford, 2011; Dunford et al., 2008; Henry, 1986; Leu and Henry, 1983; Pomoni et al., 2020; Rose and Gallaway, 1977; Serigos et al., 2014; Siriphun et al., 2019). They provide practical guidance for selection of materials for pavement wearing courses, and pavement friction management of road networks having pavement surface materials and road operating conditions similar to those for which the empirical models were derived. However, being empirical in nature, these approaches have limited application scopes owing to the limited number of influencing parameters considered. They also add little to the body of knowledge of skid resistance generation as no mechanism of skid resistance was involved in the derivation of the empirical equations or models. In contrast, theoretical solutions are valuable in that, if available, they permit engineers to have a deeper understanding of the problem and better ability in designing and maintaining pavements for safe traffic operations. Theoretical solutions are available today to determine the pavement skid resistance at the following three pavement states: dry, wetted, and wet. Since there are differences in the mechanisms of skid resistance generation in the three pavement states, different theoretical approaches have been applied by researchers to determine the skid resistance in each state. The following sub-sections present representative theoretical solutions currently available for skid resistance determination for the three pavement states.
4.1. Determination of skid resistance of dry pavements
The skid resistance of a pavement is not normally measured in its dry state because the skid resistance of a typical dry road pavement is substantially highly than the design skid resistance demand, and skidding on a dry pavement rarely happens in real-life road operations. Dry pavement skid resistance determination is included for completeness in presentation. Compared with wetted and wet pavement skid resistance, solving the dry pavement skid resistance problem theoretically is less complex, although it is still a challenging problem computationally. Testing of the skid resistance of a pavement in its dry state is not a practice in pavement engineering. It is only done occasionally for research purpose.
4.1.1. Dry pavement skid resistance based on theories of contact mechanics
Modeling of tire-pavement friction based on theories of contact mechanics became a topic of research interest in the last century after World War II, following the dramatic increase of road vehicle volume as a result of global automobile ownership boom that started in the 1950s. However, it was not until the beginning of the 21st century that theoretical procedures for quantitative estimation of tire-pavement friction were developed. Heinrich (1997) and his fellow researchers (Heinrich et al., 2000; Kluppel and Heinrich, 2000) published a theoretical concept that relates the friction force of rubber sliding on a rigid self-affine road surface to the hysteretic energy losses arising from rubber deformations caused by road surface asperities. The basic assumption was that the dynamic damping behavior of the rubber was dependent on the texture properties of the road surface profile represented by its power spectral density. By applying the concept of fractal geometry to characterize a multiple-scaled rough road surface, they analyzed the hysteretic frictional dynamics of rubber under stochastic excitations over the rough surface, and derived a general expression of the coefficient of hysteretic friction as a function of surface texture parameters and sliding velocity.where F is the frictional force, Fn is the normal force, <zp> is the mean penetration depth of rubber into the road surface texture, σ0 is the normal stress equal to Fn divided by the nominal contact area A0, V is the sliding velocity, S(ω) is the power spectral density function of the road surface in frequency scale ω, and is the imaginary part of energy dissipation calculated from the local stresses and strains which are determined by the heights of the rough surface. The lower and upper cut-off frequency, ωmin and ωmax, correspond to the upper and lower cut-off wavelengths λmax and λmin respectively, to be determined from the road surface roughness.
In about the same period, adopting essentially a similar approach in calculating hysteretic energy dissipation of rubber, but instead of applying the notion of penetration depth, Persson (2001) proposed a concept of nominal and “real” contact area between the rubber and the substrate surface. Although the proposed contact mechanism was developed for random road surface roughness, explicit solutions were presented only for self-affine fractal surface profiles. The coefficient of hysteresis friction at sliding velocity v is given by the following equation.where wavenumber q = 2π/λ, λ is wavelength, C(q) is spectral density of rough surface, P(q) is A(q)/A(qL) = A(λ)/A(L) = A(λ)/A0, L is length of nominal contact area A0 between rubber and the road surface, ϕ is the angle between the wave propagation direction and the rubber sliding direction, ν is Poisson ratio of rubber material, V is sliding velocity, the imaginary part of the complex modulus of rubber E(ω) = E(qVcos(ϕ)). The lower and upper cut-off of integration are q0 = 2π/L and q1 = 2π/λ1, respectively, where λ1 is the shortest wavelength of the road surface roughness.
The afore-mentioned theories of hysteretic friction does not include the contribution from cohesion. Lorenz et al. (2011) suggested that the cohesion friction component could be derived from experimental measurements. Cohesion induced friction is generally considered to be insignificant at normal vehicle speed and on wet road surfaces (Heinrich et al., 2000; Persson, 2001).
It is noted that in applying either the Heinrich or the Persson approach, the determination of the actual contact area between the sliding rubber and the rough surface is dependent on the calculation of either the average penetration depth <zp> or the contact area fraction function P(q). Both <zp> and P(q) vary nonlinearly with sliding velocity, normal load, viscoelastic modulus of rubber, and road roughness parameters. The magnitudes of both are affected by the choice of the upper and lower cut-off road surface wavelengths. Studies by pavement engineering researchers indicated that to arrive at the correct calculated coefficient of friction of a road surface, a proper selection of the upper and lower cut-off wavelength is critical (Alhasan et al., 2018; Deng et al., 2021; Kanafi and Tuononen, 2017; Pratico et al., 2021).
It is recognized that under typical wheel loads of passenger cars and trucks, tire-pavement contact would occur mostly along the upper portions of the top asperities (Almqvist et al., 2011; Deng et al., 2021; Heinrich, 1997; Kanafi and Tuononen, 2017; Kluppel and Heinrich, 2000; Lorenz et al., 2011; Persson et al., 2005b). In the case of asphalt and concrete pavements, the depth of penetration would vary with the mix design of the surface course, including the type, size and gradation of the aggregates used. Since road surface roughness would deteriorate under traffic abrasive actions, the depth of rubber penetration would also vary with the degree of wear and polishing suffered by a road surface. Unfortunately, even with the knowledge of all the influencing factors (i.e., sliding velocity, normal load, viscoelastic modulus of rubber, and road roughness parameters), the current theories of contact mechanics are unable to determine the depth of penetration and actual area of contact. Studies on common road pavement materials have found that the depth of penetration ratio could vary from 10% to 50% (Deng et al., 2021; Kanafi and Tuononen, 2017; Pratico et al., 2021). Hence, to determine the sliding coefficient of hysteresis friction of rubber on a road surface, a calibration procedure involving experimental determination of the coefficient of friction is necessary to estimate the depth of penetration and area of contact for a given set of rubber and road roughness conditions.
Heinrich and Klüppel (2008) and Persson (2011) had both extended the rubber contact theory to study the sliding friction of vehicle tires on road pavements. Persson proposed a two-dimensional mass-spring tire model together with his rubber friction model to calculate the speed-dependent coefficient of friction for different slip ratios during braking and/or cornering. Heinrich and Kluppel applied a brush model for sliding tires to analyze the load dependency of sliding friction coefficient under different slip ratios during cornering and braking.
The dependency of rubber friction on temperature and sliding velocity has an important effect on the magnitude of tire-pavement friction generated. Heat is generated in a sliding rubber locally at the contact asperities. When rubber begins to slide on a pavement at a low speed, friction increases due to rubber hysteresis caused by sliding movement on unevenness of pavement surface texture. However, as the sliding speed increases, there exits a heating effect caused by the phenomenon of rubber glass transition, and it tends to reduce rubber hysteresis (Heinrich, 1997; Kluppel and Heinrich, 2000; Persson, 2006). On road pavements, the normal operating speeds of vehicles is more than one order of magnitude higher than the sliding speed at which the peak rubber friction occurs. Hence, within the range of vehicle speeds relevant for the study of skid resistance of road pavements, the effect of rubber glass transition must be considered. Overall, as depicted in Fig. 2 which shows the variation trends of measured skid resistance with speed, dry pavement skid resistance may or may not decrease with speed. Whether or not skid resistance would decrease with speed depends on the net magnitude of hysteresis friction generated.
 Fig. 2
Fig. 24.1.2. Dry pavement skid resistance by test measurements
Skid resistance testing of dry road pavement is rarely performed in practice. This is because the dry skid resistance of a typical pavement would far exceed the maximum skid resistance required for safe driving. The skid resistance requirements of a pavement is governed by its skid resistance performance under wet-weather conditions. All standard skid resistance tests are conducted on wet pavements with a layer of applied water of 0.5 or 1.0 mm thick (ASTM, 2015c; BSI, 2000, 2006; FAA, 2016). If for any reason the dry skid resistance of a pavement is to be tested, it can be measured using one of the standard test methods without applying water. Standard wet skid resistance test methods are described in Section 4.3.3 “Measurements of wet pavement skid resistance”.
4.2. Determination of skid resistance of wetted pavements
A wetted pavement is characterized by the presence of water molecules on its surface and trapped water in its surface voids. This state of pavement condition, like the case of dry pavement, does not represent the most critical pavement operating condition, and is not the condition state at which traffic-speed skid resistance testing of in-service pavements is conducted.
4.2.1. Wetted pavement skid resistance based on theories of contact mechanics
The techniques of calculating the coefficient of hysteresis friction of a pavement from its surface texture characteristics based on rubber-pavement contact mechanics, as presented in Section 4.1.1, can also be applied to predict friction of wetted pavements. According to Persson et al. (2005a), Hartikanen et al. (2014) and Kienle et al. (2020), the presence of trapped water would affect the depth of penetration into the rubber by texture asperities, and the actual tire-pavement contact area. By appropriately selecting the cut-off depth in the calculation of the actual contact area, it was found that a good prediction of the coefficient of hysteresis friction could be achieved for a wetted pavement. As in the case of dry pavement, a calibration analysis against actual measured tire-pavement friction is necessary for the determination of an appropriate cut-off depth. The value of appropriate cut-off depth depends on the characteristics of pavement surface texture, properties of the rubber, and the degree of wetness.
It is appropriate to mention at this juncture that although the wetted skid resistance calculated using the contact theories would decrease as the sliding speed increases, the rate of skid resistance reduction is essentially caused by hysteresis losses of the tire rubber. This rate of skid resistance loss cannot be applied to the case of a wet or flooded pavement (Section 4.3). The presence of a layer of free water on a wet or flooded pavement would generate hydrodynamic effects due to a dynamic tire-water-pavement interaction when a tire moves on the pavement surface. The dynamic tire-water-pavement interaction mechanism is totally different from the tire-pavement contact mechanisms presented in this section.
4.2.2. Measurements of wetted pavement skid resistance
Skid resistance measurement is as a rule not performed on a wetted pavement, just as it is not normally conducted on a dry pavement. Standard skid resistance tests are performed on a wet pavement covered with a thin film of water. A wetted pavement with only some water trapped within its surface voids, though having reduced skid resistance compared with its skid resistance in the dry state, would still over-estimate the skid resistance of a wet pavement. In addition, there are two further reasons that make skid resistance measurement of wetted pavement impractical: (i) rubber-pavement friction fell considerably as the degree of wetness increases (Qian et al., 2016), where wetness refers to the degree of saturation of water in the surface voids; (ii) there is no easy practical way of measuring the degree of wetness of a wetted pavement.
4.3. Determination of skid resistance of wet/flooded pavements
The wet or flooded skid resistance of in-service pavements is of a major concern in pavement engineering. Standard skid resistance measurements are conducted with a pre-specified water film thickness (ASTM, 2015c; BSI, 2000, 2006; FAA, 2016). Besides physical measurements, the ability to correctly predict the variation of wet pavement skid resistance with vehicle speed, water film thickness, pavement surface properties, tire type and wheel load is an important requirement for driving safety management of highway road networks.
4.3.1. Wet pavement skid resistance based on theories of mechanics
The presence of a layer of water on a wet pavement means that the rubber-pavement contact theories, described earlier for friction determination on dry and wetted pavements, are no longer applicable in tire-pavement skid resistance determination. In the present case, the pavement surface is saturated and submerged in a layer of water, the dynamic interaction of tire, flowing water and pavement surface texture presents a highly complex contact situation. This complex tire-fluid-pavement interaction could not be explained by the contact theories presented in Sections 4.1 Determination of skid resistance of dry pavements, 4.2 Determination of skid resistance of wetted pavements. Typically, during an acceleration phase of a road vehicle, the tire-pavement contact area continues to decrease as the vehicle speed increases, as illustrated in Fig. 3. The reduction in tire-pavement contact area is due to hydrodynamic uplift pressure build-up in the water trapped between the tire and pavement surface, which causes the tire rubber to deform and separate from the pavement surface. The uplift pressure increases in magnitude as the vehicle speed picks up, thereby resulting in decreasing tire-pavement contact area in the process.
 Fig. 3
Fig. 3A different set of theories of mechanics, including theories of hydrodynamics and solid mechanics, is required to solve the problem of wet pavement skid resistance. The first systematic attempt by pavement engineering researchers to solve numerically for a theoretical solution of the wet-weather pavement skid resistance and/or hydroplaning problem, taking into consideration the pavement surface characteristics, was made by the research group at the National University of Singapore (NUS) (Fwa and Ong, 2008; Ong et al., 2005; Ong and Fwa, 2007a, b). The NUS research group applied commercial finite-element software ADINA (2005) to solve the tire-fluid-pavement interaction problem numerically. The computer analysis produced predicted results in good agreement with field measured skid resistance and hydroplaning speeds. Other commercial finite-element software, such as ABAQUS (2010) and ANSYS (2009), have been subsequently employed by other researchers successfully in solving the wet pavement skid resistance problem (Anupam et al., 2013; Liu et al., 2019; Peng et al., 2021b; Srirangam et al., 2014; Zhang et al., 2013a, b; Zheng et al., 2018).
The key to calculating the available skid resistance to a vehicle traveling on a wet pavement is to correctly and accurately solve the tire-fluid-pavement interaction problem involving a moving tire rolling and/or sliding on a pavement covered with a thin film of water. It has become feasible today for researchers in general with the widely available efficient computational fluid dynamics software and powerful computing facilities. Computer based 3-dimensional computational fluid dynamics (CFD) analysis employing the full Navier–Stokes equations has become a relative common tool for solving the turbulent flow field involved in the wet pavement skid resistance and hydroplaning problem. For example, Ong and Fwa (2007a, b) applied a 3-D finite volume model based on the Navier–Stokes equations, and the turbulence flow model in terms of the turbulent kinetic energy (k) and rate of dissipation of turbulent kinetic energy (ε) using the standard k-ε method, integrated with a fluid–solid interaction (FSI) approach, to simulate tire-fluid-pavement interaction and calculate hydroplaning speed and skid resistance at different vehicle speeds.
There are three sub-models in finite element simulation modeling of the wet pavement skid resistance problem, namely the tire, fluid and the pavement sub-models. Fig. 4 presents input and output variables of the three sub-models, and the flow of processed information among them. Table 1 presents a summary of the input variables required for the simulation analysis. The interaction among the three elements causes the pneumatic tire wall to deform, which in turn leads to changes in the tire-pavement contact area (i.e., the shape and area of the tire footprint) as shown in Fig. 3. Fig. 5 shows the finite element mesh of a skid resistance simulation model. As accurate determination of tire deformation is critical to the calculation of skid resistance, the complete structural elements of a tire is fully represented in the tire sub-model. As shown in Fig. 5, the structural elements include the ply, belt, double bead, rigid metal rim, and rubber components of tire tread, sidewall, inner liner, filler, and chafer. Surface membrane elements with embedded rebar layers are employed to model radial ply and layered steel belts. In view of the complex structure composition of a vehicle tire, a carefully conducted full-scale calibration of the tire's load–deformation characteristics is essential to the correct simulation of tire-pavement skid resistance.
 Fig. 4
Fig. 4Table 1. Input parameters for mechanistic tire-pavement-fluid interaction analysis.
| Pavement parameter | Environmental and vehicle operating condition | |
|---|---|---|
| Vehicle parameter | Environmental parameter | |
|
|
|
|
|
|
|
||
|
||
|
||
|
|
|
|
|
|
|
|
|
|
||
 Fig. 5
Fig. 5Due to the large difference between the elastic moduli of typical pavements and vehicle tires, pavements are without exception modeled as a rigid surface in skid resistance studies. The interaction between pavement and surface water, and that between tire and pavement, are straight forward. However, the dynamic interaction between a rotating tire and flowing water is computationally complex, requiring a “two-way coupling” solution procedure which is an iterative process to couple the responses of the fluid and tire sub-models. To save computer simulation time, instead of modeling a tire rolling on a pavement, the rolling tire is taken as the frame of reference. That is, an angular velocity is applied to the tire, and a layer of water and the pavement are given a linear speed moving toward the tire. In the computer simulation, the method of Coupled Eulerian–Lagrangian (CEL) is employed to model the interaction between the Eulerian fluid and the rotating Lagrangian tire.
The pavement sub-model is often represented by a solid plane surface in the skid resistance simulation models today. This is unsatisfactory as it does not realistically represent the actual surface texture of a pavement. An important outcome of the computer skid resistance simulation analysis is the frictional force generated at areas where the tire is in contact with the pavement. The magnitude of the contact frictional force is a function of the values of coefficient of friction, the actual contact area, and the actual normal contact force, all of which are dependent on the vehicle speed, water film thickness, water pressure, wheel load, and the pavement microtexture and macrotexture. According to Fig. 4 and Table 1, the determination of wet pavement skid resistance requires input information on pavement properties in the form of pavement surface microtexture and macrotexture, and the coefficient of kinetic friction between tire and pavement under a submerged condition. Pavement surface microtexture and macrotexture would affect drainage of surface water under a rolling tire, as well as the magnitude of the coefficient of tire-pavement friction. Drainage and friction coefficients are two key pavement properties that affect the wet skid resistance performance of a pavement. Unfortunately, the large range of geometric scale ranging from the order of μm of pavement microtexture to more than 1 m in the diameter of a truck tire presents a critical modeling problem. It is not only impractical, but also theoretically infeasible currently to model pavement microtexture using the finite element method. This explains why pavement is represented by a solid plane surface in finite element simulation of pavement skid resistance. Hence, other measures are required to model the effects of pavement microtexture and macrotexture in the finite element simulation analysis in order to correctly solve the wet pavement skid resistance problem. Some of the measures that have been adopted by researchers are described in the next section.
4.3.2. Prediction of wet pavement skid resistance performance
It has been noted in the preceding section that finite element skid resistance simulation models are unable to include pavement microtexture and macrotexture in the pavement sub-model. That is, it is unable to directly model mechanistically the effects of pavement texture on water drainage, and the generation of tire-pavement kinetic friction. The drainage effect of pavement texture is customarily represented through surface roughness indices such as Manning roughness coefficient (Reed and Kibler, 1983), and roughness height and roughness constant (NCHRP, 2021) in fluid flow analysis. This has been an accepted practice in pavement engineering, and can be conveniently incorporated into a skid resistance simulation analysis, provided that values of appropriately calibrated roughness indices are available for the common range of pavement texture profiles encountered.
Compared with the representation of drainage effect of pavements, the determination of the input value of coefficient of wet kinetic friction is much more complex. Two main approaches have been adopted by researchers for this purpose. The first approach directly provides as an input an estimated value of friction coefficient, often as a function of vehicle speed. Such a function can be obtained experimentally by performing dynamic friction tester (DFT) tests at different speeds on a test surface (Hu et al., 2016; Wasilewska et al., 2016). This method does not consider the influence of water thickness and hydrodynamic effect. Several studies applied Persson's contact theory of rubber friction (Sections 4.1.1 Dry pavement skid resistance based on theories of contact mechanics, 4.2.1 Wetted pavement skid resistance based on theories of contact mechanics) to calculate the coefficient of hysteresis friction as the input value to skid resistance simulation analysis (Liu et al., 2019; Zhu et al., 2017, 2021). According to Persson et al. (2005a), this is applicable at low vehicle speed lower than approximately 30 km/h when there is sufficient time for surface water to be squeezed out from the tire-pavement contact area. However, at higher vehicle speeds, the friction coefficient would be over-estimated due to the presence of hydrodynamic pressure and nonlinear deformations of tire walls. Furthermore, the tire-pavement contact area may be fragmented and not continuous in the case of ribbed tires. Besides physical measurements of pavement microtexture and macrotexture, this method also requires experimental calibration of problem parameters, such as the ratio of actual contact area, that are dependent on the characteristics of pavement texture.
The second approach is the back-calculation method first proposed by the research group at the National University of Singapore (Fwa and Ong, 2008). This NUS back-calculation method has been validated using actual field measured skid resistance data of various modes of vehicle and aircraft operations (Fwa and Chu, 2021; Ju et al., 2013; Ong and Fwa, 2010a, b; Pasindu et al., 2011; Peng et al., 2021a). The concept of the approach is based on the understanding that the skid resistance of a wet or flooded pavement is dependent on its microtexture and macrotexture. According to the Penn State model proposed by researchers at the Pennsylvania State University (Henry, 1986; Leu and Henry, 1983), the kinetic friction of a wet pavement can be expressed as a negative function of vehicle speed with two parameters of pavement texture characteristics, as given by the following equation.where is the coefficient of kinetic friction at speed V, is the initial coefficient of friction when the relative sliding begins, which is given by the intercept at V = 0, and β is a regression constant. Both and β are to be estimated from experimental data. Research studies have found the exponential decay function of Eq. (4) to be a representative deterioration trend of the dynamic friction coefficient between rubber and a large class of materials (Kuwajima et al., 2006; Oden and Martins, 1985).
Experimental studies have shown that on a given pavement covered with a known thickness of water film, field measured skid numbers fitted well with Eq. (4); and that the terms μ0 and β were highly correlated with pavement texture related indices (Hall et al., 2009; Henry, 2000). μ0 was found to be highly correlated with pavement microtexture; while β which is related to the rate of change of coefficient of friction with speed V, was found to be closely governed by pavement macrotexture. According to ASTM standard E274 (ASTM, 2011), skid number SNV at speed V is defined as 100 times the measured friction coefficient defined as follow.where F is the horizontal tractive force applied to the test tire, and W is the vertical load on the test tire.
Other statistical regression relationships similar to Eq. (4) have been proposed by researchers. Such relationships can also be used for the purpose of the back-calculation analysis. For example, adopting the exponential decay function, the deterioration trend of rubber-wet pavement contact friction from an initial to a terminal , can be represented by the following expression (Kuwajima et al., 2006; Oden and Martins, 1985).
The value of can be taken as (SN0/100) on the understanding that at very low test speed, the hydrodynamic effect of surface water is negligible and there is sufficient time for water to be squeezed from the tire-pavement contact. The terminal has the value of zero theoretically at the hydroplaning speed of the wet pavement concerned. Hydroplaning refers to the state of tire-pavement contact when the hydrodynamic uplift acting on the tire increases and becomes equal to the wheel load. Under this condition, the tire loses contact with the pavement and the driver would lose steering (i.e., directional) and braking control. In actual field measurements, the practical hydroplaning phenomenon would take place before the theoretical value of zero, due to the presence of fluid drag force. A small friction coefficient of the order of 0.05 may be chosen (Agrawal, 1983; Pasindu et al., 2016; Zhu et al., 2021), as shown schematically in Fig. 6.
 Fig. 6
Fig. 6The flow diagram in Fig. 7 shows the steps involved in the application of the back-calculation approach in the finite element skid resistance simulation analysis. As there are two unknowns in either Eqs. (4) or (6), at least two skid resistance data measured at different test speeds are required for the back-calculation analysis. Although the analysis involves a trial-and-error process, the problem is well behaved and with an appropriate initial choice of , a good match between the predicted and measured skid resistance could be achieved in less than four or five trials. A good initial choice of can be taken as (SN0/100) where a good estimate of SN0 can be made from the two skid resistance data, which are typically measured at the test speeds of 48 and 64 km/h. Alternatively, though not practically feasible in most field operations, SN0 can be obtained from a low-speed skid resistance test, such as the British pendulum test as explained in Section 4.3.3.
 Fig. 7
Fig. 7The back-calculated input parameter μ0 represents largely the effect of pavement microtexture on tire-pavement contact friction, although the presence of pavement macrotexture effect could not be ruled out, especially on rough-textured or grooved pavement surfaces (Fwa et al., 2003; Han et al., 2020; Liu et al., 2004). The other back-calculated input parameter β represents the deterioration rate of with vehicle speed V. This speed dependent deterioration of contact friction, together with the hydrodynamic effect of surface water related to pavement macrotexture, contributes to the overall deterioration of skid resistance SNV with vehicle speed V.
After the input parameters related to pavement texture have been calibrated by means of the back-calculation method, the finite element skid resistance simulation model can be applied to predict the wet skid resistance of the pavement concerned under any speed, water film thickness, slip ratio, and slip angle. Fig. 8 illustrates schematically the family of skid resistance curves that can be obtained from the calibrated simulation model of a given pavement.
 Fig. 8
Fig. 8This back-calculation based approach of computer simulation of wet pavement skid resistance has been validated by research studies for different vehicle and aircraft types operating under different wet pavement conditions, based on a large number of full-scale field test data reported in past experimental studies. Fig. 9 shows graphically examples of validation on measured skid resistance data obtained by past research studies. These studies indicate that the finite element simulation modeling together with the back-calculation calibration method presents a practically reliable method for the determination and prediction of wet skid resistance of a pavement.
 Fig. 9
Fig. 94.3.3. Measurements of wet pavement skid resistance
There is a large variety of skid resistance measuring devices in use today. They can be classified into two broad categories based on their test speeds: continuous friction measuring equipment (CFME) for high-speed skid resistance testing, and low-speed skid resistance testers. A CFME which measures pavement skid resistance at a speed normally within the range of 40 km/h to as high as 100 km/h, is suitable for pavement skid resistance surveys at road network level. The low-speed testers are useful for either spot or short-distance testing of in-service pavements, or testing of small-size laboratory fabricated specimens of pavement mixtures. A test performed with a given CFME tester is normally conducted with a pre-set test speed, slip ratio, slip angle, and water film thickness. These pre-set conditions are not necessarily the same among different types of CFME. Furthermore, each type of CFME has its own tire size, tire load, magnitude of frictional force generated and method of measuring the frictional force. Therefore, the measured skid resistance values reported by different types of CFME are not equivalents, and they should be used independently of each other in skid resistance or driving safety analysis. Table 2 summarizes the main operating features of selected CFME devices.