GNSS meteorology in Egypt: Modeling weighted mean temperature from radiosonde data

1. Introduction

The radio signals propagate from Global Navigation Satellite Systems (GNSS) are delayed by neutral atmospheric water vapor. Information on delays has enabled the application of GNSS to study the diurnal variation of precipitable water vapor. The weighted mean temperature of water vapor (Tm) was used for estimating the integrated water vapor (IWV) or equivalently precipitable water vapor (PWV) from the zenith-wet delay (ZWD). The amount of water vapor per unit area is IWV while the height of the equivalent column of the liquid water represented is PWV by (e.g. [3]):(1) $P W V = I W V / ρ$ where $ρ$ is the density of liquid water.

The main method to compute PWV from GNSS is the multiplication of ZWD by the conversion factor $π$ which is a function of weighted-mean temperature (Tm). Therefore, the accuracy of Tm affects the accuracy of the resultant PWV. Bevis et al. [3] developed the first Tm model using TS relationship. It was derived from radiosonde data at 13 U.S. sites over 2-years period and it is now the most common model with RMS error of 4.74 K. After that Bevis et al. [4] used more complex method (numerical weather prediction models NWP) to estimate Tm.Ross and Rosenfeld [15] estimated Tm by adding the parameters of geographic locations with 53 globally distributed radiosonde stations profiles and time over 23 years. After Bevis (BTm) model, many Tm models were developed such as [13], [7]. Mendes et al. [13] evaluated the accuracy of these models by using a database of mean temperature values obtained by ray-tracing. The evaluations were concluded that regionally optimized models do not provide superior performance compared to global models.

After that, Schueler et al. [16] proposed two seasonal models for Tm. Wang et al. [19] calculated Tm from a new global radiosonde dataset then evaluated it by comparing with global estimates of Tm from two currently available reanalysisdata sets.

Jade et al. [8] have validated these empirical relationships for four different geographical locations in India and showed that all the mean weighted temperature models agree. Finally the most commonly used Tm-Ts relationship is Bevis et al. [3].

There are other factors with surface temperature (Ts) such as air pressure (Ps) and water vapor (es) were used in many researches. In 2011 Wang et al. [20]compared among two models one using Ts only and another use Ts and Ps but there are no significant difference between results, and cannot achieve a high degree of accuracy on a global scale.

Yao et al. [24] used spherical harmonics, taking into account seasonal and geographic variations, and solved Tm by measuring meteorological parameters. Later on Yao et al. [25] improved accuracy than Yao et al. [24] and focus in sea areas. In (2014) Yao et al. achieved very accurate models dependent in meteorological parameters. Lan et al. [9] conclude that Tm with Ts have seasonal changes. Chen et al. [5] created several models by changing number of parameters and factor in year and seasons.

In this research, 3600 radiosonde profiles from four stations in Egypt during 2015 and 2016 and Bevis linear regression method were used to develop Tmmodel in Egypt. In addition to this the estimated Tm was used to assess the performance of the Bevis, Schueler, Yao, Liou, Suresh Raju and Wayan models.

2. Calculation of weighted mean temperature Tm

2.1. Use of a constant Tm value

The mapping scale factor Π can be used as constant value 1/6.5. This factor computed from constant Tm [2].

This means:(2) $T_{m} = 269.7 K$ where K is Kelvin.

This method is the simplest but has the lowest accuracy (eg [22]).

2.2. Use an approximate form

The value of Tm can be estimated by the parameters α (temperature lapse rate) and λ (vapor pressure decline rate) as time and location dependent [1]. The Tm model as below:(3) $T_{m} = T s (1 - \frac{α * R}{(λ - 1) * g})$ where $g$ is the acceleration gravity and R is the specific gas constant of water vapor [8.134 J/mol·K].

The parameters of Eq. (3) were difficult to obtained, and the obtained results are not accurate enough accuracy [22].

2.3. Use of local empirical formula (Bevis model)

Bevis et al. [4] investigated Tm correlation with surface temperature Ts by analyzing myriad numbers (8718) of radiosonde data in the United States. Tm is given as:(4) $T_{m} = 70.2 + 0.72 T s$ where Tm and Ts are in Kelvin. Table 1 illustrate some examples of Tm model (e.g [12]).

Table 1. Some existing Tm model (the units of Tm and Ts are Kelvin).

Tm model	Author
Tm = 0.72 Ts + 70.2.	Bevis et al. [3]
Tm = 0.64 Ts + 86.9.	Schueler et al. [16]
Tm = 0.8116 Ts + 43.69	Yao et al. [26]
Tm = 1.07 Ts- 31.	Liou et al. [11]
Tm = 0.75 Ts + 62.	Suresh Raju et al. [14]
Tm = 0.84 Ts + 48.	Wayan and Iskanda [21]

2.4. Numerical integration

The numerical integration method is also approximate computation but it is the most accurate result [6]. Tm is given as:(5) $T_{m} = \frac{\sum_{i - 1}^{n} \frac{e(i)}{T (i)} Δ h_{i}}{\sum_{i - 1}^{n} \frac{e(i)}{T^{2} (i)} Δ h_{i}}$ where i is the ith pressure level and ei, Ti and Δhi are the partial pressure (in hPa) of water vapor, atmospheric temperature (in Kelvin), and thickness (m) of the layer, respectively. Li Li et al. [10] used this expression to compute water vapor:(6) $e = 6.112 e x p (\frac{18.62 T_{S}}{243.12} + T_{S})$ where TS is in Celsius. The real data of vapor pressure are obtained from radiosonde data or numeral prediction. This expression in Eq. (6) can be used when air reaches the saturated condition, the water vapor in air will condense, and dew point temperature is the same as air temperature at this time.

3. Design of a new Tm model

3.1. Radiosonde database

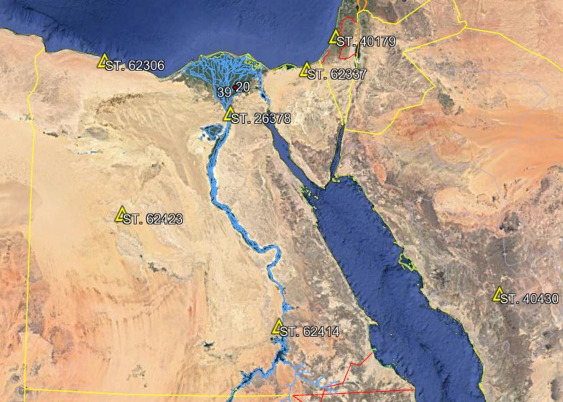
The radiosonde observation was built to measure meteorological data by using sensor to measure the pressure (Pi), temperature (Ti), dew point and geo-potential height. This observation is usually carried out by releasing a helium gas balloon into the upper atmosphere, allowing measurement of meteorological parameters. A region specific model for Tm in terms of surface temperature (Ts) was developed using the radiosonde measurements from seven radiosonde stations distributed in and around Egypt (Fig. 1). The data was obtained from the Department of atmospheric science of university of Wyoming which has a radiosonde database for the whole World. These soundings were available at http:/weather.uwyo.edu/upperair/sounding.html [17].

The data used was collected at 00:00 and 12:00UTC for all days in years 2015 and 2016. The collected data were for five stations in Egypt (Aswan, Helwan, Mersa-Matrouh, Al-Arish, and Farafra) and two stations neighboring to Egypt (Bet degan, Elmadyna) as illustrated in Table 2. These data cover a large variety of climatic conditions, where Aswan and Farafra represent southern region Helwan represents the central region, Marsa Matrouh and Arish represent the northern region of Egypt (near the Mediterranean Sea). Bet Dagan is as north latitude of Egypt and Madyna is as the south latitude of Egypt. These stations are used to test the new model.

Table 2. The codes of the stations used in this study.

Empty Cell	Code	Name	φ	λ
1	62414	Aswan	23.96	32.78
2	62378	Helwan	29.86	31.33
3	62306	Mersa-Matrouh	31.33	27.21
4	62337	Al-Arish	31.08	33.81
5	62423	Farafra	27.05	27.96
6	40179	Bet degan	32.00	34.81
7	40430	Elmadyna	24.55	39.7

3.2. Methodology of developed Tm model

The selected method to compute Tm is numerical integration method (Refer to Eq. (5)). The radiosonde data provide temperature and water vapor pressure from surface to different height. Linear regression for Tm can be derived from the radiosonde data and the surface temperature data Ts as:(7) $T_{m} = a + b T_{s}$

The values of coefficient (a, b) are obtained by the least square approach (e.g. [23]).

4. Results

4.1. Accuracy verification of Tm models

In this study, the Tm is calculated using 2 years of four well-distributed radiosonde data stations over Egypt. The calculation was done using Excel software. Fig. 2 shows the regression diagram of mean temperature (Tm) with surface temperature (Ts) at each station estimated from radiosonde stations data for the period (2015–2016).

Referring to Table 1, Although Bevis‘s model is widely used among the six models selected, But it does not represent the climate condition in Egypt. There are several global Tm models have been improved such as Schueler et al. [16]model which tries to cover the whole world using the global numerical weather prediction analysis, and Yao et al. [26] has modify the BTm model through using globally stations distributed over 10 years. To support the regional needs, BTmmodel has been adapted in most of the Tropic communities by using local or regional radiosonde observation. For example Liou’s model was developed using the radiosonde observation at Taipei spanning from year 1988 to 1997. The Suresh Raju developed a model covering the Indian region by using data from 1995 to 1997. At the same time, the Wayan‘s model was developed for Western Pacific region from 15 radiosonde stations for whole year 2011. In the present study, the performance of the above selected models which were based on different data set was assessed using four radiosonde station data sets. These stations are Aswan, Helwan, Mersa-Matrouh, and Farafra. The performance can be measured by bias and RMS by using least square method. The two statistical quantities used to measure the performance of these models are bias and RMS, which were calculated by(8) $B i a s = \frac{1}{N} \sum_{i}^{N} (T_{m}^{i} (m o d e l) - T_{m}^{i} (r e f r e n c e)) .$ (9) $R M S = \sqrt{\frac{1}{N} \sum_{i}^{N} (T_{m}^{i} (m o d e l) - T_{m}^{i} (r e f r e n c e))}$ where N is the number of the samples. Fig. 3 shows the performance of the selected models.

Fig. 3 illustrated the Tm biases for the six models using the radiosonde profiles from stations numbered (62378, 62423, 62414, and 62306) (Fig. 1). The results indicated that the biases of (Bevis, Yao, Liou, and Ragu) models were closes to each other. The results clearly demonstrate the strength of Bevis, Yao, Liou, and Ragu models where they reach to minimum biases value (3.09, 2.60, 3.20, 2.56 K) respectively in station 62423. While the models of Schular and Wayan are broken-down at all radiosonde stations.

4.2. Design Egypt Tm model

It is clear from the results of the above six models that is needed a local Tmmodel to be developed for Egypt. Development Tm model depends on the linear regression between Tm and TS analysis. The model is necessary to allow estimation of the Tm parameter without relying on the radiosonde data (Fig. 4). The result of Tm and TS statistics for the period from 2015 to 2016 appears at each station in Fig. 2 (a, b, c, and d).