Modeling technologies for desalination of brackish water

Introduction

Fresh water resources are limited and account only for 3% of the water on the Earth, of which only one third is available as liquid water [1]. Climate change, population growth, intensive agricultural use, and industrial development put pressure on these limited freshwater resources and exacerbate water scarcity issues [2]. In the US, agricultural irrigation and thermoelectric power generation were the two main users of freshwater in 2015, although agricultural use is primarily consumptive and thermoelectric power generation is largely associated with temporary withdrawals [3]. The rapid growth of unconventional oil and gas production, attributed to the development of hydraulic fracturing and horizontal drilling techniques, has also increased the associated freshwater use in most of the shale basins in the US [4,5], many of which are largely dryland areas. Drylands that contain arid, semi-arid, and dry subhumid regions cover about 40% of the Earth’s land surface and more than 2 million km2 of the land area in the US [6]. The large quantities of freshwater use by agriculture, thermoelectric power, and oil and gas explorations in the arid and semi-arid areas of the western US can intensify local water shortages [4,7•,8,9].

Often the quality of the water used in hydraulic fracturing and other non-potable uses is higher than what is needed [2]. Thus, exploring alternative water resources with lower quality to support a ‘fit-for-purpose’ water use model can help conserve freshwater. Enabling brackish water for irrigation, for example, could dramatically ease demands for high-quality freshwater and aid in the economic development of agricultural regions such as Southern High Plains of Texas [7•]. In addition, poor-quality brackish waters could be upgraded for high quality potable water needs if treatment technologies are effective and efficient.

Brackish water is a saline water with total dissolved solids (TDS) less than that of seawater. The US geological survey (USGS) has defined a TDS level between 1000–10 000 mg/L for brackish ground water in the US and categorized these waters according to their chemical compositions into four main groups. The first three groups include water types with sodium-bicarbonate, calcium-sulfate, and sodium-chloride as major components while the last group includes water containing a low concentration of a variety of cations and anions [10•]. In some cases, brackish water can be used directly or after diluting with freshwater for hydraulic fracturing, power plants, and irrigation of high salt-tolerant crops [7•,9,11]. However, the existence of minerals with concentrations above their solubilities increases salt precipitation and scaling issues. Thermodynamic analyses of phase equilibria in these saline waters help evaluate scaling, which can be used to assess potential uses or salinity management techniques [12,13•,14•]. Total or partial desalination of brackish water to remove scale-precipitating components or reduce TDS to manageable levels can make these alternative water resources suitable for industrial, agricultural, and municipal uses. The choice of desalination technique depends on many factors including the chemistry of feed water, final use of treated water, and energy consumption of the desalination process [15]. Desalination techniques can be categorized as thermal, chemical, membrane, electro-membrane, and electrochemical processes [16, 17, 18].

Widely used thermal desalinations technologies include multi-stage flash (MSF) and vapor compression (VC). The thermal processes are energy-intensive and are most suitable for areas with low energy costs such as the Middle East [19]. Ion exchange and solvent extraction are among the chemical desalination processes which can be used for removal of ions from saline waters but their efficiency is sufficiently high only at low ionic concentrations [20,21]. Membrane techniques include microfiltration (MF), ultrafiltration (UF), nanofiltration (NF), and reverse osmosis (RO). These are pressure driven processes to remove particles, bacteria, and salts from water via size exclusion through membranes with different pore sizes [16]. RO is a widely used technique due to its relatively low energy consumption compared to thermal processes. The technology is mature and accounts for ∼65% of the installed desalination capacity in the world [22]. However, high-pressure operations and the sensitivity of membranes to the quality of feed water increase both capital and operational costs. These challenges encourage the exploration of electro-membrane and electrochemical desalination techniques for brackish water [18]. In electro-membrane technologies such as electrodialysis (ED) and electrodialysis reversal (EDR), ion exchange membranes (IEMs) are used. IEMs pass counterions (ions with opposite charge to that of the fixed charge groups of the membranes) but block co-ions (ions with the same charge to that of fixed charge groups of the membranes). In ED(R), an electric field provides the driving force for selective transport of ions through IEMs and desalinating water [16]. Capacitive deionization (CDI) is an emerging electrochemical process which involves the adsorption of ions into porous electrodes under an electrostatic field and has the potential advantage of eliminating the need for membranes and the associated pretreatment steps [23,24]. CDI can also be used with IEMs to improve adsorption capacity although with the disadvantage of potential increasing pretreatment requirements.

This review focuses on ED, CDI, and membrane CDI (MCDI) processes and modeling approaches for their optimization and design. The review discusses the unique attributes of these techniques that may make them reliable options for brackish water desalination.

ED process

ED is a low-pressure electro-membrane technique and relative to RO, requires small energy input for desalination of low salinity brackish water [19,25]. Optimizing the operating conditions of ED can significantly improve the energy consumption of the system, especially for desalination of feed water with higher salinity [26]. Compared to RO, membranes used in ED have higher chemical and mechanical stability and can sustain higher temperatures [27,28]. Hence, less pretreatment and additive chemicals are required for ED. The plate and frame configuration of ED means the membrane treatments can be implemented relatively simply compared to the spiral wound configuration of RO. In general, less biofouling and mineral scaling occur on membranes and they can further be controlled by switching to reverse mode. The quality of the desalinated water can be adjusted by changing imposed electrical potential, enabling ED for partial desalination of saline water. Because of the electrical nature of the process, ED is also capable of selective removal of ions, for example, divalent ions which are often the source of precipitation and scale.

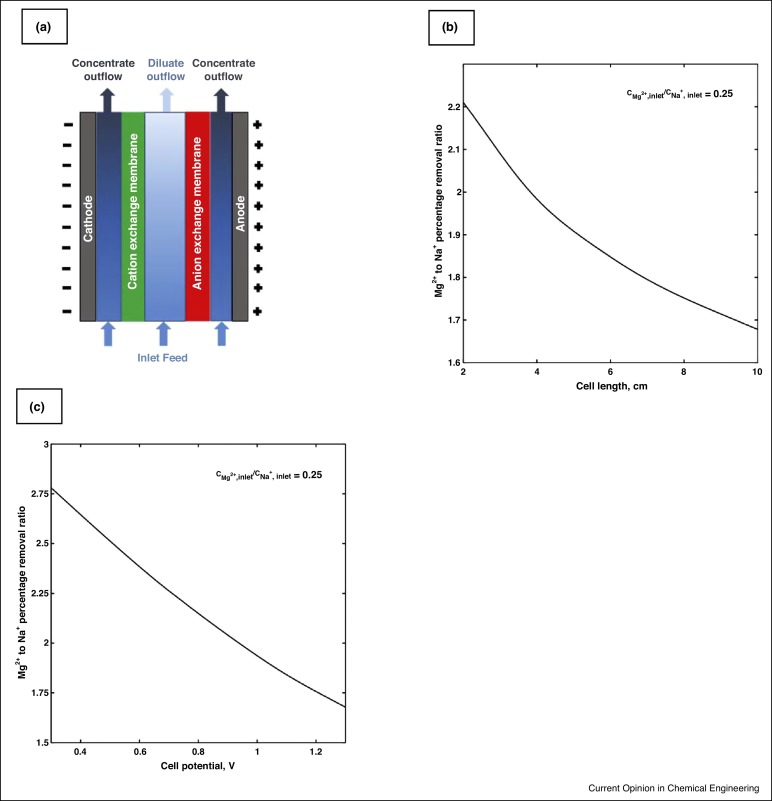
The separation efficiency in ED relies on cell design, system hydrodynamics, membrane properties, and operating conditions. We develop a 2D ion transport model for ED with the aim of identifying and optimizing the effective parameters for ion removal. The ionic fluxes are described using the Nernst-Planck (NP) equation with Teorell’s diffusion for high concentration and with Fick’s diffusion for dilute solutions [29, 30, 31]. To investigate the hydrodynamic effects, both spacer-free and spacer-filled cells are modeled and the laminar flow Navier-Stokes (NS) equations are solved to identify the velocity profiles. No-slip boundary conditions are assumed on surfaces of IEMs and spacer filaments [32]. Figure 1a represents a schematic of the spacer-free cell. The non-ideal solution effects caused by higher ionic concentrations are modeled using the polyelectrolyte nonrandom two-liquid (polyelectrolyte NRTL) activity coefficient model [33]. Substituting the NP equation in molar balance equation at the steady-state (st-st) condition results in a set of N equations and N + 1 unknowns including the concentration of N species and potential distribution in the cell. The equations can be solved with the additional constraint of electroneutrality. Local electrochemical equilibrium known as Donnan equilibrium is applied at IEMs-solution interfaces causing step changes in concentrations and potential in these regions [34]. The developed model accounts for co-ion transport through membranes and relaxes the ideal membrane assumptions applied in prior modeling efforts [35,36]. The experimentally measured current density versus electrical potential curves in ED show a low voltage region with a linear increase in current with potential (known as ohmic regime) followed by a plateau (known as limiting current density), and end with a linear increase at high potential (known as overlimiting current density). Our model is applicable to ED operated in the ohmic regime.

The 2D ion transport model is capable of qualitatively describing the concentration and potential distributions in both spacer-free and spacer-filled cells. The modeling results for an aqueous NaCl solution showed that the impacts of the solution non-ideality are minor for the salinity range of brackish water. Using spacers in channels results in higher limiting current densities than the current obtained in the spacer-free cell. This increase in current density is attributed to the enhanced cross-channel mixing in the spacer-filled cell. The model has been employed for an aqueous Na+-Mg2+-Ba2+-SO42−-Cl−quinary solution to evaluate the ability to selectively remove scale precipitating ions. The results indicate that cell length, imposed electrical potential, the use of spacers, the ion concentrations and total ionic strength in the feed solution, and membrane properties affect the selective removal of ions in the cell. Increases in divalent ion concentrations and Donnan potential drops at the IEMs-solution interfaces benefit selective removal of divalent to monovalent ions in the cell. Increases in the cell length and imposed electrical potential decrease the selective Mg2+ to Na+ removal in the diluate channel of the spacer-free cell as demonstrated in Figure 1b and c, respectively.

To minimize the required membrane surface, ED units are preferred to be operated at high electrical potential, increasing the possibility of reaching limiting and overlimiting current regimes. Thus, the model needs to be extended to account for the phenomena taking place in these high current regimes including water splitting, gravitational convection, and electro-convection [37••,38]. Such effort involves replacing electroneutrality by Poisson equation due to increases in thicknesses of space charge regions, correcting the NS equations to account for electrostatic body forces, accounting for water dissociation reactions, and considering solution density changes.

The developed model can be employed to characterize performance of an ED cell operated in the ohmic regime and for designing experiments to optimize the cell performance. However, for meaningful comparison of the modeling results with experimental data, the model framework should be improved to describe the flow behavior in 3D, take into account the effects of spacer geometry, consider biofouling and mineral fouling on the membranes and spacers, account for water transport through the membranes, and be expanded to more and different membrane types.

(M)CDI process

CDI is a competitive technology for desalination of low salinity brackish water due to the low input potential and low-pressure operating conditions required [39,40]. CDI is a membrane-less technique and thus does not require pre-treatment to prevent membrane fouling. The salinity of CDI effluent can be tuned by changing operation conditions, allowing fit-for-purpose desalination [41]. Similar to ED, the inorganic and organic fouling can be controlled by switching the polarity of the electrodes and using pulsed field in CDI. In general, less fouling and scaling issues are observed for CDI compared to membrane techniques such as RO [42,43]. CDI can also provide selective removal of ions based on the ionic charge and hydrated radius [44,45].

MCDI contains IEMs between spacers and electrodes to allow easy access of counterions and prevent the penetration of the co-ions, improving the salt removal ratio of the cell. In MCDI, selective ion removal can be achieved by tailoring the membrane properties [46,47]. The use of IEMs in MCDI cell decreases the extent of Faradaic reactions occurring in the cell and improves the charge efficiency of the process [48, 49, 50]. However, the high cost of ion exchange membranes [51] increases the capital and maintenance costs of MCDI compared to CDI.

CDI and MCDI are emerging technologies and there are limitations on successful coupling of the electrode pairs into stacks, and stacks into modules, to scale up the process. Enhancing the long-term stability of the electrodes without increasing the total cost is another challenge for both techniques [52]. The energy demand of the (M)CDI processes have been compared with RO and several studies have demonstrated lower energy consumption for desalination of low salinity brackish water with (M)CDI [53,54,55]. However, comparing the energy consumption of a lab-scale (M)CDI and a large-scale RO may not provide a valid conclusion due to the more comprehensive energy needs in a full-scale system [56•].

Here we use a model to compare CDI and MCDI performance. (M)CDI is described with a fully coupled 2D model for ion transport and adsorption behavior in the cell during charging. For both CDI and MCDI cells, the electrodes are modeled as a series of macropores through which ions are transported to the collection surface present in micropores. Chemically modified electrodes have been investigated in the literature and are shown to improve the ion removal in (M)CDI cells [57,58]. However, the focus of the current effort is modeling commercially available carbon cloth electrodes. The ionic fluxes in channel and in electrode macropores are described using the NP equation. The ion adsorption in electrode micropores is described using the Nernst equation. The Darcy’s law is employed to calculate the flow velocity in the spacer-filled channel treated as a saturated porous media [32]. In MCDI, the NP equation is used to calculate the ionic fluxes in non-ideal IEMs accounting for co-ion transport through membranes as well. Donnan equilibrium is applied at the IEMs-solution interfaces.

Figure 2a illustrates a half CDI cell containing a half of spacer-filled channel and an electrode. Because of electroneutrality, the concentration distribution in both half-cells of a CDI cell are identical. Figure 2b shows the change of ion concentration in the effluent of the half-cell from 50 to 3000 s with an influent concentration of 20 mol/m3. Initially, the electrode experiences a high adsorption rate in the micropores of electrodes, resulting in a rapid decrease in ion concentration. As micropores become increasingly saturated, the effluent concentration asymptotically increases back to the influent concentration of 20 mol/m3. As shown in Figure 2c, increases in the imposed potential slows the rate of system equilibration. The use of MCDI increases the rate of desalination and increases salt removal efficiency relative to CDI. The model describes 2D concentration and potential distributions inside the cell, which can neither be measured in the lab, nor have they been simulated well by prior models [59,60,61•]. The overall energy efficiency of the system is a strong function of the quality of the effluent water and the degree of saturation achieved in the electrodes. The model can be used to optimize the energy efficiency, which is often achieved by cycling the system more rapidly rather than allowing the electrodes achieve near saturation.

The modeling framework needs to be extended to multicomponent solutions to analyze selective ion removal. Adjustments are also necessary to expand the modeling framework to account for Faradaic reactions and effects of pore size distribution in the electrodes.

The developed model can qualitatively represent the experimental data measured for (M)CDI cells and can be used to identify the critical parameters affecting the performance of the cells. However, the simplifying assumptions used in the modeling framework and the lack of key characteristics associated with the membranes and electrodes make the exact prediction of experimental data challenging.

Conclusion

Meeting future demands for water requires the exploitation of non-traditional sources of water. The relatively low salinity of brackish groundwater makes desalination feasible but better process design and optimization is required to fully utilize available technologies. ED and (M)CDI have the potential to reduce the cost of desalination by simplifying pretreatment and promoting selective ion removal.

A 2D ion transport model suggest that the non-ideal solution impacts on ion transport in ED are minor. However, hydrodynamics plays a significant role and using spacers in the channel increases the limiting current density values in the cell. The model is used to investigate the effective parameters for selective divalent ion removal. The results indicate that decreasing the cell length and cell potential enhances the selectivity toward divalent ions. The developed modeling framework is limited to an ED cell operated in the ohmic regime and further improvements are required to expand the model for limiting and overlimiting current transfer.

A 2D transient model with coupled transport and adsorption is developed for a spacer-filled (M)CDI cell and used to estimate concentration and potential distributions in the cell. The model can be used to investigate the adsorption and transport phenomena in the cell and adjust the operating conditions to achieve optimal desalination performance. Comparing MCDI and CDI indicates that using IEMs in the MCDI improves the ion removal ratio compared to the membrane-less CDI cell at the cost of potential requiring greater water pretreatment. The current model does not account for Faradaic reactions and pore size distribution effects in electrodes. The model does not currently simulate multicomponent solutions and ion selectivity.